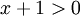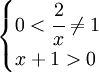Ôn tập Tốt nghiệp THPT 2009-2010/Hàm số, phương trình, bất phương trình mũ và lôgarit
Nội dung hàm số, phương trình, bất phương trình mũ và logarit trong cấu trúc đề thi:
Phần chung: Hàm số, phương trình, bất phương trình mũ và lôgarit.
Phần riêng của CTNC: Hệ phương trình mũ và lôgarit.
Mũ[sửa]
Lý thuyết[sửa]
+ Các phép toán trên hai lũy thừa cùng cơ số, hai lũy thừa cùng số mũ.
+ Quy tắc so sánh hai lũy thừa cùng cơ số (Trong hai lũy thừa cùng cơ số lớn hơn 1, lũy thừa nào có số mũ lớn hơn thì lũy thừa đó lớn hơn và ngược lại. Nói tắt: "Cơ số lớn hơn 1, cùng chiều. Cơ số nhỏ hơn 1, ngược chiều")
+
Hàm
số
mũ
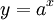 (0
<
a
≠
1)
(0
<
a
≠
1)
- Tập xác định: ℝ
- Tập giá trị: (0; +∞)
-
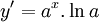
- 0 < a < 1 ⇒ y' < 0 ⇒ hàm số nghịch biến
- a > 1 ⇒ y' > 0 ⇒ hàm số đồng biến
- Đồ thị hàm số luôn nằm trên trục hoành và đi qua điểm B(0; 1)
+ Các phương pháp giải phương trình, bất phương trình mũ
- Đưa về cùng cơ số
- Đặt ẩn phụ
- Logarit hóa
Ví dụ[sửa]
Giải các phương trình, bất phương trình sau:
a)
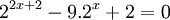
b)
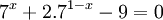
c)
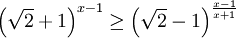
Bài tập tự luyện[sửa]
Giải
phương
trình
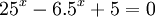 .
.
Giải
phương
trình
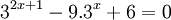 .
.
Giải
phương
trình
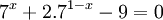 .
.
Giải
phương
trình
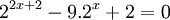 .
.
Logarit[sửa]
Lý thuyết[sửa]
+ Các phép toán trên hai logarit cùng cơ số.
+ Các công thức đổi cơ số.
+
Quy
tắc
xét
dấu
logarit.
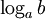 >
0
<=>
a
và
b
cùng
lớn
hơn
hoặc
cùng
nhỏ
hơn
1.
>
0
<=>
a
và
b
cùng
lớn
hơn
hoặc
cùng
nhỏ
hơn
1.
+ Quy tắc so sánh hai logarit cùng cơ số. Cơ số lớn hơn 1, cùng chiều. Cơ số nhỏ hơn 1, ngược chiều.
+
Hàm
số
logarit
y
=
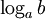 (0
<
a
≠
1)
(0
<
a
≠
1)
- Tập xác định: (0; +∞)
- Tập giá trị: R
-
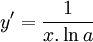
- 0 < a < 1 ⇒ hàm số nghịch biến
- a > 1 ⇒ hàm số đồng biến
- Đồ thị hàm số luôn nằm bên phải trục tung và đi qua A(1; 0).
+ Các phương pháp giải phương trình, bất phương trình logarit
- Đưa về cùng cơ số
- Đặt ẩn phụ
- Mũ hóa.
Ví dụ[sửa]
Giải các phương trình, bất phương trình sau:
a)
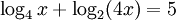
b)
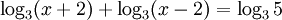
c)
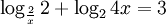
d)
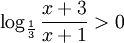
Bài tập tự luyện[sửa]
Giải
phương
trình
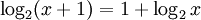 .
.
Giải
phương
trình
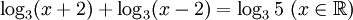 .
.
Giải
phương
trình
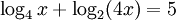 .
.
Sai lầm và cách sửa[sửa]
| Sai | Đúng |
|---|---|
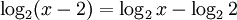 |
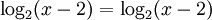 -:D
-:D |
Phương
trình
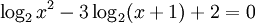
|
Phương
trình
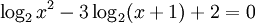
|
|
Điều
kiện
của
phương
trình
|
Điều
kiện
của
phương
trình
|
Chủ đề khác[sửa]
- Khảo sát hàm số và các bài toán liên quan
- Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Hàm số, phương trình, bất phương trình mũ và lôgarit
- Hình học không gian tổng hợp
- Phương pháp tọa độ trong không gian
- Nguyên hàm, tích phân, ứng dụng
- Số phức
<comments
/>
Bài liên quan
Liên kết đến đây
- Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan
- Bản mẫu:Ôn tập Tốt nghiệp THPT 2009-2010
- Ôn tập Tốt nghiệp THPT 2009-2010/Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
- Ôn tập Tốt nghiệp THPT 2009-2010/Hình học không gian tổng hợp
- Ôn tập Tốt nghiệp THPT 2009-2010/Phương pháp tọa độ trong không gian
- Ôn tập Tốt nghiệp THPT 2009-2010/Nguyên hàm, tích phân, ứng dụng
- Ôn tập Tốt nghiệp THPT 2009-2010/Số phức
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/1
- Ôn tập Tốt nghiệp THPT 2009-2010/Khảo sát hàm số và các bài toán liên quan/2
- Xem thêm liên kết đến trang này.
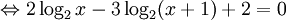
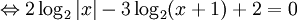
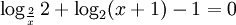 là
là