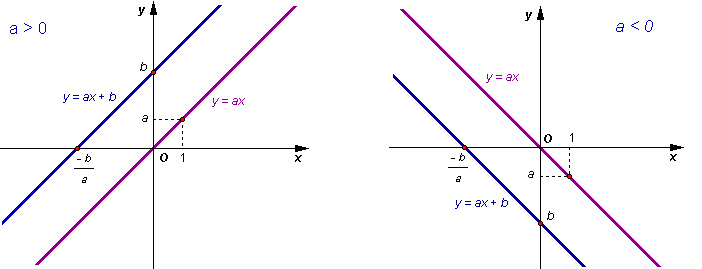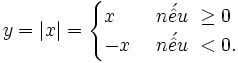Đại số 10/Chương II/§2. Hàm số y = ax - b

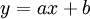Trong mặt phẳng tọa độ, đồ thị của hàm số bậc nhất $y=ax+b$ (a ≠ 0) là một đường thẳng.
Ngược lại, điều đó còn đúng không: Mỗi đường thẳng đều là đồ thị của một hàm số bậc nhất nào đó?

Lí thuyết

Cho hàm số y = ax + b, trong đó x là biến số, a và b là các hằng số.

• Nếu a ≠ 0, thì hàm số y = ax + b chính là hàm số bậc nhất mà ta đã biết.
• Nếu a = 0, thì hàm số y = ax + b trở thành y = b - và nó được gọi là hàm số hằng mà ta sẽ tìm hiểu dưới đây.

Ôn tập về hàm số bậc nhất

Phương trình: y = ax + b (a ≠ 0)

Tập xác định: D = R.

Chiều biến thiên

Với a > 0 hàm số đồng biến trên R.

Với a < 0 hàm số nghịch biến trên R.

Đồ thị

Hình 17

Đồ thị của hàm số bậc nhất là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn song song với đường thẳng y = ax (nếu b ≠ 0) và đi qua hai điểm A(0;b); B(-b/a;0) (hình 17).

Hoạt động 1	Vẽ đồ thị của các hàm số: y = 3x + 2; $y=-{\frac {1}{2}}x+5\$ .

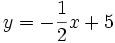Ngược lại, người ta chứng minh được rằng: mọi đường thẳng nằm trong mặt phẳng tọa độ mà không song song và không trùng các trục tọa độ đều là đồ thị của một hàm số bậc nhất nào đó, tức là đều có phương trình dạng y = ax + b (a ≠ 0).

Từ đó, một vấn đề đặt ra là: Những đường thẳng song song hoặc trùng với các trục tọa độ thì có phương trình như thế nào?

Dễ thấy rằng, các đường thẳng này gồm hai loại:

• Loại 1: Gồm các đường thẳng song song hoặc trùng với trục hoành.
• Loại 2: Gồm các đường thẳng song song hoặc trùng với trục tung.

Việc phân chia như thế, sẽ giúp chúng ta dễ dàng tìm được phương trình của chúng.

Hàm số hằng y = b

Như trên, ta đã biết: hàm số hằng y = b là trường hợp đặc biệt của hàm số y = ax + b khi a = 0. Hàm số y = b có tập xác định R, không đồng biến và cũng không nghịch biến trên tập xác định của nó.

Hoạt động 2	Cho hàm số hằng y = 2. Xác định giá trị của hàm số tại x = -2; -1; 0; 1; 2. Biểu diễn các điểm (-2;2), (-1;2), (0;2), (1;2), (2;2) trên mặt phẳng tọa độ. Nêu nhận xét về đồ thị của hàm số y = 2.

	Hình 18 Đồ thị của hàm số y = b là một đường thẳng: song song với trục hoành và cắt trục tung tại điểm (0;b), nếu b ≠ 0. trùng với trục hoành, nếu b = 0. Đường thẳng này gọi là đường thẳng y = b (hình 18).

Đường thẳng x = c

Tập tin:Duong thang x = c

Đường thẳng x = c.

Trong mặt phẳng tọa độ, xét đường thẳng (Δ) song song với trục tung và cắt trục hoành tại điểm C(c; 0) với c ≠ 0 (hình vẽ).

Dễ thấy, mọi điểm thuộc đường thẳng (Δ) đều có hoành độ x = c và ngược lại mọi điểm có hoành độ là c đều thuộc đường thẳng (Δ).

Đặc biệt, khi c = 0 thì điểm C(c; 0) trùng với gốc tọa độ O(c; 0) và đường thẳng (Δ) trùng với trục tung Oy.

Từ đó có thể viết rằng, mọi đường thẳng (Δ) song song với trục tung hoặc trùng với trục tung đều có phương trình là x = c.

Đường thẳng ax + by + c = 0

Tổng hợp các kết quả trên, ta có thể viết:

Phương trình đường thẳng (Δ):

• không song song và không trùng với các trục tọa độ có dạng: y = ax + b, (a ≠ 0).
• song song hoặc trùng với trục hoành có dạng: y = b.
• song song hoặc trùng với trục tung có dạng: x = c.

Trường hợp tổng quát, người ta chứng minh được rằng:

Mọi đường thẳng trong mặt phẳng tọa độ đều có phương trình dạng: Ax + By + C = 0 trong đó A, B, C là các hằng số (A và B không đồng thời bằng 0).

Hàm số y = |x|

Hàm số y = |x| có liên quan chặt chẽ với hàm số bậc nhất.

Tập xác định

Hàm số y = |x| xác định với mọi x, tức là tập xác định D = R.

Chiều biến thiên

Theo định nghĩa của giá trị tuyệt đối, ta có:

$y=|x|={\begin{cases}x\ &n{\acute {{\hat {e}}}}u\ \geq 0\\-x\ &n{\acute {{\hat {e}}}}u\ <0.\end{cases}}\$

Từ đó suy ra

	Hàm số y = |x| nghịch biến trên khoảng (-∞;0) và đồng biến trên khoảng (0;+∞).

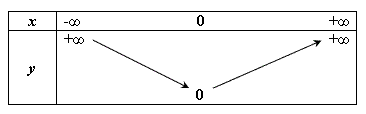
Bảng biến thiên

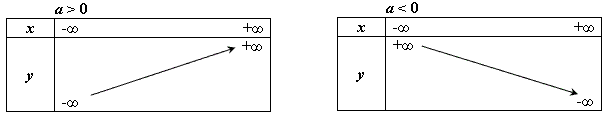
Khi x > 0 và dần tới +∞ thì y = x dần tới +∞; khi x < 0 và dần tới -∞ thì y = -x cũng dần tới +∞. Ta có bảng biến thiên sau:

Hình 19

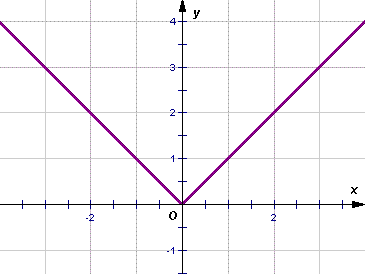
Đồ thị

• Trong nửa khoảng [0;+∞) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = x.
• Trong khoảng (-∞;0) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = -x.

CHÚ Ý

Hàm số y = |x| làm một hàm số chẵn, đồ thị của nó nhận Oy làm trục đối xứng.

BÀI TẬP

1. Vẽ đồ thị của hàm số

a) y = 2x - 3;	b) $y={\sqrt {2}}\$
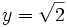
c) 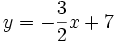$y=-{\frac {3}{2}}x+7$ ;	d) y = |x| - 1.

2. Xác định a, b để đồ thị của hàm số y = ax + b đi qua các điểm

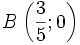
a) A(0;3) và $B\left({\frac {3}{5}};0\right)\$	b) A(1;2) và B(2;1)
c) A(15;-3) và B(21;-3)	d)

3. Viết phương trình y = ax + b của các đường thẳng

a) Đi qua hai điểm A(4;3) và B(2;-1);

b) Đi qua điểm A(1;-1) và song song với Ox.

4. Vẽ đồ thị các hàm số

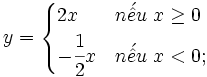
a) $y={\begin{cases}2x&n{\acute {{\hat {e}}}}u\ x\geq 0\\-{\cfrac {1}{2}}x&n{\acute {{\hat {e}}}}u\ x<0;\end{cases}}$

b) $y={\begin{cases}x+1&n{\acute {{\hat {e}}}}u\ x\geq 1\\-2x+4&n{\acute {{\hat {e}}}}u\ x<1.\end{cases}}$

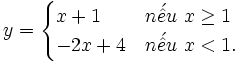
Tài liệu tham khảo

• Đại số 10, Nhà xuất bản Giáo dục, 2006, trang 39.
• Đại số 10 Nâng cao, Nhà xuất bản Giáo dục, 2006, trang 48.
• Đại số 10, Nhà xuất bản Giáo dục, 2001, trang 30.
• Tài liệu giáo khoa thí điểm, Đại số 10, Ban khoa học tự nhiên, Nhà xuất bản Giáo dục, 1997, trang 39, 42.

Xem thêm

• Đại số 9/Chương II/§2. Hàm số bậc nhất
• wikibooks:Algebra/Function_graphing
• wikibooks:Algebra/Systems_of_simultaneous_equations
• en:Linear function

---

<<< Đại số 10

Liên kết đến đây

• Đại số 10
• Thành viên:Nguyenthephuc/Note: Đang viết
• Đại số 9/Chương II/§2. Hàm số bậc nhất
• Đại số 9/Chương II/§3. Đồ thị của hàm số y = ax - b (a ≠ 0)
• Phân phối chương trình môn Toán lớp 10, Trung học phổ thông, Năm học 2006 - 2007
• Đại số 10/Chương IV/§4. Bất phương trình bậc nhất hai ẩn