Đại số 10/Chương IV/§3. Dấu của nhị thức bậc nhất/Giáo án
Mục lục
- 1 MỤC TIÊU
- 2 CHUẨN BỊ PHƯƠNG TIỆN DẠY HỌC
- 3 GỢI Ý VỀ PPDH
-
4
TIẾN
TRÌNH
BÀI
HỌC
VÀ
CÁC
HOẠT
ĐỘNG
- 4.1 Các tình huống học tập
-
4.2
Tiến
trình
bài
học
- 4.2.1 KIỂM TRA BÀI CŨ
-
4.2.2
BÀI
MỚI
- 4.2.2.1 Hoạt động 2: Dẫn đến định lí
- 4.2.2.2 Hoạt động 3: Phát biểu định lí
- 4.2.2.3 Hoạt động 4: Chứng minh định lí
- 4.2.2.4 Hoạt động 5: Rèn luyện kĩ năng
- 4.2.2.5 Hoạt động 6: Củng cố định lí thông qua bài tập phức tạp
- 4.2.2.6 Hoạt động 7: Củng cố định lí
- 4.2.2.7 Hoạt động 8: Củng cố định lí
- 4.2.2.8 Hoạt động 9: Củng cố định lí
- 4.2.3 CỦNG CỐ TOÀN BÀI
- 4.2.4 BÀI TẬP VỀ NHÀ
- 5 Tài liệu tham khảo
- 6 Xem thêm
- 7 Liên kết ngoài
MỤC TIÊU[sửa]
Kiến thức
- Khái niệm nhị thức bậc nhất, định lí về dấu của nhị thức bậc nhất.
- Cách xét dấu tích, thương các nhị thức bậc nhất.
- Cách bỏ giá trị tuyệt đối trong biểu thức có chứa giá trị tuyệt đối của những nhị thức bậc nhất.
Kĩ năng
- Thành thạo các bước xét dấu nhị thức bậc nhất.
- Hiểu và vận dụng được các bước lập bảng xét dấu.
- Biết cách giải bất phương trình dạng tích, thương, hoặc có chứa giá trị tuyệt đối của những nhị thức bậc nhất.
Tư duy
- Hiểu được cách chứng minh định lí về dấu của nhị thức bậc nhất.
- Biết quy lạ về quen.
Thái độ
- Cẩn thận, chính xác.
- Bước đầu hiểu được ứng dụng của định lí về dấu của nhị thức bậc nhất.
CHUẨN BỊ PHƯƠNG TIỆN DẠY HỌC[sửa]
Thực tiễn
- Học sinh đã học cách giải phương trình bậc hai một ẩn ở lớp 9, giải phương trình với hệ số bằng số.
- Học sinh đã học đồ thị hàm số y = ax + b.
Phương tiện
- Chuẩn bị các bảng kết quả mỗi hoạt động (để treo hoặc chiếu qua overhead hay dùng projector).
- Chuẩn bị các phiếu học tập hoặc hướng dẫn hoạt động.
GỢI Ý VỀ PPDH[sửa]
Cơ bản dùng PP gợi mở, vấn đáp thông qua các hoạt động điều khiển tư duy, đan xen hoạt động nhóm.
TIẾN TRÌNH BÀI HỌC VÀ CÁC HOẠT ĐỘNG[sửa]
Các tình huống học tập[sửa]
Tình huống 1
Giáo viên nêu vấn đề bằng bài tập. Giải quyết vấn đề thông qua 6 hoạt động:
- Hoạt động 1: Giải bất phương trình bậc nhất, nhằm kiểm tra kiến thức cũ.
- Hoạt động 2: Xét dấu nhị thức bậc nhất với hệ số bằng số, nhằm dẫn vào định lí.
- Hoạt động 3: Phát biểu định lí (SGK).
- Hoạt động 4: Chứng minh định lí.
- Hoạt động 5: Rèn luyện kĩ năng thông qua bài tập có tham số.
- Hoạt động 6: Xét dấu của tích, từ đó giúp học sinh biết cách giải bất phương trình chứa tích các nhị thức bậc nhất.
Tình huống 2
Giáo viên nêu vấn đề bằng bài tập. Giải quyết vấn đề qua 2 hoạt động:
- Hoạt động 7: Xét dấu của biểu thức có chứa giá trị tuyệt đối của các nhị thức bậc nhất.
- Hoạt động 8: Giải bất phương trình chứa giá trị tuyệt đối của các nhị thức bậc nhất.
Tiến trình bài học[sửa]
KIỂM TRA BÀI CŨ[sửa]
Hoạt động 1: Giải các bất phương trình bậc nhất[sửa]
Giải các bất phương trình sau:
- a) 2x - 3 > 0.
- b) -3x + 7 > 0.
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
|
Giải các bất phương trình như đã học ở bài trước. |
|
BÀI MỚI[sửa]
Hoạt động 2: Dẫn đến định lí[sửa]
Xét dấu của f(x) = 2x - 6.
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
|
|
Hoạt động 3: Phát biểu định lí[sửa]
Phát biểu định lí như SGK.
Hoạt động 4: Chứng minh định lí[sửa]
Chứng minh định lí về dấu của f(x) = ax + b với a ≠ 0.
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
|
|
Hoạt động 5: Rèn luyện kĩ năng[sửa]
Xét dấu của f(x) = mx - 1 với m ≠ 0.
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
|
|
Hoạt động 6: Củng cố định lí thông qua bài tập phức tạp[sửa]
Xét
dấu
của
biểu
thức
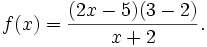
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
|
|
Hoạt động 7: Củng cố định lí[sửa]
Củng cố định lí thông qua việc giải phương trình có chứa giá trị tuyệt đối của nhị thức bậc nhất.
Giải
phương
trình:
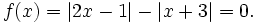 (*)
(*)
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
|
|
Hoạt động 8: Củng cố định lí[sửa]
Củng cố định lí thông qua việc giải bất phương trình có chứa giá trị tuyệt đối của nhị thức bậc nhất.
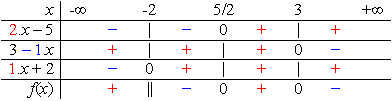
Giải bất phương trình: |-2x + 1| - |x + 3| < 2. (1*)
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
Tập nghiệm của bất phương trình (1*) là: |
|
Hoạt động 9: Củng cố định lí[sửa]
Củng
cố
kiến
thức
thông
qua
giải
bất
phương
trình
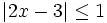 .
.
| Hoạt động của học sinh | Hoạt động của giáo viên |
|---|---|
|
Cách
1:
Vậy tập nghiệm của bất phương trình là [1;2]. Cách 2:
Vậy tập nghiệm của bất phương trình là hợp của hai tập: |
Giao bài tập và hướng dẫn học sinh cách giải. Cách 1
Cách 2
Lưu ý: Nghiệm của bất phương trình là hợp của các tập nghiệm của các hệ bất phương trình. |
CỦNG CỐ TOÀN BÀI[sửa]
Câu hỏi 1:
- a) Phát biểu định lí về dấu của nhị thức bậc nhất.
- b) Nêu các bước xét dấu một tích hoặc thương những nhị thức bậc nhất.
- c) Nêu cách giải bất phương trình có chứa giá trị tuyệt đối của những nhị thức bậc nhất.
Câu hỏi 2: Chọn phương án đúng:
Bất
phương
trình
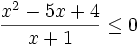 có
tập
nghiệm
là:
có
tập
nghiệm
là:
| A) Tập rỗng |
B)
(-1;1)
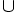 [4;+∞)
[4;+∞) |
C)
(-∞;-1]
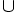 [1;4]
[1;4] |
D)
(-∞;-1)
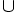 [1;4]
[1;4] |
BÀI TẬP VỀ NHÀ[sửa]
Các bài 1, 2, 3 trong SGK.
Tài liệu tham khảo[sửa]
- Sách in: Tài liệu bồi dưỡng giáo viên thực hiện chương trình, sách giáo khoa lớp 10 Trung học phổ thông, môn Toán học; Nhà xuất bản Giáo dục, 2006, trang 114.



 2x
-
6
=
0
2x
-
6
=
0
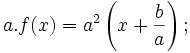 a
≠
0.
a
≠
0.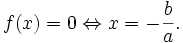
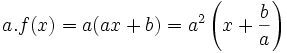
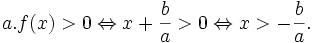
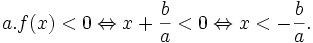
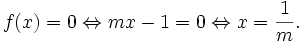
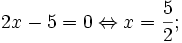 3
-
x
=
0
3
-
x
=
0
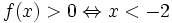 hoặc
hoặc
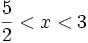
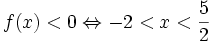 hoặc
hoặc
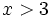
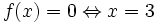 hoặc
hoặc
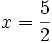
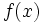 không
xác
định
khi
không
xác
định
khi
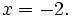
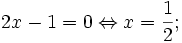
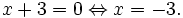
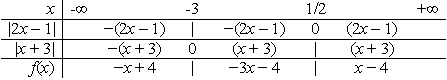
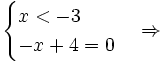 phương
trình
(*)
vô
nghiệm
phương
trình
(*)
vô
nghiệm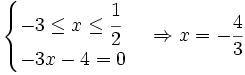
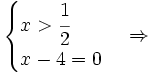 phương
trình
(*)
vô
nghiệm
phương
trình
(*)
vô
nghiệm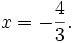
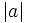
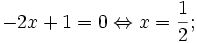
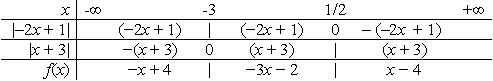
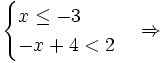 hệ
bất
phương
trình
vô
nghiệm.
hệ
bất
phương
trình
vô
nghiệm.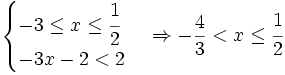
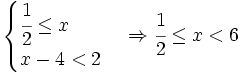
![T=\left(-{\frac 43};{\frac 12}\right]\cup \left[{\frac 12};6\right)=\left(-{\frac 43};6\right).](https://tusach.thuvienkhoahoc.com/images/math/5/b/7/5b7dfb00c6a6056087b96039a45364be.png)
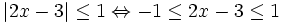
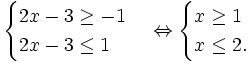
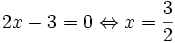
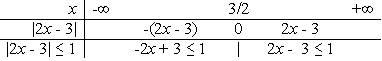
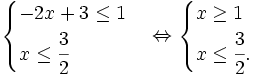
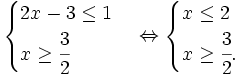
![\left[1;{\frac 32}\right]\cup \left[{\frac 32};2\right]=[1;2].](https://tusach.thuvienkhoahoc.com/images/math/5/7/b/57b6121682e22ee631afa4cc6f966771.png)
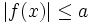 hoặc
hoặc
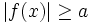 với
a
>
0.
với
a
>
0.
