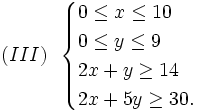Đại số 10/Chương IV/§4. Bất phương trình bậc nhất hai ẩn

Miền nghiệm của bất phương trình bậc nhất hai ẩn là gì?

Một bất phương trình bậc nhất có thể chứa một ẩn số, hoặc nhiều hơn. Chẳng hạn:

2x + y³ - z;       3x + 2y < 1.

là hai bất phương trình bậc nhất lần lượt chứa ba ẩn số, hai ẩn số. Chúng được gọi chung là bất phương trình bậc nhất chứa nhiều ẩn số. Trong bài này, chúng ta sẽ tìm hiểu chi tiết về các bất phương trình thuộc loại thứ hai.

Lí thuyết

Bất phương trình bậc nhất hai ẩn

	Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng: ax + by < c, ax + by > c, ax + by ≤ c, ax + by ≥ c trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0; x và y là các ẩn số. Mỗi cặp số (x0; y0) sao cho ax0 + by0 < c gọi là một nghiệm của bất phương trình ax + by < c.

Nghiệm của các bất phương trình dạng ax + by > c, ax + by ≤ c, ax + by ≥ c cũng được định nghĩa tương tự.

Ví dụ: Xét bất phương trình x + 2y < 1.

Khi thay x = 0, y = -1 vào vế trái của bất phương trình này thì vế trái có giá trị nhỏ hơn vế phải của nó, vậy bộ hai số (x; y) = (0; -1) là một nghiệm của bất phương trình này.

Dễ thấy rằng, ta có thể tìm được vô số bộ hai số là nghiệm của bất phương trình trên, như vậy bất phương trình trên có vô số nghiệm. Tổng quát hơn, các bất phương trình bậc nhất hai ẩn thường có vô số nghiệm và nếu biểu diễn các nghiệm đó trên mặt phẳng tọa độ thì mỗi nghiệm của bất phương trình bậc nhất hai ẩn là một điểm và tập nghiệm của nó được biểu diễn bởi một tập hợp điểm. Ta gọi tập hợp điểm ấy là miền nghiệm của bất phương trình.

Dưới đây, chúng ta sẽ thấy miền nghiệm của bất phương trình bậc nhất hai ẩn là một nửa mặt phẳng.

Biểu diễn tập nghiệm của bất phương trình bậc nhất hai ẩn

	Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình ax + by < c được gọi là miền nghiệm của bất phương trình đó.

Người ta đã chứng minh được rằng trong mặt phẳng tọa độ Oxy, đường thẳng (d): ax + by = c chia mặt phẳng thành hai nửa mặt phẳng, một trong hai nửa mặt phẳng ấy (không kể bờ (d)) gồm các điểm có tọa độ thỏa mãn bất phương trình ax + by > c, nửa mặt phẳng còn lại (không kể bờ (d)) gồm các điểm có tọa độ thỏa mãn bất phương trình ax + by < c.

Từ đó, suy ra:

Nếu (x₀; y₀) là một nghiệm của bất phương trình ax + by > c (hay ax + by < c) thì nửa mặt phẳng (không kể bờ (d)) chứa điểm M(x₀; y₀) chính là miền nghiệm của bất phương trình đó.

Vậy để xác định miền nghiệm của bất phương trình ax + by < c, ta có quy tắc thực hành biểu diễn hình học tập nghiệm (hay biểu diễn miền nghiệm) như sau:

Bước 1. Vẽ đường thẳng (d): ax + by = c.

Bước 2. Xét một điểm M(x₀; y₀) không nằm trên (d).

• Nếu ax₀ + by₀ < c thì nửa mặt phẳng (không kể bờ (d)) chứa điểm M là miền nghiệm của bất phương trình ax + by < c.
• Nếu ax₀ + by₀ > c thì nửa mặt phẳng (không kể bờ (d)) không chứa điểm M là miền nghiệm của bất phương trình ax + by < c.

CHÚ Ý:

Đối với các bất phương trình dạng ax + by ≤ c hoặc ax + by ≥ c thì miền nghiệm là nửa mặt phẳng kể cả bờ.

VÍ DỤ 1	Xác định miền nghiệm của bất phương trình 3x + y ≤ 0.

Lời giải

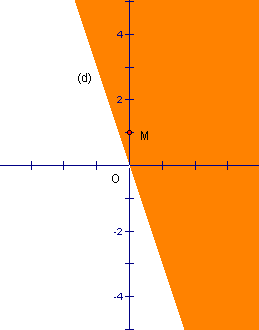
Miền nghiệm của bất phương trình 3x + y ≤ 0 là miền không được tô màu. Trên mặt phẳng tọa độ, đường thẳng (d): 3x + y = 0 chia mặt phẳng thành hai nửa mặt phẳng. Chọn một điểm bất kì không thuộc đường thẳng đó, chẳng hạn điểm M(0;1). Ta thấy (0; 1) không phải là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng chứa bờ (d) và không chứa điểm M(0;1) (Miền không được tô màu trên hình vẽ).

Hoạt động 1	Biểu diễn hình học tập nghiệm của bất phương trình bậc nhất hai ẩn -3x + 2y > 0.

Hệ bất phương trình bậc nhất hai ẩn

Tương tự hệ bất phương trình một ẩn, ta có hệ bất phương trình bậc nhất hai ẩn. Ví dụ:

$(I)\ \ {\begin{cases}3x-y+3>0\\-2x+3y-6<0\\2x+y+4>0.\end{cases}}$

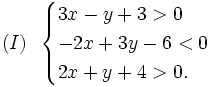
Trong mặt phẳng tọa độ, ta gọi tập hợp các điểm có tọa độ thỏa mãn mọi bất phương trình trong hệ là miền nghiệm của hệ. Vậy miền nghiệm của hệ là giao các miền nghiệm của các bất phương trình trong hệ.

Để xác định miền nghiệm của hệ, ta dùng phương pháp biểu diễn hình học như sau:

• Với mỗi bất phương trình trong hệ, ta xác định miền nghiệm của nó và gạch bỏ (tô màu) miền còn lại.
• Sau khi làm như trên lần lượt đối với tất cả các bất phương trình trong hệ trên cùng một mặt phẳng tọa độ, miền còn lại không bị gạch (tô màu) chính là miền nghiệm của hệ bất phương trình đã cho.

VÍ DỤ 2	Xác định miền nghiệm của hệ bất phương trình (I).

Lời giải	Miền nghiệm của hệ (I) là miền không được tô màu, không kể biên. Trước hết, ta vẽ ba đường thẳng: (d1): 3x - y + 3 = 0; (d2): -2x + 3y - 6 = 0; (d3): 2x + y + 4 = 0. Sau khi tô màu các miền không thích hợp, miền không bị tô màu trên hình vẽ (không kể biên) là miền nghiệm của hệ (I).

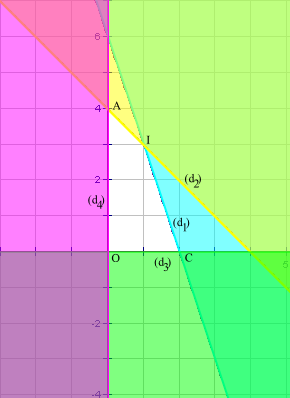
VÍ DỤ 3	Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn: $(II)\ \ {\begin{cases}3x+y\leq 6\\x+y\leq 4\\y\geq 0\\x\geq 0.\end{cases}}$

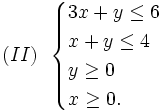Lời giải	Miền nghiệm của hệ (II) là miền tứ giác OAIC, kể cả biên. Vẽ các đường thẳng: (d1): 3x + y = 6; (d2): x + y = 4; (d3): y = 0 (d4): x = 0. Sau khi tô màu các miền không thích hợp, miền tứ giác OAIC, kể cả biên (hình vẽ) là miền nghiệm của hệ (II).

Hoạt động 2	Xác định miền nghiệm của hệ bất phương trình: ${\begin{cases}y-3x>0\\x-2y+5<0\\5x+2y+10>0.\end{cases}}$

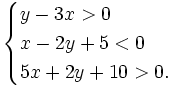Áp dụng vào bài toán kinh tế

Vấn đề tìm miền nghiệm của hệ bất phương trình bậc nhất có liên quan chặt chẽ đến Quy hoạch tuyến tính. Đó là một ngành toán học có nhiều ứng dụng trong đời sống và kinh tế. Sau dây là một số ví dụ đơn giản.

Bài toán 1

Một phân xưởng có hai máy đặc chủng M1, M2 sản xuất hai loại sản phẩm kí hiệu là I và II. Một tấn sản phẩm laọi I lãi 2 triệu đồng, một tấn sản phẩm loại II lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại I phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại II phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ trong một ngày, máy M2 một ngày chỉ làm việc không quá 4 giờ. Hỏi mỗi ngày phải sản xuất bao nhiêu tấn sản phẩm loại I và bao nhiêu tấn sản phẩm loại II để số tiền lãi nhiều nhất.

Phân tích bài toán: Nếu sản xuất x tấn sản phẩm loại I và y tấn sản phẩm loại II trong một ngày (x ≥ 0, y ≥ 0). Như vậy tiền lãi mỗi ngày là L = 2x + 1,6y (triệu đồng) và số giờ làm việc (mỗi ngày) của M1 là 3x + y và máy M2 là x + y.

Vì mỗi ngày M1 chỉ làm việc không quá 6 giờ, máy M2 không quá 4 giờ nên x, y phải thỏa mãn hệ bất phương trình:

$(II)\ \ {\begin{cases}3x+y\leq 6\\x+y\leq 4\\x\geq 0\\y\geq 0.\end{cases}}$

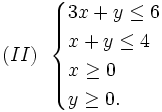
Bài toán trở thành: Tìm các số x và y thỏa mãn hệ bất phương trình (II) sao cho L = 2x + 1,6y lớn nhất.

Bài toán này dẫn đến hai bài toán nhỏ sau:

Bài toán 1. Xác định tập hợp (S) các điểm có tọa độ (x; y) thỏa mãn hệ (II).

Bài toán 2. Trong tất cả các điểm thuộc (S), tìm điểm (x; y) sao cho L = 2x + 1,6y có giá trị lớn nhất.

• Việc giải bài toán 1 chính là việc xác định miền nghiệm của hệ bất phương trình (II) mà ta đã lập và giải ở ví dụ 3.

• Để giải bài toán 2, ta thừa nhận rằng biểu thức L = 2x + 1,6y có giá trị lớn nhất và giá trị ấy đạt được tại một trong các đỉnh của tứ giác OAIC (xem bài đọc thêm). Bằng cách tìm tọa độ các đỉnh O, A, I, C rồi thay vào biểu thức L = 2x + 1,6y ta thấy L lớn nhất khi x = 1, y = 3.

Vậy để có số tiền lãi cao nhất, mỗi ngày cần sản xuất 1 tấn sản phẩm loại I và 3 tấn sản phẩm loại II.

Bài toán 2

Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140kg chất A và 9kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20kg chất A và 0,6kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng, có thể chiết suất được 10kg chất A và 1,5kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II?

Phân tích bài toán. Nếu sử dụng x tấn nguyên liệu loại I và y tấn nguyên liệu loại II thì theo giả thiết, có thể chiết xuất được (20x + 10y) kg chất A và (0,6x + 1,5y) kg chất B. Theo giả thiết, x và y phải thỏa mãn các điều kiện:

• 0 ≤ x ≤ 10 và 0 ≤ y ≤ 9;
• 20x + 10y ≥ 140 hay 2x + y ≥ 14;
• 0,6x + 1,5y hay 2x + 5y ≥ 30.

Tổng số tiền mua nguyên liệu là T = 4x + 3y.

Bài toán trở thành: Tìm các số x và y thỏa mãn hệ bất phương trình:

Miền nghiệm của hệ (III) là miền tứ giác ABCD, kể cả biên.

$(III)\ \ {\begin{cases}0\leq x\leq 10\\0\leq y\leq 9\\2x+y\geq 14\\2x+5y\geq 30.\end{cases}}$

sao cho T = 4x + 3y có giá trị nhỏ nhất.

Bài toán này dẫn đến hai bài toán nhỏ hơn:

Bài toán 1. Xác định tập hợp (S) các điểm có tọa độ (x; y) thỏa mãn hệ (III).

Bài toán 2. Trong tất cả các điểm thuộc (S), tìm điểm (x; y) sao cho T = 4x + 3y có giá trị nhỏ nhất.

• Việc giải bài toán 1 chính là việc xác định miền nghiệm của hệ bất phương trình (III).

• Để giải bài toán 2, ta thừa nhận rằng biểu thức T = 4x + 3y có giá trị nhỏ nhất và giá trị ấy đạt được tại một trong các đỉnh của tứ giác ABCD (xem bài đọc thêm). Bằng cách tìm tọa độ các đỉnh A, B, C, D rồi so sánh các giá trị tương ứng của T, ta được giá trị nhỏ nhất là T = 32 tại điểm A(5; 4).

Vậy để chi phí nguyên liệu ít nhất, cần sử dụng 5 tấn nguyên liệu loại I và 4 tấn nguyên liệu loại II (khi đó, chi phí tổng cộng là 32 triệu đồng).

BÀI TẬP

1) Xác định miền nghiệm của mỗi bất phương trình hai ẩn:

a) x - 2 + 2(y - 1) > 2x + 4;

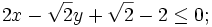
b) $2x-{\sqrt {2}}y+{\sqrt {2}}-2\leq 0;$

2) Xác đình miền nghiệm của các hệ bất phương trình bậc nhất hai ẩn sau:

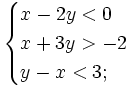
a) ${\begin{cases}x-2y<0\\x+3y>-2\\y-x<3;\end{cases}}$

b) ${\begin{cases}{\cfrac {x}{2}}+{\cfrac {y}{3}}-1>0\\2(x-1)+{\cfrac {y}{2}}<4.\end{cases}}$

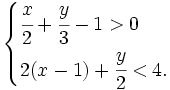
3) Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau:

Nhóm	Số máy trong mỗi nhóm	Số máy trong từng nhóm để sản xuất ra một đơn vị sản phẩm
		Loại I	Loại II
A	10	2	2
B	4	0	2
C	12	2	4

Một đơn vị sản phẩm I lãi 3 nghìn đồng, một đơn vị sản phẩm II lãi 5 nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi cao nhất.

4) Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn (heo) chứa 600 đơn vị potein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất là 1,6kg thịt bò và 1,1kg thịt lợn; giá tiền 1kg thịt bò là 45 nghìn đồng, 1kg thịt lợn là 35 nghìn đồng. Giả sử gia đình đó mua x kilôgam thịt bò và y kilôgam thịt lợn.

a) Viết các bất phương trình biểu thị các điều kiện của bài toán thành một hệ bất phương trình rồi xác định miền nghiệm (S) của hệ đó.

b) Gọi T (nghìn đồng) là số tiền phải trả cho x kilôgam thịt bò và y kilôgam thịt lợn. Hãy biểu diễn T theo x và y.

c) Ở câu a) ta thấy (S) là một đa giác. Biết rằng T có giá trị nhỏ nhất tại (x₀; y₀) với (x₀; y₀) là tọa độ của một trong các đỉnh của (S). Hỏi gia đình đó phải mua bao nhiêu kilôgam thịt mỗi loại để chi phí là ít nhất?

Tài liệu tham khảo

• Sách in:
  • Đại số 10, Nhà xuất bản Giáo dục, 2006, trang 94.
  • Đại số 10 Nâng cao, Nhà xuất bản Giáo dục, 2006, trang 128.
  • Đại số 10, Nhà xuất bản Giáo dục, 2001, trang 89.

Liên kết ngoài

• Bất phương trình - trên Vi.Wikipedia.

---

<<< Đại số 10

Liên kết đến đây

• Đại số 10
• Thành viên:Nguyenthephuc/Note: Đang viết
• Phân phối chương trình môn Toán lớp 10, Trung học phổ thông, Năm học 2006 - 2007