Đại số 8/Chương IV/§5. Phương trình chứa dấu giá trị tuyệt đối
| Đưa về phương trình không chứa dấu giá trị tuyệt đối bằng cách nào? |
Mục lục
Lí thuyết[sửa]
Nhắc lại về giá trị tuyệt đối[sửa]
Giá trị tuyệt đối của số a, kí hiệu là |a|, được định nghĩa như sau:
-
-
- |a| = a khi a ≥ 0;
- |a| = -a khi a < 0.
-
Chẳng hạn: |5| = 5, |0| = 0, |-3,5| = 3,5.
Theo định nghĩa trên, ta có thể bỏ giá trị tuyệt đối tùy theo giá trị của biểu thức ở trong giá trị tuyệt đối là âm hay không âm.
Ví
dụ
1.
Bỏ
dấu
giá
trị
tuyệt
đối
và
rút
gọn
các
biểu
thức
sau:
a) A = |x - 3| + x - 2 khi x ≥ 3;
b) B = 4x + 5 + |-2x| khi x ≥ 0.
Giải:
a)
Khi
x
≥
3,
ta
có
x
-
3
≥
0
nên
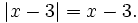 Vậy
A
=
x
-
3
+
x
-
2
=
2x
-
5.
Vậy
A
=
x
-
3
+
x
-
2
=
2x
-
5.
b)
Khi
x
>
0,
ta
có
-2x
<
0
nên
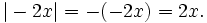 Vậy
B
=
4x
+
5
+
2x
=
6x
+
5.
Vậy
B
=
4x
+
5
+
2x
=
6x
+
5.
Hoạt
động
1.
Rút
gọn
biểu
thức:
a)
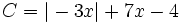 khi
x
≤
0;
khi
x
≤
0;
b)
D
=
5
-
4x
+
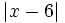 khi
x
<
6.
khi
x
<
6.
Giải một số phương trình chứa dấu giá trị tuyệt đối[sửa]
Ví dụ 2. Giải phương trình |3x| = x + 4.
Giải:
-
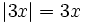 khi
3x
≥
0
hay
x
≥
0;
khi
3x
≥
0
hay
x
≥
0;
-
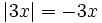 khi
3x
<
0
hay
x
<
0.
khi
3x
<
0
hay
x
<
0.
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
- Phương trình 3x = x + 4 với điều kiện x ≥ 0.
-
Ta
có
3x
=
x
+
4
 2x
=
4
2x
=
4
 x
=
2.
x
=
2.
- Giá trị x = 2 thỏa mãn điều kiện x ≥ 0, nên 2 là nghiệm của phương trình (1).
- Phương trình -3x = x + 4 với điều kiện x < 0.
-
Ta
có
-3x
=
x
+
4
 -4x
=
4
-4x
=
4 x
=
-1.
x
=
-1.
- Giá trị x = -1 thỏa mãn điều kiện x < 0, nên -1 là nghiệm của phương trình (1).
Tổng hợp các kết quả trên, ta có tập nghiệm của phương trình (1) là S = {-1; 2}.
Ví
dụ
3.
Giải
phương
trình
|x
-
3|
=
9
-
2x.
Giải:
- |x - 3| = x - 3 khi x - 3 ≥ 0 hay x ≥ 3;
- |x - 3| = -(x - 3) khi x - 3 < 0 hay x < 3.
Vậy để giải phương trình (2), ta quy về giải hai phương trình sau:
- Phương trình x - 3 = 9 - 2x với điều kiện x ≥ 3.
-
Ta
có
x
-
3
=
9
-
2x
 3x
=
9
+
3
3x
=
9
+
3
 3x
=
12
3x
=
12
 x
=
4.
x
=
4.
- Giá trị x = 4 thỏa mãn điều kiện x ≥ 3, nên 4 là nghiệm của (2).
- Phương trình -(x - 3) = 9 - 2x với điều kiện x < 3.
-
Ta
có
-(x
-
3)
=
9
-
2x
 -x
+
3=
9
-
2x
-x
+
3=
9
-
2x
 x
=
6.
x
=
6.
- Giá trị x = 6 không thỏa mãn điều kiện x < 3, nên 6 không là nghiệm của (2).
Tổng hợp các kết quả trên, ta có tập nghiệm của phương trình (2) là S = {4}.
Hoạt
động
2.
Giải
các
phương
trình
sau:
a) |x + 5| = 3x + 1;
b) |-5x| = 2x + 21.
BÀI TẬP[sửa]
Tài liệu tham khảo[sửa]
- Sách in: Toán 8, tập 2, Nhà xuất bản Giáo dục, 2004, trang 43.

