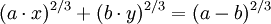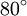Danh mục và lịch sử các đường cong/Phần 2. Từ Co đến Eq (11 – 21)
Mục lục
- 1 11. Conchoid (đường vỏ sò Conchoid)
- 2 12. Conchoid of de Sluze (đường vỏ sò Conchoid Sluze)
- 3 13. Cycloid (đường bánh xe cycloid)
- 4 14. Devil's curve (đường cong quỷ)
- 5 15. Double Folium (đường cong lá đôi)
- 6 16. Durer's shell curve (đường vỏ sò Durer)
- 7 17. Figure Eight Curve (đường cong hình số 8)
- 8 18. Ellipse (đường Ellipse)
- 9 19. Epicycloid (đường Epicycloid)
- 10 20. Epitrochoid (đường Epitrochoid)
- 11 21. Equiangular Spiral (đường xoắn ốc đẳng giác)
- 12 Tham khảo
- 13 Bản quyền
- 14 Mục lục
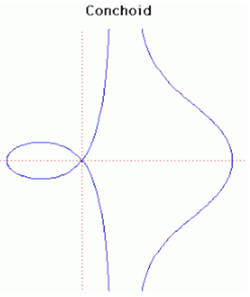
11. Conchoid (đường vỏ sò Conchoid)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
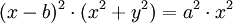
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
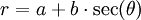
Tên gọi này có nghĩa là dạng vỏ sò do Nicomedes và các nhà toán học Hy Lạp nghiên khoảng 200 trước Công nguyên, liên quan đến bài toán gấp đôi thể tích của khối lập phương. Nicomedes đã xác định được ba dạng khác biệt trong họ đường cong này.
Nicomedes là một nhà hình học trẻ tuổi, khoảng 180 trước Công nguyên. Đường cong vỏ sò do là Pappus đặt tên và xem như là phát minh chính của Nicomedes. Như Nicomedes đã tiên đoán, vào thế kỷ 17 các nhà toán học rất quan tâm đến đường vỏ sò Conchoid và có nhiều ứng dụng vào việc giải quyết các bài toán về nhân đôi khối lập phương và chia một góc làm 3 phần.
Newton đã từng nói rằng nó phải là một đường cong 'chính tắc'. Conchoid có x = b là một tiệm cận đứng và diện tích giới hạn bởi nhánh và tiệm cận là vô hạn. Diện tích của vòng lặp là:
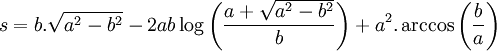
Đường conchoid có nhiều ứng dụng trong việc xây dựng các tòa nhà thời cổ, phần thân của các cột thẳng đứng thường được thực hiện theo hình dạng của các vòng lặp của đường cong này.
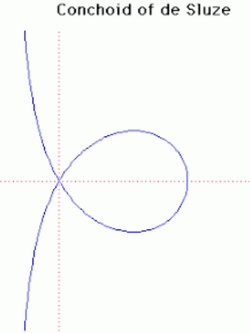
12. Conchoid of de Sluze (đường vỏ sò Conchoid Sluze)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
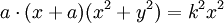
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
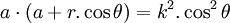
Đường cong này lần đầu tiên được René de Sluze xây dựng vào năm 1662.
René Francois Walter Baron de Sluze vốn là một nhà toán học nhưng có tầm ảnh hưởng rất quan trọng đối với giáo hội. Ông đã góp phần vào việc xác định tính chất hình học của đường xoắn ốc (spiral) và phát minh ra phương pháp chung để xác định điểm uốn của đường cong.
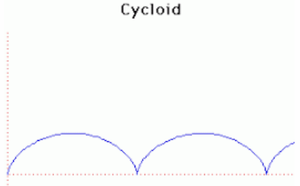
13. Cycloid (đường bánh xe cycloid)[sửa]
Phương
trình
tham
số
trong
hệ
tọa
độ
Descartes:
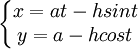
Lấy một đường tròn bán kính = 1, đặt nó lên trục Ox. Lấy một điểm A cố định trên đường tròn đó. Khi đường tròn lăn (không trượt) trên trục Ox, điểm A quay/lăn theo và sẽ vẽ một hình cung, mang tên đường cycloid.
Nếu thay vì lấy một điểm trên đường tròn mà lấy một điểm bên trong đường tròn, sẽ được đường cong gọi tên là curtate cycloid. Năm 1658 Christopher Wren chứng minh rằng nếu đường tròn có chu vi là C thì một chu kỳ đường cycloid có chiều dài 4 C.
Cycloid là quỹ tích của một điểm có khoảng cách h từ tâm của một đường tròn bán kính a có thể lăn không trượt dọc theo một đường thẳng.
- Nếu h < a nó là một cycloid curtate.
- Nếu h > a nó là một cycloid prolate.
- Nếu h = a nó là một cycloid được vẽ ở trên.
Cusa lần đầu tiên nghiên cứu cycloid khi ông đã cố gắng để tìm diện tích của một vòng tròn bằng cách tích phân. Mersenne đã đưa ra định nghĩa thích hợp của cycloid và nêu các tính chất rõ ràng , chẳng hạn như độ dài của các bán kính cơ sở tương đương với chu vi của vòng tròn lăn. Mersenne cũng đã cố gắng để tìm diện tích giới hạn bởi đường cong cycloid nhưng không thành công. Ông đặt ra các câu hỏi để các nhà toán học khác tiếp tục nghiên cứu .
Galileo
đặt
tên
cho
đường
cong
này
vào
năm
1599.
Năm
1639,
ông
đã
viết
cho
Torricelli
về
cycloid,
nói
rằng
ông
đã
nghiên
cứu
các
thuộc
tính
của
nó
trong
suốt
40
năm.
Galileo
đã
cố
gắng
để
tìm
diện
tích
cycloid
bằng
cách
so
sánh
diện
tích
của
vòng
tròn
tạo
ra
nhưng
đã
không
thành
công.
Mersenne
đưa
ra
bài
toán
diện
tích
cycloid
cho
Roberval
năm
1628,
và
mặc
dù
ông
đã
thất
bại
lúc
đầu,
bài
toán
này
đã
được
Roberval
giải
quyết
năm
1634.
Nếu
h
=
a
diện
tích
giới
hạn
bởi
một
cung
cycloid
là
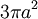 .
Năm
1658
Pascal,
sau
một
thời
kỳ
dành
cho
nghiên
cứu
tôn
giáo,
ông
bắt
đầu
suy
nghĩ
về
các
vấn
đề
trong
lĩnh
vực
toán
học.
Ông
đã
giải
quyết
bài
toán
diện
tích
và
trọng
tâm
của
một
cung
cycloid
bất
kỳ,các
bài
toán
về
diện
tích
và
thể
tích
vật
thể
tròn
xoay
khi
quay
cycloid
quanh
trục
Ox.
.
Năm
1658
Pascal,
sau
một
thời
kỳ
dành
cho
nghiên
cứu
tôn
giáo,
ông
bắt
đầu
suy
nghĩ
về
các
vấn
đề
trong
lĩnh
vực
toán
học.
Ông
đã
giải
quyết
bài
toán
diện
tích
và
trọng
tâm
của
một
cung
cycloid
bất
kỳ,các
bài
toán
về
diện
tích
và
thể
tích
vật
thể
tròn
xoay
khi
quay
cycloid
quanh
trục
Ox.
Năm 1696 Johann Bernoulli, trong Acta eruditorum, đã đưa ra bài toán xét xem những đường cong nào đáp ứng các tính chất brachistochrone. Ông tìm được các tính chất brachistochrone của cycloid và công bố lời giải của mình vào năm 1697. Leibniz, Newton, Bernoulli và de L'Hôpital cũng tập trung nghiên cứu về vấn đề này. Đây là một trong những bài toán biến phân đầu tiên và việc khảo sát này là khởi điểm cho sự phát triển phép tính biến phân (the calculus of variations).Cả hai đường pháp bao ngoài (evolute) và trong (involute) của cycloid đều là một cycloid đồng dạng. Trong thực tế bài toán về đường pháp bao ngoài (evolute) được nghiên cứu bởi Huygens, và cũng từ công trình về cycloid Huygens đã phát triển lý thuyết chung của đường pháp bao ngoài (evolute) của các đường cong.
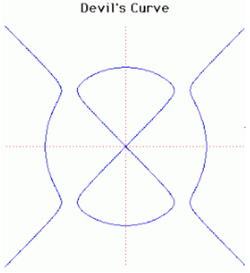
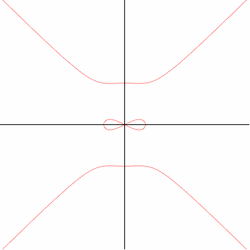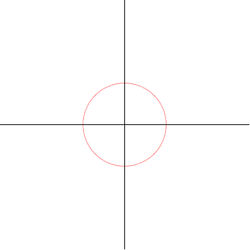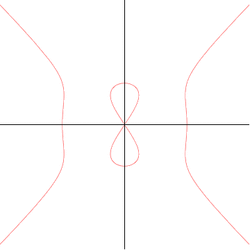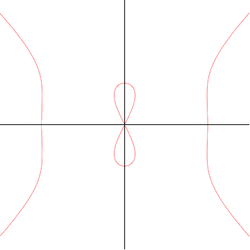
14. Devil's curve (đường cong quỷ)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
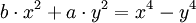
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
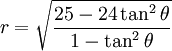
Đường cong quỷ đã được Gabriel Cramer nghiên cứu năm 1750 và Lacroix vào năm 1810. Tên gọi này xuất hiện trong Nouvelles Annalesin năm 1858.
Cramer (1704-1752) là một nhà toán học Thụy Sĩ. Ông trở thành giáo sư toán học tại Giơ-ne-vơ và đã có nhiều công trình liên quan đến vật lý, hình học và lịch sử của toán học. Ông được biết đến với nghiên cứu của mình về định thức (determinants) (1750) nhưng cũng có những đóng góp cho công trình về các đường cong đại số (1750).
15. Double Folium (đường cong lá đôi)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
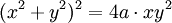
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
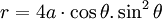
Phương
trình
tổng
quát
đường
hình
lá
được
cho
bởi
công
thức
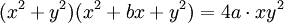
hoặc,
trong
tọa
độ
cực
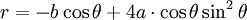
Folium
có
nghĩa
là
hình
lá.
Có
ba
dạng
đặc
biệt
của
hình
lá,
lá
đơn,
lá
đôi
và
lá
ba,
tương
ứng
với
các
trường
hợp:
Nhập
công
thức
toán
vào
đây
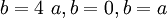 trong
phương
trình
tổng
quát
đường
hình
lá.
trong
phương
trình
tổng
quát
đường
hình
lá.
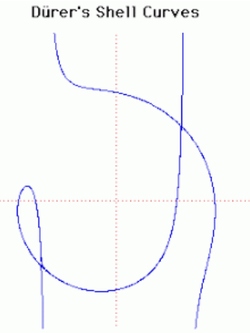
16. Durer's shell curve (đường vỏ sò Durer)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
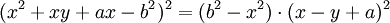
Những đường cong xuất hiện trong công trình của Dürer - Instruction in measurement with compasses and straight edge(1525). (Những kiến thức về đo lường bằng compa và thước kẻ).
Dürer gọi đường cong đó là " ein muschellini "có nghĩa là vỏ sò, nhưng vì nó không giống với đường vỏ sò thực (conchoid) nên ta gọi đó là đường cong vỏ Dürer (muschellini = giống vỏ sò = shell). Có một số trường hợp đặc biệt thú vị: Trong công thức trên, chúng ta có:
b
=
0;
đường
cong
trở
thành
hai
đường
thẳng
trùng
nhau
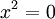
a
=
0;
đường
cong
trở
thành
cặp
đường
thẳng
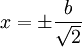 cùng
với
đường
tròn
cùng
với
đường
tròn
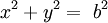
a = b / 2; đường cong có đỉnh tại S(–2a, a).
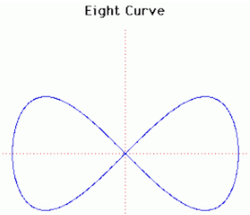
17. Figure Eight Curve (đường cong hình số 8)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
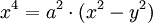
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
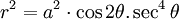
Đường cong này cũng được biết đến như các đường Lemniscate Gerono. Đây là công trình nghiên cứu của Camille-Christophe Gerono (1799 ~ 1891).
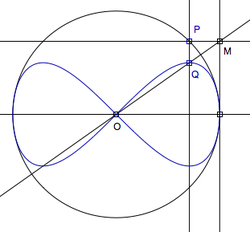
Lemniscate của Gerono còn được gọi là đường cong hình số 8. Nó có thể được xây dựng như sau: cho đường tròn bán kính 1 tâm ở gốc O. P là một điểm trên vòng tròn. M là giao điểm của đường thẳng x = 1 và một đường nằm ngang đi qua P. Gọi Q là giao điểm của OM và đường thẳng đứng qua P. Khi P di chuyển trên đường tròn thì Q vẽ thành đường cong hình số 8.
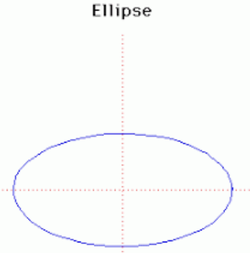
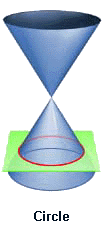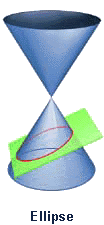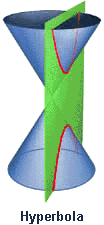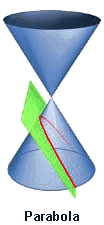
18. Ellipse (đường Ellipse)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
Descartes:
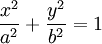
Phương
trình
tham
số
trong
hệ
tọa
độ
Descartes:
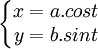
Ellipse lần đầu tiên được nghiên cứu bởi Menaechmus. Euclid cũng đã viết về hình elip và Apollonius đặt tên cho đường cong này như hiện tại.
Pappus
cũng
có
những
đóng
góp
về
tiêu
điểm
và
đường
chuẩn
của
Ellipse.Năm
1602
Kepler
cho
biết
ông
tin
rằng
quỹ
đạo
của
sao
Hỏa
là
hình
bầu
dục,
sau
đó
ông
mới
phát
hiện
ra
rằng
đó
là
một
hình
elip
với
mặt
trời
là
một
trong
những
tiêu
điểm.
Thực
ra,
chính
Kepler
đã
giới
thiệu
từ
"tiêu
điểm"
và
công
bố
phát
hiện
của
ông
vào
năm
1609.
Độ
lệch
tâm
(còn
gọi
là
tâm
sai)
của
quỹ
đạo
hành
tinh
khá
nhỏ
(tức
là
chúng
gần
với
vòng
tròn).
Tâm
sai
của
sao
Hỏa
là
1/11
và
của
Trái
đất
là
1/60.
Năm
1705,
Halley
đã
cho
thấy
rằng
các
sao
chổi,
mà
bây
giờ
được
đặt
tên
của
ông,
di
chuyển
trong
một
quỹ
đạo
hình
elip
mặt
trời.
Tâm
saicủa
sao
chổi
Halley
là
0,9675
do
đó,
nó
gần
giống
một
parabol
(có
tâm
sai
là
1).
Diện
tích
của
hình
elip
là
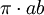 .
Không
có
công
thức
chính
xác
cho
chu
vi
của
một
hình
elip
biểu
diễn
theo
các
hàm
số
sơ
cấp
và
điều
này
đã
dẫn
đến
việc
nghiên
cứu
các
hàm
số
eliptic.
Ramanujan,
trong
năm
1914,
đưa
ra
chu
vi
xấp
xỉ
là
.
Không
có
công
thức
chính
xác
cho
chu
vi
của
một
hình
elip
biểu
diễn
theo
các
hàm
số
sơ
cấp
và
điều
này
đã
dẫn
đến
việc
nghiên
cứu
các
hàm
số
eliptic.
Ramanujan,
trong
năm
1914,
đưa
ra
chu
vi
xấp
xỉ
là
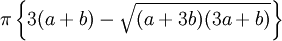
Đường pháp bao ngoài của ellipse với phương trình ở trên là đường cong Lamé.
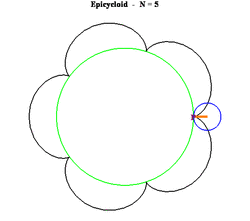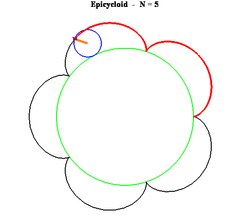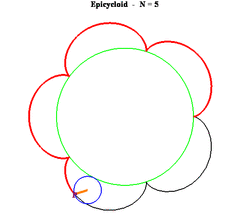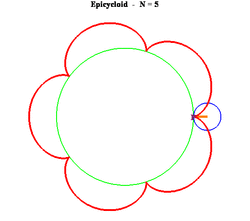
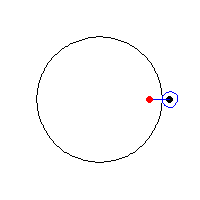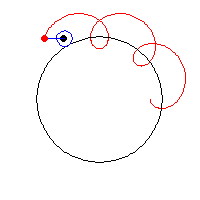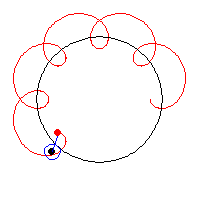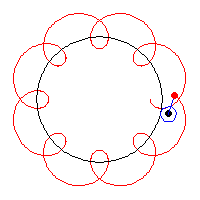
19. Epicycloid (đường Epicycloid)[sửa]
Phương trình tham số trong hệ tọa độ Descartes:
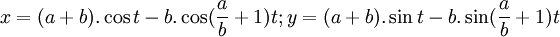
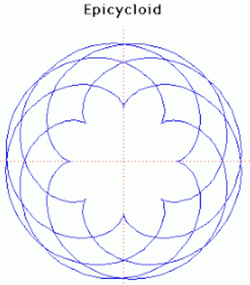
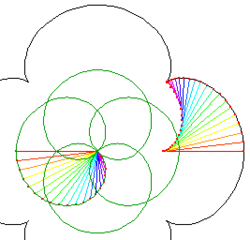
Có bốn đường cong liên quan chặt chẽ đến Epicycloid gồm có Epicycloid, Epitrochoid, Hypocycloid và Hypotrochoid là quỹ tích một điểm P trên đường tròn bán kính b lăn không trượt trên một đường tròn bán kính a cố định. Đối với Epicycloid, một trong số ví dụ được hiển thị ở trên, đường tròn bán kính b lăn bên ngoài của đường tròn bán kính a. P là điểm trên chu vi của đường tròn bán kính b.
Đối với ví dụ ở đây ta có a = 8 và b = 5.
Một số nhà toán học đã quan tâm nghiên cứu đến epicycloid như Dürer (1525), Desargues (1640), Huygens (1679), Leibniz, Newton (1686), de L'Hôpital (năm 1690), Jacob Bernoulli (1690), la Hire (1694), Johann Bernoulli (1695), Daniel Bernoulli (1725), Euler (1745, 1781).
Trường hợp đặc biệt a = b ta có đường cardioid. Nếu a = 2b ta thu được đường cong nephroid.
Nếu
a
=
(m
-
1)
b
với
m
là
một
số
nguyên,
chu
vi
của
epicycloid
là
8bm
và
diện
tích
của
nó
là
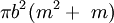
20. Epitrochoid (đường Epitrochoid)[sửa]
Phương trình tham số trong hệ tọa độ Descartes:
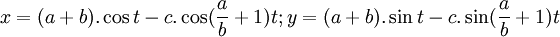
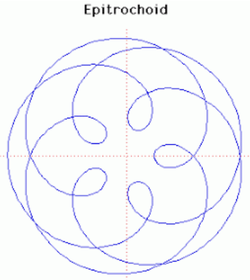
Có bốn đường cong liên quan chặt chẽ với Epitrochoid gồm Epicycloid, Epitrochoid, Hypocycloid và Hypotrochoid. Epitrochoid là quỹ tích điểm P trên một đường tròn bán kính b lăn không trượt trên một đường tròn bán kính a cố định.
Đối với epitrochoid, một trong số ví dụ nêu trên, đường tròn bán kính b lăn không trượt bên ngoài đường tròn bán kính a. P là điểm có khoảng cách là c tính từ tâm của đường tròn bán kính b. Đối với ví dụ này ta có a = 5, b = 3 và c = 5 (P chuyển động bên trong vòng tròn bán kính a).
Một ví dụ về epitrochoid xuất hiện trong công trình của Dürer - Những kiến thức về đo lường bằng compa và thước kẻ (năm 1525). Ông gọi chúng là đường cong nhện. Những đường cong epitrochoid cũng được nghiên cứu bởi la Hire, Desargues, Leibniz, Newton và nhiều người khác.
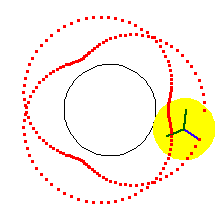
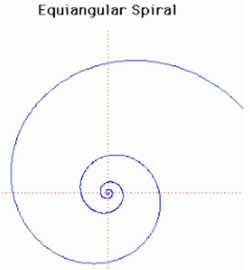
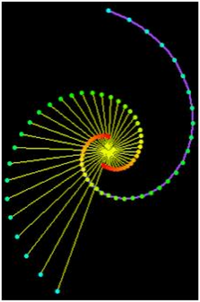
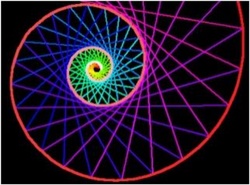
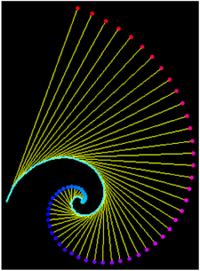
21. Equiangular Spiral (đường xoắn ốc đẳng giác)[sửa]
Phương
trình
đường
cong
trong
hệ
tọa
độ
cực:
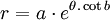
Đường xoắn ốc đẳng giác được phát minh bởi Descartes năm 1638. Trong công trình nghiên cứu độc lập của Torricelli ông cũng đã tìm thấy chiều dài của đường cong này.
|
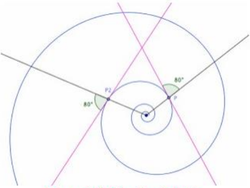
Đường
xoắn
ốc
đẳng
giác
và
cát
tuyến
của
nó
|
|
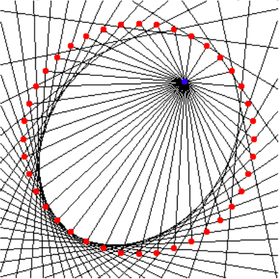
Nếu P là điểm bất kỳ trên đường xoắn ốc thì chiều dài của đường xoắn ốc từ P đến tâm đường cong là hữu hạn, khoảng cách từ P đến cực là d.sec(b) với d là khoảng cách của vector bán kính OP. Jacob Bernoulli vào năm 1692 đã gọi tên đường cong là Spira mirabilis và nó được khắc trên ngôi mộ của ông ở Basel. Hiện tượng tự nhiên này thường xảy ra ở nhiều nơi như vỏ sò, vỏ ốc biển, khi sự phát triển của sinh vật là tỷ lệ thuận với kích thước của sinh vật ấy. Trong cuốn sách " Sự tăng trưởng và hình dạng " của mình, Thompson D'Arcy đã dành cả một chương để đường cong này và mô tả điều xảy ra trong thiên nhiên như là kết quả của cuộn tròn một hình nón trên chính nó, hình ảnh này tương phản với các hình xoắn ốc của Archimedes được hình thành bằng cách cuộn một hình trụ. Đường xoắn ốc tạo ra một góc không đổi b với bất kỳ vector bán kính nào. Trong trường hợp đặc biệt, khi b = π / 2 ta có được một đường tròn. Đối với các đường cong được hiển thị ở trên thì b = 7π/16. Vì vậy chiều dài của đường cong từ một điểm ở khoảng cách d tính từ điểm gốc cùng một vector bán kính là khoảng 5,126 d. Johann Bernoulli cũng đã chứng minh rằng đường pháp bao ngoài (evolute) và trong (involute) của đường xoắn ốc đẳng giác là một đường xoắn ốc đẳng giác đồng dạng.
Tham khảo[sửa]
1. http://www-history.mcs.st-andrews.ac.uk/Curves/Curves.html
2. http://www-history.mcs.st-andrews.ac.uk/
3. Fifty Famous Curves, Lots of Calculus Questions, And a Few Answers. Department of Mathematics, Computer Science, and Statistics,Bloomsburg University Bloomsburg, Pennsylvania 17815.
4. A Handbook on curves and their properties. Robert C. Yates, printed by Edwards Brothers, Inc - Ann Arbor, Michigan U.S.A.
Bản quyền[sửa]
Biên tập và trích dịch.
Ngày 01/04/2012
Mục lục[sửa]
- Giới thiệu
- Phần 1. Từ As đến Co (1 – 10)
- Phần 2. Từ Co đến Eq (11 – 21)
- Phần 3. Từ Fe đến Ka (22 – 32)
- Phần 4. Từ Ka đến Pa (33 – 42)
- Phần 5. Từ Pe đến Rh (43 – 48)
- Phần 6. Từ Ri đến Sp (49 – 53)
- Phần 7. Từ Sp đến Tr (54 – 58)
- Phần 8. Từ Tr đến Wi (59 – 63)
Bài liên quan
Liên kết đến đây
- Danh mục và lịch sử các đường cong
- Bản mẫu:Danh mục và lịch sử các đường cong
- Danh mục và lịch sử các đường cong/Phần 1. Từ As đến Co (1 – 10)
- Danh mục và lịch sử các đường cong/Phần 3. Từ Fe đến Ka (22 – 32)
- Danh mục và lịch sử các đường cong/Phần 4. Từ Ka đến Pa (33 – 42)
- Danh mục và lịch sử các đường cong/Phần 5. Từ Pe đến Rh (43 – 48)
- Danh mục và lịch sử các đường cong/Phần 6. Từ Ri đến Sp (49 – 53)
- Danh mục và lịch sử các đường cong/Phần 7. Từ Sp đến Tr (54 – 58)
- Danh mục và lịch sử các đường cong/Phần 8. Từ Tr đến Wi (59 – 63)