Hình học 10/Chương I/§2. Tổng và hiệu của hai vectơ
Mục lục
Lí thuyết[sửa]
Tổng của hai vectơ[sửa]
|
Cho
hai
vectơ
 và
và
 .
Lấy
một
điểm
O
tùy
ý,
vẽ
.
Lấy
một
điểm
O
tùy
ý,
vẽ
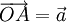 và
và
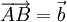 .
Vectơ
.
Vectơ
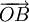 được
gọi
là
tổng
của
hai
vectơ
được
gọi
là
tổng
của
hai
vectơ
 và
và
 .
Ta
kí
hiệu
tổng
của
hai
vectơ
.
Ta
kí
hiệu
tổng
của
hai
vectơ
 và
và
 là
là
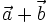 .
Vậy
.
Vậy
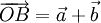 (hình
1-6).
(hình
1-6).Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ. |
|
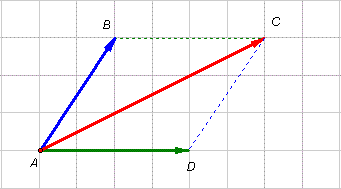
Quy tắc hình bình hành[sửa]
Nếu
ABCD
là
hình
bình
hành
thì
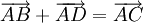 (hình
1-7).
(hình
1-7).
Tính chất của phép cộng các vectơ[sửa]
Với
ba
vectơ
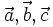 tùy
ý
ta
có:
tùy
ý
ta
có: |
|
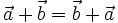 |
(tính chất giao hoán) |
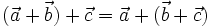 |
(tính chất kết hợp) |
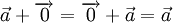 |
(tính chất của vectơ-không). |
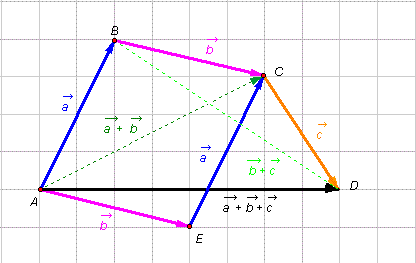
Hình 1-8 dưới đây, minh họa các tính chất trên.
| Hoạt động 1 |
Hãy
kiểm
tra
các
tính
chất
của
phép
cộng
trên
hình
1-8.
|
Hiệu của hai vectơ[sửa]
a) Vectơ đối[sửa]
| Hoạt động 2 |
Vẽ
hình
bình
hành
ABCD.
Hãy
nhận
xét
về
độ
dài
và
hướng
của
hai
vectơ
 và
và
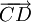
|
Mỗi
vectơ
đều
có
vectơ
đối,
chẳng
hạn
vectơ
đối
của
 là
là
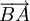 ,
nghĩa
là
,
nghĩa
là
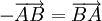 .
.
Đặc
biệt,
vectơ
đối
của
vectơ
 là
vectơ
là
vectơ
 .
.
| VÍ DỤ 1 | |
| Hoạt động 3 |
Cho
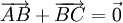 .
Hãy
chứng
tỏ
là
vectơ
.
Hãy
chứng
tỏ
là
vectơ
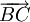 là
vectơ
đối
của
là
vectơ
đối
của
 .
. |
b) Định nghĩa hiệu của hai vectơ[sửa]
| Như vậy: |
|
-
-
- CHÚ Ý
-
-
-
-
- 1) Phép toán tìm hiệu hai vectơ còn được gọi là phép trừ vectơ.
-
2)
Với
ba
điểm
A,
B,
C
tùy
ý
ta
luôn
có:
- Quy tắc trừ hai vectơ cùng điểm đầu (suy ra từ định nghĩa hiệu của hai vectơ)
-
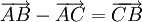 hay
hay
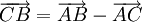
- Quy tắc ba điểm (Quy tắc cộng hai vectơ liên tiếp)
-
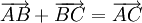 hay
hay
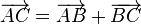
-
-
| VÍ DỤ 2 |
Chứng
minh
rằng:
"Với
bốn
điểm
bất
kì
A,
B,
C,
D
ta
luôn
có:
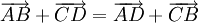 ".
".
Ta có:
Vậy đẳng thức đã cho luôn đúng (đpcm). |
Áp dụng[sửa]
a)
Điểm
I
là
trung
điểm
của
đoạn
thẳng
AB
khi
và
chỉ
khi
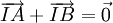 .
.
b)
Điểm
G
là
trọng
tâm
của
tam
giác
ABC
khi
và
chỉ
khi
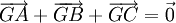 .
.
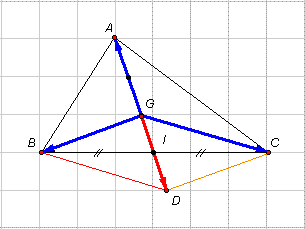
CHỨNG
MINH
b)
- Thuận
- Gọi I là trung điểm của BC.
- Vẽ D là điểm đối xứng với G qua I.
- Từ (1)&(2) suy ra BGCD là hình bình hành.
-
Từ
(3)
suy
ra
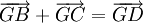
- Từ (2) suy ra G là trung điểm của đoạn thẳng AD.
-
Từ
(5)
suy
ra
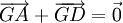 .
. -
Từ
(4)&(6),
ta
có:
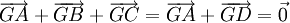 (đpcm).
(đpcm).
- Đảo
Ngược
lại,
giả
sử
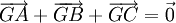 .
Vẽ
hình
bình
hành
BGCD
có
I
là
giao
điểm
của
hai
đường
chéo.
Khi
đó
.
Vẽ
hình
bình
hành
BGCD
có
I
là
giao
điểm
của
hai
đường
chéo.
Khi
đó
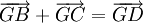 ,
suy
ra
,
suy
ra
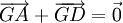 nên
G
là
trung
điểm
của
AD.
Do
đó
ba
điểm
A,
G,
D
thẳng
hàng,
GA
=
2
GI,
điểm
G
nằm
giữa
A
và
I.
Vậy
G
là
trọng
tâm
của
tam
giác
ABC.
nên
G
là
trung
điểm
của
AD.
Do
đó
ba
điểm
A,
G,
D
thẳng
hàng,
GA
=
2
GI,
điểm
G
nằm
giữa
A
và
I.
Vậy
G
là
trọng
tâm
của
tam
giác
ABC.
BÀI TẬP[sửa]
1.
Cho
đoạn
thẳng
AB
và
điểm
M
nằm
giữa
A
và
B
sao
cho
AM
>
MB.
Vẽ
các
vectơ
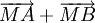 và
và
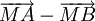 .
.
2.
Cho
hình
bình
hành
ABCD
và
một
điểm
M
tùy
ý.
Chứng
minh
rằng
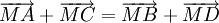 .
.
| 3. Chứng minh rằng đối với tứ giác ABCD bất kì ta luôn có: | |
a)
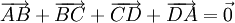
|
b)
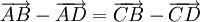 .
. |
4.
Cho
tam
giác
ABC.
Bên
ngoài
của
tam
giác
vẽ
các
hình
bình
hành
ABIJ,
BCPQ,
CARS.
Chứng
minh
rằng
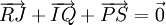 .
.
5.
Cho
tam
giác
đều
ABC
cạnh
bằng
a.
Tính
độ
dài
của
các
vectơ
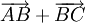 và
và
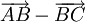 .
.
| 6. Cho hình bình hành ABCD có tâm O. Chứng minh rằng: | |
a)
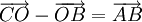
|
b)
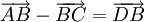
|
c)
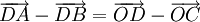
|
d)
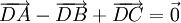
|
7.
Cho
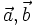 là
hai
vectơ
khác
vectơ
là
hai
vectơ
khác
vectơ
 .
Khi
nào
có
đẳng
thức:
.
Khi
nào
có
đẳng
thức: |
|
a)
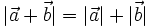
|
b)
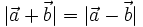
|
8.
Cho
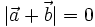 .
So
sánh
độ
dài,
phương
và
hướng
của
hai
vectơ
.
So
sánh
độ
dài,
phương
và
hướng
của
hai
vectơ
 và
và
 .
.
9.
Chứng
minh
rằng
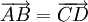 khi
và
chỉ
khi
trung
điểm
của
hai
đoạn
thẳng
AD
và
BC
trùng
nhau.
khi
và
chỉ
khi
trung
điểm
của
hai
đoạn
thẳng
AD
và
BC
trùng
nhau.
10.
Cho
ba
lực
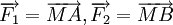 và
và
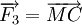 cùng
động
vào
một
vật
tại
điểm
M
và
vật
đứng
yên.
Cho
biết
cường
độ
của
cùng
động
vào
một
vật
tại
điểm
M
và
vật
đứng
yên.
Cho
biết
cường
độ
của
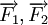 đều
là
100N
và
đều
là
100N
và
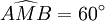 .
Tìm
cường
độ
và
hướng
của
lực
.
Tìm
cường
độ
và
hướng
của
lực
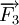 .
.




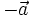 .
.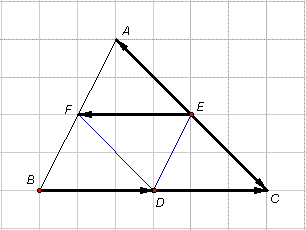
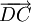 và
và
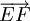 có
cùng
độ
dài
nhưng
ngược
hướng
với
nhau
nên
chúng
là
hai
vectơ
đối
nhau.
Do
đó,
ta
có
thể
viết
có
cùng
độ
dài
nhưng
ngược
hướng
với
nhau
nên
chúng
là
hai
vectơ
đối
nhau.
Do
đó,
ta
có
thể
viết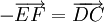 hoặc
hoặc
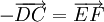
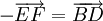 hoặc
hoặc
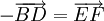
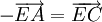 hoặc
hoặc
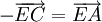
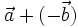 .
Kí
hiệu
.
Kí
hiệu
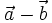 .
.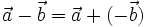

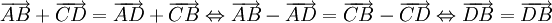 -
luôn
đúng.
-
luôn
đúng.