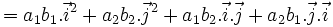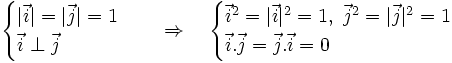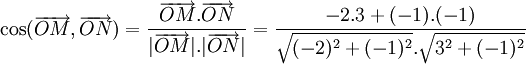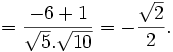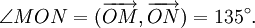Hình học 10/Chương II/§2. Tích vô hướng của hai vectơ
Lí thuyết[sửa]
Góc giữa hai vectơ[sửa]
Cho
hai
vectơ
 và
và
 đều
khác
vectơ
đều
khác
vectơ
 .
.
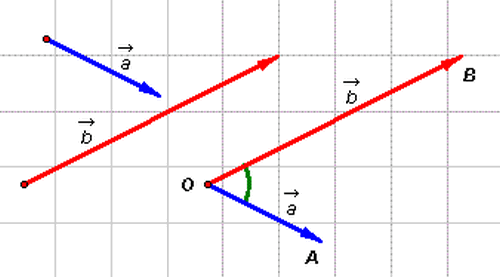
Từ
một
điểm
O
bất
kì,
ta
vẽ
các
vectơ
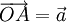 và
và
 (hình
2-6).
Khi
đó:
(hình
2-6).
Khi
đó:
|
Số
đo
của
góc
AOB
được
gọi
là
số
đo
của
góc
giữa
hai
vectơ
 và
và
 ,
hoặc
đơn
giản
là
góc
giữa
hai
vectơ
,
hoặc
đơn
giản
là
góc
giữa
hai
vectơ
 và
và
 .
. |
|
CHÚ
Ý:
-
Góc
giữa
hai
vectơ
 và
và
 được
kí
hiệu
là
được
kí
hiệu
là
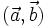 .
. -
Từ
định
nghĩa
ta
có
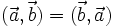
-
Nếu
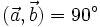 thì
ta
nói
rằng
hai
vectơ
thì
ta
nói
rằng
hai
vectơ
 và
và
 vuông
góc
với
nhau,
kí
hiệu
là
vuông
góc
với
nhau,
kí
hiệu
là
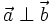 .
. - Trong trường hợp có ít nhất một trong hai vectơ là vectơ-không thì ta xem góc giữa hai vectơ đó là tùy ý (từ 0° đến 180°).
-
Số
đo
của
góc
AOB
là
không
đổi,
dù
ta
có
chọn
điểm
O
ở
các
vị
trí
khác
nhau.
Do
đó,
khi
xác
định
góc
giữa
hai
vectơ
 và
và
 ta
thường
chọn
điểm
O
trùng
với
điểm
gốc
của
vectơ
ta
thường
chọn
điểm
O
trùng
với
điểm
gốc
của
vectơ
 hoặc
vectơ
hoặc
vectơ
 .
Và
theo
định
nghĩa
ta
có:
.
Và
theo
định
nghĩa
ta
có:
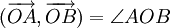 |
| Hoạt động 1 |
Vẽ
và
tính
số
đo
góc
giữa
hai
vectơ
 và
và
 .
Khi:
.
Khi:
a) Hai vectơ đó cùng hướng. b) Hai vectơ đó ngược hướng. |
| VÍ DỤ 1 | |
| Lời giải | |
Tích vô hướng của hai vectơ[sửa]
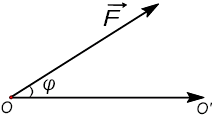
Trong Vật lí, ta có khái niệm "công sinh bởi một lực".
Giả
sử
một
lực
không
đổi
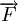 tác
dụng
lên
một
vật
làm
cho
nó
di
chuyển
từ
điểm
O
đến
O'
(hình
vẽ).
tác
dụng
lên
một
vật
làm
cho
nó
di
chuyển
từ
điểm
O
đến
O'
(hình
vẽ).
Khi
đó
lực
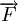 đã
sinh
ra
một
công
A
tính
theo
công
thức:
đã
sinh
ra
một
công
A
tính
theo
công
thức:
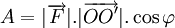
trong đó:
-
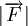 là
cường
độ
của
lực
là
cường
độ
của
lực
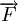 tính
bằng
Niutơn
(kí
hiệu
là
N);
tính
bằng
Niutơn
(kí
hiệu
là
N); -
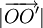 là
độ
dài
vectơ
là
độ
dài
vectơ
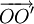 tính
bằng
mét
(kí
hiệu
là
m);
tính
bằng
mét
(kí
hiệu
là
m); -
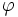 là
góc
giữa
hai
vectơ
là
góc
giữa
hai
vectơ
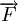 và
và
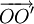 .
. -
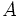 là
công
do
lực
là
công
do
lực
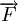 sinh
ra,
được
tính
bằng
Jun
(kí
hiệu
là
J).
sinh
ra,
được
tính
bằng
Jun
(kí
hiệu
là
J).
Trong
Toán
học,
giá
trị
của
biểu
thức
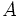 (không
kể
đơn
vị
đo)
được
gọi
là
tích
vô
hướng
của
hai
vectơ
(không
kể
đơn
vị
đo)
được
gọi
là
tích
vô
hướng
của
hai
vectơ
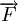 và
và
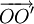 .
Tổng
quát,
ta
có
định
nghĩa
sau
về
tích
vô
hướng
của
hai
vectơ
bất
kì
.
Tổng
quát,
ta
có
định
nghĩa
sau
về
tích
vô
hướng
của
hai
vectơ
bất
kì
 và
và
 .
.
|
Tích
vô
hướng
của
hai
vectơ
 và
và
 là
một
số,
kí
hiệu
là
là
một
số,
kí
hiệu
là
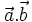 ,
được
xác
định
bởi
công
thức:
,
được
xác
định
bởi
công
thức:
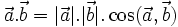 (1)
(1) |
|
| VÍ DỤ 2 |
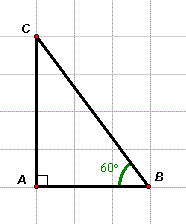
Cho
tam
giác
ABC
vuông
tại
A,
có
BC
=
a
và
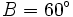 (hình
2-7).
Tính
các
tích
vô
hướng
sau
đây:
(hình
2-7).
Tính
các
tích
vô
hướng
sau
đây:
|
| Lời giải | |
| Hoạt động 2 |
Cho
hai
vectơ
 và
và
 đều
khác
vectơ
đều
khác
vectơ
 .
Khi
nào
thì
tích
vô
hướng
của
hai
vectơ:
.
Khi
nào
thì
tích
vô
hướng
của
hai
vectơ:
a) Bằng 0? b) Có giá trị dương? c) Có giá trị âm? |
-
-
-
- CHÚ Ý
-
Với
 và
và
 khác
vectơ
khác
vectơ
 ,
ta
có:
,
ta
có:
-
-
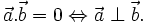 |
| Hai vectơ (khác vectơ không) vuông góc với nhau khi và chỉ khi tích vô hướng của chúng bằng 0. |
Bình phương vô hướng[sửa]
Khi
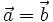 thì
công
thức
(1)
trở
thành:
thì
công
thức
(1)
trở
thành:
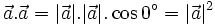
Người
ta
kí
hiệu
tích
vô
hướng
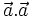 là
là
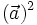 hay
đơn
giản
hơn
là
hay
đơn
giản
hơn
là
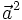 và
gọi
là
bình
phương
vô
hướng
của
vectơ
và
gọi
là
bình
phương
vô
hướng
của
vectơ
 .
.
Như vậy, ta có:
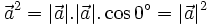
| Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó. |
| Hoạt động 3 |
Đẳng
thức
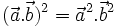 có
đúng
với
mọi
vectơ
có
đúng
với
mọi
vectơ
 và
và
 không?
Trong
trường
hợp
nào
đẳng
thức
đó
đúng?
không?
Trong
trường
hợp
nào
đẳng
thức
đó
đúng? |
Tính chất của tích vô hướng[sửa]
Với
hai
số
thực
a
và
b,
ta
có
ab
=
ba;
a(b
+
c)
=
ab
+
ac.
Vậy
với
hai
vectơ
 và
và
 ,
ta
có
các
tính
chất
tương
tự
hay
không?
,
ta
có
các
tính
chất
tương
tự
hay
không?
|
Với
ba
vectơ
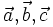 tùy
ý
và
mọi
số
thực
k,
ta
có:
tùy
ý
và
mọi
số
thực
k,
ta
có:
|
|
Ta
dễ
dàng
chứng
minh
được
các
tính
chất
1,
2.
Tính
chất
3
được
thừa
nhận
không
chứng
minh.
Dùng các tính chất của tích vô hướng, ta chứng minh được các hệ thức sau:
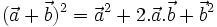 |
(1) |
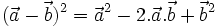 |
(2) |
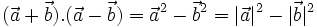 |
(3) |
Chẳng
hạn,
hệ
thức
(3)
được
chứng
minh
như
sau.
Theo
tính
chất
phân
phối,
ta
có:
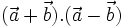 |
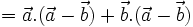 |
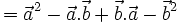 |
|
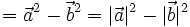 |
| Hoạt động 4 |
Hãy
chứng
minh
các
hệ
thức
(1)
và
(2).
|
Biểu thức tọa độ của tích vô hướng[sửa]
Trên
mặt
phẳng
toạ
độ
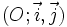 ,
cho
hai
vectơ
,
cho
hai
vectơ
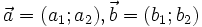 .
.
Khi đó, ta có công thức:
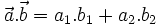 |
Thật
vậy:
NHẬN
XÉT
Hai
vectơ
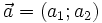 và
và
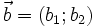 khác
vectơ
khác
vectơ
 vuông
góc
với
nhau
khi
và
chỉ
khi
vuông
góc
với
nhau
khi
và
chỉ
khi
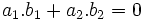
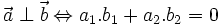 |
| Hoạt động 5 |
Cho
hai
vectơ
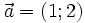 và
và
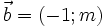 .
Tìm
m
để
hai
đó
vuông
góc
với
nhau?
.
Tìm
m
để
hai
đó
vuông
góc
với
nhau? |
Ứng dụng[sửa]
Từ biểu thức tọa độ của tích vô hướng, ta suy ra một số hệ thức quan trọng sau, cho phép ta tính được: độ dài và góc của hai vectơ khi biết tọa độ của chúng và tính được khoảng cách giữa hai điểm khi biết tọa độ của hai điểm đó.
Độ dài của vectơ[sửa]
Độ
dài
của
vectơ
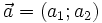 được
tính
theo
công
thức:
được
tính
theo
công
thức:
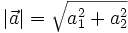 |
Thật
vậy,
ta
có:
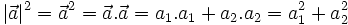
Do
đó
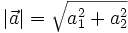 (đpcm).
(đpcm).
Góc giữa hai vectơ[sửa]
Với
hai
vectơ
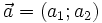 và
và
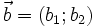 khác
vectơ
khác
vectơ
 ,
từ
định
nghĩa
của
tích
vô
hướng
và
hệ
thức
độ
dài
trên,
ta
suy
ra
góc
giữa
hai
vectơ
được
xác
định
bởi
hệ
thức
sau:
,
từ
định
nghĩa
của
tích
vô
hướng
và
hệ
thức
độ
dài
trên,
ta
suy
ra
góc
giữa
hai
vectơ
được
xác
định
bởi
hệ
thức
sau:
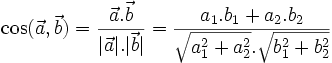 |
| VÍ DỤ 3 |
Cho
hai
vectơ
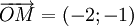 và
và
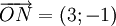 .
Tính
góc
.
Tính
góc
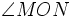 .
. |
| Lời giải | |
Khoảng cách giữa hai điểm[sửa]
Khoảng
cách
giữa
hai
điểm
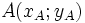 và
và
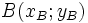 được
tính
theo
công
thức
sau:
được
tính
theo
công
thức
sau:
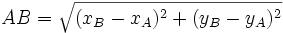 |
Thật
vậy
-
Vì
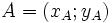 và
và
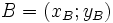 nên
nên
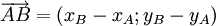
-
Từ
(1)
suy
ra
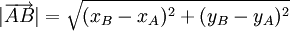
-
Mặt
khác
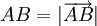 ,
kết
hợp
với
(2)
ta
có
,
kết
hợp
với
(2)
ta
có
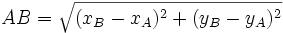 (đpcm)
(đpcm)
| Hoạt động 6 |
Cho
hai
điểm
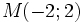 và
và
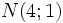 .
.
a) Tính khoảng cách: MO, NO và MN. b) Tìm tọa độ của điểm P nằm trên trục Ox sao cho P cách đều hai điểm M, N. |
BÀI TẬP[sửa]
Góc giữa hai vectơ
1)
Cho
tam
giác
ABC.
Tổng
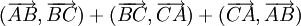 có
thể
nhận
giá
trị
nào
trong
các
giá
trị
sau:
90°;
180°;
270°
và
360°?
có
thể
nhận
giá
trị
nào
trong
các
giá
trị
sau:
90°;
180°;
270°
và
360°?
2)
Cho
hình
vuông
ABCD.
Tính:

3)
Cho
tam
giác
ABC
vuông
ở
A
và
B
=
30°.
Tính
giá
trị
của
biểu
thức
sau:
a)
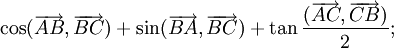
b)
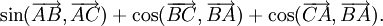
Tích
vô
hướng
của
hai
vectơ
4)
Cho
ba
điểm
phân
biệt
O,
A,
B
thẳng
hàng
và
biết
OA
=
a,
OB
=
b.
Tính
tích
vô
hướng
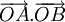 trong
hai
trường
hợp:
trong
hai
trường
hợp:
a) Điểm O nằm ngoài đoạn AB.
b) Điểm O nằm trong đoạn AB.
5)
Cho
tam
giác
vuông
cân
ABC
có
AB
=
AC
=
a.
Tính
các
tích
vô
hướng
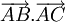 và
và
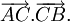
Biểu
thức
tọa
độ
của
tích
vô
hướng
6)
Trong
mặt
phẳng
tọa
độ,
cho
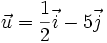 và
và
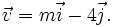
a)
Tìm
các
giá
trị
của
m
để
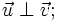
b)
Tìm
các
giá
trị
của
m
để
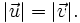
7)
Trên
mặt
phẳng
tọa
độ
Oxy
cho
điểm
A(-2;1).
Gọi
B
là
điểm
đối
xứng
với
điểm
A
qua
gốc
tọa
độ
O.
Tìm
tọa
độ
của
điểm
C
có
tung
độ
bằng
2
sao
cho
tam
giác
ABC
vuông
ở
C.
8)
Trên
mặt
phẳng
Oxy,
hãy
tính
góc
giữa
hai
vectơ
 và
và
 trong
các
trường
hợp
sau:
trong
các
trường
hợp
sau:
a)
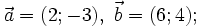
b)
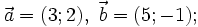
c)
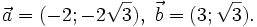
Vận
dụng
tổng
hợp
9) Trên mặt phẳng Oxy, cho hai điểm A(1;3), B(4;2).
a) Tìm tọa độ điểm D nằm trên trục Ox sao cho DA = DB.
b) Tính chu vi tam giác OAB.
c) Chứng tỏ OA vuông góc với AB và từ đó tính diện tích tam giác OAB.
10)
Trong
mặt
phẳng
tọa
độ,
cho
tam
giác
ABC
có
các
đỉnh
A(-4;1),
B(2;4)
và
C(2;-2).
a) Tính chu vi và diện tích của tam giác đó.
b) Tìm tọa độ của trọng tâm G, trực tâm H và tâm I của đường tròn ngoại tiếp tam giác ABC. Từ đó hãy kiểm tra tính thẳng hàng của ba điểm I, G, H.
11)
Trong
mặt
phẳng
tọa
độ,
cho
các
điểm
A
=
(1;1),
B
=
(2;4)
và
C
=
(10;-2).
a) Chứng minh rằng tam giác ABC vuông tại A.
b)
Tính
tích
vô
hướng
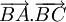
c)
Tính
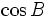 và
và
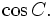
12)
Trên
mặt
phẳng
tọa
độ
Oxy
cho
bốn
điểm
A(7;-3),
B(8;4),
C(1;5)
và
D(0;-2).
Chứng
minh
rằng
tứ
giác
ABCD
là
hình
vuông.
13)
Cho
bốn
điểm
bất
kì
A,
B,
C,
D.
Chứng
minh
rằng:
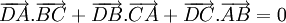
Từ đó suy ra một cách chứng minh định lí: "Ba đường cao của một tam giác đồng quy".
14)
Cho
tam
giác
ABC
với
ba
trung
tuyến
AD,
BE,
CF.
Chứng
minh
rằng:
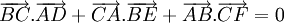
15)
Chứng
minh
rằng
điều
kiện
cần
và
đủ
để
tam
giác
ABC
vuông
tại
A
là:
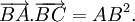
16)
Cho
nửa
đường
tròn
tâm
O
có
đường
kính
AB
=
2R.
Gọi
M
và
N
là
hai
điểm
thuộc
nửa
đường
tròn
sao
cho
hai
dây
cung
AM
và
BN
cắt
nhau
tại
I.
a)
Chứng
minh
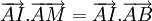 và
và
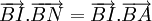
b)
Hãy
dùng
kết
quả
câu
a)
để
tính
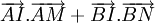 theo
R.
theo
R.
Xem thêm[sửa]
Tài liệu tham khảo[sửa]
-
Sách
in:
- Hình học 10, Nhà xuất bản Giáo dục, 2006, trang 38 và 41.
- Hình học 10 Nâng cao, Nhà xuất bản Giáo dục, 2006, trang 44.
- Hình học 10, Nhà xuất bản Giáo dục, 2001, trang 38.
- Tài liệu giáo khoa thí điểm, Hình học 10, Nhà xuất bản Giáo dục, 1996, trang 30.



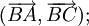
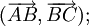
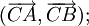
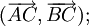
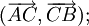
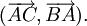
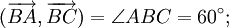
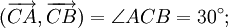
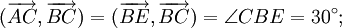
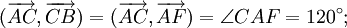
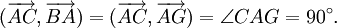
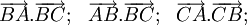
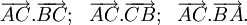
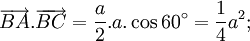
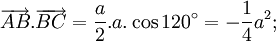

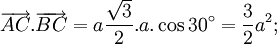
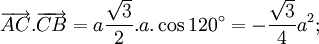
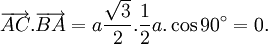
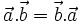 (Tính
chất
giao
hoán)
(Tính
chất
giao
hoán)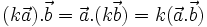
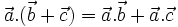 (Tính
chất
phân
phối
đối
với
phép
cộng)
(Tính
chất
phân
phối
đối
với
phép
cộng)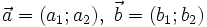
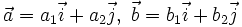 .
.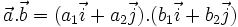 .
.