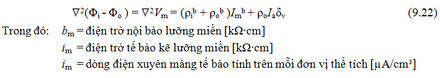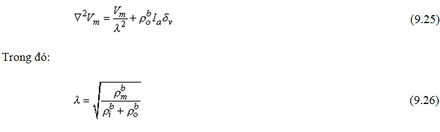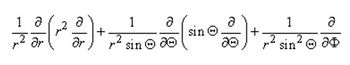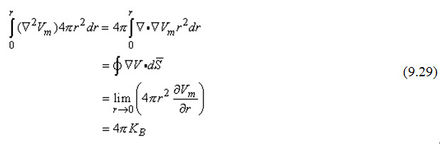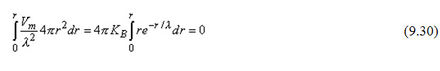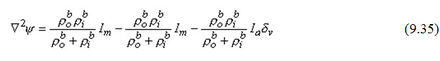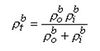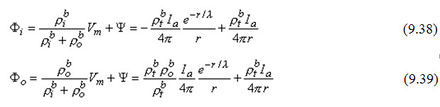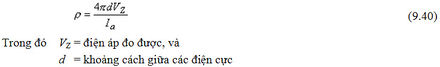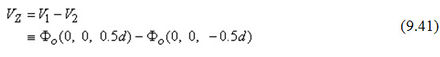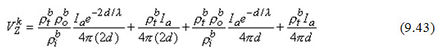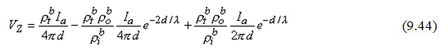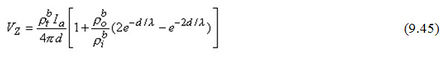Sách:Điện từ sinh học/Mô hình lưỡng miền của các bộ dẫn khối đa tế bào

MÔ HÌNH LƯỠNG MIỀN CỦA CÁC BỘ DẪN KHỐI ĐA BÀO

9.1. Giới thiệu chung

Có nhiều nghiên cứu điện sinh học đề cập tới các mô đa bào. Ví dụ như bó dây thần kinh bao gồm vài nghìn sợi thần kinh; cơ vân cấu thành từ vài nghìn sợi tơ cơ riêng rẽ; tim người có khoảng 10¹⁰ tế bào; não người cũng bao gồm khoảng 10¹⁰ tế bào. Để mô hình hóa cách thức truyền điện của các vùng mô đó, thì điều quan trọng có thể là mô phỏng cấu trúc tế bào riêng rẽ (Spach, 1983). Ngoài ra, xét trong môi trường vĩ mô (lấy trung bình), ta có thể mô phỏng hợp lý các hiện tượng tronh trạng thái hoạt động. Ở trường hợp sau, ta có thể thay thế cấu trúc đa riêng rẽ bằng một thể liên tục trung bình đơn giản hơn rất nhiều. Mục tiêu của chương này là xác định công thức biểu hiện thể liên tục của các hệ thống đa bào và sau đó khai thác các thuộc tính điện trường của nó.

9.2. Cơ tim được coi là một thể liên tục

Các tế bào riêng rẽ của cơ tim là các ống trụ gần tròn có đường kính vào khoảng 10µm và dài khoảng 100 µm. Các tế bào này được xếp lại với nhau như các chồng gạch và được liên kết với nhau thông qua các khớp nối chặt chẽ (giống như “các mối gắn kết chặt chẽ” trong tiếp giáp của các màng tế bào). Ngoài ra còn có các liên kết kẽ tế bào cho phép giao tiếp nội bào. Các liên kết kẽ tế bào đưa ra một liên kết nội bào trực tiếp cho phép các phân tử nhỏ và các ion di chuyển từ không gian nội bào của một tế bào sang nội bào của các tế bào lân cận nó.

Liên kết kẽ tế bào chứa các mạng protein sáu cạnh được gọi là các phần tử kết nối, các phần tử kết nối này ăn sâu vào hai màng tế bào tiếp giáp trước và sau mối nối. Hình thành một rãnh trung tâm tạo ra một đường điện trở cho phép các ion di chuyển giữa các tế bào. Vì số lượng các đường này bị giới hạn và có tiếp diện rất nhỏ nên điện trở của các mối nối đang tồn tại là đáng kể. Trên thực tế, người ta cho rằng điện trở của các mối nối giữa hai tế bào tiếp giáp nhau có cùng giá trị với điện trở tiếp giáp của cơ trương của một trong hai tế bào. Mặt khác, điện trở này có thể giảm xuống dưới 3 lần so với trường hợp dòng điện phải đi qua hai màng tế bào tiếp giáp. Qua đó cho thấy tầm quan trọng trong việc nghiên cứu xâu về liên kết kênh tế bào.

Liên kết kẽ này có độ dài gần bằng độ dài của hai màng plasma mà đường liên kết này đi qua (2x8.5 nm) cộng với khoảng trống giữa các màng tế bào (3 nm) – hay bằng khoảng 20 nm. Độ dài này rất ngắn so với độ dài của bản thân tế bào đó, tỉ lệ bằng khoảng 20x10^-9/100x10^-6 = 2x10^-4. Do tổng các điện trở của mối nối và cơ trương là xấp xỉ bằng nhau nhưng được phân phối trên các độ dài khác nhau theo tỉ lệ 2x10^-4 nên người ta có thể coi rằng điện trở mối nối được tập trung vào một điểm (điện trở riêng phần); trong khi đó, điện trở cơ trương trải ra (phân phối) theo đặc tính của tế bào. Hai dạng cấu trúc điện trở này có tác động khác nhau tới quá trình truyền sóng điện tử; và sẽ được nói đến ở dưới đây.

Một mô phỏng đơn giản về không gian nội bào được thể hiện trong Hình 9.1. Sự phân bổ dòng điện và điện thế trong một tế bào là liên tục. Tuy nhiên, độ dài của liên kết kẽ tương đối ngắn nhưng điện trở của nó lại khá lớn nên liên kết kẽ phải được coi là tương đối riêng biệt và nó khiến điện thế tăng đột ngột, điều này giải thích cho mô hình trong hình 9.1.

Bằng cách giới hạn nghiên cứu vào sự biên thiên dòng điện và điện thế tính trung bình trên đa bào, chúng ta có thể coi vùng nội bào miêu tả trong hình 9.1 gần giống với một bộ dẫn khối liên tục (trung bình) và lấp đầy toàn bộ khoảng không. Điện trở riêng phần và điện trở cơ trương đều được tính đến khi xác định các giá trị trung bình. Kết quả là một môi trường dẫn khối nội bào có tính liên tục.

Hình 9.1. Các tế bào được thể hiện dưới dạng các hình elip giữa chúng có trường điện thế nội bào liên tục. Khoảng không nội bào của các tế bào tiếp giáp nhau được nối liền với nhau bởi các điện trở mối nối (riêng biệt) thể hiện hiệu ứng của các liên kết kẽ tế bào. Trên qui mô một tế bào, điều này tạo ra sự gián đoạn điện thế. Nếu chúng ta giới hạn nghiên cứu vào các biến thiên ở tầm vĩ mô (so với qui mô một tế bào) thì môi trường truyền dẫn có thể được coi là liên tục và lấp đầy mọi khoảng không. Môi trường này được thể hiện qua các thuộc tính trung bình và các điện thế được xác định cũng phải phù hợp với qui mô một tế bào.

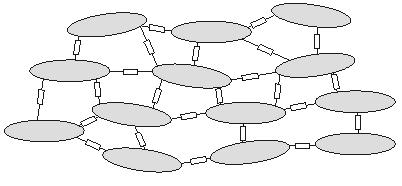
Chúng ta có thể áp dụng những kết quả nghiên cứu này với khoảng kẽ tế bào. Mặc dù trong trường hợp này ta không xét tới sự khác biệt của các khoảng kẽ, tuy nhiên khoảng không đó vẫn bị chia ra bởi sự tồn tại của các tế bào. Các trường liên quan tới thể liên tục này có thể được coi là mức trung bình trên khoảng cách của vài tế bào – giống với khoảng không nội bào.

Tóm lại, ta có thể thay thế mô tim phức tạp bằng các thể liên tục trong nội bào và trong kẽ tế bào, mỗi thể sẽ lấp đầy khoảng không mà mô tim đó chiếm chỗ. Các thông số của thể liên tục bắt nguồn từ mức trung bình phù hợp của cấu trúc thực tế. Cả hai khoảng không được miêu tả bởi hệ thống tọa độ tương đồng. Màng tế bào chia cả hai vùng mô tại mỗi điểm. Mô hình này được miêu tả và được gọi là một mô hình lưỡng miền (Miller and Geselowitz, 1978; Tung, 1978).

Trong một mô hình chính xác hơn, ta có thể đưa ra các biến thiên trường điện và điện thế trên quy mô một tế bào cùng với các biến thiên diễn ra ở những khoảng cách xa hơn. Thông thường, người ta ít quan tâm tới mô hình lưỡng miền khi nghiên cứu phản ứng vĩ mô của mô tế bào và một thể liên tục trung bình liên quan tới các trường trung bình sẽ được chấp nhận và thậm chí còn có thể đơn giản hóa một cách thích hợp.

9.3. Mô tả toán học cho tính không đẳng hướng và lưỡng miền

Mô tả về tính lưỡng miền ở trên dẫn tới các biểu thức toán học đáng tin cậy cho các dòng điện và các điện thế mà trên quan điểm của cấu trúc liên tục là dưới dạng giải tích.

Trước tiên, chúng ta đưa ra khái niệm về độ dẫn điện lưỡng miền (σ^b). Độ dẫn điện nội bào σ_i và ngoại bào σo đã được giới thiệu ở các chương trước là các độ dẫn điện vi mô. Nghĩa là chúng mô tả độ dẫn điện tại một điểm và đối với một môi trường không thuần nhất thì chúng là các hàm của vị trí. (thông thường ta coi σ_o là một hằng số có xu hướng che đậy rằng nó được xác định tại mỗi và mọi điểm). Độ dẫn điện lưỡng miền σ_i^b và σ_o^b là các giá trị trung bình tính trên một số tế bào. Đó là lý do tại sao các độ dẫn điện lưỡng miền phụ thuộc vào cả độ dẫn điện vi mô và hình dạng.

Bây giờ chúng ta khái quát hóa Công thức 7.2 đối với môi trường dẫn điện trung bình không đẳng hướng, theo đó, các vecto mật độ dòng điện theo các hướng x, y và z tỉ lệ với độ biến thiên của hàm điện thế nội bào vô hướng Φ_i theo các hướng tương ứng. Do đó, với miền nội bào, áp dụng định luật Ohm, ta có

Hằng số tỉ lệ (tức là độ dẫn điện lưỡng miền) theo mỗi hướng của trục tọa độ được xem là khác nhau, phản ánh điều kiện chung nhất. Tính không đẳng hướng được thể hiện qua các thông số cấu tạo của mô theo các hướng ưu tiên khác nhau. Trên thực tế, các quan sát thực nghiệm cho thấy các độ dẫn là cao nhất dọc theo các hướng sợi dẫn có liên quan tới hướng mặt cắt sợi cơ.

Tương tự, cũng giả định có tính không đẳng hướng ở đây, ta tính được mật động dòng trong môi trường kẽ tế bào:

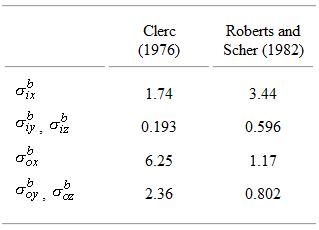
Nhìn chung, các hệ số độ dẫn điện trong nội bào và trong kẽ tế bào là khác nhau; bởi về cơ bản, chúng không có liên quan gì. Các hệ thống đo lường vĩ mô của Clerc (1976) và Roberts và Scher (1982) để xác định các hệ số trong Công thức 9.1 và 9.2 cho cơ tim được cho trong bảng 9.1. Nó thể hiện các phương pháp đo lường hiện có duy nhất để xác định các thông số quan trọng này, tuy nhiên, đáng tiếc là các thông số này lại biến thiên lớn (một phần là do sử dụng các phương pháp khác nhau), do đó, không thể chắc chắn về các giá trị đúng.

Hướng (trục) sợi cơ trong các kết quả này là trục tọa độ x; do sự đồng nhất trong mặt nằm ngang, các suất dẫn theo các hướng y và z là như nhau

Bảng 9.1. Các độ dẫn lưỡng miền của mô tim [mS/cm] được đo bởi Clerc (1976) và Roberts và Scher (1982)

Mật độ dòng nội bào _i (công thức 9.1) và mật độ dòng kẽ tế bào _o (công thức 9.2) kết hợp với nhau do nhu cầu bảo tồn dòng điện. Nghĩa là dòng điện mất đi trong một miền phải được miền kia thu lại. Sự mất (hay thu lại) này được xác định bởi mức độ phân kỳ, do đó,

Tuy nhiên, nhược điểm của mô hình lưỡng miền là tất cả các trường được coi là trung bình về không gian, do đó mất đi sự chuyển hóa. Ngoài ra, phản ứng của tất cả các trường được thể hiện bởi các công thức vi phân 9.1-9.3 cho phép sử dụng các cách tiếp cận toán học hiện có về mặt lý thuyết đối với vật lý toán.

9.4. Cáp một chiều: mô hình lưỡng miền một chiều

Các điều kiện tiên quyết:

Nguồn: Bó các sợi cơ song song, bài toán một chiều

Bộ dẫn: Hữu hạn, không thuần nhất, lưỡng miền không đẳng hướng

Xét một bó lớn gồm các sợi cơ có khía song song nằm trong một môi trường cách ly ví dụ như dầu. Nếu một điện cực bằng kim loại lớn được đặt tại mỗi đầu mút và được cung cấp một dòng điện, đồng thời giả định tất cả các sợi cơ cơ bản có mặt cắt ngang bằng nhau thì phản ứng của mỗi sợi cơ là như nhau. Vì vậy, để nghiên cứu phản ứng của cả bó cơ, ta chỉ cần mô hình hóa bất kì sợi cơ đơn nào rồi thông số hóa cho tất cả các sợi cơ. Một sợi cơ nguyên mẫu như vậy và không gian kẽ tế bào kết hợp với nó được miêu tả trong hình 9.2.

Tiết diện của không gian kẽ tế bào trong hình 9.2 bằng 1/N lần so với tổng tiết diện tế bào kẽ của cả bó sợi cơ, trong đó, N là số lượng các sợi cơ. Thông thường, tiết diện tế bào kẽ nhỏ hơn tiết diện nội bào, do các sợi cơ thường chiếm 70-80% tổng không gian. Do đó, một biểu hiện dòng điện ở thí nghiệm ở hình 9.2 chỉ là mô hình chất truyền dẫn trung tâm tuyến được miêu tả trong hình 3.7 và các công thức 3.41 và 3.42. Trong trường hợp này, là chính xác và phù hợp khi mô hình bao gồm điện trở trục của kẽ tế bào vì dòng điện theo lối này bị cản trở theo hướng trục đó (bởi vì mô hình này dành cho không gian nội bào).

Hình 9.2. Một sợi cơ nguyên mẫu trong một bó cơ nằm trong dầu và phản ứng của nó khi có một dòng diện ổn định. Vì sợi cơ được bịt kín nên dòng điện vào trong không gian nội bào phân bổ dọc theo màng tế bào hình trụ. Tỉ lệ của tế bào kẽ so với tiết diện nội bào của một sợi cơ đơn phản ánh tổng tiết diện của cả bó cơ. Dữ liệu này không thể áp dụng cho chiều dài bởi thông thường tỉ lệ của chiều dài sợi cơ so với đường kính sợi cơ là rất lớn.

Hình 9.3 thể hiện mạch điện mô tả các điều kiện dưới ngưỡng tại trạng thái ổn định. Trong hình này, r_i và r_o tương ứng là các điện trở trục của tế bào và kẽ tế bào trên mỗi đơn vị chiều dài. Với giả định các điều kiện dưới ngưỡng ở trạng thái ổn định, phản ứng của màng tế bào có thể được mô tả bới r_m (Ohm) - một hằng số trở (rò rỉ) nhân với độ dài (nghĩa là: ở trạng thái ổn định, màng tế bào có thành phần điện dung bằng 0, ∂V/∂t = 0, do đó, thành phần điện dung của dòng điện màng tế bào là i_mC = c_m∂V/∂t = 0)

Hình 9.3. Mạch mô hình chất truyền dẫn trung tâm tuyến tương ứng với thí nghiệm trong hình 9.2. Dòng điện ứng dụng ổn định Ia đi vào không gian kẽ tế bào ở bên trái và đi ra ở bên phải (ở các vị trí này I_i = 0). Khi nghiên cứu phản ứng dưới ngưỡng ở trạng thái ổn định, màng tế bào được mô hình hóa như một điện trở. Chỉ rất ít phần tử đầu tiên tại mỗi cực được thể hiện rõ ràng.

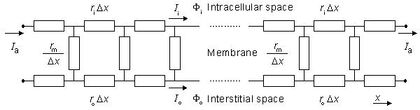
Trên thực tế, hệ thống được mô hình hóa trong hình 9.3 là một thể liên tục. Theo đó, nó có thể được mô tả bởi các công thức vi sai xấp xỉ. Thực chất các công thức này, gọi là các công thức với mô hình cáp, đã được xác định và nhận xét trong chương 3. Cụ thể, ta có:

Trong đó, hằng số không gian, λ, được định nghĩa là:

với đơn vị là cm. Công thức này giống với công thức 3.48.

Trong công thức 9.4 và trong các công thức thuộc chương này dưới đây, V_m là điện thế tương đối của màng tế bào so với điện thể nghỉ. Vì thế, V_m tương đương với V' trong chương 3. Do trong điều kiện nghỉ không có một dòng điện hay một tín hiệu nào (mặc dù vẫn có điện thế xuyên màng tế bào) nên thông thường người ta chỉ quan tâm tới các độ lệch từ điều kiện nghỉ và bỏ qua mọi yếu tố liên quan tới điện thế nghỉ. Lý thuyết này coi điện thế nghỉ bằng 0 mà không cần nêu rõ ràng bởi điều này được thừa nhận rộng rãi. Trong chương nâng cao này, ta thừa nhận thông lệ này và kí hiệu cơ bản V_m

Trong thí nghiệm trong hình 9.2, ta cho rằng dòng điện Ia sẽ vào không gian của kẽ tế bào từ cạnh bên tay trái (x = - l /2), và vì nó đi sang bên phải nên một phần ngang qua màng tế bào để chảy vào không gian nội bào. Quá trình này diễn ra ngược lại trong nửa phải của sợi cơ do sự đối xứng. Điều kiện ràng buộc I_i = 0 tại x = ± l /2 phụ thuộc vào các cực bị bít kín và diện tích màng tế bào tại các cực là phần rất nhỏ so với tổng diện tích. Người ta lập luận rằng, mặc dù dòng điện có thể đi ngang qua các màng tế bào ở cực thì diện tích đó cũng nhỏ tới mức mà dòng điện tương ứng sẽ dường như là rất nhỏ (và có thể bỏ qua); lập luận này lại được minh chứng bởi các nghiên cứu phân tích (Weidmann, 1952). Vì điện thế màng tế bào đơn giản chỉ là dòng điện xuyên màng tế bào tính trên mỗi đơn vị chiều dài nhân với điện trở màng tế bào nhân với độ dài đơn vị (nghĩa là V_m = i_mr_m), nên điều kiện không đối xứng (nghĩa là bằng nhau nhưng trái dấu) của i_m cũng phải thỏa mãn V_m. Do kết quả cho công thức vi phân 9.4 là tổng của các hàm sin và cosin dạng hypecbol và chỉ có dạng hàm sine là đúng nên kết quả cho công thức 9.4 phải là:

Ta đã có các dòng điện trục bên trong và bên ngoài sợi thần kinh trong công thức 3.41 như sau:

Nếu công thức 9.7 được áp dụng cho bất kì cực nào của mạch (x = ± l /2), trong đó, ∂Φi /∂x = 0 và I_o = I_a, ta có

Thay công thức 9.6 vào công thức 9.8, ta được giá trị của K_a là

Từ đó, thay công thức 9.9 vào công thức 9.6, ta được

Ta quan tâm tới kiểm tra phản ứng dòng điện trong tế bào và tế bào kẽ trên độ dài của sợi cơ. Các dòng điện trong tế bào và tế bào kẽ được xác định bằng cách thay công thức 9.10 vào công thức 9.7 a, b, chú ý rằng V_m = Φ_i - Φ_o và rằng các dòng điện trong tế bào và tế bào kẽ bị ràng buộc bởi yêu cầu I_i + Io_{Subscript text} = I_a cho tất cả các x do sự bảo toàn của dòng điện. Kết quả là:

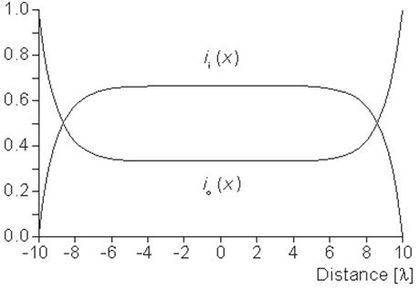
Các dòng điện trong tế bào và tế bào kẽ được miêu tả trong công thức 9.11 và 9.12 biểu thị trong đồ thị 9.4 trong trường hợp l = 20λ và r_i = r_o/2. Một đặc điểm quan trọng là mặc dù toàn bộ dòng điện được ứng dụng trong không gian tế bào kẽ nhưng một phần lại đi ngang qua màng sợi cơ để chảy vào không gian nội bào. (hiện tượng được gọi là tái phân bổ dòng điện). Ta lưu ý rằng việc tái phân bổ dòng điện này từ không gian tế bào kẽ sang không gian tế bào diễn ra trên phạm vi trục của một số lam-đa. Một mặt có thể kết luận rằng nếu độ dài sợi cơ, biểu diễn là các lam-đa, lớn hơn 10, thì trong vùng trung tâm nhất thiêt diễn ra sự tái phân bổ hoàn toàn. Trong vùng này, các mối liên hệ dòng điện-điện thế giống như không có sự hiện hữu của màng tế bào. Thực chất, V_m≈0 và các dòng điện trong tế bào và tế bào kẽ phải cố định và ở quanh trục.

Tổng trở kháng của các điện cực trong sợi cơ có thể được xác định bằng cách chia điện thế ứng dụng V_a[Φ_o(-l /2) - Φ_o(l/2)] cho tổng dòng điện Ia. Giá trị của V_a có thể được tính bằng cách lấy tích phân I_oR_o từ x = -l /2 tới x = l /2 sử dụng công thức 9.12. Kết quả của trở kháng Z này là:

Nếu l>>λ và giả định rằng r_i và r_o có cùng độ lớn, thì số hạng thứ hai trong dấu ngoặc đơn của công thức 9.13 có thể được bỏ qua so với số hạng đầu tiên và kết quả chắc chắn như ước tính nếu không có màng tế bào (một điện trở vùng mô đơn được xác định từ sự đóng góp đồng thời của r_o và r_i). Và nếu l<<λ thì tanh(l/2λ)≈ l/2λ và Z = r_ol, điều này cho thấy không có bất kì sự tái phân bổ dòng điện đáng kể nào; chỉ có không gian tế bào kẽ cung cấp một dòng điện lưu thông. Khi không có bất đẳng thức nào đúng thì Z phản ánh mức độ trung bình của sự tái phân bổ dòng điện.

Ví dụ xem xét ở đây chỉ là một minh họa đơn giản của mô hình lưỡng miền vì hai nguyên nhân. Thứ nhất, nó là bài toán một chiều, do đó đơn giản về mặt toán học. Thứ hai, như ta đã lưu ý, hệ thống được mô hình hóa trên thực tế là một thể liên tục. Do đó, trong khi các mô tim gần giống một thể liên tục và do đó được mô phỏng là một lưỡng miền thì trong trường hợp này, một thể liên tục không chỉ một giả định đơn giản hóa mà trên thực tế còn là một mô phỏng hợp lý của mô tế bào.

Mặc dù ta đã đơn giản hóa hơn nữa các điều kiện dưới ngưỡng và ở trạng thái ổn định, ý tưởng cơ bản về sự tái phân bổ dòng điện giữa không gian trong tế bào và kẽ tế bào kẽ đã sử dụng các điều kiện ít khắt khe hơn. Không cần thiết phải chỉ ra rằng ở bất kì nơi nào nghiên cứu về vùng đa bào thì phản ứng riêng rẽ của tế bào và tế bào kẽ cần phải được xem xét trên quan điểm có sự gián đoạn bắt ngang qua màng tế bào (gọi là V_m). Điều này đúng bất kể trong trường hợp các sợi cơ là riêng rẽ hay liên tục.

Đồ thị 9.4: Sự phân bổ dòng điện quanh trục trong tế bào i_i(x) và trong tế bào kẽ i_o(x) của sợi cơ mô phỏng trong hình 9.2. Tổng độ dài là 20λ và r_i /r_o = ½, Lưu ý rằng các điều kiện trạng thái ổn định áp dụng cho -7λ < x < 7λ, được giả thiết là xấp xỉ bằng 3 λ vì cần có một khu vực cho sự tái phân bổ dòng điện.

9.5. Giải pháp cho nguồn điện trong lưỡng miền đẳng hướng 3 chiều

Các điều kiện tiên quyết:

Nguồn: Khối các sợi cơ, bài toán 3 chiều

Bộ dẫn: Hữu hạn, không thuần nhất, lưỡng miền không đẳng hướng

Để minh họa kĩ hơn mô hình lưỡng miền, ta xét một khối cơ tim và giả định rằng nó có thể được mô hình hóa như một lưỡng miền đồng nhất và đẳng hướng. Do đó, trong công thức 9.1 và 9.2, ta có thể viết:

Ở đây σ_i^b và σ_o^b là giá trị của suất dẫn và ta coi chúng như là các suất dẫn lưỡng miền trong tế bào và kẽ tế bào. Giá trị của chúng có thể được tính như sau. Vì mỗi vùng mô được coi là lấp đầy toàn bộ không gian mô tế vào vốn lớn hơn không gian mà nó thực sự choán chỗ nên σ_i^b và σ_o^b được xác định từ các suất dẫn vi mô σi và σo bằng cách nhân với tỉ lệ của khối lượng thực so với tổng khối lượng. Do đó,

Trong đó: v_c = phần cơ bị các tế bào choán chỗ (= 0.70-0.85).

Trong đó: δ_v là một hàm delta dirac 3 chiều có dạng như sau:

Công thức 9.18 giản lược thành công thức 9.3 nếu I_a = 0.

Thay công thức 9.15 vào công thức 9.18, ta được:

Trong đó: I_m^b = dòng điện xuyên màng tế bào trên mỗi đơn vị thể tích [µA/cm³]. Ta cũng qui định sự bảo toàn của dòng điện (công thức 9.3):

Và thay công thức 9.14 vào công thức 9.20, ta được:

Bây giờ, nhân công thức 9.19 với ρ_o^b (= 1/σ_o^b) và công thức 9.21 với ρ_i^b (= 1/σ_i^b), sau đó cộng hai kết quả lại, ta được:

Với các điều kiện dưới ngưỡng ở trạng thái ổn định, điện dung có thể được bỏ qua, do đó, màng tế bào có tính thuần trở. Nếu tỉ lệ bề mặt so với thể tích của các tế bào là đồng nhất và xác định thì dòng điện xuyên màng tế bào trên mỗi đơn vị thể tích trong trạng thái ổn định (I_m^b) là:

Là điện trở màng tế bào nhân với thể tích [kΩ cm]. (Biến ρ_m^b là độ lớn của suất điện trở vì nó thể hiện sự đóng góp của các màng tề bào vào suất điện trở thoát ra của một vùng bao gồm các không gian trong và ngoài tế bào và các màng tế bào)

Thay công thức 9.23 vào 9.22, ta được công thức vi phân mong muốn cho V_m là:

Hằng số không gian đẳng hướng 3 chiều được xác định theo công thức 9.26 có cùng dạng và cùng độ lớn (cm) như khi ta xác định cho các mô hình một chiều theo công thức 9.5.

Khi xét tới tính cân xứng dạng cầu, V_m (trong công thức 9.25) trong hệ tọa độ cầu có dạng:

Chỉ chứa duy nhất một biến phụ thuộc r, nên chúng ta có:

Kết quả khi r ≠ 0 là

Ta có thể tính tới nguồn hàm delta δ_v bằng cách qui định một điều kiện ràng buộc thích hợp tại gốc. Với quan điểm này, K_B trong công thức 9.28 được chọn để phản ứng của V_m khi r→0 là chính xác. Điều kiện này được đưa ra bằng cách kết hợp mỗi số hạng trong công thức 9.25 qua một khối cầu có bán kính r→0 với tâm là gốc. Tích phân thể tích của số hạng bên tay trái công thức 9.25 được xác định bằng cách chuyển đổi nó sang một tích phân mặt sử dụng định lý phân kỳ của phân tích vecto. Ta có:

(Bước cuối cùng có được bằng cách thay thế công thức 9.28 cho V_m

Thay công thức 9.28 cho V_m trong số hạng thứ hai của công thức 9.25, ta được

Trong khi đó, số hạng thứ 3 là

Công thức 9.31 có được từ định nghĩa hàm delta dirac δ_v có được từ công thức 9.18. Thay các công thức 9.29-9.31 vào 9.25 chứng minh rằng V_m sẽ có phản ứng chính xác trong vùng lân cận r của gốc nếu K_B thỏa mãn:

Thay công thức 9.32 vào 9.28, cuối cùng ta được:

Nếu hàm vô hướng Ψ có dạng

Thì từ công thức 9.19 và 9.21, ta có

Do đó,

Trong đó

và ρ_t^b là tổng trở kháng của mô tế bào trong trường hợp không có màng tế bào (gọi là trở kháng cỡ lớn). Ta lưu ý răng trong công thức 9.36, Ψ thỏa mãn một công thức Poisson (đơn miền). Trên thực tế, Ψ là trường của nguồn điểm tại điểm gốc và bằng:

Vì V_m = Φ_i - Φ_o, ta có thể biểu diễn Φ_i hoặc Φ_o thay cho V_m and Ψ bằng cách sử dụng công thức 9.34. Kết quả là:

Trong đó công thức 9.33 và 9.37 được thay vào công thức 9.38 và 9.39 để có được các biểu thức sau các dấu hiệu ngang bằng thứ hai. Cặp công thức này thể hiện phản ứng của các trường bộ phận. Lưu ý rằng điều kiện ràng buộc ∂Φ_i/∂r = 0 với r→0 đã được thỏa mãn bởi công thức 9.38. Điều kiện này đã được sử dụng khi hình thành công thức 9.19, theo đó, tổng dòng điện nguồn là của tế bào kẽ.

9.6. Phương pháp trở kháng bốn điện cực sử dụng trong lưỡng miền đẳng hướng

Với một mô đẳng hướng đồng nhất, việc xác định điện trở suất của mô đó bằng thực nghiệm thì thường sử dụng phương pháp 4 điện cực (Hình 9.5). Trong phương pháp này, bốn điện cực đặt cách đều nhau được chèn sâu vào mô đó. Chúng ta giả định rằng tổng quy mô của hệ thống điện cực này là nhỏ so với khoảng cách của nó tới một đường biên để bộ dẫn có thể gần như không giới hạn về quy mô (vô hạn). Các điện cực ở phía ngoài mang một dòng điện ứng dụng (ví dụ I_a và –I_a) trong khi đó, các điện cực ở phía trong đo lường điện áp được tạo ra. Điện trở suất p (Heiland, 1940) được tính bởi công thức:

Ưu điểm trong việc sử dụng phương pháp bốn điện cực bắt nguồn từ sự tách bạch giữa chu trình định hướng dòng điện và chu trình đo lường điện thế. Trong quá trình này, ẩn số trở kháng tại bề mặt mô điện cực chỉ quan trọng đối với chu trình đo điện thế, vì nó thêm vào một sai số không đáng kể phụ thuộc vào tỉ lệ của trở kháng điện cực để đưa vào trở kháng của bộ khuếch đại (thông thường lớn hơn gấp nhiều lần).

Với một lưỡng miền đẳng hướng, phương pháp bốn điện cực cũng có thể được dùng để xác định các suất dẫn nội bào bo và suất dẫn khe p_i^b. Trong trường hợp này, tối thiểu hai quan sát độc lập phải được thực hiện vì có hai ẩn số. Nếu chúng ta giả định rằng một dòng điện hiện hành I_a được đặt vào trục z tại một khoảng 3d/2 (ví dụ tại (0,0,1.5d)) và dòng –I_a tại (0,0,1.5d) (như được mô tả trong hình 9.5, theo đó, d là khoảng cách giữa các điện cực liền kề), thì các trường điện khe được tạo ra có thể được tính từ Công thức 9.39 sử dụng sự thay thế. Đặc biệt, chúng ta quan tâm tới điện thể (V_z) được đo bằng các điện cực điện áp, theo đó

Áp dụng công thức 9.39 cho dòng I_a (công thức này giả định nguồn gốc của các tọa độ là tại điểm này) cho thấy nó bổ sung vào V_z một lượng V_z^s được tính như sau:

Hình 9.5: Phương pháp bốn điện cực để xác định trở kháng của mô. Điện cực được gắn vào mô đó. Các nhân tố ở bên ngoài mang dòng điện ứng dụng +-I_a trong khi các nhân tố bên trong đo lường điệp áp được tạo ra (V_Z = V₁ - V₂ ). Các điện cực được đặt cách nhau một khoảng (a) (cách đều nhau). Đối với một domain đơn đẳng hướng đồng nhất, điện trở suất là ρ = 2πdV_Z /I_a.

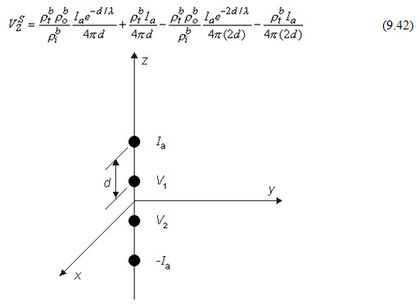
Dĩ nhiên, kết quả là sự độc lập của gốc tọa độ thực sự bởi nó là một thể vật lý đặc biệt. Do đó, điểm chìm (nghĩa là nguồn âm -I_a) góp thêm vào một lượng V_Z^k xác định bởi công thức:

Cộng kết quả của công thức 9.42 và 9.43, điện thế sẽ được đo tại các cực điện thế, gọi là:

Hoặc:

Nếu phép đo V_Z và I_a được thực hiện với d>>λ thì, theo công thức 9.45, điều kiện này sẽ dẫn tới một mối liên hệ

Và có được trở kháng cớ lớn (ρ_t^b = ρ_o^b ρ_i^b /(ρ_o^b + ρ_i^b )). Nếu phép đo thứ hai được thực hiện với d<<λ , thì theo công thức 9.45, ta có:

Và chỉ xác định được trở kháng tế bào kẽ (đúng như dự kiến vì trên một khoảng cách tương đối ngắn, không có dòng điện nào được tái phân bổ sang không gian nội bào, và do đó, chỉ có trở kháng tế bào kẽ tác động tới phản ứng điện thế dòng điện). Hai thí nghiệm này cho phép đưa ra kết luận về cả ρ_o^b và ρ_i^b .

Một kết luận quan trọng rút ra từ chương này được mô tả bởi sự trái ngược của công thức 9.45 và 9.40. Quá trình thực hiện của phương pháp đo bốn cực phụ thuộc vào mô tế bào là đơn miền hay lưỡng miền. Nếu nó là lưỡng miền thì thực hiện theo đơn miền có thể dẫn tới sai lệch đáng kể, đặc biệt nếu d<<λ hay nếu d≈λ. Trường hợp này phải sử dụng công thức 9.45. Nếu mô tế bào là lưỡng miền đẳng hướng thì việc sử dụng mô hình đúng trong phân tích các phép đo 4 cực thậm chí còn quan trọng hơn (nghĩa là công thức 9.45) (Plonsey and Barr, 1986).

REFERENCES

Clerc L (1976): Directional differences of impulse spread in trabecular muscle from mammalian heart. J. Physiol. (Lond.) 225:(2) 335-46. Heiland CA (1940): Geophysical Exploration, 1013 pp. Prentice-Hall, Englewood Cliffs, N.J. Miller WT, Geselowitz DB (1978): Simulation studies of the electrocardiogram, I. The normal heart. Circ. Res. 43:(2) 301-15. Plonsey R, Barr RC (1986): A critique of impedance measurements in cardiac tissue. Ann. Biomed. Eng. 14: 307-22. Roberts DE, Scher AM (1982): Effects of tissue anisotropy on extracellular potential fields in canine myocardium in situ. Circ. Res. 50: 342-51. Spach MS (1983): The discontinuous nature of electrical propagation in cardiac muscle. Ann. Biomed. Eng. 11: 209-61. Tung L (1978): A bidomain model for describing ischemic myocardial D-C potentials. M.I.T. Cambridge, Mass., (Ph.D. thesis) Weidmann S (1952): The electrical constants of Purkinje fibers. J. Physiol. (Lond.) 118: 348-60.

---

Trang trước

Mô hình lưỡng miền của các bộ dẫn khối đa tế bào

Trang tiếp

Liên kết đến đây

• Sách:Điện từ sinh học
• Sách:Điện từ sinh học/Mô hình nơ ron điện tử
• Sách:Điện từ sinh học/Mô hình nguồn trường