The Dirichlet initial-boundary-value problems for sine and sinh-Gordon equations on a half-line

The Dirichlet initial-boundary-value problems for sine and sinh-Gordon equations on a half-line
'
Tạp chí Inverse Problems 2005 August; 21 ():1225-1248
Tác giả	Phạm Lợi Vũ
Nơi thực hiện	Institute of Mechanics, Vietnamese Academy of Science and Technology, 264 Doi Can Street, Hanoi, Vietnam
Từ khóa
DOI   URL  PDF

The paper deals with the problems for the sine-Gordon and sinh-Gordon equations on a half-line:

$v_{{xt}}={\mbox{sin}}\,v,\qquad \ 0\leq x<\infty ,\quad 0\leq t\leq T$

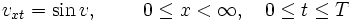(1)

$v_{{xt}}={\mbox{sh}}\,v,\qquad \ \ 0\leq x<\infty ,\quad 0\leq t\leq T$

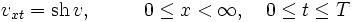(2)

with the given initial and boundary conditions:

$v(x,0)=v(x),\qquad v_{x}(x)\ {\mbox{is a real rapidly decreasing function}}$

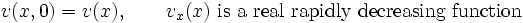(3)

$v(0,t)=h(t),\qquad h(t)\ {\mbox{is a continuous real-valued function}}$

(4)

The Dirichlet initial-boundary-value problem (IBVP) (1), (3), (4) is associated with the scattering problem (SP) for the system

$u_{x}=U_{1}u,\quad U_{1}={{\rm {i}}}\lambda J+{\frac {{\rm {i}}}{2}}{\begin{pmatrix}0&v_{x}\\v_{x}&0\end{pmatrix}},\!\!\qquad 0\leq x<\infty ,\quad 0\leq t\leq T$

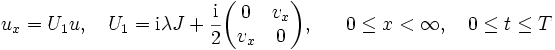(5)

J = diag(1, - 1), u = (u₁, u₂), with the boundary condition:

$u_{1}(0,\lambda )=u_{2}(0,\lambda ).\,$

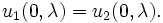(6)

The Dirichlet IBVP (2)–(4) is associated with the SP for the system:

$u_{x}=U_{2}u,\quad U_{2}={{\rm {i}}}\lambda J+{\frac {{\rm {i}}}{2}}{\begin{pmatrix}0&v_{x}\\-v_{x}&0\end{pmatrix}},\qquad 0\leq x<\infty ,\quad 0\leq t\leq T$

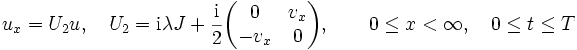(7)

with the boundary condition (6).

We apply a formalism of the direct and inverse SP (5), (6) ((7), (6)) to investigate the considered IBVPs. The difficulty associated with these problems is that the time dependence of the scattering data set s of the SP is determined by unknown boundary values (BVs) at x = 0 of the Jost solutions of (5) ((7)) and more, the evolution equations for BVs contain unknown boundary data (BD). We overcome this difficulty in the following way. We show that the evolution of the BD is described by a linear Volterra integral equation, the solution of which is found in terms of the given (3) and (4). Then the BVs are calculated in terms of (3) and (4). We find the necessary and sufficient conditions on the quantities of the data set s which ensure a unique solution of the inverse problem. Therefore, the antiderivative of the recovered potential is the solution of the considered IBVP.

Bài liên quan

• Ánh sáng là sóng dọc
• Thách thức về khả năng tái lập nghiên cứu
• Nghiên cứu càng rủi ro – thành công càng lớn
• Tỉ lệ logarit
• Vai trò công cụ của logarit qua một số ứng dụng

• « Mới nhất
• ‹ Mới hơn
• Cũ hơn ›

Liên kết đến đây

• Bản mẫu:Lý lịch Khoa học