Thành viên:Nguyenthephuc/Note: Tư duy thuật toán vs Tư duy công thức
Trong Hội thảo các chuyên đề bồi dưỡng HSG giỏi toán duyên hải Trung bộ và Tây nguyên lần thứ tư tại Pleiku hôm 19/4 vừa qua, GS Phạm Huy Điển có nêu một vấn đề hết sức thú vị "Trong giảng dạy toán ở các cấp của ta thường chú ý nhiều đến Tư duy công thức, có một ít dành cho Tư duy logic, nhưng còn hai hình thức tư duy khác thì hầu như bị bỏ trống, đó là Tư duy thống kê và Tư duy thuật toán". Bài viết này được tạo hứng khởi từ bài nói chuyện trên của GS Phạm Huy Điển.
Thực tế thì không hẳn là trong chương trình của ta không đề cập đến tư duy thuật toán. Nhưng quả là càng lên các bậc học cao hơn, tư duy thuật toán càng bị lãng quên, thay vào đó là tư duy công thức máy móc. Ví dụ việc học sinh học các phép toán cộng, trừ, nhân, chia mang tính thuật toán rất rõ. Lợi ích của việc học sinh học cộng, trừ, nhân, chia không chỉ là để chúng biết cộng, trừ, nhân, chia mà quan trọng hơn là để chúng hiểu ý nghĩa của các phép tính đó, cũng như học được tư duy thuật toán trong các phép tính đó. Vì thế, nếu đưa máy tính vào quá sớm sẽ đánh mất của học sinh cơ hội này.
Các bài toán đố kiểu hiệu tỷ, tổng tỷ, tổng hiệu hay những bài toán giải bằng PP giả thiết tạm "Vừa gà vừa chó, bó lại cho tròn, ba mươi sáu con, một trăm chân chẵn" cũng mang tính thuật toán rất cao. Nếu đưa phương trình vào quá sớm sẽ làm cho trẻ không học được những thuật toán thú vị này. Chú rằng Thử và sai là một phương pháp toàn năng hơn lập và giải phương trình nhiều. Nó không chỉ áp dụng được trong Toán học mà còn trong các môn khoa học khác, đặc biệt là trong các tình huống của cuộc sống. (Ví dụ như nấu cơm bỏ bao nhiêu nước thì vừa? Nếu ta mời đám cưới 300 người thì nên đặt bao nhiêu bàn? Để đi học đúng giờ ta phải dậy lúc mấy giờ? ...)
Hay
một
câu
chuyện
khác.
Các
nhà
toán
học
phải
bỏ
ra
khá
nhiều
năm
để
tìm
được
công
thức
giải
phương
trình
bậc
2.
Ngày
trước
việc
giải
phương
trình
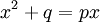 này
được
người
Babylon
mô
tả
như
một
thuật
toán:
này
được
người
Babylon
mô
tả
như
một
thuật
toán:
- Tính một nửa của p.
- Bình phương kết quả.
- Trừ đi q.
- Tính căn bậc hai sử dụng bảng căn bậc hai.
- Cộng kết quả của bước (1) và (4) để có x.
Điều
này
tương
đương
với
công
thức
sau:
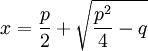 Công
thức
tính
nghiệm
cho
phương
trình
bậc
ba
cũng
được
mô
tả
như
một
thuật
toán
(một
bài
thơ
mà
có
lần
tôi
đã
gửi
lên
FB)
chứ
không
chỉ
là
công
thức
Cardano
khô
khan.
Tóm
tắt
lại
thế
này:
Công
thức
tính
nghiệm
cho
phương
trình
bậc
ba
cũng
được
mô
tả
như
một
thuật
toán
(một
bài
thơ
mà
có
lần
tôi
đã
gửi
lên
FB)
chứ
không
chỉ
là
công
thức
Cardano
khô
khan.
Tóm
tắt
lại
thế
này:
1.
Từ
phương
trình
bậc
3
tổng
quát
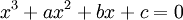 bằng
phép
thế
bằng
phép
thế
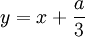 đưa
về
phương
trình
dạng
đưa
về
phương
trình
dạng
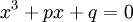
2.
Tìm
u,
v
sao
cho
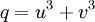 và
và
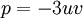 (dùng
định
lý
Viet
đảo
bậc
2).
(dùng
định
lý
Viet
đảo
bậc
2).
3.
Phân
tích
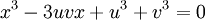 thành
thành
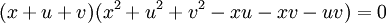 và
giải
tiếp.
và
giải
tiếp.
Tiếp đến người ta cũng tìm ra cách giải cho phương trình bậc 4 (phương pháp Ferrari). Nhưng đến bậc 5 thì mọi cố gắng đi tìm công thức tổng quát đều không đạt được kết quả. Hai nhà toán học Abel và Galois đã góp công trong việc chứng minh không tồn tại công thức tổng quát cho các phương trình đa thức bậc lớn hơn hay bằng 5.
Có
lẽ
chính
từ
đó,
các
nhà
toán
học
đã
rẽ
nhánh
sang
một
hướng
khác,
rõ
ràng
là
thực
dụng
hơn
và
hiệu
quả
hơn.
Thay
vì
tính
chính
xác
thì
tính
gần
đúng.
Tại
sao
ta
cứ
cố
công
đi
tính
chính
xác
khi
thực
tế
cuộc
sống
không
yêu
cầu
ta
phải
làm
điều
đó.
Chẳng
hạn,
bà
bán
vải
ở
chợ
sẽ
nói
gì
với
bạn
nếu
bạn
nói
với
bà
ấy
"Bác
bán
cho
cháu
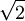 mét
vải"?
mét
vải"?
Thực
tế,
người
ta
có
cách
rất
nhanh
và
hiệu
quả
để
giải
một
phương
trình
đại
số,
chẳng
hạn
phương
trình
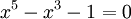 Phương
pháp
đó
gọi
là
chiến
thuật
Chia
để
trị
(Divide
and
Conquer
-
DAC).
Đặt
Phương
pháp
đó
gọi
là
chiến
thuật
Chia
để
trị
(Divide
and
Conquer
-
DAC).
Đặt
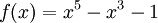 thì
ta
thấy
f(1)
=
-1
<
0,
f(2)
=
23
>
0.
Bây
giờ
ta
sẽ
đi
đến
điểm
giữa
của
đoạn
[1,
2]
là
điểm
3/2
và
tính
f(3/2).
Ta
sẽ
không
tính
cụ
thể
mà
chỉ
nêu
nguyên
tắc:
thì
ta
thấy
f(1)
=
-1
<
0,
f(2)
=
23
>
0.
Bây
giờ
ta
sẽ
đi
đến
điểm
giữa
của
đoạn
[1,
2]
là
điểm
3/2
và
tính
f(3/2).
Ta
sẽ
không
tính
cụ
thể
mà
chỉ
nêu
nguyên
tắc:
1) Nếu f(3/2) = 0 thì 3/2 là nghiệm;
2) Nếu f(3/2) khác 0 thì f(3/2) sẽ trái dấu với một trong hai giá trị f(1) hoặc f(2), ta sẽ thay đoạn [1, 2] bằng đoạn mới có giá trị tại hai đầu mút trái dấu và tiếp tục quá trình cho đến khi:
i) Có 1 a nào đó sao cho f(a) = 0
ii) Số bước đủ lớn (tức là đoạn thẳng đủ nhỏ)
Nếu trường hợp i) xảy ra thì ta có nghiệm (chính xác luôn), còn nếu trường hợp ii) xảy ra thì ta có nghiệm gần đúng với độ chính xác cao tùy ý.
Thuật toán này có thể cài đặt khá dễ dàng bằng các ngôn ngữ lập trình. Thậm chí chỉ cần dùng bảng tính Excel hay máy tính cầm tay Casio cũng có thể cài đặt tốt. Tôi đã từng nhiều lần biểu diễn việc cài đặt này trên các lớp học của tôi và thực tế thì học sinh rất khoái chí.
Tương tự như vậy, việc tính tích phân bằng công thức không phải lúc nào cũng khả thi, nhưng tính bằng các thuật toán số thì luôn thực hiện được với độ chính xác tùy ý.
Như thế, nếu chuyển từ tư duy công thức sang tư duy thuật toán, ta đã mở rộng một cách đáng kể lớp các bài toán mà ta có thể giải được, gia tăng đáng kể tính hiệu quả (thời đại này ai kiểm soát được thời gian là người đó dành chiến thắng).
Bên cạnh đó, ngay cả khi chúng ta dạy các công thức, cũng cần dạy cách đi đến công thức đó, để truyền đạt được tư duy thuật toán, các chuyển bài toán ban đầu về dãy các bài toán con, chứ không chỉ là đưa ra một công thức rồi yêu cầu học sinh áp dụng một cách máy móc. Còn nếu chỉ cần dạy học sinh biết giải pt bậc 2 thì chỉ cần dạy chúng cách nhập số vào máy tính cầm tay (he he, đó cũng là thuật toán :)).
Nguồn: TS Trần Nam Dũng
Liên kết đến đây
Các ghi chú của cùng tác giả
- So sánh điểm kì thi tốt nghiệp trung học của Hà Giang và cả nước
- Học làm cha, làm mẹ
- Đọc sách 2 giờ mỗi ngày (Từ 4-6h sáng)
- Rễ, thân cành, và lá
- Sự trở lại của các thành bang
- Việt Nam học được gì từ bài học Phần Lan trong đổi mới giáo dục
- Đằng sau sự thành công của giáo dục Phần Lan là gì?
- Bí mật trong tuyển chọn và đào tạo giáo viên Phần Lan
- Chiến tranh và khó khăn - lý do khiến giáo dục Việt Nam khó phát triển
- Năng lực và các khái niệm liên quan