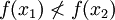Giáo án Giải tích 12/Bài Sự đồng biến, nghịch biến của hàm số

Mọi sự sao chép, trích dẫn toàn văn hay một phần nội dung trang này đều phải ghi rõ nguồn VLOS và tác giả của bài viết này là Nguyễn Thế Phúc.

Nghiêm cấm việc sử dụng lại toàn bộ hay một phần nội dung của trang này với mục đích thương mại.

Mục tiêu[sửa]

Kết thúc bài, học sinh:

Biết hàm số đơn điệu là gì.
Biết mối liên hệ giữa tính đồng biến, nghịch biến của một hàm số và dấu của đạo hàm cấp một của nó.
Biết cách xét tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu đạo hàm cấp một.

Chuẩn bị[sửa]

Giáo viên: Phiếu học tập, bảng phụ

Phiếu học tập

Cho hàm số

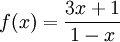f(x)={\frac {3x+1}{1-x}}

và các mệnh đề sau:

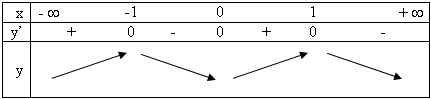
(I): Trên khoảng (2; 3) hàm số f(x) đồng biến.

(II): Trên các khoảng (- ∞; 1) và (1; + ∞) đồ thị của hàm số f(x) đi lên từ trái qua phải.

(III): f(x) > f(2) với mọi x thuộc khoảng (2; + ∞).

Trong các mệnh đề trên có bao nhiêu mệnh đề đúng?

A. 1

B. 3

C. 2

D. 0

Bảng phụ

Tính đạo hàm và xét dấu đạo hàm của hàm số y = x² – 2

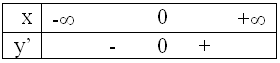
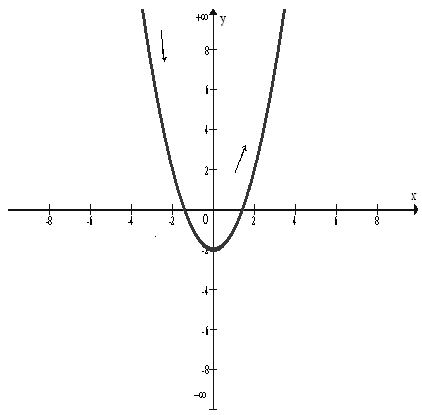
Giải

Ta có y’ = 2x, y’ = 0 ⇔ x = 0

Bảng xét dấu y’

Kết luận:

y’ < 0 trên (-∞; 0)
y’ = 0 tại x = 0
y’ > 0 trên (0; +∞)

Đồ thị của hàm số y = x² – 2

Học sinh: Ôn tập quy tắc xét dấu, SGK, đọc trước bài học

Tiến trình bài dạy tiết 1[sửa]

Ổn định tổ chức:[sửa]

Sĩ số, trang phục, chỗ ngồi, vệ sinh,…

Kiểm tra bài cũ[sửa]

Không

Bài mới[sửa]

*Hoạt động 1 (5 phút): Nhớ lại và mở rộng định nghĩa[sửa]

Nội dung 1
I. Tính đơn điệu của hàm số 1. Mở rộng định nghĩa Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng Hàm số đồng biến: “biến tăng, hàm tăng” Hàm số nghịch biến: “biến tăng, hàm giảm” Hàm số đơn điệu: “hoặc đồng biến hoặc nghịch biến” Đồ thị: Hàm đồng biến, đồ thị đi lên từ trái qua phải Hàm nghịch biến, đồ thị đi xuống từ trái qua phải

Hoạt động của giáo viên	Hoạt động của học sinh
- Đọc mục I.1 SGK và trả lời câu hỏi: + H.số đ.biến trên K là gì? + H.số n.biến trên K là gì? + Mối liên hệ giữa đồ thị và chiều biến thiên của h.số? - Chính xác hóa và ghi bảng Nội dung 1	- Đọc và trả lời: + x₁ < x₂ ⇒ f(x₁) < f(x₂) + x₁ < x₂ ⇒ f(x₁) > f(x₂) + H.số đ.biến ⇒ đ.thị đi lên H.số n.biến ⇒ đ.thị đi xuống - Ghi vở Nội dung 1

*Hoạt động 2 (10 phút): Dạy định lí mối liên hệ giữa “tính đơn điệu và dấu của đạo hàm”[sửa]

Nội dung 2
2. Dấu của đạo hàm và tính đơn điệu Định lí: (SGK) Trên K: f’(x) > 0 ⇒ f(x) đồng biến f’(x) < 0 ⇒ f(x) nghịch biến f’(x) = 0 ⇒ f(x) không đổi Đính lí mở rộng: (SGK) Trên K: f’(x) ≥ 0 và f’(x) = 0 tại một số hữu hạn điểm ⇒ f(x) đồng biến f’(x) ≤ 0 và f’(x) = 0 tại một số hữu hạn điểm ⇒ f(x) nghịch biến

Hoạt động của giáo viên	Hoạt động của học sinh
- Giải ví dụ sau vào vở nháp: Tính đạo hàm và xét dấu đạo hàm của hàm số y = x² – 2 - Treo bảng phụ và nhấn mạnh: Dựa vào dấu y’ và đồ thị, hãy nhận xét mối liên hệ giữa dấu đạo hàm và sự đ.biến, n.biến của h.số? - Thông báo: Kết quả bài toán chính là Nội dung định lí sau ⇒ ghi bảng Nội dung 2	- Giải ví dụ - Trên (0; +∞), y’ >0 thì hàm đ.biến. Trên (-∞; 0), y’<0 thì hàm n.biến. - Ghi vở Nội dung 2

*Hoạt động 3 (15 phút): Dạy quy tắc xét tính đơn điệu[sửa]

Nội dung 3
II. Quy tắc xét tính đơn điệu của hàm số 1. Quy tắc Tìm tập xác định Tính f’(x). Tìm các điểm x_i (i=1,2,…) mà đạo hàm bằng 0 hoặc không xác định. Sắp xếp các điểm x_i theo thứ tự tăng dần và lập bảng biến thiên. Kết luận.

Hoạt động của giáo viên	Hoạt động của học sinh
- Thông báo: Từ hai định lí trên ta có quy tắc xét tính đơn điệu hàm số như sau - Ghi bảng Nội dung 3	- Ghi vở Nội dung 3

Nội dung 4
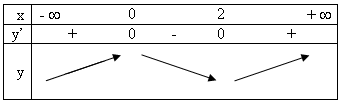
Ví dụ 1: Tìm các khoảng đơn điệu của hàm số y = x³ – 3x² + 2 Lời giải Tập xác định: D = R y’ = 3x(x – 2) y’ = 0 ⇒ x = 0 v x = 2 Bảng biến thiên Hàm số đồng biến trên các khoảng (- ∞; 0) và (2; +∞), nghịch biến trên khoảng (0; 2)

Hoạt động của giáo viên	Hoạt động của học sinh
- Trình bày mẫu ví dụ 1: Nội dung 4 - Nhấn mạnh câu hỏi: “Tại sao ta không được viết là đ.biến trên (- ∞; 0) ∪ (2; +∞)?” - Có thể lấy x₁ < x₂ nhưng $f(x_{1})\not <f(x_{2})$	- Theo dõi, ghi vở Nội dung 4 - Trả lời: vì chỉ có khái niệm hàm số đơn điệu trên K với K là khoảng hoặc đoạn hoặc nửa khoảng, chứ không có K = (a; b) ∪ (c; d),...

*Hoạt động 4 (13 phút): Thực hành quy tắc xét tính đơn điệu[sửa]

Nội dung 5
Ví dụ 2: Tìm các khoảng đơn điệu của hàm số y = -x⁴ + 2x² + 3 Lời giải Tập xác định: D = R y’ = 4x(1 – x)(1 + x) y’ = 0 ⇒ x = 0 v x = -1 v x = 1 Bảng biến thiên Hàm số đồng biến trên các khoảng (- ∞; -1) và (0; 1), nghịch biến trên các khoảng (-1; 0) và (1; +∞)

Hoạt động của giáo viên	Hoạt động của học sinh
- Một em lên bảng, áp dụng quy tắc để giải ví dụ 2. - Quan sát và trợ giúp - Hướng dẫn học sinh cách xét dấu bằng quy tắc “đan dấu”	- Trình bày ví dụ 2 (Nội dung 5) - Tiếp nhận quy tắc đan dấu

*Hoạt động 5 (2 phút): Dặn dò[sửa]

Học:

Định lí và định lí mở rộng
Qui tắc xét tính đơn điệu

Làm bài tập: 1 SGK, tr 9

Tiết trình bài dạy tiết 2[sửa]

đang viết...

Tiết trình bài dạy tiết 3[sửa]

đang viết...

Lưu ý khi sử dụng[sửa]

Sách: Cơ bản
Đối tượng: Trung bình
Phương pháp: Thuyết trình kết hợp vấn đáp gợi mở

Tài liệu tham khảo[sửa]

Giải tích 12, NXB Giáo dục, 2008; tr 4
Tuyển tập các chuyên đề LTĐH môn Toán Hàm số, Trần Phương, 2005; tr 127
Bài giảng “Bài 1. Sự đồng biến, nghịch biến của hàm số”, TS Trần Văn Vuông
Một số tư liệu trên internet không rõ tác giả.

Các bài khác[sửa]

I. PHÂN CHIA THEO HỌC KỲ VÀ TUẦN HỌC[sửa]

Cả năm	78 tiết
Học kỳ I: 19 tuần (72 tiết)	48 tiết 6 tuần đầu x 2 tiết = 12 tiết 10 tuần tiếp x 3 tiết = 30 tiết 3 tuần cuối x 2 tiết = 6 tiết
Học kỳ II: 18 tuần (51 tiết)	30 tiết 6 tuần đầu x 1 tiết = 6 tiết 12 tuần cuối x 2 tiết = 24 tiết

Học kỳ I[sửa]

Chương I – Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số[sửa]

20 tiết

Tiết 1-3	Bài Sự đồng biến, nghịch biến của hàm số
Tiết 4-6	Bài Cực trị của hàm số
Tiết 7-9	Bài Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Tiết 10-11	Bài Đường tiệm cận
Tiết 12-18	Bài Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Tiết 19	Bài Ôn tập chương I
Tiết 20	Bài Kiểm tra chương I

Chương II - Hàm số luỹ thừa, hàm số mũ và hàm số lôgarit[sửa]

17 tiết

Tiết 21-23	Bài Luỹ thừa
Tiết 24-25	Bài Hàm số luỹ thừa
Tiết 26-28	Bài Lôgarit
Tiết 29-31	Bài Hàm số mũ, hàm số lôgarit
Tiết 32-33	Bài Phương trình mũ và phương trình lôgarit
Tiết 34-35	Bài Bất phương trình mũ và lôgarit
Tiết 36	Bài Ôn tập chương II
Tiết 37	Bài Kiểm tra chương II

Chương III - Nguyên hàm, tích phân và ứng dụng[sửa]

16 tiết

Tiết 38-43	Bài Nguyên hàm
Tiết 44-45	Bài Ôn tập học kỳ I
Tiết 46-47	Bài Kiểm cuối học kỳ I
Tiết 48	Trả bài kiểm tra cuối học kỳ I

Học kỳ II[sửa]

Chương III - Nguyên hàm tích phân và ứng dụng (tiếp)[sửa]

Tiết 49-52	Bài Tích phân
Tiết 53-56	Bài Ứng dụng của tích phân
Tiết 57	Bài Ôn tập chương III
Tiết 58	Bài Kiểm tra chương III

Chương IV - Số phức[sửa]

19 tiết

Tiết 59-60	Bài Số phức
Tiết 61-62	Bài Cộng, trừ và nhân số phức
Tiết 63	Bài Phép chia số phức
Tiết 64-65	Bài Phương trình bậc hai với hệ số thực
Tiết 66	Bài Ôn tập chương IV
Tiết 67	Bài Kiểm tra chương IV
Tiết 68	Bài Ôn tập cuối năm
Tiết 69-70	Bài Kiểm tra cuối năm
Tiết 71	Trả bài kiểm tra cuối năm
Tiết 72-78	Tổng ôn tập tốt nghiệp

Xem thêm[sửa]

Thảo luận[sửa]

Liên kết đến đây