Tạo tình huống có vấn đề trong dạy học môn Toán/Tìm sai lầm trong lời giải

Từ VLOS
Bước tới: chuyển hướng, tìm kiếm
Tìm sai lầm trong lời giải và sửa chữa sai lầm đó

Hình thành quy tắc nhân hai vế của một bất đẳng thức với một số âm.‎

Bài toán: Chứng minh rằng: “Bất kì số nào cũng không lớn hơn 0”

Thật vậy, giả sử a là một số thực bất kì:

  • Nếu số a là số âm thì điều đó là hiển nhiên a < 0. ‎
  • Nếu số a là số không thì a = 0.
  • Nếu số a là số dương thì ta có: a – 1 < a khi đó nhân cả hai vế của bất đẳng thức này với –a ta được: -a2 + a < -a2 và thêm a2 vào hai vế của bất đẳng thức ta được: -a2 + a + a2 < -a2 + a2 \Rightarrow a < 0.

Vậy trong mọi trường hợp ta đều có a ≤ 0 (đpcm).

Hình thành khái niệm hàm số hợp và công thức đạo hàm của hàm số hợp

  • Sau khi học sinh biết công thức đạo hàm của một số hàm số thường gặp và các quy tắc tính đạo hàm tương ứng. Giáo viên tổ chức và yêu cầu học sinh tính đạo hàm của các hàm số sau:
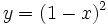
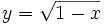
a) y=(1-x)^{2}\, b) y={\sqrt {1-x}}
  • Chia lớp làm 4 nhóm:
    • Nhóm 1: tính đạo hàm câu a bằng định nghĩa.
    • Nhóm 2: tính đạo hàm câu a bằng công thức hàm số thường gặp.
    • Nhóm 3: tính đạo hàm câu b bằng định nghĩa.
    • Nhóm 4: tính đạo hàm câu b bằng công thức hàm số thường gặp.
  • Giáo viên tổ chức cho các nhóm trao đổi, so sánh kết quả và tìm sai lầm trong lời giải.
  • Từ đó đi đến kết luận: “Không áp dụng công thức đạo hàm của các hàm số thường gặp cho các hàm số này được” vì đó không phải là các hàm số thường gặp.
  • Vậy chúng được gọi là các hàm số gì và muốn tính đạo hàm của các hàm số đó ta phải áp dụng công thức nào?

Tìm chỗ sai trong lời giải sau đây và đưa ra lời giải đúng.[1]

Giải phương trình: 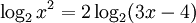\log _{2}x^{2}=2\log _{2}(3x-4) (1)

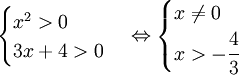
Điều kiện: {\begin{cases}x^{2}>0\\3x+4>0\end{cases}}\Leftrightarrow {\begin{cases}x\neq 0\\x>-{\cfrac 43}\end{cases}}

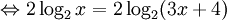
Khi đó: (1) \Leftrightarrow 2\log _{2}x=2\log _{2}(3x+4)

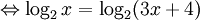
\Leftrightarrow \log _{2}x=\log _{2}(3x+4)

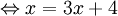
\Leftrightarrow x=3x+4

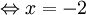
\Leftrightarrow x=-2

Giá trị x = -2 không thỏa mãn điều kiện trên nên phương trình đã cho vô nghiệm.

Khi dạy phần bất phương trình ở lớp 10 có thể cho HS giải bài tập sau:

Khi giải bất phương trình 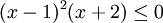(x-1)^{2}(x+2)\leq 0 (1), bạn Hòa đã giải như sau:

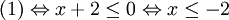(1)\Leftrightarrow x+2\leq 0\Leftrightarrow x\leq -2 (2)

Vậy tập nghiệm của bất phương trình đã cho là \{x|x<-2\}

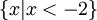
Xét xem lời giải trên đã đúng chưa? Nếu chưa đúng, hãy sửa lại.

Khi giải bài toán này, HS được đặt vào một tình huống gợi vấn đề với nhiệm vụ là phát hiện nguyên nhân và sửa chữa sai lầm. Đó là một tình huống gợi vấn đề vì đối chiếu với ba điểu kiện của tình huống gợi vấn đề, ta thấy:

  1. HS chưa có sẵn câu trả lời và cũng không biết một thuật giải nào để có câu trả lời
  2. HS có nhu cầu giải quyết vấn đề, họ không thể chấp nhận để nguyên nhân sai lầm mà không sửa chữa
  3. Vấn đề này liên quan đến những kiến thức sẵn có của họ, không có gì vượt quá yêu cầu, họ thấy nếu tích cực suy nghĩ vận dụng kiến thức đã học thì có thể tìm ra nguyên nhân sai lầm và sửa chữa sai lầm.

Tài liệu tham khảo[sửa]

  1. ↑ Tài liệu Bồi dưỡng thường xuyên giáo viên Trung học phổ thông chu kì III (2004-2007) Toán học, Bùi Văn Nghị - Vương Dương Minh – Nguyễn Anh Tuấn, NXB Đại học Sư phạm, 2005, trang 134

Xem thêm[sửa]

← Mục lục

  • « Mới nhất
  • ‹ Mới hơn
  • Cũ hơn ›

Liên kết đến đây

Lấy từ “https://tusach.thuvienkhoahoc.com/index.php?title=Tạo_tình_huống_có_vấn_đề_trong_dạy_học_môn_Toán/Tìm_sai_lầm_trong_lời_giải&oldid=101966”