Tạo tình huống có vấn đề trong dạy học môn Toán/Từ cũ đến mới
Chúng ta đã biết điều kiện để một phương trình bậc hai vô nghiệm là biệt thức Delta của nó phải âm. Còn đối với một bất phương trình bậc hai thì sao! Điều kiện gì để một bất phương trình bậc hai vô nghiệm?
Hình thành phương pháp giải toán bằng phương trình
Giải bài tập sau đây bằng phương pháp giả thiết tạm:
-
- “Vừa gà vừa chó
- Bó lại cho tròn
- Ba mươi sáu con
- Một trăm chân chẵn”.
Hỏi có mấy con gà, mấy con chó?
Sau khi học sinh giải xong bằng phương pháp giả thiết tạm đã biết, giáo viên đặt vấn đề “phiên dịch” ngôn ngữ thông thường sang ngôn ngữ Đại số, từ đó dẫn đến kiến thức mới: “Giải bài toán bằng phương trình”.
Hình thành khái niệm phương trình tham số của đường thẳng.
Giải
bài
toán:
“Cho
đường
thẳng
d
đi
qua
điểm
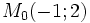 và
có
vectơ
chỉ
phương
và
có
vectơ
chỉ
phương
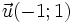 .
Điểm
M(1;2)
có
nằm
trên
đường
thẳng
d
không?”.
.
Điểm
M(1;2)
có
nằm
trên
đường
thẳng
d
không?”.
Dự kiến:
- Nếu học sinh trả lời “Viết phương trình tổng quát của đường thẳng rồi thay tọa độ của M vào phương trình đó” thì giáo viên công nhận là đúng. Liệu có cách nào khác, không cần viết phương trình tổng quát của đường thẳng d.
- Nếu học sinh trả lời “Viết phương trình tham số của đường thẳng d” thì giáo viên có thể hỏi lại “vậy phương trình tham số của đường thẳng là gì... đó chính là nội dung bài học hôm nay”.
-
Sau
đó
phát
biểu
bài
toán
tổng
quát:
“Cho
đường
thẳng
d
đi
qua
điểm
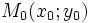 và
có
vectơ
chỉ
phương
và
có
vectơ
chỉ
phương
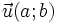 .
Tìm
điều
kiện
để
điểm
M(x;y)
nằm
trên
đường
thẳng
d.
.
Tìm
điều
kiện
để
điểm
M(x;y)
nằm
trên
đường
thẳng
d.
Nhận xét: Cách dạy này có hai chức năng: một là kiểm tra bài cũ tạo tiền đề, hai là tạo ra một vấn đề từ đó đi đến kiến thức mới. Với hai chức năng như thế giúp cho học sinh thấy được mối liên hệ giữa kiến thức cũ và kiến thức mới một cách trực quan. Hiểu được nguồn gốc và bản chất của kiến thức.
Hình thành các quy tắc tính đạo hàm
Sau khi học sinh biết đạo hàm của một số hàm số thường gặp. Giáo viên có thể đặt vấn đề như sau để dẫn đến các quy tắc tính đạo hàm của hàm số:
Ta
đã
biết
đạo
hàm
của:
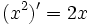 và
và
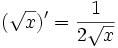 thế
còn:
thế
còn:
|
|
(đạo hàm của một tổng) |
|
|
(đạo hàm của một hiệu) |
|
|
(đạo hàm của một tích) |
|
|
(đạo hàm của một thương) |
Hình thành các phép toán giới hạn của hàm số
Cách đặt vấn đề giống như ví dụ hình thành các quy tắc tính đạo hàm.
Hình thành khái niệm hai phân số bằng nhau (lớp 6)
Đặt vấn đề:
- Ở lớp 5 ta đã biết thế nào là hai phân số bằng nhau với tử số và mẫu số là các số tự nhiên.
-
Thế
còn
đối
với
các
phân
số
mà
tử
số
và
mẫu
số
là
các
số
nguyên
thì
sao,
ví
dụ:
hai
phân
số
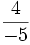 và
và
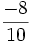 có
bằng
nhau
không
và
làm
thế
nào
để
biết
điều
đó?
có
bằng
nhau
không
và
làm
thế
nào
để
biết
điều
đó? - Đó chính là nội dung của bài học hôm nay!
Hình thành khái niệm phép chia có dư
Sau khi học sinh biết thế nào là phép chia hết, giáo viên tổ chức cho học sinh quan sát: “Hai phép chia sau:
có gì khác nhau?”
Dự kiến:
- Nếu học sinh trả lời “số bị chia khác nhau” thì GV “đúng vậy” và còn gì khác nữa?
- Nếu học sinh trả lời “số dư khác nhau” thì GV “đúng vậy, chính xác hơn là ở phép chia thứ nhất số dư bằng không còn ở phép chia thứ hai số dư khác không”.
- Từ đó giới thiệu phép chia hết, phép chia có dư.
Nhận xét: GV nên cho học sinh quan sát không chỉ với hai phép chia mà càng nhiều càng tốt trong đó chia ra làm hai loại. Loại có dư và loại không có dư. Biện pháp tổ chức tối ưu là cho làm việc nhóm trong đó mỗi thành viên của nhóm tự cho một phép chia.
Hình thành khái niệm phép trừ
Tình huống:
Xét xem có số tự nhiên x nào mà
-
-
- a) 2 + x = 5 hay không?
- b) 6 + x = 5 hay không?
-
Học sinh tìm giá trị của x:
- Ở câu a, tìm được x = 3
- Ở câu b, không tìm được giá trị của x.
Nhận xét: ở câu a ta có phép trừ: 5 – 2 = 3
Khái quát và ghi bảng:
-
- Cho hai số tự nhiên a và b, nếu có số tự nhiên x sao cho b + x = a thì có phép trừ a – b = x.
Hình thành khái niệm phép chia hết (dạy tương tự khái niệm phép trừ)
Tình huống:
Xét xem có số tự nhiên x nào mà
-
-
- a) 3.x = 12 hay không ?
- b) 6.x = 12 hay không ?
-
Học sinh tìm giá trị của x:
- Ở câu a, tìm được x = 4
- Ở câu b, không tìm được giá trị của x.
Nhận xét: ở câu a ta có phép chia hết: 12 : 3 = 4
Khái quát và ghi bảng:
-
- Cho hai số tự nhiên a và b (b≠0), nếu có số tự nhiên x sao cho b.x = a thì có phép chia hết a : b = x.
Hình thành khái niệm vectơ đối (tương tự khái niệm phép trừ, số đối)
Tình huống:
Cho
vectơ
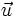 ,
xét
xem
có
vectơ
,
xét
xem
có
vectơ
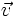 nào
mà
nào
mà
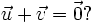
Với
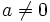 ,
nếu
,
nếu
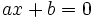 thì
thì
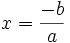 .
Thế
còn
.
Thế
còn
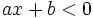 thì
thì
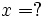
Tiếp cận công thức cộng lượng giác
| Hoạt động của GV | Hoạt động của HS |
|---|---|
|
Các
đẳng
thức
sau
đúng
hay
sai,
tại
sao?
a)
b)
|
Sai,
vì
a)
VT
=
VP
=
⇒ VT ≠ VP
b)
VT
=
VP
=
⇒ VT ≠ VP |
|
- Kết luận: Như vậy không được tính:
-
Vậy,
vấn
đề
đặt
ra
là
dùng
công
thức
nào
để
tính
được
|
- Công nhận, ghi nhớ - Tò mò |
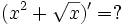
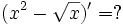
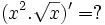
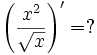

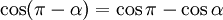
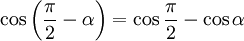
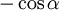 (công
thức
đã
có)
(công
thức
đã
có)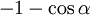
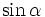
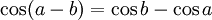
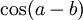 ?
?
