Hình học 10/Chương I/§3. Tích của vectơ với một số
Mục lục
Lí thuyết[sửa]
| Hoạt động 1 | |
Định nghĩa[sửa]
|
Cho
số
k
≠
0
và
vectơ
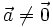 .
Tích
của
vectơ
.
Tích
của
vectơ
 với
số
k
là
một
vectơ:
với
số
k
là
một
vectơ:
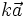 .
. |
|
Ta
quy
ước
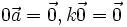 .
.
Người ta còn gọi tích của vectơ với một số là tích của một số với một vectơ.
| Hoạt động 2 | |
| VÍ DỤ 1 | |
NHẬN XÉT:
-
Với
một
vectơ
a
và
số
k
cho
trước,
ta
có
thể
vẽ
được
vô
số
vectơ
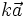 .
.
-
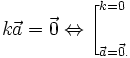
-
Vectơ
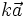 và
vectơ
và
vectơ
 luôn
cùng
phương
với
nhau.
luôn
cùng
phương
với
nhau.
Tính chất[sửa]
|
Với
hai
vectơ
 và
và
 bất
kì,
với
mọi
số
h
và
k,
ta
có:
bất
kì,
với
mọi
số
h
và
k,
ta
có:
|
|
| Hoạt động 3 | |
Trung điểm của đoạn thẳng và trọng tâm của tam giác[sửa]
a)
Nếu
I
là
trung
điểm
của
đoạn
thẳng
AB
thì
với
mọi
điểm
M
ta
có
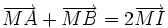 .
.
b)
Nếu
G
là
trọng
tâm
của
tam
giác
ABC
thì
với
mọi
điểm
M
ta
có
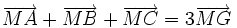 .
.
| Hoạt động 4 |
Hãy
sử
dụng
mục
5
của
§2
để
chứng
minh
các
khẳng
định
trên.
|
Điều kiện để hai vectơ cùng phương[sửa]
| Hoạt động 5 | |
Tổng quát, ta có:
-
-
Điều
kiện
cần
và
đủ
để
hai
vectơ
 và
và
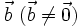 cùng
phương
là
có
một
số
k
để
cùng
phương
là
có
một
số
k
để
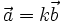 .
.
-
Điều
kiện
cần
và
đủ
để
hai
vectơ
CHỨNG MINH
-
Thuận:
giả
sử
 và
và
 cùng
phương.
cùng
phương.
-
Lấy
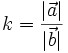 nếu
nếu
 và
và
 cùng
hướng
cùng
hướng -
Lấy
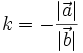 nếu
nếu
 và
và
 ngược
hướng.
ngược
hướng.
Khi
đó,
theo
định
nghĩa
ta
có
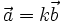 .
.
-
Đảo:
nếu
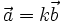 thì
hai
vectơ
thì
hai
vectơ
 và
và
 cùng
phương.
cùng
phương.
NHẬN
XÉT:
Ba
điểm
phân
biệt
A,
B,
C
thẳng
hàng
khi
và
chỉ
khi
có
số
k
khác
0
để
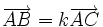 .
.
Phân tích một vectơ theo hai vectơ không cùng phương[sửa]
| Hoạt động 6 |
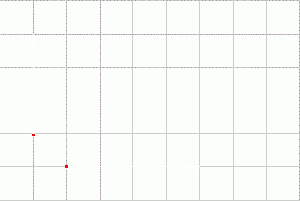
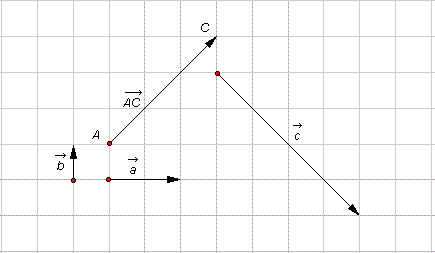
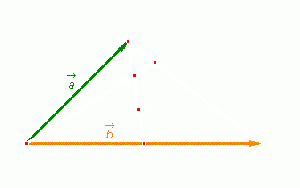
Cho
các
vectơ
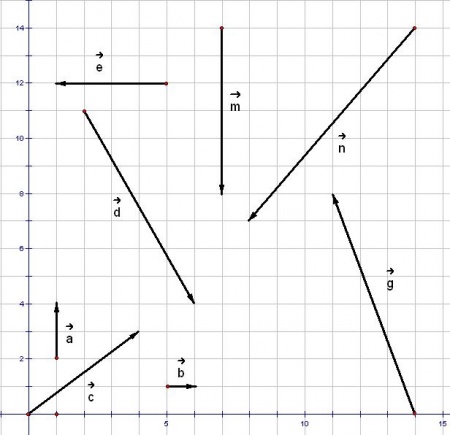
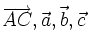 (hình
13p4).
(hình
13p4).
1)
Hãy
vẽ
vectơ
2)
Hãy
vẽ
vectơ
3)
Hãy
vẽ
vectơ
|
Tổng quát, ta có:
-
-
Cho
hai
vectơ
 và
và
 không
cùng
phương.
Khi
đó
mọi
vectơ
không
cùng
phương.
Khi
đó
mọi
vectơ
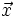 đều
phân
tích
được
một
cách
duy
nhất
theo
hai
vectơ
đều
phân
tích
được
một
cách
duy
nhất
theo
hai
vectơ
 và
và
 ,
nghĩa
là
có
duy
nhất
cặp
số
h,
k
sao
cho
,
nghĩa
là
có
duy
nhất
cặp
số
h,
k
sao
cho
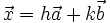 .
.
-
Cho
hai
vectơ
CHỨNG MINH
-
Vẽ
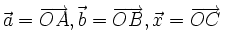 (hình
1-14).
(hình
1-14). - Kẻ CA' // OB và CB' // OA.
- Từ (2) suy ra, tứ giác OA'CB' là hình bình hành.
-
Từ
(3)
và
(1)
suy
ra,
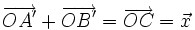 .
. -
Vì
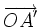 và
và
 cùng
phương
nên
có
một
số
h
để
cùng
phương
nên
có
một
số
h
để
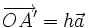 .
. -
Vì
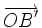 và
và
 cùng
phương
nên
có
một
số
k
để
cùng
phương
nên
có
một
số
k
để
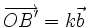 .
. -
Từ
(4),
(5)
và
(6)
suy
ra:
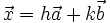 (đpcm).
(đpcm).
| VÍ DỤ 2 | |
| Lời giải |
a)
Gọi
AD
là
trung
tuyến
của
tam
giác
ABC
(hình
1-15).
Ta
có:
Do đó:
b)
Từ
(1*)
và
(2*),
ta
có
|
BÀI TẬP[sửa]
1)
Cho
hình
bình
hành
ABCD.
Chứng
minh
rằng:
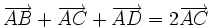 .
.
2)
Cho
các
vectơ
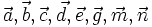 (hình
1-15p).
Tìm
k,
h
sao
cho:
(hình
1-15p).
Tìm
k,
h
sao
cho:
-
a)
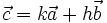
-
b)
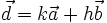
-
c)
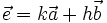
-
d)
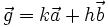
-
e)
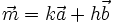
-
f)
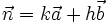
3)
Cho
AK
và
BM
là
hai
trung
tuyến
của
tam
giác
ABC.
Hãy
phân
tích
các
vectơ
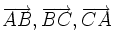 theo
hai
vectơ
theo
hai
vectơ
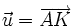 và
và
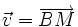 .
.
4)
Trên
đường
thẳng
chứa
cạnh
BC
của
tam
giác
ABC
lấy
một
điểm
M
sao
cho
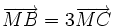 .
Hãy
phân
tích
vectơ
.
Hãy
phân
tích
vectơ
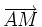 theo
hai
vectơ
theo
hai
vectơ
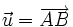 và
và
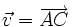 .
.
5) Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng:
-
a)
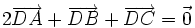 .
. -
b)
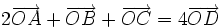 ,
với
O
là
điểm
tùy
ý.
,
với
O
là
điểm
tùy
ý.
6)
Gọi
M
và
N
lần
lượt
là
trung
điểm
các
cạnh
AB
và
CD
của
tứ
giác
ABCD.
Chứng
minh
rằng:
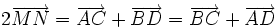 .
.
7)
Cho
hai
điểm
phân
biệt
A
và
B.
Tìm
điểm
K
sao
cho
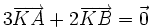
8)
Cho
tam
giác
ABC.
Tìm
điểm
M
sao
cho
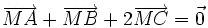 .
.
9) Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
10)
Cho
tam
giác
đều
ABC
có
O
là
trọng
tâm
và
M
là
một
điểm
tùy
ý
trong
tam
giác.
Gọi
D,
E,
F
lần
lượt
là
chân
đường
vuông
góc
hạ
từ
M
đến
BC,
AC,
AB.
Chứng
minh
rằng:
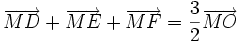 .
.



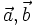 (hình
13p1).
(hình
13p1).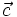 biết
biết
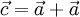 .
.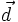 biết
biết
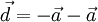 .
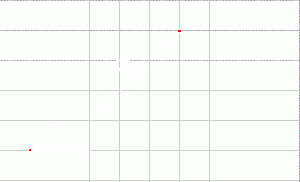
.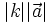 .
.
 và
vectơ
và
vectơ
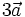 .
.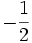 kí
hiệu
như
thế
nào?
Vẽ
vectơ
đó.
kí
hiệu
như
thế
nào?
Vẽ
vectơ
đó.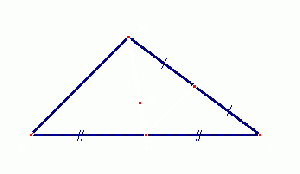
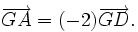
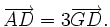
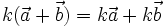
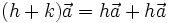
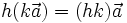
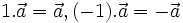
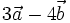 .
.
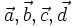 và
và
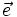 (hình
13p3).
Tìm
x,
y,
z
biết:
(hình
13p3).
Tìm
x,
y,
z
biết:
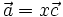
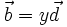
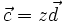 .
.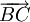 sao
cho
sao
cho
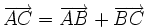 .
.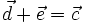 .
Có
bao
nhiêu
cặp
vectơ
.
Có
bao
nhiêu
cặp
vectơ
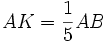 .
.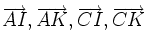 theo
theo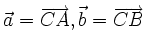 .
.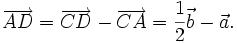
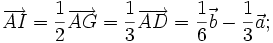
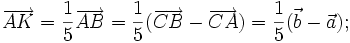
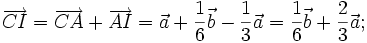 _____________(1*)
_____________(1*)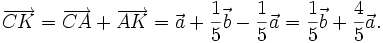 ___________(2*)
___________(2*)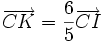 .
Vậy
ba
điểm
C,
I,
K
thẳng
hàng.
.
Vậy
ba
điểm
C,
I,
K
thẳng
hàng.