Đại số 10/Chương I/§4. Các tập hợp số
Mục lục
Lí thuyết[sửa]
Các tập hợp số đã học[sửa]
| Hoạt động 1 |
Vẽ
biểu
đồ
minh
họa
quan
hệ
bao
hàm
của
các
tập
hợp
số
đã
học.
|
Tập
hợp
các
số
tự
nhiên
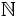
Tập
hợp
các
số
nguyên
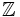
Các số -3, -2, -1,... là các số nguyên âm.
Tập
hợp
các
số
hữu
tỉ
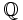
Ví
dụ:
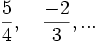
Số hữu tỉ có thể được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn. Chẳng hạn:
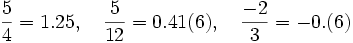
Tập
hợp
các
số
thực
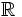
Tập hợp các số thực gồm các số thập phân hữu hạn, vô hạn tuần hoàn và vô hạn không tuần hoàn.
Các số thập phân vô hạn không tuần hoàn gọi là số vô tỉ.
Ví
dụ:
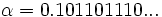 là
một
số
vô
tỉ
(với
số
chữ
số
1
sau
mỗi
chữ
số
0
tăng
dần).
là
một
số
vô
tỉ
(với
số
chữ
số
1
sau
mỗi
chữ
số
0
tăng
dần).
Ta cũng có thể nói rằng: Tập hợp các số thực gồm các số hữu tỉ và số vô tỉ.
Người ta thường dùng trục số để biểu diễn hình học các số, và ta đã biết:
Biểu diễn trên trục số giao của hai tập số[sửa]
Chúng ta đã biết cách biểu diễn một tập số trên trục số, bằng cách gạch đi các điểm (phần) không thuộc tập hợp đó, chẳng hạn:
-
Phần
không
bị
gạch
ở
hình
vẽ
sau
biễu
diễn
tập
hợp
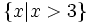
-
Phần
không
bị
gạch
ở
hình
vẽ
sau
biễu
diễn
tập
hợp
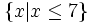
Đó
là
cách
biểu
diễn
một
tập
số
trên
trục
số.
Thế
còn,
muốn
biểu
diễn
giao
của
hai
tập
hợp
số
trên
trục
số
thì
ta
làm
thế
nào?
| Hoạt động 2 |
Biểu
diễn
tập
hợp
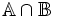 trên
trục
số:
trên
trục
số:
a)
Với
b)
Với
|
-
-
-
- CHÚ Ý
-
Từ
kết
quả
biểu
diễn
trên
trục
số
(hình
vẽ)
của
các
tập
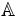 ,
,
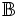 và
và
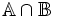 ,
"gợi"
cho
ta
cách
viết
các
tập
đó
"gọn
và
trực
quan
hơn".
Chẳng
hạn,
từ
câu
a):
,
"gợi"
cho
ta
cách
viết
các
tập
đó
"gọn
và
trực
quan
hơn".
Chẳng
hạn,
từ
câu
a):
-
Thay
vì
viết
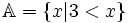 ta
có
thể
viết:
ta
có
thể
viết:
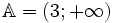
-
Thay
vì
viết
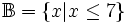 ta
có
thể
viết:
ta
có
thể
viết:
![{\mathbb {B}}=(-\infty ;7]](https://tusach.thuvienkhoahoc.com/images/math/f/6/1/f611e24d9ae2a3ab373fc428dd879812.png)
-
Thay
vì
viết
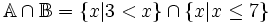 ta
có
thể
viết:
ta
có
thể
viết:
![{\mathbb {A}}\cap {\mathbb {B}}=(3;+\infty )\cap (-\infty ;7]](https://tusach.thuvienkhoahoc.com/images/math/3/0/0/300b32552410dd76a6ff5db106bc2ef8.png) .
.
-
Thay
vì
viết
- Như vậy, ta có:
-
-
![(3;+\infty )\cap (-\infty ;7]=(3;7]](https://tusach.thuvienkhoahoc.com/images/math/3/4/b/34b56ee57c64522de9b84bc65bf71a79.png)
Bằng
cách
biểu
diễn
và
"viết
gọn"
như
trên,
người
ta
quy
ước
cách
gọi,
kí
hiệu
và
biểu
diễn
trên
trục
số
một
vài
tập
số
thường
gặp
sau:
Các tập con thường dùng[sửa]
| Tên gọi và kí hiệu | Tính chất đặc trưng |
Biểu
diễn
trên
trục
số (phần không bị gạch) |
|---|---|---|
Khoảng
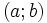
|
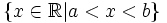 |
|
Khoảng
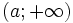
|
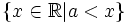 |
|
Khoảng
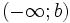
|
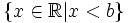 |
|
Khoảng
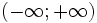
|
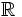 |
|
Đoạn
![[a;b]\,](https://tusach.thuvienkhoahoc.com/images/math/d/2/1/d21f69511ca60f3abd84c78449fef37c.png)
|
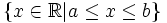 |
|
Nửa
khoảng
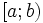
|
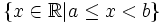 |
|
Nửa
khoảng
![(a;b]\,](https://tusach.thuvienkhoahoc.com/images/math/d/1/6/d161ecd904bdf1a65fa5fd503290b301.png)
|
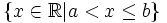 |
|
Nửa
khoảng
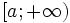
|
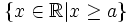 |
|
Nửa
khoảng
![(-\infty ;b]](https://tusach.thuvienkhoahoc.com/images/math/b/7/1/b7102cef4671d35a5db8eb06d10778b9.png)
|
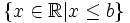 |
CHÚ Ý
- a và b được gọi là các đầu mút của đoạn, khoảng hay nửa khoảng.
-
Các
kí
hiệu
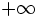 /
/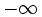 được
đọc
là
"dương
vô
cực"/"âm
vô
cực"
(hoặc
"dương
vô
cùng"/"âm
vô
cùng").
được
đọc
là
"dương
vô
cực"/"âm
vô
cực"
(hoặc
"dương
vô
cùng"/"âm
vô
cùng"). -
Toàn
bộ
tập
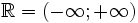 còn
được
gọi
là
đường
thẳng
thực.
còn
được
gọi
là
đường
thẳng
thực. -
Cách
đọc,
ví
dụ:
-
Kí
hiệu
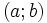 được
đọc
là
Khoảng
a
đến
b;
được
đọc
là
Khoảng
a
đến
b; -
Kí
hiệu
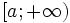 được
đọc
là
Nửa
khoảng
a
đến
dương
vô
cực.
được
đọc
là
Nửa
khoảng
a
đến
dương
vô
cực.
- (Các kí hiệu còn lại cũng được đọc tương tự)
-
Kí
hiệu
- Giống như viết phân số, từ nay trở đi khi kí hiệu một tập số ta nên viết nó dưới dạng "viết gọn".
| Hoạt động 3 | |
Biểu diễn trên trục số hợp của hai tập số[sửa]
Trên trục số, để biểu diễn hợp của hai tập số, ta cũng có thể dùng cách "gạch" đi các điểm (phần) không thuộc cả hai tập hợp (phần còn lại sẽ là hợp của hai tập đã cho).
Tuy nhiên, người ta thường sử dụng cách "đánh dấu", để tìm hợp của hai tập số.
-
- Trên trục số, lần lượt đánh dấu (tô đậm/khác màu) các điểm (phần) thuộc tập thứ nhất, thuộc tập thứ hai. Phần được đánh dấu sẽ biểu diễn hợp của hai tập số đã cho.
| VÍ DỤ |
Biểu
diễn
hợp
của
hai
tập
hợp
sau
trên
trục
số
và
sử
dụng
các
tập
con
thường
dùng
để
viết
gọn
chúng.
![[0;2)\cup (1;3]](https://tusach.thuvienkhoahoc.com/images/math/a/1/b/a1b730e99ed9f2b0bfd72a979d540f43.png) |
| Lời giải | |
BÀI TẬP[sửa]
| 1. Biểu diễn giao của các tập hợp sau trên trục số và sử dụng các tập con thường dùng để viết gọn chúng. | |
a)
![(-12;3]\cap [-1;4)](https://tusach.thuvienkhoahoc.com/images/math/2/a/0/2a0101032040b4888fc8d880c49823e5.png)
|
b)
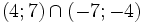
|
c)
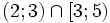
|
d)
![(-\infty ;2]\cap [-2;+\infty )](https://tusach.thuvienkhoahoc.com/images/math/1/1/2/11265656a3b99b35d0339c04a6205345.png)
|
| 2. Biểu diễn hiệu của các tập hợp sau trên trục số và sử dụng các tập con thường dùng để viết gọn chúng. | |
a)
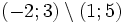
|
b)
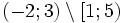
|
c)
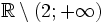
|
d)
![{\mathbb {R}}\setminus (-\infty ;3]](https://tusach.thuvienkhoahoc.com/images/math/c/4/d/c4d9748c7dc7d1bf900faf6f2991aa3d.png)
|
Hướng dẫn: Trên trục số, lần lượt:
- Gạch đi các điểm (phần) không thuộc tập thứ nhất.
- Gạch đi các điểm (phần) thuộc tập thứ hai.
| 3. Biểu diễn hợp của các tập hợp sau trên trục số và sử dụng các tập con thường dùng để viết gọn chúng. | |
a)
![[-3;1)\cup (0;4]](https://tusach.thuvienkhoahoc.com/images/math/0/4/2/042e7e706246ecfecd543114413817d0.png)
|
b)
![(0;2]\cup [-1;1)](https://tusach.thuvienkhoahoc.com/images/math/a/0/c/a0c4e89fefcc8d2066883a4bf2b91b60.png)
|
c)
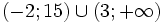
|
d)
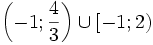
|
e)
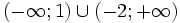
|
f)
![[-5;1]\cup (-3;2)](https://tusach.thuvienkhoahoc.com/images/math/e/f/b/efb62e91ad75a6dacc592e93d64945fb.png)
|
4.
Biểu
diễn
trên
trục
số
và
sử
dụng
các
tập
con
thường
dùng
để
viết
gọn
chúng.
a)
![(-\infty ;3]\cap (-2;+\infty )\cap \left[{\frac 12};+\infty \right)](https://tusach.thuvienkhoahoc.com/images/math/f/3/a/f3af679e0aad5224003a18144025778f.png)
b)
![(-3;5]\cup [8;10]\cup (2;8)](https://tusach.thuvienkhoahoc.com/images/math/a/6/4/a6432e8585a03670fa1f48c7161afe45.png)
c)
![(3;+\infty )\setminus (-\infty ;1]](https://tusach.thuvienkhoahoc.com/images/math/2/f/f/2ffabc991a96b229ea476e814df6e1ce.png)
Hướng dẫn: Giải như trường hợp giao/hợp của hai tập hợp.
| 5. Điền dấu "x" vào ô vuông thích hợp. | |||
a)
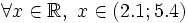
|
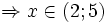 |
Đúng

|
Sai

|
b)
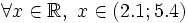
|
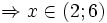 |
Đúng

|
Sai

|
c)
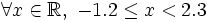
|
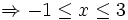 |
Đúng

|
Sai

|
d)
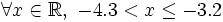
|
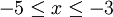 |
Đúng

|
Sai

|
e)
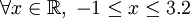
|
![x\in (-2;3.2]](https://tusach.thuvienkhoahoc.com/images/math/3/f/8/3f8efca109c347af0b2cc593f3b3ff45.png) |
Đúng

|
Sai

|
f)
![\forall x\in {\mathbb {R}},\ x\in (1;4.1]](https://tusach.thuvienkhoahoc.com/images/math/0/b/7/0b78e53a706998781834549386aae1bc.png)
|
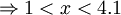 |
Đúng

|
Sai

|
Hướng dẫn: Biểu diễn các tập số trên trục số, từ đó suy ra.
6.
Biết
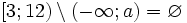
Có thể kết luận gì về giá trị của số a?
Xem thêm[sửa]
Tài liệu tham khảo[sửa]
-
Sách
in:
- Đại số 10, Nhà xuất bản Giáo dục, 2006, trang 16.
- Đại số 10 Nâng cao, Nhà xuất bản Giáo dục, 2006, trang 18.
- Đại số 10, Nhà xuất bản Giáo dục, 2001, trang 17.
- Tài liệu giáo khoa thí điểm, Đại số 10, Ban khoa học tự nhiên, Nhà xuất bản Giáo dục, 1997, trang 13.



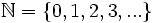
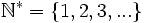
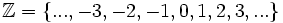
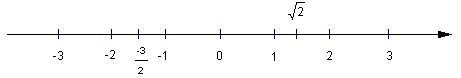
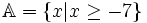 và
và
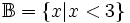




![x\in [1;3];](https://tusach.thuvienkhoahoc.com/images/math/d/a/e/dae7377679e4751d84ed76ce3f4c8a43.png)
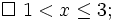

![x\in (1;3];](https://tusach.thuvienkhoahoc.com/images/math/c/1/5/c1588cbef8dac0d9484a41910f9e318e.png)
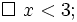
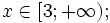
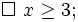
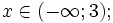
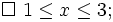
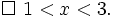
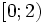 bằng
màu
xanh
(blue).
bằng
màu
xanh
(blue).
![(1;3]\,](https://tusach.thuvienkhoahoc.com/images/math/7/4/3/743bf8da5baa705b06779e04067abcbf.png) bằng
màu
đỏ
(red).
bằng
màu
đỏ
(red).
![[0;2)\cup (1;3]=[0;3]](https://tusach.thuvienkhoahoc.com/images/math/4/f/a/4fac99162b62443ab7b8e4110790727d.png)

