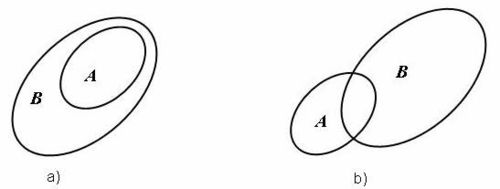Đại số 10/Chương I/§2. Tập hợp
Mục lục
Lí thuyết[sửa]
Khái niệm tập hợp[sửa]
Tập hợp và phần tử[sửa]
| Hoạt động 1 |
Nêu
ví
dụ
về
tập
hợp.
Dùng
các
kí
hiệu
a) 3 là một số nguyên tố
b)
|
|
Tập
hợp
(còn
gọi
là
tập)
là
một
khái
niệm
cơ
bản
của
toán
học,
không
định
nghĩa.
|
|
Giả
sử
đã
cho
tập
hợp
A.
-
-
Để
chỉ
a
là
một
phần
tử
của
tập
hợp
A,
ta
viết
a
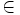 A
(đọc
là
a
thuộc
A).
A
(đọc
là
a
thuộc
A). -
Để
chỉ
a
không
phải
là
một
phần
tử
của
tập
hợp
A,
ta
viết
a
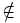 A
(đọc
là
a
không
thuộc
A).
A
(đọc
là
a
không
thuộc
A).
-
Để
chỉ
a
là
một
phần
tử
của
tập
hợp
A,
ta
viết
a
Cách xác định tập hợp[sửa]
| Hoạt động 2 |
Liệt
kê
các
phần
tử
của
tập
hợp
các
ước
nguyên
dương
của
30.
|
Khi liệt kê các phần tử của một tập hợp, ta viết các phần tử của nó trong hai dấu móc {... }, ví dụ A = {1, 2, 3, 5, 6, 10, 15, 30}.
| Hoạt động 3 |
Tập
hợp
B
các
nghiệm
của
phương
trình
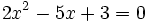 được
viết
là
được
viết
là
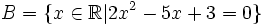 Hãy liệt kê các phần tử của tập hợp B. |
Một
tập
hợp
có
thể
được
xác
định
bằng
cách
chỉ
ra
tính
chất
đặc
trưng
cho
các
phần
tử
của
nó.
|
Một
tập
hợp
có
thể
xác
định
bằng
một
trong
hai
cách
sau:
|
|
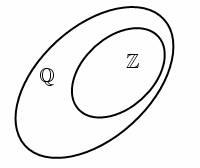
Người ta thường minh họa tập hợp bằng một hình phẳng được bao quanh bởi một đường kín, gọi là biểu đồ Ven như hình 1.
Tập hợp rỗng[sửa]
| Hoạt động 4 |
Hãy
liệt
kê
các
phần
tử
của
tập
hợp
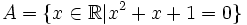 |
Phương
trình
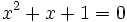 không
có
nghiệm.
Ta
nói
tập
hợp
các
nghiệm
của
phương
trình
này
là
tập
hợp
rỗng.
không
có
nghiệm.
Ta
nói
tập
hợp
các
nghiệm
của
phương
trình
này
là
tập
hợp
rỗng.
|
Tập
hợp
rỗng,
kí
hiệu
là
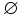 ,
là
tập
hợp
không
chứa
phần
tử
nào.
,
là
tập
hợp
không
chứa
phần
tử
nào. |
|
Nếu
A
không
phải
là
tập
hợp
rỗng
thì
A
chứa
ít
nhất
một
phần
tử:
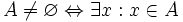
Tập hợp con[sửa]
| Hoạt động 5 | |
|
Nếu
mọi
phần
tử
của
tập
hợp
A
đều
là
phần
tử
của
tập
hợp
B
thì
ta
nói
A
là
một
tập
hợp
con
của
B
và
viết
A
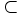 B
(đọc
là
A
chứa
trong
B).
B
(đọc
là
A
chứa
trong
B). |
|
Thay
cho
A
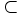 B,
ta
cũng
viết
B
B,
ta
cũng
viết
B
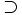 A
(đọc
là
B
chứa
A
hoặc
B
bao
hàm
A)
(hình
3.a).
Như
vậy
A
(đọc
là
B
chứa
A
hoặc
B
bao
hàm
A)
(hình
3.a).
Như
vậy
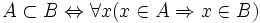
Nếu
A
không
phải
là
một
tập
hợp
con
của
B,
ta
viết
A
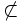 B.
(hình
3.b).
B.
(hình
3.b).
-
- Ta có các tính chất sau
-
a)
A
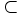 A
với
mọi
tập
hợp
A.
A
với
mọi
tập
hợp
A. -
b)
Nếu
A
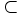 B
và
B
B
và
B
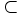 C
thì
A
C
thì
A
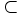 C
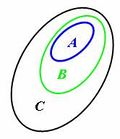
(hình
4)
C
(hình
4) -
c)
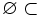 A
với
mọi
tập
hợp
A.
A
với
mọi
tập
hợp
A.
Tập hợp bằng nhau[sửa]
| Hoạt động 6 |
Xét
hai
tập
hợp
Hãy kiểm tra các kết luận sau:
a)
A
b)
B
|
|
Khi
A
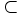 B
và
B
B
và
B
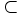 A
ta
nói
tập
hợp
A
bằng
tập
hợp
B
và
viết
A
=
B.
A
ta
nói
tập
hợp
A
bằng
tập
hợp
B
và
viết
A
=
B. |
|
Như
vậy
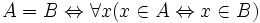
BÀI TẬP[sửa]
1.
Cho
A
=
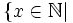 x
<
20
và
x
chia
hết
cho
3
x
<
20
và
x
chia
hết
cho
3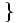 và
B
=
{2,
6,
12,
20,
30}
và
B
=
{2,
6,
12,
20,
30}
a) Hãy liệt kê các phần tử của tập hợp A.
b) Hãy xác định tập hợp B bằng cách chỉ ra một tính chất đặc trưng cho các phần tử của nó.
c) Hãy liệt kê các phần tử của tập hợp các học sinh lớp em cao dưới 1m60.
2.
Trong
hai
tập
hợp
A
và
B
dưới
đây,
tập
hợp
nào
là
tập
con
của
tập
hợp
còn
lại?
Hai
tập
A
và
B
có
bằng
nhau
không?
a) A là tập hợp các hình vuông
B là tập hợp các hình thoi.
b)
A
=
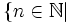 n
là
một
ước
chung
của
24
và
30
n
là
một
ước
chung
của
24
và
30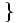
B
=
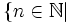 n
là
một
ước
của
6
n
là
một
ước
của
6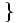
3.
Tìm
tất
cả
các
tập
con
của
tập
hợp
sau:
a) A = {a, b}
b) B = {0, 1, 2}
Tài liệu tham khảo[sửa]
Liên kết ngoài[sửa]
- Tập hợp trên My PC
- Bài giảng về Lý thuyết tập hợp ở Trường Đại học Cần Thơ
- Tập hợp trên Wikipedia
- Cơ bản về lý thuyết tập hợp
- Tập hợp trên MathWorld
- Notes on set theory



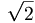 không
phải
là
một
số
hữu
tỉ.
không
phải
là
một
số
hữu
tỉ.
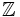 và
tập
hợp
các
số
hữu
tỉ
và
tập
hợp
các
số
hữu
tỉ
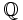 ?
Có
thể
nói
mỗi
số
nguyên
là
một
số
hữu
tỉ
hay
không?
?
Có
thể
nói
mỗi
số
nguyên
là
một
số
hữu
tỉ
hay
không?