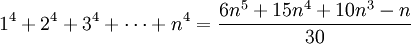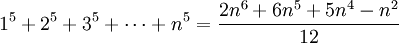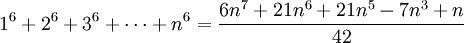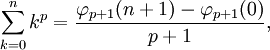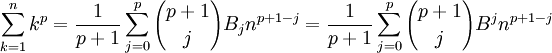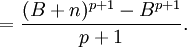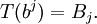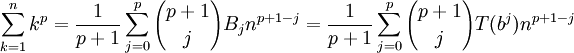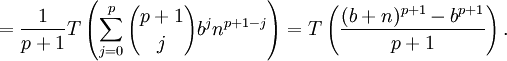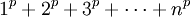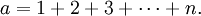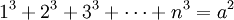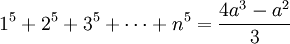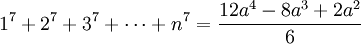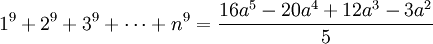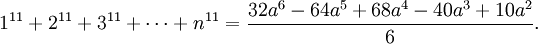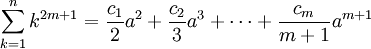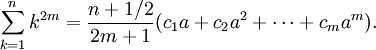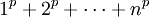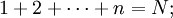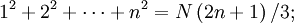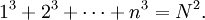Công thức Fauhaber
Công thức Faulhaber được đặt tên nhằm vinh danh nhà toán học Johann Faulhaber. Công thức đó biểu diễn tổng:
dưới dạng một đa thức bậc (p + 1) với biến n, và các hệ số liên quan đến số Bernoulli.
Công thức tổng quát:
Trong đó:
- chỉ số j có giới hạn trên là p, không phải là p + 1;
-
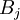 là
các
số
Bernoulli
là
các
số
Bernoulli
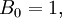
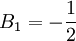 ,
hoặc
,
hoặc
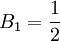 (tùy
vào
trường
hợp
cụ
thể),
(tùy
vào
trường
hợp
cụ
thể),
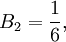
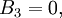
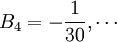
-
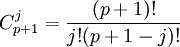 là
tổ
hợp
chập
j
của
(p+1),
còn
được
kí
hiệu
là
là
tổ
hợp
chập
j
của
(p+1),
còn
được
kí
hiệu
là
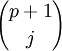 .
.
Ví
dụ:
p = 2,
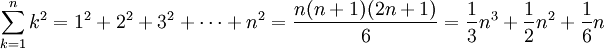 là
một
đa
thức
bậc
3
biến
n
và
các
hệ
số
là
một
đa
thức
bậc
3
biến
n
và
các
hệ
số
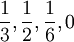
![\sum _{{k=1}}^{n}k^{2}={1 \over 3}.[(-1)^{0}.C_{{3}}^{0}.B_{0}.n^{{3-0}}+(-1)^{1}.C_{{3}}^{1}.B_{1}.n^{{3-1}}+(-1)^{2}.C_{{3}}^{2}.B_{2}.n^{{3-2}}+(-1)^{3}.C_{{3}}^{3}.B_{3}.n^{{3-3}}]={1 \over 3}n^{3}+{1 \over 2}n^{2}+{1 \over 6}n](https://tusach.thuvienkhoahoc.com/images/math/d/f/0/df076e64575acd4849a9009c1d9f536b.png) .
.
Bản
thân
Faulhaber
không
biết
công
thức
tổng
quát
trên,
ông
chỉ
tính
tổng :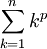 với
17
giá
trị
đầu
tiên
của
p,
và
rút
ra
một
số
nhận
xét.
Mãi
sau
này,
công
thức
tổng
quát
mới
được
tìm
ra
khi
người
ta
đã
biết
đến
số
Bernoulli.[1]
với
17
giá
trị
đầu
tiên
của
p,
và
rút
ra
một
số
nhận
xét.
Mãi
sau
này,
công
thức
tổng
quát
mới
được
tìm
ra
khi
người
ta
đã
biết
đến
số
Bernoulli.[1]
Mục lục
Ví dụ[sửa]
-
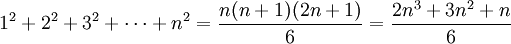 (số
hình
chóp
vuông
(tiếng
Anh
là
square
pyramidal
number))
(số
hình
chóp
vuông
(tiếng
Anh
là
square
pyramidal
number)) -
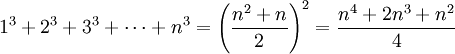 (số
tam
giác
vuông
(tiếng
Anh
là
squared
triangular
number))
(số
tam
giác
vuông
(tiếng
Anh
là
squared
triangular
number))
Liên hệ với đa thức Bernoulli[sửa]
Công thức tổng quát cũng có thể được viết dưới dạng:
với φj là đa thức Bernoulli bậcj.
Umbral form[sửa]
|
Bài
này
đang
được
dịch
từ
ngôn
ngữ
khác. Nếu bạn có đủ khả năng xin góp sức dịch bài này. Nếu không tiếp tục được quan tâm, phần ngoại ngữ của bài sẽ bị xóa sau khoảng 1 tháng. Xin đừng quên chuyển các mục Chú thích, Tham khảo vào bài dịch để đáp ứng tiêu chuẩn. Xin tham khảo Hướng dẫn cách biên soạn bài để biết thêm chi tiết. |
Lỗi biểu thức: Dấu phân cách “[” không rõ ràng
In
the
classic
umbral
calculus
one
formally
treats
the
indices
j
in
a
sequence
Bj
as
if
they
were
exponents,
so
that,
in
this
case
we
can
apply
the
binomial
theorem
and
say
In the modern umbral calculus, one considers the linear functional T on the vector space of polynomials in a variable b given by
Then one can say
Đa thức Faulhaber[sửa]
Một số tác giả sử dụng thuật ngữ đa thức Faulhaber để chỉ một dạng đa thức tổng quát khác. Bản thân Faulhaber nhận xét rằng, nếu p lẻ thì tổng:
là đa thức với biến là
Ví dụ:
Trường hợp p = 3, còn được biết đến với tên gọi Định lý Nicomachus.
Các đa thức ở vế phải còn được gọi là đa thức Faulhaber với biến a. Chúng đều chia được cho a 2 bởi vì với j > 1 lẻ thì số Bernoulli Bj bằng 0.
Faulhaber đã biết rằng với bậc p lẻ, nếu tổng được viết dưới dạng:
thì với bậc p chẵn tổng sẽ có dạng:
Vì a = n(n + 1)/2, nên với bậc p lẻ (lớn hơn 1), tổng là 1 đa-thức biến n có-chứa các nhân tử n2 and (n + 1)2, còn nếu p chẵn thì tổng sẽ là đa thức có chứa nhân tử n, n + ½ và n + 1.
Công thức Faulhaber có thể gặp trong tự nhiên. Ví dụ, số hiệu nguyên tử của các nguyên tố hóa học thuộc nhóm kim loại kiềm thổ (Be, Ca, Ba) thỏa-mãn công-thức (4/3)n(n + 1/2)(n + 1), với n là số thứ tự của các kim loại này trong nhóm.
Lịch sử[sửa]
Công thức Faulhaber còn có tên gọi khác là công thức Bernoulli. Bản thân Faulhaber không biết công thức ở dạng tổng quát. Ông chỉ tính tổng với 17 giá trị đầu tiên của bậc p, và rút ra một vài tính chất của dạng tổng quát. [2]
Faulhaber nhận ra rằng với bậc p lẻ,
là đa thức không chỉ với biến n mà còn nhận số tam giác N = n(n + 1)/2 làm biến. Ví dụ, ông nhận xét:
Những công thức trên chỉ là nhận xét của Faulhaber rút ra khi nghiên cứu các giá trị cụ thể của p. Chứng minh chặt chẽ cho các công thức đó với mọi bậc p lẻ mãi đến năm 1834 mới được đưa ra bởi nhà toán học Carl Jacobi
Liên kết ngoài[sửa]
Lỗi
chú
thích:
Tồn
tại
thẻ
<ref>,
nhưng
không
tìm
thấy
thẻ
<references/>
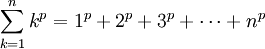
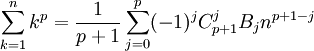
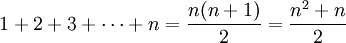 (
(