Sách:Điện từ sinh học/Cắt lớp trở kháng
26.1 LỜI GIỚI THIỆU.
Trong chương trước, phép đo biến đổi thể tích dựa trên trở kháng đã được thảo luận, tín hiệu trở kháng là tín hiệu đơn phát hiện giữa một cặp điện cực. Vì vậy, nó là trở kháng trung bình của vùng giữa những điện cực đó, kết quả được xác định bởi những điểm giữa trường đạo trình của các điện cực đo và dòng cung cấp cho các điện cực.
Độ phân giải không gian của phép đo trở kháng có thể được nâng cao bằng cách sử dụng một mảng điện cực xung quanh vật dẫn khối cần quan tâm. Dòng điện có thể được cung cấp liên tiếp qua các cặp điện cực khác nhau và điện áp tương ứng được đo liên tiếp bởi tất cả các cặp điện cực còn lại. Bằng cách này có thể sử dụng thuật toán tái tạo để tạo một hình ảnh trở kháng của những vùng khác nhau của vật dẫn khối. Phương pháp này được gọi là tạo ảnh trở kháng. Vì hình ảnh hai chiều này thường được tái tạo từ một lát cắt của vật dẫn khối, nên phương pháp này cũng được gọi là Cắt lớp trở kháng hay ECCT (electric current computed tomography). Vì vậy cắt lớp trở kháng là một phương pháp tạo ảnh có thể trợ giúp Cắt lớp điện toán (computer tomography, CT), tạo ảnh siêu âm, chụp cắt lớp phát xạ positron, v.v. Người đọc có thể được nhiều thông tin về những phương pháp tạo ảnh y tế hiện đại từ những tài liệu tham khảo như Krestel (1990) , Webb ( 1992 ) và Wells (1982).
Trong việc tạo ảnh, người ta mong muốn giới hạn được vùng, và biết dạng hình học của vùng này. Nói chung, điều này chỉ biết được một cách chính xác nếu tín hiệu năng lượng tiến hành tuyến tính. Điều kiện này thỏa mãn đối với tia X và phóng xạ hạt nhân. Nó cũng đúng trong kỹ thuật chụp ảnh thông thường với điều kiện thêm là các tia sáng bẻ cong trong thấu kính theo một cách đã được biết chính xác. Nếu năng lượng bức xạ tiến hành không rõ đường dẫn, hoặc nếu nó đi từ nguồn tới đích thông qua một số đường (ví dụ, qua một thể tích lớn), thì sẽ không thể để tạo ra một ảnh chính xác. Như các ví dụ về điều này trong nhiếp ảnh (hoặc tầm nhìn), ta có thể đề cập đến vầng hào quang xung quanh mặt trời hay ảnh ảo.
Trong cắt lớp trở kháng, vấn đề cơ bản trong tái tạo ảnh, trong một trường hợp nói chung, là dòng điện không thể bị ép chảy một cách tuyến tính (hoặc thậm chí trong một đường đã biết) trong một vật dẫn khối không đồng nhất. Khi không có nguồn ở trong vật dẫn khối ( các nguồn nằm trên bề mặt bao trong dạng của dòng đưa vào ), do vậy trường điện thế Φ phải thỏa mãn (σ Φ) = 0 và chỉ một lớp chức năng giới hạn có thể đáp ứng điều này. Trong đó σ là hằng số, khi đó Φ thỏa mãn phương trình Laplace và vì vậy những dạng chức năng ít hơn cũng có giá trị (như đa thức Legendre, …). Như đã nói trong mục 11.6.9, nó có thể tạo trường dòng tuyến tính trong một vật dẫn khối đồng nhất có hình dạng tùy ý. Trong ý nghĩa của cắt lớp trở kháng một vật dẫn khối là của vùng quan tâm nhỏ, bởi vì ảnh của nó chiếm 50% là màu xám (tức là đồng nhất).
Tuy nhiên tính chính xác của những hình ảnh này không bị giới hạn bởi kích cỡ các điện cực, mà bởi kích cỡ tiêu điểm của ống tia X và detector trong máy cắt lớp điện toán. Trong tạo ảnh trở kháng, hình ảnh bị làm mờ bởi vì trong một vật dẫn khối đường đi của dòng điện là không tuyến tính và nói chung là không biết được chính xác.
Cần lưu ý rằng, mặc dù mục đích cơ bản của cắt lớp trở kháng là tái tạo một ảnh trở kháng từ một lát cắt của một vùng 3 chiều của cơ thể, nó cũng có thể được dùng để kiểm tra một cách chính xác hơn một vài thông số sinh lý học. Woo, Hua, và Webster (1992) đã trình bày một ví dụ về loại thiết bị kiểm tra trẻ sơ sinh ngạt thở đáng tin cậy hơn. Với kỹ thuật cắt lớp trở kháng, có thể tập trung vào việc thu thập các dữ liệu trở kháng chính xác hơn tới vùng phổi và vì vậy tránh được nhiễu gây ra bởi sự chuyển động của thành ngực.
Trong chương này chúng ta sẽ xem lại ngắn gọn vài câu hỏi cơ bản trong cắt lớp trở kháng. Người đọc có thể thu được nhiều thông tin hơn từ những nguồn xuất sắc như Brown and Barber (1992), Hames (1990), và Webster (1990).
26.2 NHỮNG PHƯƠNG PHÁP ĐO TRỞ KHÁNG.
Trở kháng điện có thể được đo truyền thống bằng phương pháp hoàn toàn dòng điện hoặc bằng phương pháp điện từ. Phương pháp điện từ truyền thống được thảo luận đầu tiên.
26.2.1 Phép đo điện của trở kháng.
Như trong phép đo biến đổi thể tích dựa trên trở kháng, cũng có trong cắt lớp trở kháng, dòng được cung cấp và điện áp được đo thông qua những cặp điện cực khác nhau để tránh những lỗi dựa vào trở kháng liên hệ. Tuy nhiên chúng ta cần lưu ý, những điều khẳng định của Cheng et al (1990) rằng, mặc dù vấn đề của điện trở da, để có được độ nhạy lớn nhất đối với các thay đổi trong điện trở suất của cơ thể, cần có điện áp từ điện cực mang dòng. Phần sau đây đề cập một số phương pháp đo lường được sử dụng.
Phương pháp lân cận (Neighboring Method).
Brown và Segar (1987) đã đề xuất một phương pháp mà dòng được đưa vào qua các điện cực lân cận và điện áp được đo liên tiếp từ tất cả các cặp điện cực liền kề khác. Hình 26.1 minh họa việc ứng dụng của phương pháp này cho một vật dẫn khối hình trụ với 16 điện cực đặt cách đều nhau.
Dòng được đầu tiên đưa vào qua điện cực 1 và 2 (hình 26.1A). Mật độ dòng là cao nhất giữa các điện cực này, giảm nhanh chóng như là hàm số của khoảng cách. Điện áp được đo đều đặn liên tục giữa các cặp điện cực 3-4, 4-5, … 15-16. Bốn phép đo đầu tiên trong 13 phép đo được minh họa trong hình 26.1A. Tất cả 13 phép đo là độc lập. Mỗi trong số chúng được giả định để miêu tả trở kháng giữa phép đo những điện cực dòng đẳng thế giao nhau. Điều này cho biết sự hơi khác nhau của phép đo điện áp giữa điện cực 6 và 7.
(Nghiên cứu sau của Kauppinen, Hyttinen, và Malmivuo (2006) đã chỉ ra rằng những giả định này là không đúng).
Sự
thiết
lập
tiếp
theo
của
13
phép
đo
điện
áp
thu
được
bởi
cung
cấp
dòng
qua
điện
cực
2
và
3,
như
đã
thể
hiện
trong
hình
26.1B.
Đối
với
hệ
thống
16
điện
cực,
sẽ
thu
được
16x13=208
phép
đo
điện
áp.
Do
có
sự
qua
lại,
dòng
và
áp
những
điện
cực
trong
những
phép
đo
đó
được
trao
đổi
mang
lại
những
kết
quả
khác
nhau.
Vì
vậy,
chỉ
có
104
phép
đo
độc
lập.
Trong
phương
pháp
lân
cận,
điện
áp
thu
được
là
lớn
nhất
với
những
cặp
điện
cực
liền
kề.
Với
những
cặp
điện
cực
đối
diện,
điện
áp
chỉ
khoảng
2.5%.
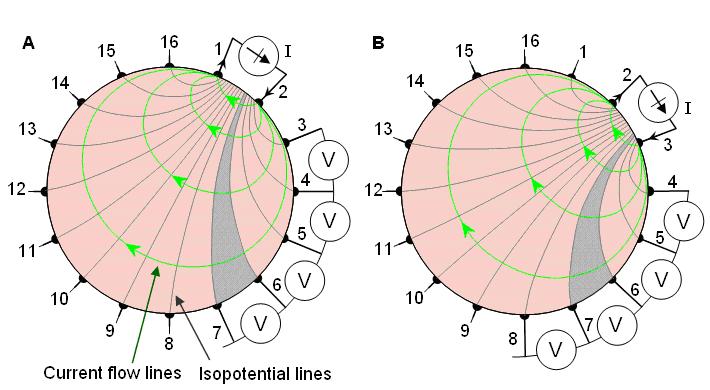
Hình 26.1 Phương pháp lân cận của dữ liệu trở kháng thu được được minh họa bởi một vật dẫn hình trụ và 16 điện cực đặt cách đều nhau.
(A) Bốn phép đo điện áp đầu tiên trong sự thiết lập 13 phép đo
(B) Sự thiết lập khác của 13 phép đo thu được bởi thay đổi dòng cung cấp cho các điện cực.
Phương pháp Cross
Một phân bố dòng đồng bộ hơn thu được khi dòng được tiêm giữa một cặp điện cực cách xa hơn. Hua, Webster, và Tompkins (1987) đã đề xuất phương pháp Cross (như hình 26.2).
Trong phương pháp Cross, những điện cực liền kề, ví dụ như 16 và 1, được thể hiện trong hình 26.2A, được lựa chọn đầu tiên cho dòng và điện áp tham chiếu những điện cực, tương ứng. Dòng điện cực khác, điện cực số 2 được sử dụng đầu tiên. Điện áp được đo liên tiếp cho tất cả 13 điện cực khác với điện cực 1 đã nói ở trên như là một sự tham chiếu. (Bốn phép đo điện áp đầu tiên được thể hiện một lần nữa trong hình 26.2A). Dòng sau đó được đưa qua điện cực 4 và điện áp lại được đo liên tiếp cho tất cả 13 điện cực khác với điện cực 1 như là sự tham chiếu, được thể hiện trong hình 26.2B. Quá trình được lặp lại khi dùng những điện cực 6, 8,…14; toàn bộ quá trình bao gồm 7x13=91 phép đo.
Chuỗi
phép
đo
sau
đó
được
lặp
lại
dùng
điện
cực
3
và
2
như
dòng
và
điện
áp
tham
chiếu
điện
cực,
tương
ứng
(nhìn
hình
26.2C).
Đưa
dòng
đầu
tiên
tới
điện
cực
5,
sau
đó
đo
điện
áp
liên
tiếp
cho
13
điện
cực
khác
với
điện
cực
2
như
là
một
sự
tham
chiếu.
Lặp
lại
quá
trình
bằng
cách
đưa
dòng
tới
điện
cực
7
(nhìn
hình
26.2D).
Đưa
dòng
liên
tiếp
tới
các
điện
cực
9,
11,…,1
và
đo
điện
áp
cho
tất
cả
13
điện
cực
khác
với
điện
cực
2
đã
nói
ở
trên
như
một
sự
tham
chiếu,
mỗi
lần
tạo
91
phép
đo.
Từ
182
phép
đo
này
chỉ
có
104
phép
đo
độc
lập.
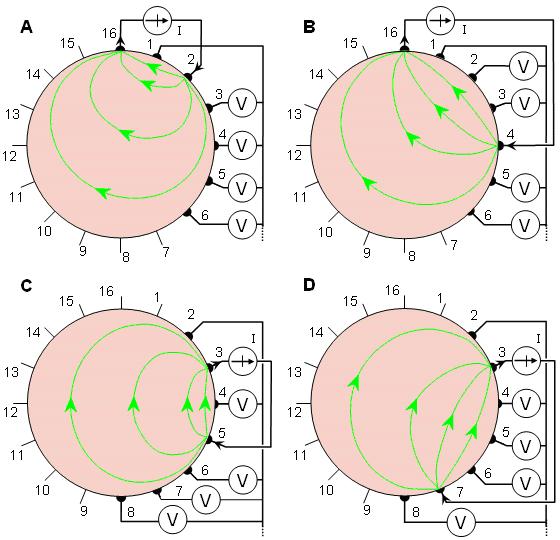
Hình 26.2 Phương pháp Cross của dữ liệu trở kháng thu được. Bốn bước khác nhau của quá trình này được minh họa từ A đến D.
Phương pháp đối lập (Opposite Method).
Phép đo trở kháng tương tự khác là phương pháp đối lập, được minh họa trong hình 26.3 (Hua, Webster, and Tompkins, 1987). Trong phương pháp này dòng được tiêm qua hai điện cực hoàn toàn đối diện (điện cực 16 và 8 trong hình 26.3A). Điện cực liền kề điện cực được tiêm dòng được dùng như điện áp tham chiếu. Điện áp được đo từ tất cả những điện cực khác trừ những điện cực dòng, gồm 13 phép đo điện áp (bốn phép đo đầu tiên đã được trình bày lại).
Sự
thiết
lập
của
13
phép
đo
điện
áp
tiếp
theo
thu
được
bằng
cách
chọn
điện
cực
1
và
9
làm
điện
cực
dòng
(hình
26.3B).
Khi
16
điện
cực
được
sử
dụng,
phương
pháp
đối
diện
có
8x13=104
điểm
dữ
liệu.
Sự
phân
bố
dòng
trong
phương
pháp
này
đồng
đều
hơn
và
vì
vậy
có
độ
nhạy
tốt
hơn.
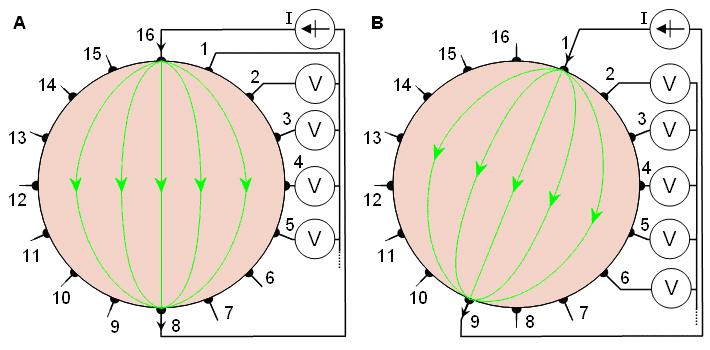
Hình
26.3A
Phương
pháp
đối
diện
của
dữ
liệu
trở
kháng
thu
được.
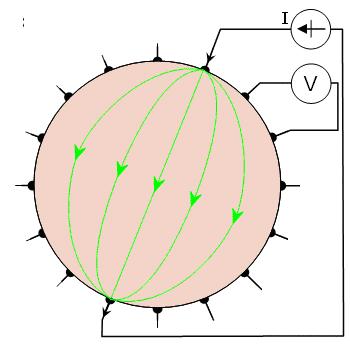
Hình 26.3B Sự thực hiện của phương pháp đối diện.
Phương pháp thích ứng (Adaptive Method).
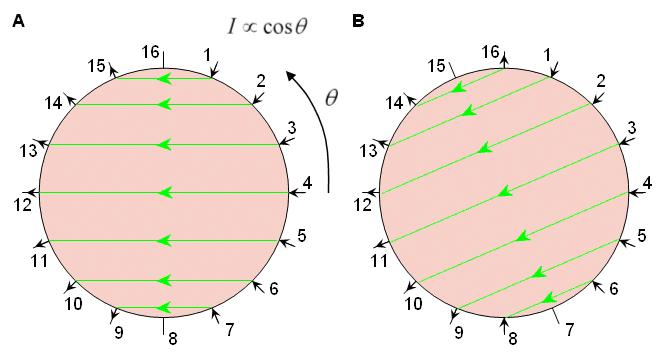
Trong những phương pháp đã nói ở trên, dòng được tiêm với một cặp điện cực và điện áp được đo tương tự nhau. Trong phương pháp thích ứng, được đề xuất bởi Gisser, Isaacson, và Newell (1987), dòng được tiêm qua tất cả các điện cực (nhìn hình 26.4A). Do dòng qua tất cả các điện cực đồng thời, nên nhiều bộ tạo dòng độc lập được cần như là các điện cực được sử dụng. Điện cực có thể cung cấp một dòng từ -5 đến +5mA, khiến sự phân bố dòng khác nhau. Sự phân bố dòng đồng nhất có thể chỉ thu được trong vật dẫn khối đồng nhất, như đã thảo luận trong phần 11.6.9. Nếu vật dẫn khối là hình trụ với lát cắt tròn, dòng tiêm phải tỉ lệ với cosθ để thu được một phân bố dòng đồng nhất.
Lưu ý, điện áp được đo với sự nối đất các điện cực riêng biệt. Mỗi lần đo dùng 16 điện cực, số phép đo điện áp của một phân bố dòng không đổi là 15. Phân bố dòng đòi hỏi là khi quay một điện cực tăng dần (22.5 cho hệ thống 16 điện cực, nhìn hình 26.4B). Vì vậy thu được 8 phân bố dòng khác nhau, gồm 8x15=120 phép đo điện áp độc lập.
 Hình
26.4
Phương
pháp
thích
ứng
của
dữ
liệu
trở
kháng
thu
được.
Hình
26.4
Phương
pháp
thích
ứng
của
dữ
liệu
trở
kháng
thu
được.
26.2.2 Phép đo điện từ của trở kháng điện.
Đầu chương, ưu tiên thảo luận phép đo biến đổi thể tích dựa trên trở kháng, trở kháng điện được đo bởi sự cung cấp một dòng điện tới vật dẫn khối của cơ thể và đo điện thế điện khác nhau được phát ra (như điện áp). Như đã thảo luận trong phụ lục B, phương trrình Maxwell's kết hợp sự biến đổi giữa điện trường và từ trường để chỉ rõ khi có một điện trường thì cũng có một từ trường và ngược lại. Như đã đề cập trong phần giới thiệu mục 1.2.1, sự kết hợp điện từ trường có thể được dùng để đo trở kháng điện.
Trong phép đo điện từ của trở kháng điện, giống trong phép đo hoàn toàn điện, sự phân bố độ nhạy của phép đo tỉ lệ với số điểm giữa điện trường trong vật dẫn khối và trường đạo trình của phép đo điện áp. Giá trị đúng ko kể có hay không dòng điện trong vật dẫn khối được tạo ra thông qua ứng dụng trực tiếp của dòng điện hoặc được cảm ứng bởi một trường từ biến thiên theo thời gian không kể bộ dò là một từ kế hay một vôn kế, tương ứng. Trong hình 1.2B nguyên lý phép đo điện từ của trở kháng điện được giới thiệu ngắn gọn, chúng được trình bày nhiều hơn ở dưới.
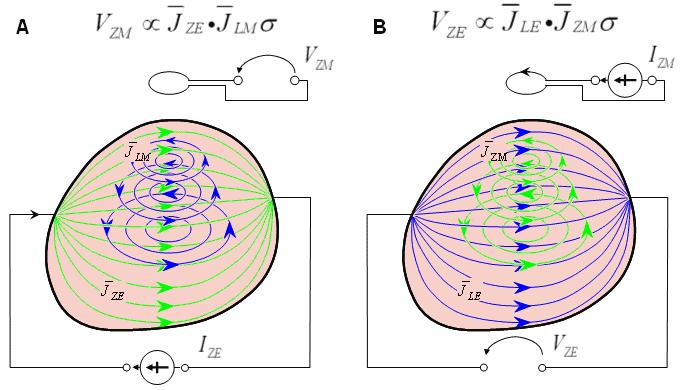
Một cách để sử dụng sự kết hợp điện từ trường trong phép đo trở kháng điện là cung cấp dòng điện tới vật dẫn khối gián tiếp qua các điện cực trên bề mặt của nó, thay vì nhận ra điện áp phát tới các cặp điện cực khác, từ trường cảm ứng được phát hiện với một từ kế. Trong phương pháp này, sự phân bố dòng điện là không xoắn (zero curl). Như đã thảo luận trong chương 12, trường đạo trình của từ kế là tiếp xúc được định hướng. Phép chiếu lại cho hình ảnh trở kháng được tạo bằng cách đầu tiên xác định sự phân bố dòng điện trong vật dẫn khối từ phép đo từ trường và sau đó phân bố trở kháng. Hình 26.5A minh họa nguyên lý này. Hình ảnh trở kháng thu được với phương pháp này không được công bố. Ahlfors và Ilmoniemi (1992) đã công bố sự thay đổi điện trường do một ống trụ đặt cách ly đặt tại một bình chứa nước muối, được đo lường với một máy đo từ SQUID 24 kênh.
Sự kết hợp điện từ trường cũng có thể được dùng theo nhiều cách khác trong phép đo trở kháng điện của vật dẫn khối. Do sự kết hợp điện từ trường, dòng điện có thể cũng được cảm ứng bởi một từ trường biến thiên theo thời gian phát ra bởi một vòng hoặc hệ thống vòng xung quanh vật dẫn khối (Purvis, Tozer, and Freeston, 1990). Điều này đem đến cơ hội tạo nhiều loại phân bố dòng khác nhau so với sự cung cấp dòng điện qua các điện cực. Trong trường hợp này, trường dòng điện có từ tính (zero divergence). Nguyên lý của phép đo trở kháng điện này được minh họa trong hình 26.5B. Healey, Tozer, và Freeston (1992) đã công bố ảnh trở kháng đo được từ một phantom 3 chiều. Chúng ta dùng 3 vòng cách đều nhau quanh một phantom hình trụ và đo điện thế bởi 16 điện cực đặt cách đều trên bề mặt.
Chú ý rằng vì sự phân bố độ nhạy của phép đo điện từ trở kháng điện tỉ lệ với số điểm trong điện trường và detector trường đạo trình, ở cả hai dạng này, do nguyên lý sự qua lại, phân bố độ nhạy là giống nhau, với điều kiện là vòng và cấu trúc điện cực dùng là giống nhau.
 Hình
26.5
Phương
pháp
điện
từ
của
dữ
liệu
trở
kháng
thu
được.
Hình
26.5
Phương
pháp
điện
từ
của
dữ
liệu
trở
kháng
thu
được.
(A)Dòng điện được cung cấp qua các điện cực, và sự phân bố dòng được phát hiện với một từ kế.
(B) Dòng điện được cảm ứng với một vòng, và điện áp cảm ứng được đo với các điện cực.
26.3 TÁI TẠO HÌNH ẢNH.
Từ việc thu thập dữ liệu, phân bố hình ảnh của trở kháng điện có thể được xây dựng lại bằng cách dùng thuật toán tái tạo hình ảnh. Những thuật toán này được thảo luận ở nhiều chi tiết trong Webster (1990) và không nhắc lại ở đây. Độ chính xác cao nhất của tái tạo ảnh thu được hiện nay khoảng 5% kích thước vật dẫn khối trong mẫu kiểm tra, và khoảng 10% trong phép đo cơ thể sống ở ngực. Độ phân giải cuối cùng có thể đạt được là 1.5% được công bố bởi Barber và Brown (1984). Với sự nghiên cứu não, phương pháp trở kháng không được áp dụng vì bộ não có độ nhạy rất cao. Sự phân biệt trong hình ảnh trở kháng là lý thuyết thảo luận trong Cheney và Isaacson (1992).
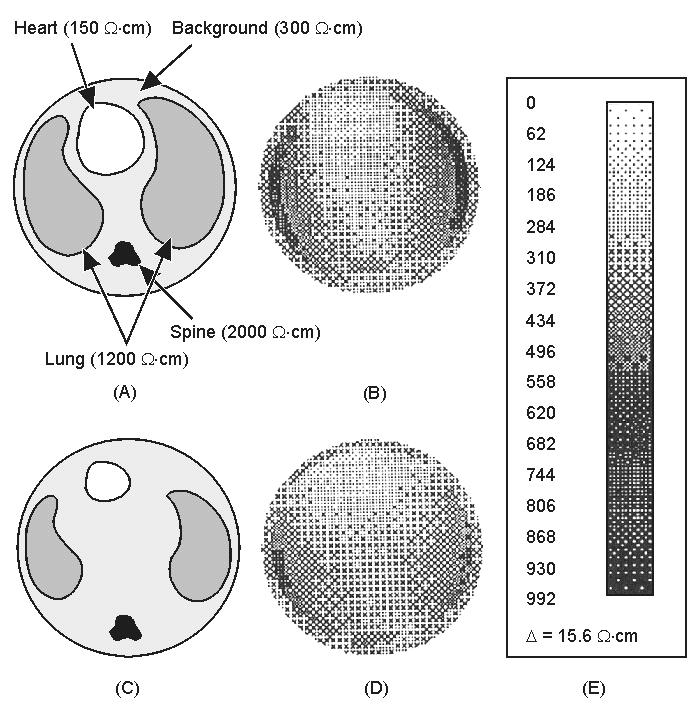
Một ví dụ tái tạo hình ảnh được trình bày trong hình 26.6 (Woo, 1990). Trong thí nghiệm này, ảnh trở kháng được xác định từ hai phatoms khác nhau tương tự như lát cắt ngang của cơ thể người. Phantoms được chế tạo bởi sự trộn bột agar và NaCl với nước sôi. Hình 26.6A và C chỉ rõ hình ảnh đúng của hai phantoms. Sự tái tạo hình ảnh trở kháng của những phantoms này được thể hiện trong phần B và D, tương ứng. Hình 26.6E minh họa mức điện trở suất của hình ảnh.
Như một phương thức không ion hóa, rẻ, cắt lớp trở kháng điện là một phụ lục cần quan tâm tới những phương pháp ảnh y tế khác nhau. Dù độ phân giải hình ảnh khi nghiên cứu trong cơ thể sống liên tục tăng, về lý thuyết, nó sẽ vẫn còn thấp hơn của X-quang và siêu âm. Độ phân giải thấp này tất nhiên sẽ giới hạn ứng dụng của chúng tới các máy theo dõi, đúng hơn là sự ứng dụng chính xác hình ảnh giải phẫu.
 Hình
26.6
Ví
dụ
về
tái
tạo
hình
ảnh
cắt
lớp
trở
kháng
trong
phantom.
Hình
26.6
Ví
dụ
về
tái
tạo
hình
ảnh
cắt
lớp
trở
kháng
trong
phantom.
(A) và (C) Hình ảnh đúng của phantom tạo mẫu ngực cơ thể.
(B) và (D) Tái tạo hình ảnh của A và C, tương ứng.
(E) Mức điện trở suất hình ảnh.
TÀI LIỆU THAM KHẢO
Ahlfors S, Ilmoniemi R (1992): Magnetic imaging of conductivity. In Proc. 14th Annual Int. Conf. IEEE Eng. In Med. And Biol. Society, Paris, Vol. 14, ed. JP Morucci, R Plonsey, JL Coatrieux, S Laxminarayan, pp. 1717-8, IEEE, Piscatway, N.J.
Barber DC, Brown BH (1984): Applied potential tomography. J. Phys. E.: Sci. Instrum. 17: 723-33.
Brown BH, Segar AD (1987): The Sheffield data collection system. Clin. Phys. Physiol. Measurement 8(Suppl. A): 91-7.
Cheney M, Isaacson D (1992): Distinguishability in impedance imaging. IEEE Trans. Biomed. Eng. 39:(8) 852-60.
Cheng KS, Simske SJ, Isaacson D, Newell JC, Gisser DG (1990): Errors due to measuring voltage on current-carrying electrodes in electric current computed tomography. IEEE Trans. Biomed. Eng. 37:(60) 60-5.
Gisser DG, Isaacson D, Newell JC (1987): Current topics in impedance imaging. Clin. Phys. Physiol. Measurement 8(Suppl. A): 39-46.
Healey TJ, Tozer RC, Freeston IL (1992): Impedance imaging of 3D objects using magnetically induced currents. In Proc. 14th Annual Int. Conf. IEEE Eng. In Med. And Biol. Society, Paris, Vol. 14, ed. JP Morucci, R Plonsey, JL Coatrieux, S Laxminarayan, pp. 1719-20, IEEE, New York, N.Y.
Hua P, Webster JG, Tompkins WJ (1987): Effect of the measurement method on noise handling and image quality of EIT imaging. In Proc. Ninth Int. Conf. IEEE Eng. In Med. And Biol. Society, Vol. 2, pp. 1429-30, IEEE, New York, N.Y.
Kauppinen P, Hyttinen J, Malmivuo J (2006): Sensitivity distribution visualizations of impedance tomography measurement strategies. Int. J. Bioelectromagnetism 8:(1) pp. VII/1 - VII/9.
Purvis WR, Tozer RC, Freeston IL (1990): Impedance imaging using induced current. In Proc. 12th Annual Int. Conf. IEEE Eng. In Med. And Biol. Society, Vol. 1, pp. 114-5, IEEE, New York, N.Y.
Woo EJ (1990): Finite element method and reconstruction algorithms in electrical impedance tomography. Dept. of Electrical and Computer Eng., Univ. of Wisconsin, Madison, (Ph.D. thesis)
Woo EJ, Hua P, Webster JG, Tompkins WJ (1992): Measuring lung resistivity using electrical impedance tomography. IEEE Trans. Biomed. Eng. 39:(7) 756-60.
SÁCH THAM KHẢO
Brown BH, Barber DC (eds.) (1992): Electrical Impedance Tomography, 207 pp. The Institute of Physical Sciences in Medicine, York. (Clinical Physics and Physiological Measurement, Vol. 13, Suppl. A)
Hames TK (ed.) (1990): Proc. Meeting On Electrical Impedance Tomography, Copenhagen, 14th - 16th July 1990, 284 pp. European Community Concerted Action on Electrical Impedance Tomography, Brussels.
Krestel E (ed.) (1990): Imaging Systems for Medical Diagnostics, 636 pp. Siemens Aktiengesellschaft, Berlin and Munich.
Webb S (ed.) (1992): The Physics of Medical Imaging, 2nd ed., 633 pp. IOP Publishing Ltd, Bristol.
Webster JG (ed.) (1990): Electrical Impedance Tomography, 223 pp. Adam Hilger, Bristol and New York.
Wells PNT (ed.) (1982): Scientific Basis of Medical Imaging, 284 pp. Churchill Livingstone, New York.
| Trang trước | Cắt lớp trở kháng | Trang tiếp |


