Đại số 10/Chương I/§1. Mệnh đề
Mục lục
Lí thuyết[sửa]
Mệnh đề và các phép toán lôgic[sửa]
Mệnh đề[sửa]
| Hoạt động 1 |
Cho
các
câu
sau
đây:
a) Xét tính đúng/sai của các câu trên. b) Từ a) hãy xếp các câu trên thành hai loại. Các câu 1, 3, 6 và 8 là những câu có tính chất: hoặc đúng hoặc sai, không thể vừa đúng vừa sai. Các câu còn lại không đúng cũng không sai |
Trong toán học, ta hiểu một mệnh đề logic (gọi tắt là mệnh đề) là một phát biểu khẳng định một sự kiện nào đó, sao cho khẳng định đó nhận một trong hai giá trị "đúng" hoặc "sai".
Như vậy:
|
Mỗi
mệnh
đề
phải
đúng
hoặc
sai.
Một mệnh đề không thể vừa đúng, vừa sai. |
|
Kí hiệu:
-
Người
ta
thường
dùng
các
chữ
cái
a,
b,
c,...
A,
B,
C,...
để
kí
hiệu
cho
các
mệnh
đề.
Chẳng
hạn,
để
kí
hiệu
a/P
là
mệnh
đề
"Paris
là
thủ
đô
của
nước
Pháp"
ta
sẽ
viết:
- a = "Paris là thủ đô của nước Pháp" hoặc
- P : "Paris là thủ đô của nước Pháp".
| Hoạt động 2 |
Hãy
nêu
(nói/viết)
hai
câu,
một
câu
là
mệnh
đề
và
một
câu
không
là
mệnh
đề.
|
NHẬN
XÉT:
Nói chung những câu nghi vấn, câu cảm thán, câu mệnh lệnh đều không phải là mệnh đề.
Trong toán học, khi có hai số, người ta dùng các phép toán số học (cộng, trừ, nhân, chia,...) tác động vào chúng để nhận được những số mới. Tương tự, khi có mệnh đề, người ta dùng các phép lôgic tác động vào chúng để nhận được những mệnh đề mới. Dưới đây ta trình bày định nghĩa và một số tính chất cơ bản của các phép toán này.
Phủ định của một mệnh đề[sửa]
| VÍ DỤ 1 |
Xét
hai
mệnh
đề
Hai
mệnh
đề
A
và
|
Tổng
quát,
nếu
một
mệnh
đề
được
kí
hiệu
là
A,
thì
mệnh
đề
phủ
định
của
nó
được
kí
hiệu
là
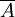 .
Do
ý
nghĩa
của
phủ
định,
ta
thấy:
.
Do
ý
nghĩa
của
phủ
định,
ta
thấy:
|
Nếu
mệnh
đề
A
là
đúng,
thì
mệnh
đề
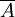 là
sai.
là
sai.
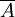 là
đúng.
là
đúng. |
|
| VÍ DỤ 2 |
Nếu
a
=
"Paris
là
thủ
đô
của
nước
Pháp"
thì
mệnh
đề
phủ
định
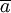 có
thể
diễn
đạt
như
sau:
có
thể
diễn
đạt
như
sau:
|
| VÍ DỤ 3 |
Nếu
b
=
"15
lớn
hơn
30"
thì
mệnh
đề
phủ
định
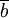 có
thể
diễn
đạt
như
sau:
có
thể
diễn
đạt
như
sau:
|
CHÚ
Ý:
Mệnh đề phủ định của a thường được diễn đạt là "không phải a".
Mệnh đề kéo theo[sửa]
Với hai mệnh đề a và b, một mệnh đề được thành lập từ hai mệnh đề a và b bởi cặp liên từ "Nếu... thì...":
được gọi là "mệnh đề kéo theo" của các mệnh đề a và b, kí hiệu là:
 b"
b"
| VÍ DỤ 4 |
Với
thì
"a
|
| VÍ DỤ 5 |
Với
thì
"a
|
Qua ví dụ 4 & 5, ta thấy:
|
Nếu
a
đúng
và
b
đúng
thì
"a
 b"
là
một
mệnh
đề
đúng.
b"
là
một
mệnh
đề
đúng.
Nếu
a
đúng
và
b
sai
thì
"a
|
|
| Hoạt động 4 |
Cho
các
mệnh
đề:
Hãy
xét
tính
đúng/sai
của
các
mệnh
đề:
a
|
NHẬN
XÉT:
-
Để
chứng
minh
mệnh
đề
a
 b
đúng
ta
chỉ
cần
xét
trường
hợp
a
và
b
cùng
đúng
và
phép
chứng
minh
mệnh
đề
a
b
đúng
ta
chỉ
cần
xét
trường
hợp
a
và
b
cùng
đúng
và
phép
chứng
minh
mệnh
đề
a
 b
được
tiến
hành
theo
ba
bước:
b
được
tiến
hành
theo
ba
bước:
- Bước 1. Giả sử a đúng.
- Bước 2. Từ giả thiết a đúng, dùng lập luận và các mệnh đề toán học đã biết, suy ra b đúng.
-
Bước
3.
Kết
luận
a
 b
luôn
đúng.
b
luôn
đúng.
CHÚ
Ý:
-
1.
Các
định
lí
toán
học
thường
là
những
mệnh
đề
đúng
và
có
dạng
"a
 b".
Trong
đó,
a
được
gọi
là
giả
thiết,
b
được
gọi
là
kết
luận
của
định
lí.
b".
Trong
đó,
a
được
gọi
là
giả
thiết,
b
được
gọi
là
kết
luận
của
định
lí. -
2.
Nếu
ta
coi
mệnh
đề
a
 b
là
mệnh
đề
thuận
thì
mệnh
đề:
b
là
mệnh
đề
thuận
thì
mệnh
đề:
-
-
b
 a
được
gọi
là
mệnh
đề
đảo
a
được
gọi
là
mệnh
đề
đảo -
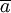

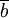 là
mệnh
đề
phản
là
mệnh
đề
phản -
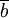

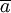 là
mệnh
đề
phản
đảo.
là
mệnh
đề
phản
đảo.
-
b
-
- 3. Mệnh đề "Nếu a thì b" thường được diễn đạt dưới nhiều hình thức khác nhau, chẳng hạn:
"Có b khi có a"
"Từ a suy ra b"
"a là điều kiện đủ để có b"
"b là điều kiện cần (ắt có) để có a"
..............
-
-
Ví
dụ:
-
- "15 có chữ số tận cùng bằng 5 suy ra 15 chia hết cho 5" ← mệnh đề đúng.
- "Nếu dây tóc bóng đèn có dòng điện chạy qua thì bóng đèn sáng" ← mệnh đề đúng.
-
-
Ví
dụ:
- 4. Trong văn học, mệnh đề kéo theo còn được diễn đạt bằng nhiều hình thức phong phú. Chẳng hạn:
Bấy giờ dì ghẻ mới thương con chồng"
- hoặc
Bay cao thì nắng bay vừa thì dâm".
Mệnh đề Đảo. Hai mệnh đề tương đương[sửa]
| Hoạt động 5 |
Cho
tam
giác
ABC.
Xét
các
mệnh
đề
dạng
"a
 b"
sau:
b"
sau:
a) Nếu tam giác ABC là một tam giác đều thì ABC là một tam giác cân. b) Nếu tam giác ABC là một tam giác đều thì ABC là một tam giác cân và có một góc bằng 60°.
Hãy
phát
biểu
các
mệnh
đề
"b
|
Như
trên,
ta
đã
biết,
các
mệnh
đề
dạng
"b
 a"
được
gọi
là
mệnh
đề
đảo
của
mệnh
đề
"a
a"
được
gọi
là
mệnh
đề
đảo
của
mệnh
đề
"a
 b".
b".
Dễ thấy rằng, mệnh đề đảo của một mệnh đề không nhất thiết là đúng. Chẳng hạn:
nhưng mệnh đề đảo của nó:
Trường hợp đặc biệt:
|
Khi
cả
hai
mệnh
đề
"a
 b"
và
"b
b"
và
"b
 a"
cùng
đúng(*)
ta
nói
a
và
b
là
hai
mệnh
đề
tương
đương.
Kí
hiệu
là:
a"
cùng
đúng(*)
ta
nói
a
và
b
là
hai
mệnh
đề
tương
đương.
Kí
hiệu
là:
 b
bđọc là
|
|
| VÍ DỤ 6 |
Tam
giác
ABC
cân
và
có
một
góc
60°
là
điều
kiện
cần
và
đủ
để
tam
giác
ABC
đều.
Một tam giác là tam giác vuông khi và chỉ khi nó có một góc bằng tổng hai góc còn lại. |
CHÚ
Ý:
-
1.
Tổng
quát,
(*)
hai
mệnh
đề
a,
b
tương
đương
với
nhau
hoàn
toàn
không
có
nghĩa
là
nội
dung
của
chúng
như
nhau,
mà
nó
chỉ
nói
lên
rằng
chúng
có
cùng
giá
trị
chân
lí
(cùng
đúng
hoặc
cùng
sai).
-
-
Ví
dụ:
- "Tháng 12 có 31 ngày khi và chỉ khi trái đất quay quanh mặt trời" là mệnh đề đúng.
- "12 giờ trưa hôm nay Tuấn có mặt ở Hà Nội nếu và chỉ nếu vào giờ đó anh đang ở thành phố Hồ Chí Minh" là mệnh đề sai.
- "Hình vuông có một góc tù khi và chỉ khi 100 là số nguyên tố" là mệnh đề đúng.
-
Ví
dụ:
-
-
3.
Để
chứng
minh
mệnh
đề
a
 b
ta
chứng
minh
hai
mệnh
đề
a
b
ta
chứng
minh
hai
mệnh
đề
a
 b
và
b
b
và
b
 a.
a. - 4. Các cặp mệnh đề thuận và phản đảo, đảo và phản là những cặp mệnh đề tương đương.
Hàm mệnh đề. Các lượng từ tồn tại và tổng quát[sửa]
Hàm mệnh đề[sửa]
Ta xét các ví dụ sau:
Ví dụ 1: "Số tự nhiên n chia hết cho 5".
Về phương diện ngôn ngữ thì đây là một câu. Nhưng câu này chưa phản ánh tính đúng hoặc sai một thực tế khách quan nào, cho nên nó chưa phải là mệnh đề. Song nếu ta thay n bằng số tự nhiên cụ thể, chẳng hạn:
-
- Thay n = 100 ta được mệnh đề đúng: "Số 100 chia hết cho 5".
- Thay n = 101 ta được mệnh đề sai: "Số 101 chia hết cho 5".
Ví dụ 2: "x + 3 > 7".
Tương tự như trong ví dụ 1, x + 3 > 7 chưa phải là mệnh đề, song nếu ta thay x bởi một số thực cụ thể, chẳng hạn:
-
- Thay x = 0 ta được mệnh đề sai: "0 + 3 > 7".
- Thay x = 5 ta được mệnh đề đúng: "5 + 3 > 7".
Ví dụ 3: "Ông A là nhà toán học vĩ đại".
Câu trên chưa phải là mệnh đề. Nhưng nếu ta chọn "ông A" là "Gausơ" sẽ được mệnh đề đúng: "Gausơ là nhà toán học vĩ đại", nếu ta chọn "ông A" là "Đinh Bộ Lĩnh" thì sẽ được mệnh đề sai: "Đinh Bộ Lĩnh là nhà toán học vĩ đại".
Từ các ví dụ trên ta đi đến định nghĩa sau:
|
Những
câu
có
chứa
các
biến
mà
bản
thân
nó
chưa
phải
là
mệnh
đề
nhưng
khi
ta
thay
các
biến
đó
bởi
các
phần
tử
thuộc
tập
xác
định
X
thì
nó
trở
thành
mệnh
đề
(đúng
hoặc
sai)
ta
sẽ
gọi
là
hàm
mệnh
đề
(hoặc
vị
từ,
hàm
phán
đoán,
mệnh
đề
không
xác
định,
mệnh
đề
chứa
biến).
Tập
X
gọi
là
miền
xác
định
của
hàm
mệnh
đề
đó.
|
|
Ta
dùng
kí
hiệu:
T(n),
F(x),...
để
chỉ
các
hàm
mệnh
đề.
Chẳng hạn:
-
- Hàm mệnh đề T(n): "Số tự nhiên n chia hết cho 5" có miền xác định là tập các số tự nhiên N. Tập các số tự nhiên có tận cùng bằng 0 hoặc 5 là miền đúng của T(n).
- Hàm mệnh đề F(x) = "x + 3 > 7" có miền xác định là các số thực. Tập các số thực lớn hơn 4 ta gọi là miền đúng của hàm mệnh đề F(x).
Mệnh đề tồn tại[sửa]
|
Cho
T(x)
là
hàm
mệnh
đề
xác
định
trên
miền
X.
Nếu
ta
đặt
thêm
cụm
từ
"Tồn
tại
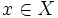 sao
cho
..."
vào
trước
hàm
mệnh
đề
T(x)
ta
được
mệnh
đề:
sao
cho
..."
vào
trước
hàm
mệnh
đề
T(x)
ta
được
mệnh
đề:
Ta gọi mệnh đề có cấu trúc như trên là mệnh đề tồn tại. Kí hiệu là: 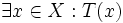 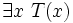 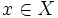
|
|
Kí
hiệu
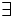 gọi
là
lượng
từ
tồn
tại.
gọi
là
lượng
từ
tồn
tại.
Ví dụ:
-
- "Tồn tại số thực x sao cho x + 3 > 7" là mệnh đề đúng.
-
Kí
hiệu
là:
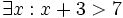
- "Tồn tại số tự nhiên n sao cho n chia hết cho 5" là mệnh đề đúng.
-
Kí
hiệu
là:
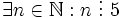
- "Tồn tại số thực x sao cho x2 + 1 = 0" là mệnh đề sai.
-
Kí
hiệu
là:
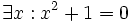
CHÚ
Ý:
-
1.
Trong
thực
tế,
mệnh
đề
tồn
tại
còn
được
diễn
đạt
dưới
những
dạng
khác
nhau,
chẳng
hạn:
-
-
"Tồn
tại
ít
nhất
một
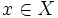 sao
cho
T(x)".
sao
cho
T(x)". -
"Có
một
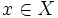 sao
cho
T(x)".
sao
cho
T(x)". -
"Có
ít
nhất
một
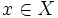 sao
cho
T(x)".
sao
cho
T(x)". - "Ít ra cũng có một người là nhà toán học".
- "Một số người là nhà toán học".
- "Có nhiều người là nhà toán học"
- ..................
-
"Tồn
tại
ít
nhất
một
-
-
2.
Ta
dùng
kí
hiệu
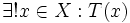 với
nghĩa
"Tồn
tại
duy
nhất
một
với
nghĩa
"Tồn
tại
duy
nhất
một
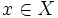 sao
cho
T(x)".
sao
cho
T(x)".
| Hoạt động 5 |
Phát
biểu
thành
lời
mệnh
đề
sau:
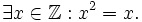 Mệnh đề này đúng hay sai? |
Mệnh đề tổng quát[sửa]
|
Cho
T(x)
là
hàm
mệnh
đề
xác
định
trên
miền
X.
Nếu
ta
đặt
thêm
cụm
từ
"Với
mọi
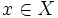 ta
có
..."
vào
trước
hàm
mệnh
đề
T(x)
ta
được
mệnh
đề:
ta
có
..."
vào
trước
hàm
mệnh
đề
T(x)
ta
được
mệnh
đề:
Ta gọi mệnh đề có cấu trúc như trên là mệnh đề tổng quát (hoặc toàn thể, phổ biến, phổ cập,...). Kí hiệu là: 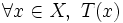 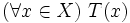 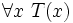 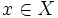
|
|
Kí
hiệu
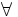 gọi
là
lượng
từ
tổng
quát
(hay
toàn
thể,
phổ
biến,
phổ
cập,...)
gọi
là
lượng
từ
tổng
quát
(hay
toàn
thể,
phổ
biến,
phổ
cập,...)
Ví dụ:
-
- "Với mọi số tự nhiên n ta có n chia hết cho 5" là mệnh đề sai.
-
Kí
hiệu
là:
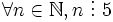
- "Với mọi số thực x ta có x + 3 > 7" là mệnh đề sai.
-
Kí
hiệu
là:
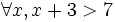
- "Với mọi số thực x ta có x2 + 1 > 0" là mệnh đề đúng.
-
Kí
hiệu
là:
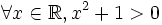
CHÚ
Ý:
Trong
thực
tế,
mệnh
đề
tổng
quát
thường
được
diễn
đạt
dưới
nhiều
hình
thức
khác
nhau,
chẳng
hạn:
-
-
- "Tất cả người Việt Nam đều nói tiếng Anh".
- "Mọi người Việt Nam đều nói thạo tiếng Anh".
- "Người Việt Nam nào cũng nói thạo tiếng Anh".
- "Đã là người Việt Nam thì ai chẳng nói thạo tiếng Anh".
- ....................
-
| Hoạt động 6 |
Phát
biểu
thành
lời
mệnh
đề
sau:
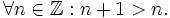 Mệnh đề này đúng hay sai? |
Phủ định của mệnh đề tồn tại và tổng quát[sửa]
Xét ví dụ sau:
| VÍ DỤ 7 |
Cho
hai
mệnh
đề:
a
=
"Mọi
số
thực
đều
có
bình
phương
khác
1"
và
b
=
"Có
một
số
tự
nhiên
n
mà
2n
=
1".
a) Phát biểu mệnh đề phủ định của các mệnh đề trên.
b)
Dùng
các
lượng
từ
tổng
quát
và
tồn
tại
để
viết
lại
các
mệnh
đề
a,
|
| Lời giải |
a)
Phủ
định
của
mệnh
đề
là
Phủ định của mệnh đề
là
b) Ta có
|
Tổng
quát,
ta
có
hai
mệnh
đề:
-
-
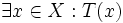 và
và
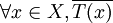 là
phủ
định
của
nhau.
là
phủ
định
của
nhau. -
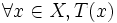 và
và
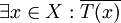 là
phủ
định
của
nhau.
là
phủ
định
của
nhau.
-
| Hoạt động 7 |
Hãy
phát
biểu
mệnh
đề
phủ
định
của
các
mệnh
đề
sau:
Dùng các lượng từ tổng quát và tồn tại để viết lại các mệnh đề a, b và các mệnh đề phủ định của chúng. |
BÀI TẬP[sửa]
-
Trong
các
câu
sau,
câu
nào
là
mệnh
đề,
câu
nào
là
mệnh
đề
chứa
biến?
- a) 3 + 2 = 7; b) 4 + x = 3;
- c) x + y > 1; d) 2 - √5 < 0.
-
Xét
tính
đúng
sai
của
mỗi
mệnh
đề
sau
và
phát
biểu
mệnh
đề
phủ
định
của
nó.
- a) 1794 chia hết cho 3; b) √2 là một số hữu tỉ;
- c) π < 3,15; d) |-125| ≤ 0.
-
Cho
các
mệnh
đề
kéo
theo:
-
- Nếu a và b cùng chia hết cho c thì a + b chia hết cho c (a, b, c là những số nguyên).
- Các số nguyên có tận cùng bằng 0 đều chia hết cho 5.
- Tam giác cân có hai trung tuyến bằng nhau.
- Hai tam giác bằng nhau có diện tích bằng nhau.
- a) Hãy phát biểu mệnh đề đảo của mỗi mệnh đề trên.
- b) Phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái niệm "điều kiện đủ".
- c) Phát biểu mỗi mệnh đề trên, bằng cách sử dụng khái niệm "điều kiện cần".
-
-
Phát
biểu
mỗi
mệnh
đề
sau,
bằng
cách
sử
dụng
khái
niệm
"điều
kiện
cần
và
đủ".
- a) Một số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và ngược lại.
- b) Một hình bình hành có các đường chéo vuông góc là một hình thoi và ngược lại.
- c) Phương trình bậc hai có hai nghiệm phân biệt khi và chỉ khi biệt thức của nó dương.
-
Dùng
kí
hiệu
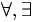 để
viết
các
mệnh
đề
sau:
để
viết
các
mệnh
đề
sau:
- a) Mọi số nhân với 1 đều bằng chính nó.
- b) Có một số cộng với chính nó bằng 0.
- c) Mọi số cộng với số đối của nó đều bằng 0.
-
Phát
biểu
thành
lời
mỗi
mệnh
đề
sau
và
xét
tính
đúng
sai
của
nó:
-
a)
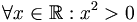 ;
b)
;
b)
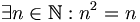 ;
; -
c)
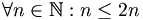 ;
d)
;
d)
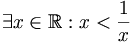 .
.
-
a)
-
Lập
mệnh
đề
phủ
định
của
mỗi
mệnh
đề
sau
và
xét
tính
đúng
sai
của
nó:
-
a)
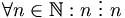 ;
b)
;
b)
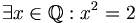 ;
; -
-
b)
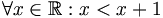 ;
d)
;
d)
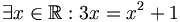 .
.
-
a)



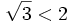 "
và
d
=
"3
<
4".
"
và
d
=
"3
<
4".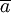 ,
b
và
,
b
và
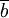 .
.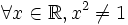 "
và
"
và
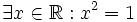 "
"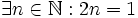 "
và
"
và
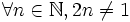 "
"

