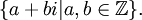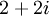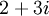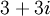Số nguyên Gauss
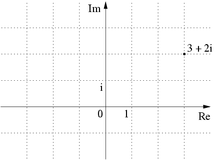
Một số nguyên Gauss là một số phức với phần thực và phần ảo đều là các số nguyên. Tập các số nguyên Gauss là một miền nguyên, thường được ký hiệu là Z[i].
Như vậy, các số nguyên Gauss là tập hợp
Chuẩn của số nguyên Gauss là số tự nhiên xác định bằng
- N(a + bi) = a2 + b2.
Chuẩn có tính chất nhân, nghiã là
- N(z·w) = N(z)·N(w).
Đơn vị của Z[i] là tất cả các phần tử có chuẩn bằng 1, nghĩa là gồm các phần tử
- 1, −1, i và −i.
Nếu g là số Gauss, thì các số sau được gọi là số liên kết (tiếng Anh là associate)với nó:
- g, -g, ig, -ig.
Số nguyên tố Gauss[sửa]
Các phần tử nguyên tố của Z[i] cũng được gọi là các số nguyên tố Gauss. Số nguyên tố Gauss không thể có ước nào khác ngoài các đơn vị của Z[i] và các liên kết của nó. Nói một cách khác, số nguyên Gauss g nguyên tố khi và chỉ khi g không thể phân tích thành tích của các số nguyên Gauss p và q với chuẩn |p|>1 và |q|>1.
Một số nguyên Gauss a+bi được gọi là số nguyên tố nếu và chỉ nếu nó thỏa mãn một trong các tiêu chuẩn sau:
- a=0 và |b| là số nguyên tố có dạng 4k+3;
- b=0 và |a| là số nguyên tố có dạng 4k+3;
-
a
và
b
đều
khác
0
và
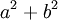 là
một
số
nguyên
tố.
là
một
số
nguyên
tố.
Một vài số nguyên tố thông thường (đôi khi để phân biệt, chúng được gọi là các "số nguyên tố hữu tỷ") không phải là các số nguyên tố Gauss; chẳng hạn 2 = (1 + i)(1 − i) và 5 = (2 + i)(2 − i). Các số nguyên tố hữu tỷ đồng dư với 3 (mod 4) là số nguyên tố Gauss; còn các số nguyên tố hữu tỷ đồng dư 1 (mod 4) thì không. Đó là vì số nguyên tố dạng 4k + 1 luôn có thể viết dưới dạng tổng của hai bình phương (định lý Fermat về tổng của hai số chính phương), do đó ta có
- p = a2 + b2 = (a + bi)(a − bi).
Nếu chuẩn của số nguyên Gauss z là một số nguyên tố, thì z cũng là số nguyên tố Gauss, vì mọi ước không tầm thường của z cũng là ước không tầm thường của chuẩn. Chẳng hạn 2 + 3i là một số nguyên tố Gauss vì chuẩn của nó là 4 + 9 = 13.
Phép chia Euclid[sửa]
Tính chất của chuẩn cho phép ta xác định phép chia Euclid với các số nguyên Gauss:
- Cho 2 số nguyên Gauss a và b, khi đó tồn tại các số nguyên q và r sao cho:
-
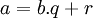 với
N(r)<N(b).
với
N(r)<N(b).
Ví dụ:
-
Cho
các
số
nguyên
Gauss:
-
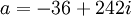
-
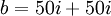
-
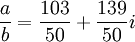 ,
,
-
-
ta
cần
xác
định
số
nguyên
Gauss
q
gần
với
thương
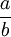 nhất.
nhất. -
Trong
hình
vẽ
bên,
trên
mặt
phẳng
số
phức,
thương
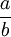 được
biểu
thị
bằng
một
chấm
đen,
nằm
trong
ô
vuông
độ
dài
đơn
vị
với
4
đỉnh
là
4
số
nguyên
Gauss,
ô
vuông
này
được
tô
màu
đỏ
nâu
nhạt.
Do
khoảng
cách
giữa
điểm
được
biểu
thị
bằng
một
chấm
đen,
nằm
trong
ô
vuông
độ
dài
đơn
vị
với
4
đỉnh
là
4
số
nguyên
Gauss,
ô
vuông
này
được
tô
màu
đỏ
nâu
nhạt.
Do
khoảng
cách
giữa
điểm
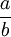 và
q
không
quá
1,
giá
trị
của
q
chỉ
có
thể
là
số
nguyên
Gauss
biểu
thị
bởi
4
đỉnh
này.
và
q
không
quá
1,
giá
trị
của
q
chỉ
có
thể
là
số
nguyên
Gauss
biểu
thị
bởi
4
đỉnh
này. -
Ta
vẽ
4
đường
tròn
bán
kính
đơn
vị
nhận
4
đỉnh
trên
làm
tâm
(các
đường
tròn
này
tô
màu
xanh
nhạt).
Nếu
điểm
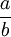 nằm
trong
đường
tròn
nào
thì
q
có
thể
nhận
giá
trị
tại
tâm
đường
tròn
đó.
nằm
trong
đường
tròn
nào
thì
q
có
thể
nhận
giá
trị
tại
tâm
đường
tròn
đó. -
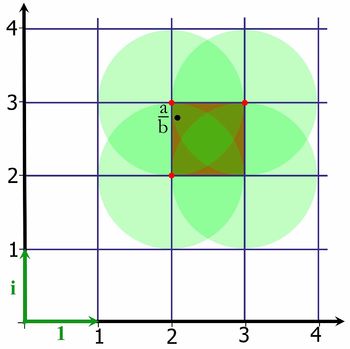
Nhìn
vào
hình
vẽ
ta
thấy
q
chỉ
nằm
trong
3
đường
tròn
có
tâm
là
điểm
tô
màu
đỏ,
và
do
đó
có
thể
nhận
một
trong
các
giá
trị
bằng:
-
Phép chia Euclid[sửa]
Tính chất của chuẩn cho phép ta xác định phép chia Euclid với các số nguyên Gauss:
- Cho 2 số nguyên Gauss a và b, khi đó tồn tại các số nguyên q và r sao cho:
-
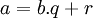 với
N(r)<N(b).
với
N(r)<N(b).
Ví dụ:
-
Cho
các
số
nguyên
Gauss:
-
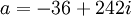
-
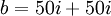
-
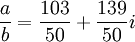 ,
,
-
-
ta
cần
xác
định
số
nguyên
Gauss
q
gần
với
thương
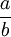 nhất.
nhất. -
Trong
hình
vẽ
bên,
trên
mặt
phẳng
số
phức,
thương
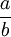 được
biểu
thị
bằng
một
chấm
đen,
nằm
trong
ô
vuông
độ
dài
đơn
vị
với
4
đỉnh
là
4
số
nguyên
Gauss,
ô
vuông
này
được
tô
màu
đỏ
nâu
nhạt.
Do
khoảng
cách
giữa
điểm
được
biểu
thị
bằng
một
chấm
đen,
nằm
trong
ô
vuông
độ
dài
đơn
vị
với
4
đỉnh
là
4
số
nguyên
Gauss,
ô
vuông
này
được
tô
màu
đỏ
nâu
nhạt.
Do
khoảng
cách
giữa
điểm
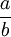 và
q
không
quá
1,
giá
trị
của
q
chỉ
có
thể
là
số
nguyên
Gauss
biểu
thị
bởi
4
đỉnh
này.
và
q
không
quá
1,
giá
trị
của
q
chỉ
có
thể
là
số
nguyên
Gauss
biểu
thị
bởi
4
đỉnh
này. -
Ta
vẽ
4
đường
tròn
bán
kính
đơn
vị
nhận
4
đỉnh
trên
làm
tâm
(các
đường
tròn
này
tô
màu
xanh
nhạt).
Nếu
điểm
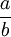 nằm
trong
đường
tròn
nào
thì
q
có
thể
nhận
giá
trị
tại
tâm
đường
tròn
đó.
nằm
trong
đường
tròn
nào
thì
q
có
thể
nhận
giá
trị
tại
tâm
đường
tròn
đó. -
Nhìn
vào
hình
vẽ
ta
thấy
q
chỉ
nằm
trong
3
đường
tròn
có
tâm
là
điểm
tô
màu
đỏ,
và
do
đó
có
thể
nhận
một
trong
các
giá
trị
bằng:
-