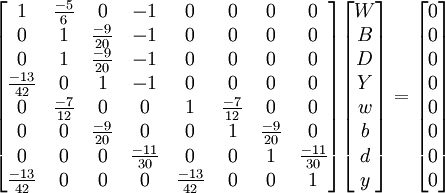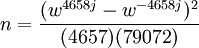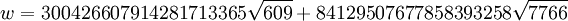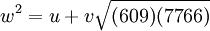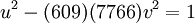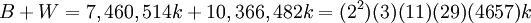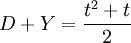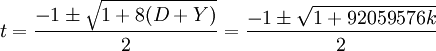Đàn gia súc của Archimedes
Bài toán đàn gia súc Ác-si-mét (tiếng Anh: Archimedes' cattle problem) là một bài toán giải phương trình Đi-ô-phăng. Bài toán yêu cầu tính số bò trong đàn gia súc của Thần Mặt Trời. Bài toán được Gothold Ephraim Lessing phát hiện ra trong một văn bản Hy Lạp cổ, dưới dạng một bài thơ 44 dòng. Văn bản đó được tìm thấy ở trong thư viện Herzog August ở Wolfenbüttel, Đức năm 1773.
Việc giải bài toán dẫn đến giải một phương trình Pell có vô số nghiệm. Chính vì thế, người ta chỉ quan tâm đến nghiệm nguyên dương nhỏ nhất (các nghiệm còn lại đều biểu diễn bằng công thức tổng quát qua nghiệm nhỏ nhất này). Nhưng ngay cả nghiệm nhỏ nhất này cũng quá lớn (tới 206545 chữ số). Vì lý do đó mà trong nhiều năm, bài toán không có lời giải cuối cùng. Đến năm 1880, A. Amthor đã tìm ra lời giải tổng quát, với đáp số chính xác đến lũy thừa. Kết quả chính xác không thể tính ra chỉ bằng bút chì và giấy, vì số lượng chữ số quá lớn. Tuy vậy, ngày nay, các phần mềm máy tính cho phép viết kết quả chính xác này ra.
Lịch sử[sửa]
Vào năm 1769, Gotthold Ephraim Lessing được bổ nhiệm làm thủ thư tại thư viện Herzog August ở Wolfenbüttel, nơi lưu trữ nhiều văn bản tiếng Hy Lạp và Latin.[1] Vài năm sau, Lessing cho xuất bản một số bản dịch kèm theo lời bình. Trong số đó có một bài thơ Hy Lạp dài 44 dòng, thách đố người đọc tìm ra số gia súc trong đàn gia súc của Thần Mặt Trời. Phần đầu bài thơ nói rằng, Ác-si-mét đã gửi nó cho Eratosthenes để các nhà toán học ở Alexandria nghiên cứu. Vấn đề liệu Ác-si-mét có phải là tác giả của bài thơ hay không còn đang được tranh luận, mặc dù người ta không tìm thấy chút manh mối nào của bài thơ này trong bài viết của các nhà toán học Hy Lạp khác. [2]
Lời giải tổng quát được A. Amthor [3] tìm ra đầu tiên, vào năm 1880. Kết quả được ước tính có 206 545 chữ số với 3 chữ số đầu tiên là 776.
Những tính toán của Amthor được tiếp tục bởi nhóm Câu lạc bộ Toán học Hillsboro (Hillsboro, Illinois, Hoa Kỳ) từ năm 1889 đến 1893. Ba thành viên của câu lạc bộ gồm Edmund Fish, Geo. H. Richards, và A. H. Bell đã tính 31 chữ số đầu tiên và 12 chữ số cuối cùng của đáp số nhỏ nhất của bài toán:
7760271406486818269530232833209 . . . 719455081800
Trong kết quả này, hai chữ số in đậm bị tính sai, kết quả đúng phải là 13. Kết quả được công bố trên bài báo
A. H. Bell "The "Cattle Problem." ByArchimedies[sic] 251 TCN" American Mathematical Monthly Volume 2 (1895) pages 140-141
Thời
đại
máy
tính
cho
phép
giải
quyết
bài
toán
trọn
vẹn.
Nghĩa
là
kết
quả
được
tính
chính
xác
đến
từng
chữ
số.
Điều
đó
được
thực
hiện
lần
đầu
tiên
ở
đại
học
Waterloo,
vào
năm
1965
bởi
H.
C.
Williams,
R.
A.
German,
và
C.
R.
Zarnke.
Họ
dùng
2
máy
tính
IBM
7040
và
IBM
1620.
H.
C.
Williams,
R.
A.
German,
and
C.
R.
Zarnke
"Solution
of
the
cattle
problem
of
Archimedes"
Mathematics
of
Computation
Volume
XIX
(1965)
pages
671-674
Năm
1981,
Harry
L.
Nelson
của
Phòng
thí
nghiệm
quốc
gia
Lawrence
Livermore
(Lawrence
Livermore
National
Laboratory)
đã
in
kết
quả
gồm
206545
chữ
số,
tính
bởi
máy
tính
CRAY
1
(số
lượng
gia
súc
nhỏ
nhất
có
thể
của
Thần
Mặt
Trời).
Harry
L.
Nelson
"A
solution
to
Archimedes'
cattle
problem"
Journal
of
Recreational
Mathematics
Volume
13
(1980-81)
pages
162-176
Bài toán[sửa]
Sau đây là bản dịch tiếng Việt từ bản rút gọn tiếng Anh từ bản dịch tiếng Anh từ bản dịch tiếng Đức từ bản gốc tiếng Hy Lạp, được xuất bản vào năm 1842 bởi Nesselmann, và vào năm 1880 bởi Krumbiegel:
Bản dịch thơ
Này bạn, hãy nhìn
Đàn gia súc của Thần Mặt Trời
Thảnh thơi gặm cỏ trên cánh đồng đảo Sicily.
Bốn đàn nhỏ theo màu,
Trắng sữa, đen, đốm và vàng.
Số bò đực nhiều hơn số bò cái.
Nếu biết:
-
Bò
đực
trắng
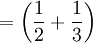 bò
đực
đen
+
bò
đực
vàng,
bò
đực
đen
+
bò
đực
vàng, -
Bò
đực
đen
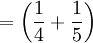 bò
đực
đốm
+
bò
đực
vàng,
bò
đực
đốm
+
bò
đực
vàng, -
Bò
đực
đốm
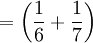 bò
đực
trắng
+
bò
đực
vàng,
bò
đực
trắng
+
bò
đực
vàng, -
Bò
cái
trắng
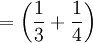 bò
đen,
bò
đen, -
Bò
cái
đen
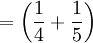 bò
đốm,
bò
đốm, -
Bò
cái
đốm
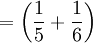 bò
vàng,
bò
vàng, -
Bò
cái
vàng
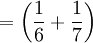 bò
trắng.
bò
trắng.
Có thể biết bao nhiêu
Bò đực,
Bò cái??
Trả lời đi, người bạn của tôi
Ồ! bạn nói không,
Ôi đứa trẻ trong trò chơi với những con số.
Nếu biết thêm:
- Bò đực trắng + Bò đực đen = số chính phương,
- Bò đực đốm + bò đực vàng = số tam giác.
Hãy nói đi,
Số bò cả thảy,
Và bạn thành người chiến thắng.
Vỗ ngực tự hào,
Những con số
Giờ đây khuất đầu chịu thua.
Bản dịch dưới dạng văn xuôi
- Trên đồng cỏ ở đảo Sicily, đàn bò của thần Mặt Trời đang gặm cỏ. Tính số bò đực và bò cái trong đàn nếu biết:
- 1/ đàn gồm có bốn màu: trắng sữa, đen, đốm và vàng;
- 2/ số bò đực nhiều hơn số bò cái;
- 3/
-
bò
đực
trắng
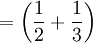 bò
đực
đen
+
bò
đực
vàng,
bò
đực
đen
+
bò
đực
vàng, -
bò
đực
đen
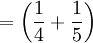 bò
đực
đốm
+
bò
đực
vàng,
bò
đực
đốm
+
bò
đực
vàng, -
bò
đực
đốm
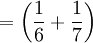 bò
đực
trắng
+
bò
đực
vàng,
bò
đực
trắng
+
bò
đực
vàng, -
bò
cái
trắng
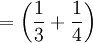 bò
đen,
bò
đen, -
bò
cái
đen
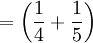 bò
đốm,
bò
đốm, -
bò
cái
đốm
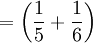 bò
vàng,
bò
vàng, -
bò
cái
vàng
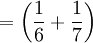 bò
trắng.
bò
trắng. - 4/
- bò đực trắng + Bò đực đen = số chính phương,
- bò đực đốm + bò đực vàng = số tam giác.
Lời giải[sửa]
Sử
dụng
phương
pháp
đại
số,
giải
hệ
phương
trình
tuyến
tính.
Kí
hiệu
số
bò
đực
màu
trắng,
đen,
đốm
và
vàng
là
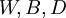 và
và
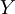 .
Số
bò
cái
màu
trắng,
đen,
đốm
và
vàng
là
.
Số
bò
cái
màu
trắng,
đen,
đốm
và
vàng
là
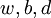 và
và
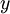 .
.
Mối liên hệ giữa số lượng bò mỗi màu chuyển về hệ phương trình:
-
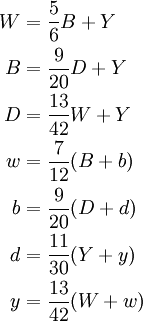 .
.
Hệ phương trình này có 8 ẩn và 7 phương trình. Do đó hệ vô số nghiệm.
Biểu diễn hệ theo ma trận, với thứ tự các biến là W, B, D, Y, w, b, d, y: thì:
Có
thể
giải
theo
cách
phổ
thông.
Ta
biểu
diễn
các
nghiệm
theo
công
thức
tổng
quát:
-
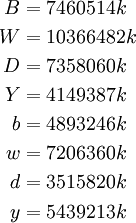 .
.
Như số lượng bò gấp 50 389 082 lần k.
4 số đầu tiên đều chia hết cho 4657. Con số này ta sẽ gặp nhiều về sau.
Lời giải tổng quát được A. Amthor [3] tìm ra vào năm 1880. Lời diễn giải sau đây là của H. W. Lenstra [4], dựa trên phương trình Pell.
Nhân các nghiệm tổng quát vừa tìm được với:
trong đó
và j là số nguyên dương bất kì. w có thể biểu diễn tương đương
với {u, v} là nghiệm cơ bản của phương trình Pell
Muốn số lượng gia súc là nhỏ nhất thì chọn j nhỏ nhất, j = 1.
Đáp
số:
số
lượng
gia
súc
của
Thần
Mặt
Trời
xấp
xỉ
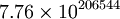 (kết
quả
này
được
A.
Amthor
công
bố
đầu
tiên).
(kết
quả
này
được
A.
Amthor
công
bố
đầu
tiên).
Ngày nay, các máy tính có thể dễ dàng tính ra kết quả chính xác đến từng chữ số của bài toán này. Điều đó được thực hiện lần đầu tiên ở đại học Waterloo, vào năm 1965 bởi H. C. Williams, R. A. German, và C. R. Zarnke. Họ dùng kết hợp máy tính IBM 7040 và IBM 1620.
Phương trình Pell[sửa]
Với dữ kiện thứ hai của bài toán.
Tổng số bò đực đen và bò đực trắng là số chính phương:
suy ra k = (3)(11)(29)(4657)q2, với q là số nguyên.
Tổng số bò đực đốm và bò đực vàng là số tam giác:
suy ra:
Suy ra 1+92059576k là số chính phương, dẫn đến phương trình Pell sau (thay k = (3)(11)(29)(4657)q2 )
-
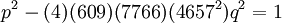 .
.
Tham khảo[sửa]
Lỗi
chú
thích:
Tồn
tại
thẻ
<ref>,
nhưng
không
tìm
thấy
thẻ
<references/>