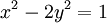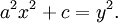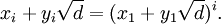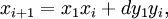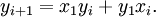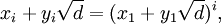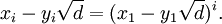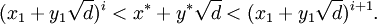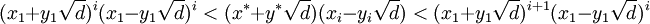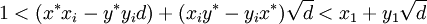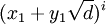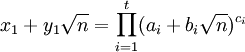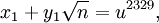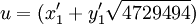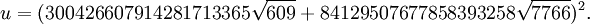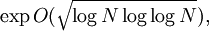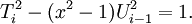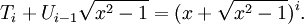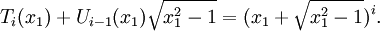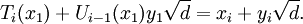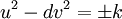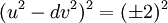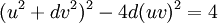Phương trình Pell
Phương trình Pell (Pell's equation) là bài toán tìm nghiệm nguyên Diophantine bậc hai. Yêu cầu đặt ra là giải phương trình nghiệm nguyên sau:
- dạng chính tắc:
-
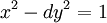 .
.
- dạng phương trình Pell âm:
-
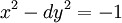 .
.
- Với d là số nguyên dương và không phải là số chính phương.
Lagrange chứng minh rằng với d không phải là số chính phương, phương trình Pell có vô số nghiệm nguyên dương.
Phương trình được đặt tên là Pell, do sơ suất của Leonhard Euler. Khi Euler đọc tác phẩm của Lord Brouncker, nhà toán học châu Âu đầu tiên tìm ra lời giải tổng quát của bài toán, Euler đã nhầm Brouncker với John Pell.
Phương trình này được nghiên cứu đầu tiên ở Ấn Độ cổ đại, bởi Brahmagupta (Brahmagupta là người đã phát triển phương pháp chakravala nhằm giải quyết phương trình Pell và các phương trình bậc hai bất định khác trong tác phẩm Brahma Sphuta Siddhanta vào năm 628, trước Pell 1000 năm). Tác phẩm Brahma Sphuta Siddhanta đã được dịch sang tiếng Arap vào năm 773, và dịch sang tiếng Latin vào năm 1126. Braskara II vào thế kỉ 12 và Narayana vào thế kỉ 14 đã tìm ra lời giải tổng quát cho phương trình Pell và các phương trình bậc hai bất định khác.
Lời giải cho một số dạng đặc biệt của phương trình Pell (ví dụ khi số biến nhiều hơn 2), được biến đến từ rất lâu từ thời Pi-ta-go ở Hy Lạp cổ.
Muốn biết rõ hơn, hãy xem Lenstra (2002) and Barbeau (2003).
Mục lục
Lịch sử[sửa]
Từ năm 400 TCN, ở Ấn Độ và Hy Lạp, người ta đã nghiên cứu phương trình Pell. Chủ yếu trong trường hợp riêng :
vì
có
nghiệm
liên
quan
đến
căn
bậc
hai
của
2.
Cụ
thể
hơn,
nếu
x
,
y
là
nghiệm
nguyên
của
phương
trình
này,
thì
x / y
xấp
xỉ
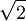 .
Braudhayana
khám
phá
ra
rằng,
với
x
=
17,
y
=
12
and
x
=
577,
y
=
408
là
2
nghiệm
của
phương
trình
Pell,
đồng
thời
17 / 12,
577 / 408
xấp
xỉ
rất
sát
với
.
Braudhayana
khám
phá
ra
rằng,
với
x
=
17,
y
=
12
and
x
=
577,
y
=
408
là
2
nghiệm
của
phương
trình
Pell,
đồng
thời
17 / 12,
577 / 408
xấp
xỉ
rất
sát
với
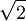 .
.
Sau đó, Ácsimét đã sử dụng một phương trình tương tự để ước lượng căn bậc hai của 3, và tìm ra phân số 1351/780.
Vào khoảng năm 250 Công Nguyên, Diophantus (Diophantine) đã nghiên cứu 1 dạng khác của phương trình Pell:
Diophantus đã giải phương trình trong trường hợp a = 1 và c = −1, 1, và 12, và cho a = 3 and c = 9.
Brahmagupta phát minh ra phương pháp tổng quát cho phương trình Pell, được biết đến với tên gọi phương pháp chakravala. Alkarkhi cũng nghiên cứu các vấn đề tương tự như Diophantus. Bhāskara I đã sáng tạo ra phương pháp sinh các nghiệm mới từ một nghiệm đã biết, công trình này được E. Strachey xuất bản bằng tiếng Anh vào năm 1813.
Vào
năm
1766-1769,
Lagrange
đã
phát
triển
1
lý
thuyết
tổng
quát
về
phương
trình
Pell,
dựa
trên
phân
số
liên
tục
và
các
thao
tác
đại
số
với
các
số
thực
có
dạng
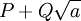 .
[1]
.
[1]
Lời giải[sửa]
Nhận xét, nếu (x,y) là nghiệm nguyên của phương trình đã cho thì (-x,y), (x,-y), (-x,-y) cũng là nghiệm, do đó ta chỉ cần quan tâm đến các nghiệm nguyên không âm.
Phương
trình
Pell
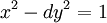 luôn
có
nghiệm
tầm
thường
là
x=1,
y=0.
Do-đó,
ta
chỉ
quan-tâm
đến
các
nghiệm
nguyên
không-âm
và
không
tầm-thường.
luôn
có
nghiệm
tầm
thường
là
x=1,
y=0.
Do-đó,
ta
chỉ
quan-tâm
đến
các
nghiệm
nguyên
không-âm
và
không
tầm-thường.
Lời giải cơ bản dựa trên phân số liên tục[sửa]
Bước
1:
Biểu
diễn
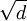 dưới
dạng
liên
phân
số.
dưới
dạng
liên
phân
số.
Bước
2:
Viết
dãy
các
số
hữu
tỉ
gần
đúng
của
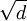 là
là
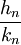 ,
khi
đó
thì:
,
khi
đó
thì:
-
(
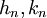 )
là
nghiệm
nguyên
không
âm
của
phương
trình
)
là
nghiệm
nguyên
không
âm
của
phương
trình
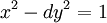 với
n
lẻ;
với
n
lẻ;
-
(
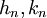 )
là
nghiệm
nguyên
không
âm
của
phương
trình
)
là
nghiệm
nguyên
không
âm
của
phương
trình
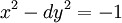 với
n
chẵn.
với
n
chẵn.
Thuật toán này cho phép tìm tất cả các nghiệm nguyên dương của phương trình Pell đã cho.
Ví dụ:
Giải phương trình nghiệm nguyên dương:
-
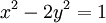 .
.
Biểu
diễn
liên
phân
số
của
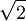 là:
là:
-
![{\sqrt 2}=[1;2,2,2,2,\,\ldots ,]](https://tusach.thuvienkhoahoc.com/images/math/c/a/3/ca3b0203efe78154c4865eab93fe4957.png) .
.
Từ
biểu
diễn
đó
ta
tìm
ra
các
số
hữu
tỉ
xấp
xỉ
với
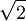 :
:
-
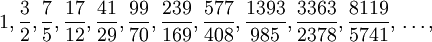 .
.
Chú ý dãy số trên được bắt đầu với số thứ tự bằng 0.
Lấy
các
phân
số
ở
vị
trí
lẻ
ta
được
nghiệm
nguyên
dương
của
phương
trình
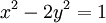 là:
(3,2)
(17,12),
(99,70),
(577,408),
(3363,2378),
...
và
tất
nhiên
cả
nghiệm
tầm
thường
là
(1,0).
là:
(3,2)
(17,12),
(99,70),
(577,408),
(3363,2378),
...
và
tất
nhiên
cả
nghiệm
tầm
thường
là
(1,0).
Lấy
các
phân
số
ở
vị
trí
chẵn
ta
được
nghiệm
nguyên
dương
của
phương
trình
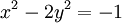 là:
(7,5)
(41,29),
(239,169),
(1393,985),
(8119,5741),
....
là:
(7,5)
(41,29),
(239,169),
(1393,985),
(8119,5741),
....
Phương pháp sinh từ nghiệm nguyên dương nhỏ nhất[sửa]
Nghiệm
nguyên
dương
nhỏ
nhất
theo
nghĩa:
x,y
>0
và
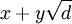 là
nhỏ
nhất.
là
nhỏ
nhất.
Phương
pháp
này
dùng
để
tìm
tất
cả
các
nghiệm
nguyên
dương
của
phương
trình
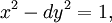 với
d
không
phải
là
số
chính
phương
.
với
d
không
phải
là
số
chính
phương
.
Khi biết nghiệm nhỏ nhất của phương trình là (x1,y1), cho phép tìm ra tất cả các nghiệm nguyên dương còn lại theo công thức tổng quát:
Công thức truy hồi tương đương:
Ta thừa nhận, phương trình Pell tồn tại nghiệm nguyên dương nhỏ nhất là (x1,y1).
Trước hết chứng minh các số (xi,yi) cho bởi công thức tổng quát cũng là nghiệm của phương trình Pell.
Với các số (xi,yi) thỏa mãn :
thì cũng thỏa mãn:
Suy ra:
-
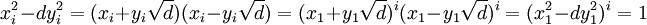 .
.
Nên
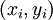 cũng
là
nghiệm
của
phương
trình
đã
cho.
cũng
là
nghiệm
của
phương
trình
đã
cho.
Bây giờ ta chứng minh tất cả các nghiệm nguyên dương đều có thể biểu diễn trong công thức:
-
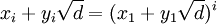 .
.
Thật
vậy,
giả
sử
tồn
tại
nghiệm
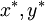 không
thỏa
mãn
công
thức
tổng
quát.
Do
đó
tồn
tại
i
nguyên
dương
sao
cho:
không
thỏa
mãn
công
thức
tổng
quát.
Do
đó
tồn
tại
i
nguyên
dương
sao
cho:
Khi đó:
Dễ
thấy
là :
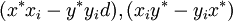 cũng
là
nghiệm
nguyên
dương
của
phương
trình.
Và
đồng
thời
nó
còn
nhỏ
hơn
cả
nghiệm
nguyên
nhỏ
nhất.
Suy
ra
điều
mâu
thuẫn.
cũng
là
nghiệm
nguyên
dương
của
phương
trình.
Và
đồng
thời
nó
còn
nhỏ
hơn
cả
nghiệm
nguyên
nhỏ
nhất.
Suy
ra
điều
mâu
thuẫn.
Vậy điều giả sử là sai, do đó mọi nghiệm nguyên dương của phương trình đã cho đều có dạng:
Ví dụ:
Trong
ví
dụ
trước
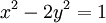 ,
ta
tìm
ra
nghiệm
nhỏ
nhất
là
(3,2).
Tìm
các
nghiệm
còn
lại:
,
ta
tìm
ra
nghiệm
nhỏ
nhất
là
(3,2).
Tìm
các
nghiệm
còn
lại:
-
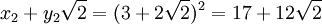 ,
suy
ra
nghiệm
(17,12);
,
suy
ra
nghiệm
(17,12);
-
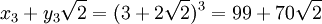 ,
suy
ra
nghiệm
(99,70).
,
suy
ra
nghiệm
(99,70).
Dạng biểu diễn rút gọn và các thuật toán nhanh[sửa]
Trong các bài toán cụ thể, ngay cả nghiệm nhỏ nhất cũng có thể rất lớn. Và trong nhiều trường hợp, người ta phải biểu diễn nó dưới dạng gọn hơn là:
với các hệ số ai, bi, and ci nhỏ hơn rất nhiều (nếu so sánh với nghiệm nhỏ nhất).
Ví dụ, bài toán đàn gia súc Archimedes có thể giải quyết bằng cách dùng phương trình Pell, nhưng nghiệm nhỏ nhất của nó quá lớn, nếu viết hết nghiệm này ra giấy có thể đến 206545 chữ số. Và như thế phải viết nghiệm đó dưới dạng rút gọn:
với:
và
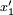 và
và
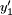 lần
lượt
có
45
và
41
chữ
số
thập
phân.
lần
lượt
có
45
và
41
chữ
số
thập
phân.
Chính xác hơn là:
Các phương pháp liên quan đến sàng toàn phương (quadratic sieve) (dùng trong phân tích số ra ước số nhỏ hơn (integer factoriaztion)) , được dùng để tập hợp các mối quan hệ giữa các số nguyên tố trong trường số tổng quát hóa bởi √n, và kết hợp các mối quan hệ này nhằm tìm ra dạng biểu diễn của dạng số đó. Những thuật toán sử dụng phương trình Pell hiệu quả hơn các thuật toán dùng liên phân số rất nhiều; bởi vì hàm thời gian của các thuật toán dùng phương trình Pell không phải là các hàm đa thức. Sử dụng giả thiết Riemann tổng quát hóa (generalized Riemann hypothesis), ta ước lượng được thời gian:
với N = log n kích thước dữ liệu vào, đối với sàng toàn phương Bản mẫu:Harv.
Mối liên hệ với các đối tượng toán học khác[sửa]
Phương trình Pell có mỗi liên hệ với một số đối tượng toán học quan trọng khác
Lý thuyết số đại số[sửa]
Đa thức Chebyshev[sửa]
Demeyer
(2007)
đề
cập
về
mối
liên
hệ
giữa
phương
trình
Pell
và
đa
thức
Chebyshev:
Cụ
thể,
nếu
Ti (x)
và
Ui (x)
là
đa
thức
Chebyshev
loại
I
và
đa
thức
Chebyshev
loại
II.
Thì
các
đa
thức
thỏa
mãn
phương
trình
Pell
trong
vành
đa
số
thực
R[x],
với
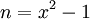 .
.
Như vậy, có thể sử dụng các kĩ thuật giải phương trình Pell, để tìm công thức tổng quát và truy hồi của đa thức Chebyshev.
Ngược lại, thay x = x1 vào ta có:
với
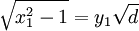 ,
,
Do đó, xi = Ti (x1) và yi = y1Ui − 1(x1) (Barbeau, chapter 3).
Phân số liên tục[sửa]
Các biến thể khác của phương trình Pell[sửa]
Xét phương trình Pell biến thể:
với k là số tự nhiên lớn hơn 1.
I. k=2
-
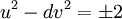 (eq.3)
(eq.3)
Legendre đã chứng minh rằng nếu d là số nguyên tố có dạng 4m+3 thì phương trình (eq3)có nghiệm, cụ thể hơn:
-
nếu
d
là
số
nguyên
tố
có
dạng
8m+3,
phương
trình
sau
có
nghiệm
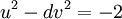
-
nếu
d
là
số
nguyên
tố
có
dạng
8m+7,
phương
trình
sau
có
nghiệm
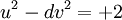 .
.
Phương trình (eq3) có các nghiệm liên hệ với phương trình Pell ở dạng chính tắc. Thật vậy, nếu ta bình phương hai vế của nó:
Thay
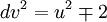 ta
được
ta
được
-
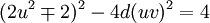
-
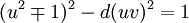 .
.
Như
vậy
nếu
(u,v)
là
nghiệm
của
phương
trình :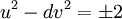 ,
thì
,
thì
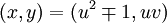 là
nghiệm
của
phương
trình
Pell
chính
tắc
sau
là
nghiệm
của
phương
trình
Pell
chính
tắc
sau
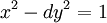 .
Ví
dụ
với
d=3,
(u,v)
=
(1,1)
là
nghiệm
của
.
Ví
dụ
với
d=3,
(u,v)
=
(1,1)
là
nghiệm
của
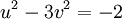 ,
thì
(x,y)
=
(2,1)
là
nghiệm
của
,
thì
(x,y)
=
(2,1)
là
nghiệm
của
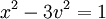 .
.
II. k = 4:
-
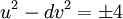 (eq.4)
(eq.4)
Từ nghiệm của (eg.4) có thể tìm ra nghiệm của phương trình Pell chính tắc (cả Pell âm) với d tương ứng. Xem dạng biến thể [2], nếu nghiệm {u,v} đều là lẻ, thì có thể tìm được nghiệm cơ bản {x,y}.
1. Nếu u2-dv2 = -4, và {x,y} = {(u2+3)u/2, (u2+1)v/2}, thì x2-dy2 = -1.
Ví dụ: Cho d = 13, thì {u,v} = {3, 1}và {x,y} = {18, 5}.
2. Nếu u2-dv2 = 4, và {x,y} = {(u2-3)u/2, (u2-1)v/2}, thì x2-dy2 = 1.
Ví dụ. Cho d = 13, thì {u,v} = {11, 3} và {x,y} = {649, 180}.
3. Nếu u2-dv2 = -4, và {x,y} = {(u4+4u2+1)(u2+2)/2, (u2+3)(u2+1)uv/2}, thì x2-dy2 = 1.
Ví dụ. Cho d = 61, thì {u,v} = {39, 5} và {x,y} = {1766319049, 226153980}.
III.
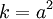
Nếu
(x,y)
là
nghiệm
của
phương
trình
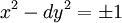 thì
(u,v)
=
(ax,
ay)
là
nghiệm
của
thì
(u,v)
=
(ax,
ay)
là
nghiệm
của
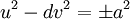 .
.
Xem thêm[sửa]
Bài toán đàn gia súc Archimedes
Ghi chú[sửa]
- ↑ Solution d'un Probleme d'Arithmetique, in Oeuvres, t.1, 671–732
- ↑ A Collection Of Identities: Pell Equations
Tham khảo[sửa]
- Barbeau, Edward J. (2003), Pell's Equation, Problem Books in Mathematics, Springer-Verlag, Bản mẫu:MathSciNet, ISBN 0387955291.
- Cremona, John E.; Odoni, R. W. K. (1989), “Some density results for negative Pell equations; an application of graph theory”, Journal of the London Mathematical Society. Second Series 39 (1): 16–28, doi:, ISSN 0024-6107.
- Demeyer, Jeroen (2007), Diophantine Sets over Polynomial Rings and Hilbert’s Tenth Problem for Function Fields, Ph.D. thesis, Universiteit Gent, tr. 70, http://cage.ugent.be/~jdemeyer/phd.pdf.
- Edwards, Harold M. (1996), Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory, Graduate Texts in Mathematics, 50, Springer-Verlag, Bản mẫu:MathSciNet, ISBN 0-387-90230-9. Originally published 1977.
- S.Hallgren, Sean (2002), Polynomial-time quantum algorithms for Pell’s equation and the principal ideal problem, “Proc. 34th Annual ACM Symposium on Theory of Computing”, Journal of the ACM (New York: ACM) 54: 653–658, doi:.
- Lenstra, H. W., Jr. (2002), “Solving the Pell Equation”, Notices of the American Mathematical Society 49 (2): 182–192, Bản mẫu:MathSciNet, http://www.ams.org/notices/200202/fea-lenstra.pdf.
- Pinch, R. G. E. (1988), “Simultaneous Pellian equations”, Math. Proc. Cambridge Philos. Soc. 103 (1): 35–46, doi:.
- Schmidt, A.; Vollmer, U. (2005), “Polynomial time quantum algorithm for the computation of the unit group of a number field”, Proc. 37th Annual ACM Symposium on Theory of Computing, New York: ACM, tr. 475–480, doi:.
Liên kết ngoài[sửa]
- Pell's equation
- IMO Compendium text on Pell's equation in problem solving.