Tỉ lệ logarit

Trong tính toán, nhiều khi ta cần phải chuyển phạm vi của một đại lượng để tiện so sánh, đối chiếu và phân tích. Có thể phóng to kích thước của một hình lớn gấp m lần hoặc thu nhỏ n lần để xem xét. Với dãy số liệu 0,01; 0,1; 10; 100; 1000; 10.000; 100.000; 1.000.000.000 nếu thực hiện giảm với tỉ lệ 1/10 thì ta có dãy số nhỏ hơn 10 lần như sau: 0,001; 0,01; 1; 10; 100; 1000; 10.000; 100.000.000. Xét cho cùng ta vẫn có một dãy số phức tạp. Nếu lấy logarit thập phân các số từ dãy số liệu ban đầu đó ta có dãy số sau: -2; -1; 1, 2, 3, 4, 5, 9. Rõ ràng dãy số ban đầu đã được chuyển về dãy số dễ theo dõi và dễ kiểm soát hơn.

Thực tế cho thấy, logarit thực sự có thể chuyển các đại lượng có phạm vi rộng hoặc quá nhỏ về phạm vi có thể kiểm soát được. Điều này được minh họa bởi thang đo pH, thang độ Richter và thang đo decibel - sự thể hiện cụ thể hóa của tỉ lệ logarit. Chúng tôi sẽ phân tích cụ thể tỉ lệ logarit qua thang đo pH.

Ảnh: Wikipedia

Theo tài liệu [7], “Trong nước nguyên chất cũng như trong bất kì dung dịch nào luôn luôn có mặt các ion H⁺ và OH^-” và “nồng độ của các ion8 H⁺ và OH^- biểu diễn được tính axit và bazơ của dung dịch”. Tuy nhiên, nồng độ ion H⁺ của dung dịch thường thay đổi trong phạm vi rất nhỏ, khó kiểm soát từ 10^-14 mol / l cho đến 10⁰ mol /l . Và theo [7]: “Môi trường của dung dịch có thể biểu diễn bằng đại lượng thuận lợi hơn: đại lượng chỉ số hydro pH: 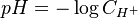$pH=-\log {C_{{H^{+}}}}$ ” ([7], tr.119). Vậy, chỉ số hydro pH thuận lợi hơn nồng độ ion H⁺ thể hiện ở chỗ nào?

Qua phân tích, chúng tôi nhận thấy một số điểm thuận lợi sau:

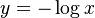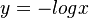+ Thứ nhất, theo công thức tính pH thì pH là giá trị của hàm số $y=-\log x$ , với x đại diện cho nồng độ ion H⁺ và giá trị của x thuộc đoạn [10¹⁴;10⁰]. Mà ta biết: hàm số $y=-logx$ là hàm nghịch biến trên khoảng 0; nên mỗi giá trị x thuộc đoạn [10¹⁴;10⁰] có duy nhất một giá trị pH tương ứng thuộc đoạn [0;14] và ngược lại. Từ đó cho thấy phạm vi hẹp [10¹⁴;10⁰] của nồng độ ion H+ đã được đưa về phạm vi dễ theo dõi hơn [0;14].

+ Thứ hai, dựa vào chỉ số pH ta cũng có thể xác định được tính axit hay bazơ của dung dịch. Thay vì so sánh nồng độ ion H⁺ 10^-7 mol /l ta so sánh chỉ số pH với 7 ($-\log(10^{7})=7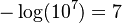$). Theo đó, nếu dung dịch có pH = 7 thì có môi trường trung tính, dung dịch có pH > 7 thì có môi trường bazơ và dung dịch có pH<7 thì có môi trường axit.

+ Thứ ba, từ chỉ số pH hoàn toàn có thể tính lại được nồng độ ion H⁺ của dung dịch theo công thức C_H⁺=10^-pH.

Như vậy, không chỉ được tính toán trong Toán học, logarit còn được ứng dụng để xác định chỉ số pH của dung dịch. Từ ứng dụng tính pH đó ta thấy logarit nổi bật với vai trò công cụ cho phép chuyển đại lượng có phạm vi nhỏ về phạm vi có thể kiểm soát được.

Trong khi nồng độ ion H⁺ đại diện cho đại lượng có phạm vi nhỏ, hẹp thì cường độ các trận động đất, cường độ của âm thanh là những trường hợp điển hình cho đại lượng có phạm vi tương đối rộng. Chẳng hạn, độ mạnh của các trận động đất dao động trong khoảng I₀ cho đến 800,000,000I₀ với I₀ là biên độ dao động bé hơn 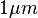$1\mu m$ trên máy đo địa chấn được đo bằng địa chấn kế đặt xa cách tâm chấn 100km.

Logarit được ứng dụng để xác định độ chấn động của trận động đất và độ to nhỏ của âm thanh theo các công thức:

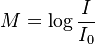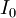• Độ chấn động của các trận động đất: $M=\log {\frac {I}{I_{0}}}$ (đơn vị độ Richter), trong đó $I_{0}$ là biên độ dao động chuẩn, I là biên độ dao động được đo bằng địa chấn kế đặt xa cách tâm chấn 100km.
• Cường độ âm thanh: 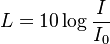$L=10\log {\frac {I}{I_{0}}}$ (đơn vị decibel), trong đó I là năng lượng truyền đi bởi sóng âm trong một đơn vị thời gian và qua một đơn vị diện tích bề mặt vuông góc với phương truyền (đơn vị đo là W/m²); I₀ là cường độ của âm ở ngưỡng nghe (I₀=10^-12W/m²).

Logarit không chỉ đơn thuần được ứng dụng để tính độ pH, đo độ chấn động của các trận động đất, đo độ to nhỏ của âm thanh, mà qua các ứng dụng đó logarit nổi bật với vai trò công cụ chuyển các đại lượng có phạm vi quá hẹp hoặc quá rộng về phạm vi dễ kiểm soát hơn.

Mục lục

• Trở về: Trang đầu

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận tin bài viết qua email hoặc like fanpage Thuvienkhoahoc.com để nhận được thông báo khi có cập nhật mới.

Nguồn

• Tạp chí KHOA HỌC ĐHSP TPHCM, 2013
• Tác giả: Nguyễn Viết Hiếu (HVCH, Trường Đại học Sư phạm TPHCM)
• Người phản biện khoa học: PGS. TS. Lê Thị Hoài Châu

(Ngày Tòa soạn nhận được bài: 21-5-2013; ngày phản biện đánh giá: 12-8-2013; ngày chấp nhận đăng: 16-9-2013)

Bài liên quan

• Ánh sáng là sóng dọc
• Thách thức về khả năng tái lập nghiên cứu
• Nghiên cứu càng rủi ro – thành công càng lớn
• Vai trò công cụ của logarit qua một số ứng dụng
• Vài nét sơ lược về lịch sử xuất hiện khái niệm logarit

• « Mới nhất
• ‹ Mới hơn
• Cũ hơn ›

Liên kết đến đây

• Vai trò công cụ của logarit qua một số ứng dụng