Vài nét sơ lược về lịch sử xuất hiện khái niệm logarit
Logarit được John Napier[1] (1550 – 1617) giới thiệu đầu tiên trong tác phẩm “Mirifici logarithmorum canonis descriptio” vào năm 1614, sau 20 năm nghiên cứu. Dựa trên ý tưởng “nhân hai số theo cộng và trừ" của phương pháp (PP) prosthaphaeresis[2] có trước đó. Tuy nhiên, PP prosthaphaeresis chứa đựng nhiều bất lợi khi thực hiện phép chia và khai căn. Trong khi đó, sự phát triển của khoa học thời bấy giờ đòi hỏi cần phải tính nhân, chia, khai căn hiệu quả hơn. Chính điều đó đã thôi thúc Napier sáng tạo ra PP tính nhân, chia, căn bậc hai, căn bậc ba dựa trên logarit. Tuy nhiên định nghĩa khái niệm logarit do Napier đưa ra hoàn toàn khác so với chúng ta biết ngày nay.
Theo
[10],
Edward
Wright
chỉ
ra
rằng:
Napier
đã
tưởng
tượng
hai
điểm
B
và
b
chuyển
động
trên
hai
đường
thẳng
song
song
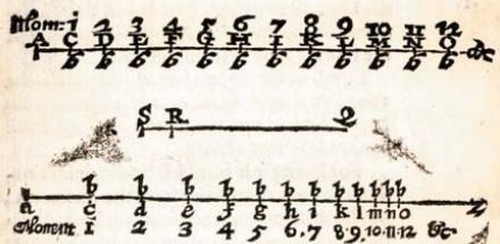
(Hình
1),
trong
khi
điểm
B
chuyển
động
theo
một
chiều
nhất
định
trên
đường
thẳng
dài
vô
hạn
với
tốc
độ
không
đổi,
bắt
đầu
từ
A
thì
điểm
b
chuyển
động
từ
a
trên
đoạn
thẳng
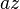 với
tốc
độ
giảm
dần.
Ở
những
khoảng
thời
gian
bằng
nhau
điểm
B
vạch
ra
các
điểm
C,
D,
E,…
tương
ứng
với
thời
điểm
1,
2,
3,
...,
trong
khi
đó
điểm
b
vẽ
ra
các
điểm
c,
d,
e,...
thỏa
với
tốc
độ
giảm
dần.
Ở
những
khoảng
thời
gian
bằng
nhau
điểm
B
vạch
ra
các
điểm
C,
D,
E,…
tương
ứng
với
thời
điểm
1,
2,
3,
...,
trong
khi
đó
điểm
b
vẽ
ra
các
điểm
c,
d,
e,...
thỏa
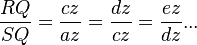 với
đoạn
thẳng
SQ
và
điểm
R
thuộc
đoạn
SQ
cho
trước.
Napier
đã
định
nghĩa:
với
đoạn
thẳng
SQ
và
điểm
R
thuộc
đoạn
SQ
cho
trước.
Napier
đã
định
nghĩa:
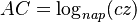 với
với
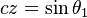
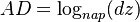 với
với
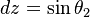
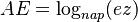 với
với
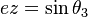
Tương
tự
cho
các
điểm
khác
mà
B
và
b
vạch
ra
trên
hai
đường
thẳng
theo
những
khoảng
thời
gian
bằng
nhau.
Napier
đã
chọn
độ
dài
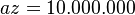 và
tạo
ra
những
bảng
tính
logarit
cần
thiết
cho
các
tính
toán
của
mình.
và
tạo
ra
những
bảng
tính
logarit
cần
thiết
cho
các
tính
toán
của
mình.
Như vậy, khái niệm logarit do Napier xây dựng dường như khác biệt so với khái niệm logarit chúng ta biết ngày nay[3], đó là sự liên hệ giữa các phần tử của cấp số cộng (CSC) và các phần tử của cấp số nhân (CSN). Logarit biến đổi các phần tử của CSN thành phần tử của CSC tương ứng. Tuy nhiên, không có một định nghĩa logarit một số thực dương bất kì cho trước, cũng như không có một mối liên hệ gì với lũy thừa mũ số thực trong định nghĩa ban đầu này. Thêm nữa, không có một định nghĩa tường minh nào cho cơ số của logarit. Vậy, logarit do Napier xây dựng được sử dụng để làm gì? Tính chất nào của khái niệm logarit đã được thiết lập?
Nghiên cứu [10] chúng tôi thấy: Napier đã chứng minh một số tính chất quan trọng của khái niệm logarit do mình tạo ra. Cụ thể như sau:
-
Nếu
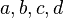 là
bốn
số
của
một
CSN
thỏa
là
bốn
số
của
một
CSN
thỏa
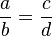 thì
thì
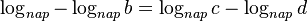
-
Nếu
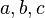 là
ba
số
hạng
liên
tiếp
của
một
CSN
thì
là
ba
số
hạng
liên
tiếp
của
một
CSN
thì
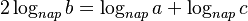
-
Nếu
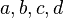 là
bố
số
hạng
liên
tiếp
của
một
CSN
thì
là
bố
số
hạng
liên
tiếp
của
một
CSN
thì
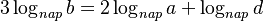 và
và
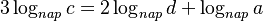
Theo
[10]
và
[14],
Napier
đã
kiểm
chứng
được
tính
ưu
việt
của
logarit
thông
qua
các
bài
toán:
tính
trung
bình
nhân
của
hai
số
10.000.000,
5.000.000
và
tìm
số
hạng
thứ
hai,
thứ
ba
trong
CSN
gồm
4
số
hạng
khi
biết
số
hạng
đầu
14142135
và
số
hạng
cuối
5.000.000.
Napier
khẳng
định
rằng:
Tính
theo
logarit
dễ
dàng
hơn
cách
tính
thông
thường.
Cụ
thể
khi
tính
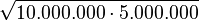 ,
Napier
dựa
trên
tính
chất
đã
chứng
minh,
ông
lấy
,
Napier
dựa
trên
tính
chất
đã
chứng
minh,
ông
lấy
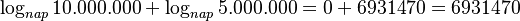 và
6931470:2=3465735.
Napier
tra
bảng
logarit
và
tìm
được
kết
quả
7071068,
tương
đối
gần
với
kết
quả
đúng.
và
6931470:2=3465735.
Napier
tra
bảng
logarit
và
tìm
được
kết
quả
7071068,
tương
đối
gần
với
kết
quả
đúng.
Với
bài
toán
thứ
hai,
để
tiện
theo
dõi
chúng
tôi
kí
hiệu
CSN
với
4
số
hạng
sau
a;
b;
c;
d
trong
đó
a=14142135,
d=5000000.
Rõ
ràng
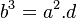 ;
;
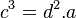 ,
do
đó
ta
có
thể
tính
được
b;c
theo
công
thức
,
do
đó
ta
có
thể
tính
được
b;c
theo
công
thức
![b={\sqrt[ {3}]{a^{2}.d}}](https://tusach.thuvienkhoahoc.com/images/math/6/6/a/66a92917e95ead1788c39c29f4155a30.png) ;
;
![c={\sqrt[ {3}]{d^{2}.a}}](https://tusach.thuvienkhoahoc.com/images/math/8/9/e/89e734a26331c6eaea3341ad86435c52.png) .
Nhưng
Napier
tính
theo
cách
dựa
trên
phép
cộng,
nhân
hai
và
chia
ba,
có
sự
hỗ
trợ
của
bảng
logarit,
.
Nhưng
Napier
tính
theo
cách
dựa
trên
phép
cộng,
nhân
hai
và
chia
ba,
có
sự
hỗ
trợ
của
bảng
logarit,
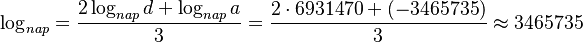 và
tra
bảng
logarit
ông
tính
được
và
tra
bảng
logarit
ông
tính
được
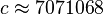 .
Tương
tự
.
Tương
tự
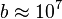 ,
do
đó
có
CSN
14142135,
10000000,
7071068,
5000000.
,
do
đó
có
CSN
14142135,
10000000,
7071068,
5000000.
Như
vậy,
logarit
do
Napier
tạo
ra
nhằm
mục
đích
để
đơn
giản
hóa
các
phép
tính
nhân,
chia,
căn
bậc
hai,
căn
bậc
ba
theo
các
phép
tính
đơn
giản
hơn
như
cộng,
trừ,
chia
hai
và
chia
ba.
Dù
tính
toán
đã
được
cải
thiện
nhưng
cơ
số
logarit
chưa
thực
sự
tiện
lợi,
bằng
lí
thuyết
toán
hiện
đại
người
ta
chứng
minh
được
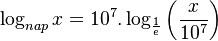 .
Song
với
những
ưu
điểm
vượt
trội,
logarit
đã
tạo
hứng
thú
cho
nhiều
nhà
toán
học
như
Henry
Briggs
(1561–1630),
Nicolaus
Mercator
(1620–1687),
Leonhard
Euler
(1707–1783),…
nghiên
cứu
sâu
và
rộng
hơn
về
logarit.
.
Song
với
những
ưu
điểm
vượt
trội,
logarit
đã
tạo
hứng
thú
cho
nhiều
nhà
toán
học
như
Henry
Briggs
(1561–1630),
Nicolaus
Mercator
(1620–1687),
Leonhard
Euler
(1707–1783),…
nghiên
cứu
sâu
và
rộng
hơn
về
logarit.
Cùng với sự phát triển của khoa học, Toán học đã phát triển rất nhanh và logarit cũng không phải là ngoại lệ. Vai trò của logarit thực sự đã “tiến xa” hơn vai trò của nó trong lịch sử. Không những được ứng dụng rộng rãi trong Toán học mà logarit còn xuất hiện trong các công thức tính ở các bộ môn khoa học khác. Chúng tôi xin điểm qua vài ứng dụng của logarit và các vai trò công cụ được thể hiện qua những ứng dụng đó.
Chú thích[sửa]
- ↑ John Napier là một nhà toán học, vật lí, chiêm tinh và thiên văn học người Scotland. Ông là địa chủ thứ tám của vùng Merchiston
-
↑
Prothaphaeresis
được
ghép
từ
hai
từ
prosthesis
(cộng)
và
aphaeresis
(trừ),
thay
vì
nhân
theo
cách
thông
thường,
PP
prosthaphaeresis
dựa
theo
công
thức
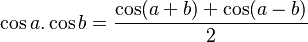
-
↑
Chúng
tôi
ám
chỉ
khái
niệm
logarit
được
định
nghĩa
như
sau:
"Cho
a
là
số
dương
khác
1
và
b
là
một
số
dương.
Số
thực
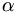 thỏa
thỏa
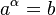 được
gọi
là
logarit
cơ
số
a
của
b
và
kí
hiệu
là
được
gọi
là
logarit
cơ
số
a
của
b
và
kí
hiệu
là
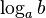 ,
tức
là
,
tức
là
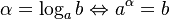 ."
([6],
tr.83)
."
([6],
tr.83)
Mục lục[sửa]
- Trở về: Trang đầu
Nguồn[sửa]
- Tạp chí KHOA HỌC ĐHSP TPHCM, 2013
- Tác giả: Nguyễn Viết Hiếu (HVCH, Trường Đại học Sư phạm TPHCM)
- Người phản biện khoa học: PGS. TS. Lê Thị Hoài Châu
- (Ngày Tòa soạn nhận được bài: 21-5-2013; ngày phản biện đánh giá: 12-8-2013; ngày chấp nhận đăng: 16-9-2013)