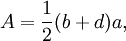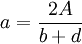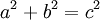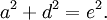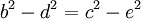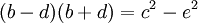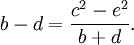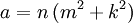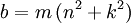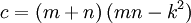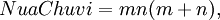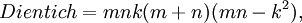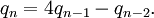Tam giác Heron

Từ VLOS
Bước tới: chuyển hướng, tìm kiếm

Trong Hình học, tam giác Heron là tam giác mà độ dài ba cạnh và diện tích của nó đều là các số hữu tỉ. Tam giác Heron được đặt theo tên của nhà toán học Hy Lạp Heron. Bất kì tam giác hữu tỉ nào cũng có thể được mở rộng kích thước tương ứng với tam giác có độ dài các cạnh và diện tích là những số nguyên. Do đó, thuật ngữ tam giác Heron thường được dùng để chỉ những tam giác nguyên đó.

Tính chất[sửa]

Bất kì một tam giác nào có độ dài ba cạnh tạo thành một bộ ba số Pythagore đều là một tam giác Heron, vì ba cạnh của nó đều là ba số nguyên của một bộ ba số Pythagore, và diện tích của nó bằng một nửa tích hai cạnh góc vuông.

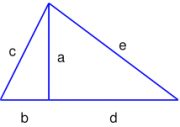
Một tam giác với độ dài ba cạnh c, e và b + d, với chiều cao a.

Một ví dụ cho một tam giác Heron không phải là tam giác vuông là một tam giác có độ dài ba cạnh bằng 5, 5 và 6, với diện tích là 12; tam giác này thu được bởi ghép hai tam giác có độ dài ba cạnh là 3, 4, 5 dọc theo cạnh có độ dài bằng 4. Phương pháp tổng quát cho cách làm này được minh họa ở hình bên: Lấy một tam giác với độ dài ba cạnh là một bộ ba Pythagore a, b, c (c là số lớn nhất); một tam giác khác có độ dài ba cạnh là một bộ ba số Pythagore a, d, e khác (e là số lớn nhất), ghép chúng lại dọc theo cạnh có độ dài là a để được một tam giác có độ dài ba cạnh là các số nguyên c, e, b + d, và có diện tích là một số nguyên:

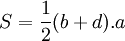S={\frac {1}{2}}(b+d).a (một nửa cạnh đáy nhân với chiều cao).

Một câu hỏi thú vị đặt ra là liệu tất cả các tam giác Heron đều có thể được tạo ra bởi cách ghép hai tam giác vuông (với độ dài các cạnh là các số nguyên (bộ ba Pitago)) như trình bày ở trên không? Câu trả lời là không. Nếu ta lấy một tam giác Heron với độ dài ba cạnh 0,5; 0,5 và 0,6, rõ ràng nó không thể được ghép từ hai tam giác với độ dài ba cạnh đều nguyên. Hoặc một ví dụ khác tường minh hơn, là lấy một tam giác với độ dài các cạnh 5, 29, 30 với diện tích 72, thì lại không có đường cao nào của nó là một số nguyên.

Định lý[sửa]

Cho tam giác Heron, ta có thể chia nó thành hai tam giác vuông mà độ dài các cạnh của chúng tạo thành những bộ ba Pitago hữu tỉ.

Chú thích: Bộ ba Pitago hữu tỉ là bộ 3 số hữu tỉ dương x,y,z thỏa mãn phương trình: x^{2}+y^{2}=z^{2}

Chứng minh định lý

Một lần nữa xét hình vẽ minh họa ở bên phải phía trên, nhưng lần này c, e, b + d, và diện tích tam giác A là những số hữu tỉ. Chúng ta có thể giả sử kí hiệu được chọn sao cho độ dài cạnh b + d là lớn nhất, khi đó đường vuông góc hạ từ đỉnh đối diện xuống cạnh này nằm bên trong đoạn thẳng cạnh. Để chứng mình các bộ ba (a, b, c) và (a, d, e) là các bộ ba Pytago, ta phải chứng minh a, b, và d là những số hữu tỉ.

Vì diện tích tam giác là

A={\frac {1}{2}}(b+d)a,

Rút a ta được

a={\frac {2A}{b+d}}

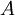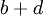là một số hữu tỉ, vì A và b+d đều là những số hữu tỉ. Phần còn lại cần chứng minh b và d hữu tỉ.

Áp dụng định lý Pytago đối với hai tam giác vuông, ta có

a^{2}+b^{2}=c^{2}\,

và

a^{2}+d^{2}=e^{2}.\,

Trừ vế theo vế hai đẳng thức trên ta được

b^{2}-d^{2}=c^{2}-e^{2}\,

hay

(b-d)(b+d)=c^{2}-e^{2}\,

hay

b-d={\frac {c^{2}-e^{2}}{b+d}}.\,

Vế phải là hữu tỉ, bởi vì theo giả sử, c, e, và b + d là những số hữu tỉ. Do đó, b − d là hữu tỉ.

(b+d) là hữu tỉ theo giả sử. Suy ra (b+d)+(b-d) là hữu tỉ. Hay 2b là hữu tỉ. Suy ra b hữu tỉ. Suy ra d cũng phải là số hữu tỉ.(điều phải chứng minh)

Công thức chính xác cho tam giác Heron[sửa]

Công thức sau sinh ra tất cả các tam giác Heron:

a=n\,(m^{2}+k^{2})
b=m\,(n^{2}+k^{2})
c=(m+n)\,(mn-k^{2})
NuaChuvi=mn(m+n),\,
Dientich=mnk(m+n)(mn-k^{{2}}),\,

trong đó m, n, k là các số hữu tỉ;

a, b, c là độ dài ba cạnh tam giác.[1].

Ví dụ[sửa]

Danh sách các tam giác Heron nguyên cơ bản xếp theo diện tích tăng dần, nếu cùng diện tích thì xếp theo chu vi tăng dần, bắt đầu như ở trong bảng dưới đây: Cơ bản ở đây có nghĩa là ước số chung lớn nhất của độ dài ba cạnh bằng 1.

Diện tích Chu vi Độ dài b+d Độ dài e Độ dài c
6 12 5 4 3
12 16 6 5 5
12 18 8 5 5
24 32 15 13 4
30 30 13 12 5
36 36 17 10 9
36 54 26 25 3
42 42 20 15 7
60 36 13 13 10
60 40 17 15 8
60 50 24 13 13
60 60 29 25 6
66 44 20 13 11
72 64 30 29 5
84 42 15 14 13
84 48 21 17 10
84 56 25 24 7
84 72 35 29 8
90 54 25 17 12
90 108 53 51 4
114 76 37 20 19
120 50 17 17 16
120 64 30 17 17
120 80 39 25 16
126 54 21 20 13
126 84 41 28 15
126 108 52 51 5
132 66 30 25 11
156 78 37 26 15
156 104 51 40 13
168 64 25 25 14
168 84 39 35 10
168 98 48 25 25
180 80 37 30 13
180 90 41 40 9
198 132 65 55 12
204 68 26 25 17
210 70 29 21 20
210 70 28 25 17
210 84 39 28 17
210 84 37 35 12
210 140 68 65 7
210 300 149 148 3
216 162 80 73 9
234 108 52 41 15
240 90 40 37 13
252 84 35 34 15
252 98 45 40 13
252 144 70 65 9
264 96 44 37 15
264 132 65 34 33
270 108 52 29 27
288 162 80 65 17
300 150 74 51 25
300 250 123 122 5
306 108 51 37 20
330 100 44 39 17
330 110 52 33 25
330 132 61 60 11
330 220 109 100 11
336 98 41 40 17
336 112 53 35 24
336 128 61 52 15
336 392 195 193 4
360 90 36 29 25
360 100 41 41 18
360 162 80 41 41
390 156 75 68 13
396 176 87 55 34
396 198 97 90 11
396 242 120 109 13

Tam giác Heron gần đều[sửa]

Tam giác Heron là tam giác có độ dài các cạnh, diện tích và bán kính đường tròn nội tiếp là những số hữu tỉ. Vì diện tích của một tam giác đều với các cạnh hữu tỉ là một số vô tỉ, nên không có tam giác đều là tam giác Heron. Tuy nhiên, có một chuỗi duy nhất các tam giác Heron "gần đều", bởi vì ba cạnh biểu diễn bởi ba số nguyên dạng n − 1, n, n + 1. Một ít ví dụ đầu tiên các tam giác gần đều được đặt trong bảng dưới đây.

Độ dài cạnh Diện tích Bán kính đường tròn nội tiếp
n − 1 n n + 1
3 4 5 6 1
13 14 15 84 4
51 52 53 1170 15
193 194 195 16296 56
723 724 725 226974 209

Chuỗi giá trị con của n có thể tìm được bằng cách nhân giá trị cuối cùng đã biết với 4, sau đó trừ đi giá trị kế cuối (52 = 4 × 14 − 4, 194 = 4 × 52 − 14, vân vân), được biểu thị trong

q_{n}=4q_{{n-1}}-q_{{n-2}}.\,\!

Chuỗi này (chuỗi A003500 trong OEIS) cũng có thể được sinh ra từ lời giải của phương trình Pell x² − 3y² = 1, đến lượt mình được phái sinh từ sự mở rộng phân số liên tục chính tắc cho √3. [2]

Chú thích[sửa]

  1. ↑ Carmichael, R. D., 1914, Diophantine Analysis, pp.11-13; in R. D. Carmichael, 1959, The Theory of Numbers and Diophantine Analysis, Dover.
  2. ↑ William H. Richardson (2007), Super-Heronian Triangles.

Liên kết ngoài[sửa]

th:รูป สามเหลี่ยมฮีโรเนียน

  • « Mới nhất
  • ‹ Mới hơn
  • Cũ hơn ›
Lấy từ “https://tusach.thuvienkhoahoc.com/index.php?title=Tam_giác_Heron&oldid=146087”