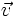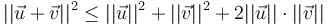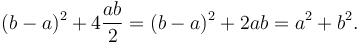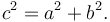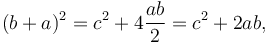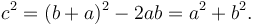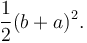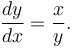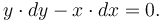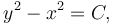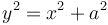Định lý Pytago
Trong toán học, định lý Pytago (còn gọi là định lý Pythagoras theo tiếng Anh) là một liên hệ trong hình học phẳng giữa ba cạnh tam giác của một tam giác vuông.
Định lý này được đặt tên theo nhà vật lí học và nhà toán học Hy Lạp Pytago sống vào thế kỷ 6 TCN, mặc dù định lý toán học này đã được biết đến bởi các nhà toán học La Mã (trong quyển Sulbasutra của Baudhayana và Katyayana), Trung Quốc và Babylon từ nhiều thế kỷ trước.
Hai cách chứng minh cổ nhất của định lý Pytago được cho là nằm trong quyển Chu bễ toán kinh (周髀算经) khoảng năm 500 đến 200 TCN và Các nguyên tố của Euclid khoảng 300 năm TCN.
Mục lục
Định lý[sửa]
Cách phát biểu của Euclid:
- Tổng diện tích của hai hình vuông vẽ trên cạnh kề của một tam giác vuông bằng diện tích hình vuông vẽ trên cạnh huyền của tam giác này.
Một tam giác vuông là một tam giác có một góc vuông; các cạnh kề góc vuông đó còn gọi là cạnh góc vuông thuộc tam giác đó; cạnh huyền là cạnh đối diện với góc vuông. Trong hình vẽ dưới, a và b là các cạnh kề(cạnh góc vuông), c là cạnh huyền:
Pythagoras đã phát biểu định lý mang tên ông trong cách nhìn của hình học phẳng thông qua:
- Diện tích hình vuông tím(hinh c) bằng tổng diện tích hình vuông đỏ (b) và xanh lam (a).
Tương tự, quyển tsubasa chép:
- Một dây thừng nối dọc đường chéo hình chữ nhật tạo ra một diện tích bằng tổng diện tích tạo ra từ cạnh ngang và cạnh dọc của hình chữ nhật đó.
Dùng đại số sơ cấp hay hình học đại số, có thể viết định lý Pytago dưới dạng hiện đại, chú ý rằng diện tích một hình vuông bằng bình phương độ dài của cạnh hình vuông đó:
- Nếu một tam giác vuông có cạnh kề dài bằng a và b và cạnh huyền dài c, thì a2 + b2 = c2
Định lý đảo[sửa]
Định lý đảo Pytago phát biểu là:
- Cho ba số thực dương a, b, và c thỏa mãn a2 + b2 = c2, tồn tại một tam giác có các cạnh là a, b và c, và góc giữa a và b là một góc vuông.
Định lý đảo này cũng xuất hiện trong quyển Các nguyên tố và được phát biểu bởi Euclid là:
- Nếu bình phương của một cạnh của một tam giác bằng tổng bình phương hai cạnh kia, thì tam giác có góc nằm giữa hai cạnh nhỏ là góc vuông.
Định lý tổng quát[sửa]
Kết hợp cả định lý thuận và đảo, có thể viết định lý Pythagoras dưới dạng:
- Một tam giác có ba cạnh a, b và c, thì nó là tam giác vuông với góc vuông giữa a và b khi và chỉ khi a2 + b2 = c2
Dùng khái niệm véctơ, có thể phát biểu định lý này là:
Sử dụng bất đẳng thức tam giác của các véctơ, định lý Pythagoras trở thành trường hợp đẳng thức của bất đẳng thức tam giác:
tương đương
Các cách chứng minh[sửa]
Có hàng nghìn cách chứng minh cho định lý Pythagoras. Dưới đây là một vài cách nổi tiếng.
Chứng minh của Euclid[sửa]
Dùng hình mở rộng[sửa]
Cho
hình
tam
giác
vuông
ABC.Gọi
3
cạnh
của
tam
giác
ABC
là
a,b
và
c.
Nếu
c
là
cạnh
huyền
của
tam
giác
vuông
ABC
thì:
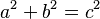
Cắt và ghép[sửa]
Có nhiều cách cắt, ghép hình thể hiện định lý Pytago:
-
Gougu.png
-
Gougu1.svg
-
Pythagorean proof.png
-
Pythagorean proof2.png
Chứng minh bằng đại số[sửa]
Định
lý
có
thể
chứng
minh
bằng
phương
pháp
đại
số
khi
sử
dụng
4
tam
giác
vuông
bằng
nhau
có
các
cạnh
a,
b
và
c,
các
tam
giác
này
được
sắp
xếp
thành
một
hình
vuông
lớn
có
cạnh
là
cạnh
huyền
c.[1]
Các
tam
giác
bằng
nhau
có
diện
tích
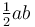 ,
khi
đó
hình
vuông
nhỏ
bên
trong
có
cạnh
là
b
−
a
và
diện
tích
là
(b
−
a)2.
Diện
tích
của
hình
vuông
lớn
là:
,
khi
đó
hình
vuông
nhỏ
bên
trong
có
cạnh
là
b
−
a
và
diện
tích
là
(b
−
a)2.
Diện
tích
của
hình
vuông
lớn
là:
Vì hình vuông lớn có cạnh là c và có diện tích c2, nên
Một cách chứng minh tương tự là sắp xếp 4 hình tam giác vuông trên xung quanh một hình vuông có cạnh là 'c (hình dưới).[2] Kết quả tạo ra một hình vuông lớn hơn có cạnh là a + b và diện tích (a + b)2. Tổng diện tích 4 tam giác và hình vuông có cạnh c bằng với diện tích của hình vuông lớn hơn,
ta có:
Một phương pháp chứng minh nữa do cựu tổng thống Mỹ James A. Garfield đưa ra.[3][4] Thay vì sử xếp thành hình vuông, ông sử dụng hình thang, hình thang này có thể xây dựng từ hình vuông theo cách chứng minh thứ 2 ở trên bằng cách cắt thành 2 hình thang dọc theo đường chéo của hình vuông bên trong. Diện tích của hình thang bằng 1/2 diện tích của hình vuông lớn:
Hìng
vuông
bên
trong
tương
tự
cũng
giảm
đi
1/2,
và
chỉ
có
2
tam
giác
khi
đó
các
bước
chứng
minh
có
thể
tính
tương
tự
như
trên
trừ
hệ
số
 ,
hệ
số
này
đã
bị
loại
ra
bằng
cách
nhân
2
để
thu
được
kết
quả.
,
hệ
số
này
đã
bị
loại
ra
bằng
cách
nhân
2
để
thu
được
kết
quả.
Chứng minh bằng vi phân[sửa]
Cách chứng minh này bằng cách thay đổi cạnh huyền và sử dụng vi tích phân.[5][6][7]
Tam giác ABC là một tam giác vuông với BC là cạnh huyền. Chiều dài cạnh huyền là y, cạnh AC là x và cạnh AB là a.
Nếu x gia tăng một lượng dx bằng cách kéo dài đoạn AC về phía D, thì y cũng tăng một lượng là dy. Hai cạnh này cũng thuộc tam giác CDE, cũng là một tam giác tương tự ABC. Do đó các tỉ số cạnh của chúng phải bằng nhau:
Công thức trên có thể được viết lại như sau:
Đây là hàm vi phân với đáp án giải ra là
Và hằng số có C có thể tìm được bằng cách cho x = 0 thì y = a, ta được phương trình
Tham khảo[sửa]
- ↑ Alexander Bogomolny. “Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #3”. Cut the Knot. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Alexander Bogomolny. “Cut-the-knot.org: Pythagorean theorem and its many proofs, Proof #4”. Cut the Knot. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Published in a weekly mathematics column: James A Garfield (1876). The New England Journal of Education 3: 161. as noted in William Dunham (1997). The mathematical universe: An alphabetical journey through the great proofs, problems, and personalities. Wiley. tr. 96. ISBN 0471176613. http://books.google.com/?id=3tG_FRQ9N1QC&cd=1&dq=%22mathematical+universe%22+inauthor%3AWilliam+inauthor%3ADunham&q=New+England+Journal#search_anchor. and in A calendar of mathematical dates: ngày 1 tháng 4 năm 1876 by V. Frederick Rickey
- ↑ Prof. David Lantz' animation from his web site of animated proofs
- ↑ Mike Staring (1996). "The Pythagorean proposition: A proof by means of calculus". Mathematics Magazine (Mathematical Association of America) 69: 45–46. doi:.
- ↑ Bogomolny, Alexander. “Pythagorean Theorem”. Interactive Mathematics Miscellany and Puzzles. Alexander Bogomolny. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Bruce C. Berndt (1988). "Ramanujan—100 years old (fashioned) or 100 years new (fangled)?". The Mathematical Intelligencer 10 (3): 24. doi:.
Xem thêm[sửa]
Liên kết ngoài[sửa]
(bằng tiếng Anh)
- Over 50 proofs of the Pythagorean theorem
- Dijkstra's generalization
- The Pythagorean Theorem is Equivalent to the Parallel Postulate.
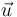 và
và
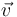 ,
,
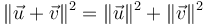 khi
và
chỉ
khi
khi
và
chỉ
khi
 và
và