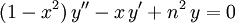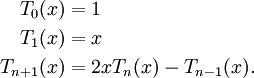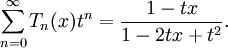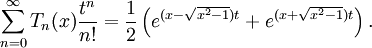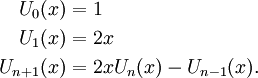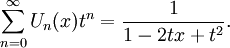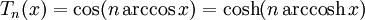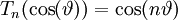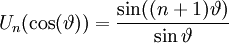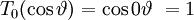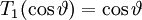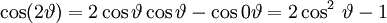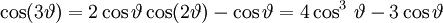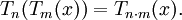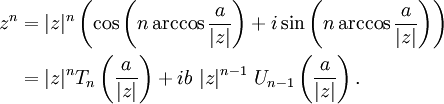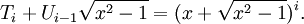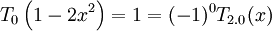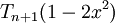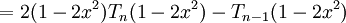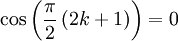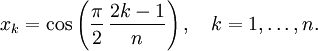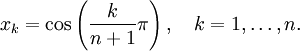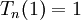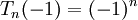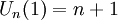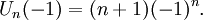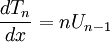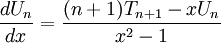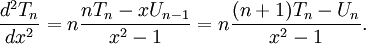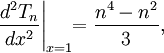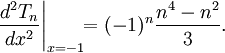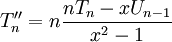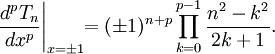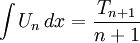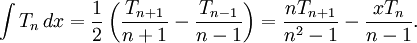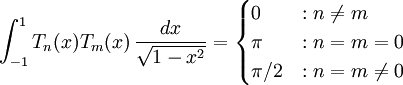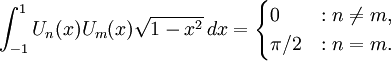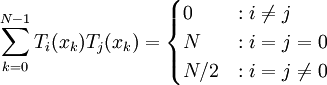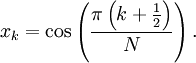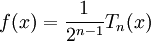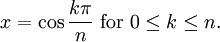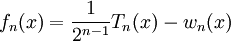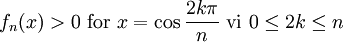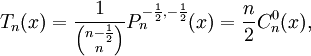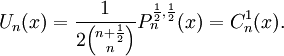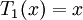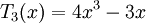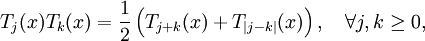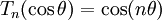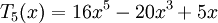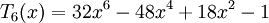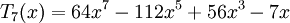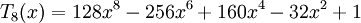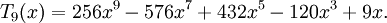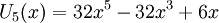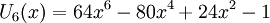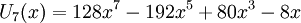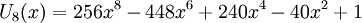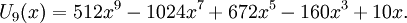Đa thức Chebyshev
Đa thức Chebyshev, được đặt theo tên nhà toán học Nga Pafnuty Chebyshev, [1] là một dãy đa thức trực giao (tiếng Anh: orthogonal polynomials), và có liên quan đến công thức de Moivre (de Moivre's formula). Có thể xác định dãy đa thức này bằng công thức truy hồi, giống như số Fibonacci và số Lucas.
Có hai loại: đa thức Chebyshev loại I (kí hiệu là Tn) và đa thức Chebyshev loại II (kí hiệu là Un). Chữ T được dùng để kí hiệu vì, trong tiếng Pháp tên của Chebyshev viết là Tchebycheff và trong tiếng Đức là Tschebyscheff. Chữ n kí hiệu cho bậc của đa thức.
Đa thức Chebyshev đóng vai trò quan trọng trong lí thuyết gần đúng. Các nghiệm của đa thức Chebyshev loại I, còn được gọi là các điểm Chebyshev (Chebyshev node), được dùng trong đa thức nội suy. Nhờ có nó, mà sai số do hiệu ứng Runge là nhỏ nhất.
Trong phương trình vi phân, đa thức Chebyshev loại I và loại II lần lượt là nghiệm của 2 phương trình vi phân Chebyshev sau:
và
-
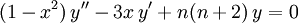 .
.
Định nghĩa[sửa]
Định nghĩa theo công thức truy hồi[sửa]
Đa thức Chebyshev loại I xác định theo công thức truy hồi:
Công thức tổng quát quy ước của Tn
Công thức mũ tổng quát
Đa thức Chebyshev loại II xác định theo công thức truy hồi:
Một công thức tổng quát của Un
Định nghĩa theo lượng giác[sửa]
Đa thức Chebyshev loại I có thể định nghĩa bằng lượng giác:
hoặc là:
với n = 0, 1, 2, 3, ....
Định nghĩa theo lượng giác của đa thức Chebyshev loại II:
công
thức
này
khá
giống
với
nhân
Dirichlet
(Dirichlet
kernel)
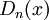 :
:
-
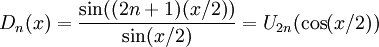 .
.
Dễ
thấy,
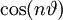 là
đa
thức
bậc
n
với
là
đa
thức
bậc
n
với
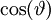 là
biến.
Đồng
thời,
là
biến.
Đồng
thời,
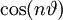 cũng
là
phần
thực
trong
công
thức
Moivre
(de
Moivre's
formula).
cũng
là
phần
thực
trong
công
thức
Moivre
(de
Moivre's
formula).
Từ công thức tổng quát bằng lượng giác ở trên, có thể dễ dàng chứng minh công thức truy hồi:
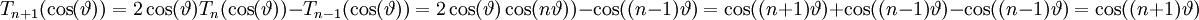
Sau đây, ta sẽ kiểm tra tính đúng đắn của định nghĩa đa thức Chebyshev theo lượng giác, với n = 0 và n = 1:
và:
và với đa thức Chebyshev bậc 2 và 3:
tương tự cho các bậc cao hơn.
Một tính chất khá thú vị của đa thức Chebyshev:
Mối liên hệ giữa đa thức Chebyshev và số phức: cho z = a + bi,
Định nghĩa theo phương trình Pell[sửa]
Trong vành R[x] (tập hợp các đa thức với hệ số thực), [1] đa thức Chebyshev được định nghĩa như nghiệm của phương trình Pell biến thể:
-
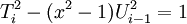 .
.
Sử dụng kĩ thuật giải phương trình Pell có tên là "nghiệm sinh từ nghiệm nhỏ nhất", suy ra công thức tổng quát sau:
Tính chất[sửa]
Công thức liên hệ (Transformation)[sửa]
Các công thức liên hệ:
-
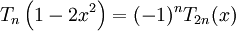 (trans.1)
(trans.1)
và
-
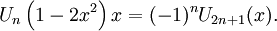 (trans.2)
(trans.2)
Chứng minh quy nạp công thức (trans.1):
Với n=0:
và n = 1:
-
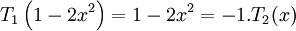 ,
,
do đó công thức (trans.1) đúng với n=0 và n=1.
Giả sử (trans.1) đúng với n > 0, ta chứng minh nó đúng với n+1:
(theo
giả
thiết
quy
nạp
ta
thay
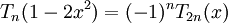 và
và
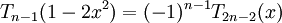 )
)
-
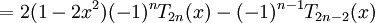
-
![=-4x^{2}(-1)^{n}T_{{2n}}(x)+(-1)^{n}.[T_{{2n}}(x)+T_{{2n-2}}(x)]+(-1)^{n}.T_{{2n}}(x)](https://tusach.thuvienkhoahoc.com/images/math/c/9/8/c98db17420ce5d11e129f602fcab59ee.png)
-
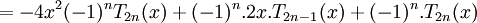
-
![=-2x(-1)^{n}[2xT_{{2n}}(x)-T_{{2n-1}}(x)]+(-1)^{n}.T_{{2n}}(x)](https://tusach.thuvienkhoahoc.com/images/math/4/3/c/43c3345f85e6e7bf5ee7da1225bf592e.png)
-
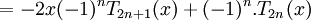
-
![=(-1)^{{n+1}}[2xT_{{2n+1}}(x)-T_{{2n}}(x)]](https://tusach.thuvienkhoahoc.com/images/math/4/f/e/4fe6f295e1a54d23104331af13472e15.png)
-
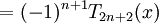 .
.
Như vậy (trans.1) đúng với n+1, theo quy tắc quy nạp, nó đúng với mọi n (điều phải chứng minh).
Chứng minh quy nạp tương tự cho (trans.2). Bản mẫu:Hidden end
Nghiệm và cực trị[sửa]
Một đa thức Cheybyshev bậc n (cả hai loại) có n nghiệm thực phân biệt, gọi là nghiệm Chebyshev, các nghiệm này đều nằm trên khoảng [−1,1]. Các nghiệm này đôi khi được gọi là các điểm nút Chebyshev (tiếng Anh: Chebyshev nodes) bởi vì chúng được dùng trong đa thức nội suy. Sử dụng định nghĩa lượng giác của đa thức Chebyshev, với
ta có thể chứng minh dễ dàng các nghiệm của Tn là
Tương tự, các nghiệm của Un là
Giá trị cực đại của đa thức Chebyshev loại I trên khoảng −1 ≤ x ≤ 1 bằng 1 và giá trị cực tiểu bằng -1. Đa thức Chebyshev chỉ có 2 giá trị tới hạn, giống như đặc tính của đa thức Shabat.
Cả 2 loại đa thức Chebyshev đều đạt cực trị tại 2 điểm đầu mút :
Đạo hàm và tích phân[sửa]
Đạo hàm[sửa]
Khi đạo hàm các đa thức Chebyshev trong dạng lượng giác, ta suy ra:
Điểm
đặc
biệt
của
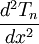 (là
giá
trị
mà
khi
thay
vào
làm
cho
nó
có
dạng
0/0
dạng
không
xác
định(indeterminate
form))
là
x
=
1
and
x=-1.
Tại
đó
(là
giá
trị
mà
khi
thay
vào
làm
cho
nó
có
dạng
0/0
dạng
không
xác
định(indeterminate
form))
là
x
=
1
and
x=-1.
Tại
đó
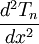 bằng:
bằng:
Đạo hàm bậc hai của đa thức Chebyshev loại I:
nếu
thay
trực
tiếp
x
=
±1
vào
thì
nó
có
dạng
không
xác
định
 .
Mặt
khác,
.
Mặt
khác,
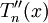 là
một
đa
thức,
do
đó
nó
có
giá
trị
thực
xác
định
tại
x
=
±1.
Và
ta
có
thể
tính
giá
trị
tại
điểm
x
=
1
bằng
giới
hạn
sau:
là
một
đa
thức,
do
đó
nó
có
giá
trị
thực
xác
định
tại
x
=
±1.
Và
ta
có
thể
tính
giá
trị
tại
điểm
x
=
1
bằng
giới
hạn
sau:
Phân tích mẫu số:
Ở
đây
mẫu
số
vẫn
bằng
0,
suy
ra
tử
số
nhất
định
bằng
0
(vì
giới
hạn
tồn
tại),
cụ
thể
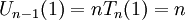 .
Đến
đây
ta
áp
dụng
quy
tắc
'Hôpital's:
.
Đến
đây
ta
áp
dụng
quy
tắc
'Hôpital's:
Chứng
minh
cho
trường
hợp
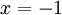 tương
tự
bằng
cách
áp
dụng
tương
tự
bằng
cách
áp
dụng
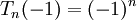 .
Bản
mẫu:Hidden
end
.
Bản
mẫu:Hidden
end
Công thức tổng quát:
Kết quả này có ý nghĩa rất lớn trong tìm đáp số của giá trị đặc trưng .
Tích phân[sửa]
Tích phân của Un:
Tích phân của Tn:
Tính trực giao[sửa]
Dãy Tn và dãy Un đều là dãy đa thức trực giao.
Cụ
thể
hơn,
các
đa
thức
loại
I,
xác
định
trên
khoảng
mở
(−1,1)với
mật
độ
(Tiếng
Anh:
The
polynomials
of
the
first
kind
are
orthogonal
with
respect
to
the
weight):
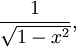 thì:
thì:
Tính
chất
trên
được
chứng
minh
bằng
cách
thay
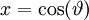 và
sử
dụng
đẳng
thức
và
sử
dụng
đẳng
thức
-
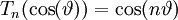 .
.
Tương
tự
các
đa
thức
loại
II
xác
định
trên
khoảng
đóng
[−1,1]
với
mật
độ
(tiếng
Anh:
The
polynomials
of
the
second
kind
are
orthogonal
with
respect
to
the
weight):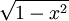
thì:
(Chú
ý
giá
trị
lượng
(weight)
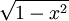 là
mật
độ
của
phân
bố
nửa
đường
tròn
Wigner
(tiếng
Anh:
Wigner
semicircle
distribution).
là
mật
độ
của
phân
bố
nửa
đường
tròn
Wigner
(tiếng
Anh:
Wigner
semicircle
distribution).
Đa thức Tn cũng thỏa mãn tính trực giao rời rạc (iếng Anh: discete orthogonality):
với
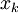 là
không
điểm
Gauss–Lobatto
thứ
N
của
là
không
điểm
Gauss–Lobatto
thứ
N
của
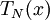
Định chuẩn nhỏ nhất[sửa]
Với số nguyên bất kì n ≥ 1, trong số các đa thức bậc n với hệ số bậc cao nhất bằng 1, đa thức sau:
có giá trị tuyệt đối lớn nhất trên đoạn [−1, 1] nhỏ nhất.
Trong
công
thức
trên
sở
dĩ
nhân
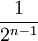 với
với
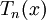 là
bởi
vì
hệ
số
bậc
cao
nhất
của
đa
thức
là
bởi
vì
hệ
số
bậc
cao
nhất
của
đa
thức
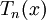 luôn
bằng
luôn
bằng
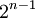 .
.
Giá trị lớn nhất đó bằng:
và |ƒ(x)| đạt giá trị lớn nhất tại n + 1 điểm:
Giả
sử
tồn
tại
đa
thức
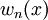 bậc
n
với
hệ
số
bậc
cao
nhất
bằng
1,
và
giá
trị
tuyệt
đối
lớn
nhất
trên
[−1, 1]
nhỏ
hơn
bậc
n
với
hệ
số
bậc
cao
nhất
bằng
1,
và
giá
trị
tuyệt
đối
lớn
nhất
trên
[−1, 1]
nhỏ
hơn
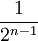 .
.
Xét đa thức sau:
đa thức này có bậc nhỏ thua n.
Do
giả
thiết,
tại
mỗi
điểm
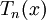 bằng
bằng
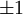 ,
thì
,
thì
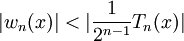
-
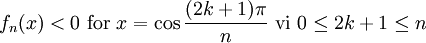 .
.
Như
vậy
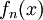 có
nghiệm
trên
n
khoảng
có
nghiệm
trên
n
khoảng
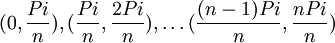 .
Nói
cách
khác,
nó
có
ít
nhất
n
nghiệm,
điều
này
vô
lí
vì
.
Nói
cách
khác,
nó
có
ít
nhất
n
nghiệm,
điều
này
vô
lí
vì
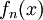 là
đa
thức
bậc
≤(n-1).
là
đa
thức
bậc
≤(n-1).
Suy ra điều giả sử là sai. ta có điều phải chứng minh. Bản mẫu:Hidden end
Mối liên hệ với các loại đa thức khác[sửa]
Đa thức Chebyshev là trường hợp đặc biệt của Jacobi and đa thức Gegenbauer,
Các tính chất khác[sửa]
Đa thức Chebyshev là trường hợp đặc biệt của đa thức Gegenbauer, đến lượt mình đa thức Gegenbauer lại là trường hợp đặc biệt của Jacobi.
Với số nguyên n bất kì, Tn(x) và Un(x) đều là đa thức bậc n.
Nếu n chẵn thì Tn(x) và Un(x) là hàm chẵn, nghĩa là chỉ có các hệ số tương ứng với bậc chẵn là khác 0.
Ví dụ:
-
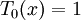
-
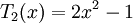
-
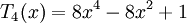 .
.
-
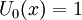
-
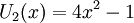
-
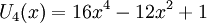 .
.
Nếu
n
lẻ
thì
Tn(x)
và
Un(x)
là
hàm
lẻ,
nghĩa
là
chỉ
có
các
hệ
số
tương
ứng
với
bậc
lẻ
là
khác
0.
Ví dụ:
-
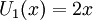
-
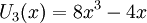 .
.
Hệ số bậc cao nhất của Tn là 2n − 1 if 1 ≤ n, và 1 tương ứng với bậc bằng 0.
Tn là trường hợp riêng của đường cong Lissajous curve với tần số tỉ lệ (tiếng Anh: frequency ratio) là n.
Một số dãy đa thức khác, ví dụ đa thức Lucas (Ln), đa thức Dickson(Dn), và đa thức Fibonacci(Fn) có liên hệ với đa thức Chebyshev Tn and Un.
Đa thức Chebyshev loại I thỏa mãn công thức truy hồi sau:
với mọi j và k.
Đối với đa thức Chebyshev loại II là:
-
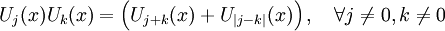 .
.
Từ
công
thức:
suy ra công thức sau:
-
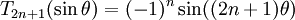 .
.
Ví dụ[sửa]
Các đa thức Chebyshev loại I đầu tiên:
Các đa thức Chebyshev loại II đầu tiên:
Xem thêm[sửa]
- Điểm Chebyshev
- Bộ lọc Chebyshev
- Căn bậc ba Chebyshev
- Đa thức Dickson
- Đa thức Legendre
- Đa thức Hermite
- Hàm hữu tỉ Chebyshev
- Cầu phương Clenshaw–Curtis
- Lý thuyết xấp xỉ
Ghi chú[sửa]
Lỗi
chú
thích:
Tồn
tại
thẻ
<ref>,
nhưng
không
tìm
thấy
thẻ
<references/>