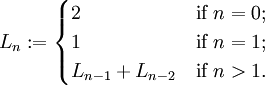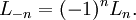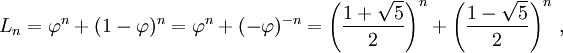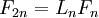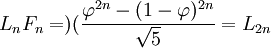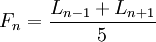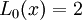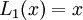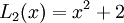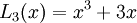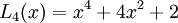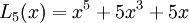Số Lucas
Số Lucas là một dãy số được đặt tên nhằm vinh danh nhà toán học François Édouard Anatole Lucas (1842–1891), người đã nghiên cứu dãy số Fibonacci, dãy số Lucas và các dãy tương tự. Giống như dãy Fibonacci, mỗi số trong dãy Lucas bằng tổng của hai số liền trước nó. Dãy số gồm thương giữa hai số Lucas liền nhau sẽ hội tụ đến giới hạn bằng tỉ lệ vàng.
Tuy vậy khác với dãy Fibonacci, hai số đầu tiên trong dãy Lucas là L0 = 2 và L1 = 1 (trong dãy Fibonacci là 0 và 1). Chính vì thế mà một số tính chất của số Lucas sẽ khác với số Fibonacci.
Công thức truy hồi của dãy:
Các số đầu tiên của dãy Lucas:
Mục lục
Số Lucas có chỉ số âm[sửa]
Sử
dụng
công
thức
truy
hồi
ngược
lại
Ln-2
=
Ln
-
Ln-1
để
mở
rộng
số
Lucas
tới
các
số
nguyên
âm.
Ta
có
thể
thêm
các
giá
trị
sau
vào
đãy
Lucas
(với
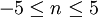 ):
(...
-11,
7,
-4,
3,
-1,
2,
1,
3,
4,
7,
11,
...)
.
):
(...
-11,
7,
-4,
3,
-1,
2,
1,
3,
4,
7,
11,
...)
.
Các số Lucas âm có tính chất (chứng minh bằng quy nạp):
Tính chất[sửa]
Công thức tổng quát[sửa]
Công thức tổng quát của số Lucas:
với
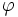 bằng
Tỉ
lệ
vàng.
bằng
Tỉ
lệ
vàng.
Một
tính
chất
khá
thú
vị,
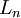 là
số
nguyên
gần
với
là
số
nguyên
gần
với
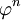 nhất.
nhất.
Mối liên hệ với các số Fibonacci[sửa]
Số Lucas liên hệ với số Fibonacci bởi các hằng đẳng thức sau:
-
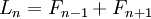
- tổng quát hơn là công thức sau:
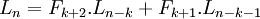 với
mọi
k<n;
(2.1)
Bản
mẫu:Hidden
begin
với
mọi
k<n;
(2.1)
Bản
mẫu:Hidden
begin
Chứng minh quy nạp.
k=0, thì công thức (2.1) hiển nhiên đúng.
Giả sử (2.1) đúng đến k<n-1, ta chứng minh nó đúng với k+1, thật vậy:
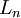
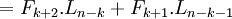
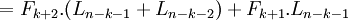
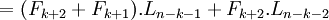
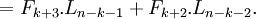
Vậy là (2.1) cũng đúng với k+1.
Suy ra điều phải chứng minh.
-
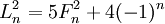 ,
từ
hệ
thức
liên
hệ
này
suy
ra
tỉ
số
,
từ
hệ
thức
liên
hệ
này
suy
ra
tỉ
số
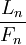 tiến
đến
tiến
đến
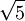 khi
khi
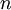 tiến
đến
+∞.
tiến
đến
+∞.
Bản mẫu:Hidden begin Sử dụng công thức tổng quát. Bản mẫu:Hidden end
Bản mẫu:Hidden begin Chứng minh, sử dụng công thức tổng quát:
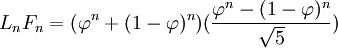
Rút gọn lại được:
Bản mẫu:Hidden begin Chứng minh bằng quy nạp theo n. Bản mẫu:Hidden end
Khi chỉ số là số nguyên tố[sửa]
Ln đồng dư với 1 mod n nếu n là số nguyên tố. Ngoài ra, Ln cũng có tính chất này với một số giá trị khác của n.
Tính chia hết giữa các số Lucas[sửa]
Lmn chia hết cho Ln nếu m là số lẻ. Điều đó dẫn đến điều kiện cần của n để Ln là số nguyên tố.
Bản
mẫu:Hidden
begin
Sử
dụng
công
thức
tổng
quát
của
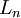 ,
để
chứng
minh
hệ
thức
truy
hồi
sau:
,
để
chứng
minh
hệ
thức
truy
hồi
sau:
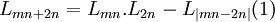
Từ đó suy ra:
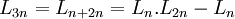
Suy
ra
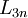 chia
hết
cho
chia
hết
cho
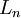 .
.
Lại
dùng
công
thức
truy
hồi
(1),
suy
ra
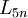 chia
hết
cho
chia
hết
cho
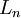 .
.
Lặp
lại
thao
tác
trên
k
lần
liên
tiếp,
suy
ra
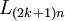 chia
hết
cho
chia
hết
cho
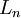 ,
điều
phải
chứng
minh.
,
điều
phải
chứng
minh.
Số nguyên tố Lucas[sửa]
Số nguyên tố Lucas là số Lucas, và đồng thời là một nguyên tố. Các số nguyên tố Lucas nhỏ nhất được biết là:
- 2, 3, 7, 11, 29, 47, 199, 521, 2207, 3571, 9349, ... Bản mẫu:OEIS
Nếu Ln là số nguyên tố thì n bằng 0, nguyên tố, hoặc là lũy thừa của 2.[1]
Các
số
Lucas
có
dạng
L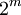 là
số
nguyên
tố
được
biết
cho
đến
nay
là
là
số
nguyên
tố
được
biết
cho
đến
nay
là
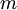 =
1,
2,3
và
4.
=
1,
2,3
và
4.
Đa thức Lucas[sửa]
Các đa thức Lucas được xác định mô phỏng theo dãy số Lucas. Dãy đa thức này được xây dựng bằng công thức truy hồi như sau:
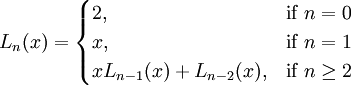
Sau đây là công thức dạng tường minh của các đa thức Lucas đầu tiên:
Xem thêm[sửa]
Chú thích[sửa]
Lỗi
chú
thích:
Tồn
tại
thẻ
<ref>,
nhưng
không
tìm
thấy
thẻ
<references/>