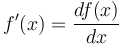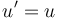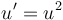Phương trình vi phân

Phương trình vi phân hay phương trình sai phân là một phương trình toán học nhằm biểu diễn mối quan hệ giữa một hàm chưa được biết (một hoặc nhiều biến) với đạo hàm của nó (có bậc khác nhau). Phương trình sai phân đóng vai trò cực kì quan trọng trong kĩ thuật, vật lí, kinh tế và một số ngành khác. Ví dụ: một phương trình sai phân đơn giản

$f'(x)={\frac {df(x)}{dx}}\,$

Chú ý trong phương trình ví dụ trên, nếu f(x) biểu diễn cho vận tốc của một vật thì f'(x) chính là gia tốc của vật đó (là đại lượng đặc trưng cho độ biến thiên vận tốc). Sự ra đời của phương trình sai phân cũng xuất phát từ việc xác định mối quan hệ xác định giữa một bên là một đại lượng biến thiên liên tục (được biểu diễn bằng hàm f(x)) và bên còn lại là độ biến thiên của đại lượng đó (biểu diễn bằng đạo hàm bậc 1 hoặc cao hơn). Điều này được thể hiện rõ trong cơ học cổ điển. Cụ thể là Định luật Newton về chuyển động cho phép xác định ví trí của một vật dựa vào vận tốc, gia tốc, và một số lực tác động được biểu diễn dưới dạng hàm sai phân theo thời gian.

Tập tin:Airflow-Obstructed-Duct.png

Minh hoạ dòng không khí chảy vào ống dẫn được mô hình dùng các phương trình Navier-Stokes, một tập các phương trình sai phân riêng phần.

Đối với các hàm thông thường, nghiệm là một giá trị số (thực, phức...). Còn trong phương trình sai phân, mục tiêu là tìm ra công thức của hàm chưa được biết nhằm thỏa mãn mối quan hệ đề ra. Thông thường, nó sẽ là một họ các phương trình, sai lệch bằng một hằng số C nào đó. Hàm này sẽ được xác định chính xác khi có thêm điều kiện ban đầu hoặc điều kiện biên.

Trong các ứng dụng thực tế, việc tìm ra công thức của hàm đôi lúc nhiều lúc khó khăn. Thực tiễn người ta cũng chỉ quan tâm tới giá trị của hàm tại các giá trị cụ thể của các biến độc lập. Các phương pháp nhằm tìm ra giá trị chính xác của hàm được gọi là phân tích định lượng (quantitative analysis). Tuy nhiên, có những ứng dụng mà ngay cả giá trị thực cũng khó tìm ra, lúc này người ta lại quan tâm đến giá trị xấp xỉ (có một độ chính xác nhất định) với giá trị thực. Việc giải các giá trị này thường được thực hiện bằng các phương pháp số (numerical methods) và công cụ là máy tính. Các phương pháp cho cách sau gọi là phân tích số (numerical analysis)

Hướng nghiên cứu

Phương trình sai phân được nghiên cứu rộng rãi trong toán học thuần túy và ứng dụng, vật lí, và các ngành kĩ thuật.

• Toán học thuần túy thì quan tâm đến việc tìm ra sự tồn tai và duy nhất của hàm nghiệm
• Toán học ứng dụng thì tập trung vào các phương pháp để xấp xỉ hàm nghiệm
• Một số ngành khác thì dùng phương trình sai phân trong mô hình các quá trình vật lí, sinh học và kĩ thuật. Ví dụ: tương tác giữa các nguyên tử trong phân tử, hay giữa các neuron thần kinh. Khi áp dụng trong các ứng dụng thực tiễn, thì việc tìm ra dạng đóng của hàm nghiệm là không cần thiết. Thay vào đó, chúng có thể được xấp xỉ bằng các phương pháp số.
• Các nhà toán học cũng nghiên cứu nghiệm yếu (weak solution) (dựa vào đạo hàm yếu (weak derivative)).
• Việc nghiên cứu tính ổn định của hàm nghiệm của các phương trình sai phân là thuộc về lý thuyết ổn định (stability theory).

Các loại phương trình sai phân

• Phương trình vi phân thường (ODE) là phương trình vi phân trong đó hàm chưa biết là hàm 1 biến độc lập.
• Phương trình vi phân riêng phần (PDE) là phương trình vi phân trong đó hàm chưa biết là hàm của nhiều biến độc lập và các đạo hàm riêng của nó.
• delay differential equation (DDE) là phương trình vi phân trong đó giá trị đạo hàm của hàm chưa biết tại một thời điểm nào đó là tính theo giá trị của hàm tại một thời điểm khác.
• stochastic differential equation (SDE) là phương trình vi phân trong đó một hoặc vài số hạng là quá trình ngẫu nhiên, vì thế dẫn đến hàm nghiệm cũng là một quá trình ngẫu nhiên (stochastic process).
• differential algebraic equation (DAE) là phương trình sai phân trong đó có chứa các số hạng là đại số và sai phân.

Mỗi loại trên lại chia thành tuyến tính và phi tuyến tính. Một phương trình sai phân là tuyến tính nếu mọi đạo hàm của nó đều tính theo hàm có dạng mũ 1 và không có tích hay hàm của các biến phụ thuộc. Ngược lại, thì là hàm phi tuyến.Ví dụ nếu u′ là đạo hàm bậc nhất của u, thì phương trình

$u'=u\,$

là tuyến tính, trong khi phương trình

$u'=u^{2}\,$

là phi tuyến. Việc giải các phương trình sai phân tuyến tính có thể thực hiện được nhưng đối với phương trình sai phân phi tuyến, không có công thức chung để giải, ngoại trừ chúng có tính đối xứng.; xem đối xứng và bất biến. Thay vào đó, họ thường dùng hàm tuyến tính để xấp xỉ hàm phi tuyến, với những điều kiện ràng buộc nhất định.

Một khái niệm hay nói đến là bậc của hàm, đó chính là bậc của đạo hàm cao nhất (của một biến phụ thuộc) xuất hiện trong hàm sai phân.

Các phương trình vi phân nổi tiếng

• Định luật 2 Newton trong động lực học
• Phương trình Hamilton trong cơ học cổ điển
• Phân rã phóng xạ (Radioactive decay) trong vật lí hạt nhân
• Định luật làm lạnh Newton trong nhiệt động lực học
• Phương trình sóng
• Phương trình Maxwell trong trường điện từ
• Phương trình nhiệt trong nhiệt động lực học
• Phương trình Laplace
• Phương trình Poisson
• Phương trình trường Einstein trong thuyết tương đối rộng
• Phương trình Schrödinger trong cơ học lượng tử
• geodesic equation
• Phương trình Navier-Stokes trong động học chất lỏng
• Phương trình Lotka-Volterra trong population dynamics
• Phương trình Black-Scholes trong tài chính
• Phương trình Cauchy-Riemann trong giải tích phức
• shallow water equations

Xem thêm

• Định lí Picard-Lindelöf về sự tồn tại và tính duy nhất của hàm nghiệm
• Hàm tích phân
• Hàm sai phân phức

Tham khảo

• D. Zwillinger, Handbook of Differential Equations (3rd edition), Academic Press, Boston, 1997.
• A. D. Polyanin and V. F. Zaitsev, Handbook of Exact Solutions for Ordinary Differential Equations (2nd edition), Chapman & Hall/CRC Press, Boca Raton, 2003. ISBN 1-58488-297-2.
• W. Johnson, A Treatise on Ordinary and Partial Differential Equations, John Wiley and Sons, 1913, in University of Michigan Historical Math Collection
• E.L. Ince, Ordinary Differential Equations, Dover Publications, 1956
• E.A. Coddington and N. Levinson, Theory of Ordinary Differential Equations, McGraw-Hill, 1955
• P. Blanchard, R.L. Devaney, G.R. Hall, Differential Equations, Thompson, 2006

Liên kết ngoài

• Bài giảng về phương trình sai phân MIT Open CourseWare video
• Online Notes / Differential Equations Paul Dawkins, Lamar University
• Differential Equations, S.O.S. Mathematics
• Introduction to modeling via differential equations Introduction to modeling by means of differential equations, with critical remarks.
• Differential Equation Solver Java applet tool used to solve differential equations.
• Mathematical Assistant on Web online solving first order (linear and with separated variables) and second order linear differential equations (with constant coefficients), including intermediate steps in the solution, powered by Maxima
• Exact Solutions of Ordinary Differential Equations
• A bibliography of books about differential equations, from the Mathematical Association of America
• Collection of ODE and DAE models of physical systems MATLAB models
• ODE Examples with Solutions

Bản mẫu:Toán

Liên kết đến đây

• Đa thức Chebyshev
• Bức xạ điện từ
• James Clerk Maxwell
• Leonhard Euler
• Lực
• Phương trình
• Đại số tuyến tính
• Toán học
• Vật lý học