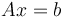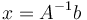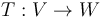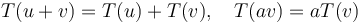Đại số tuyến tính

Từ VLOS
Bước tới: chuyển hướng, tìm kiếm

Đại số tuyến tính là một ngành toán học nghiên cứu về không gian vectơ, hệ phương trình tuyến tính và các phép biến đổi tuyến tính giữa chúng.

Các khái niệm vectơ trong không gian vectơ, ma trận và các định thức là những công cụ rất quan trọng trong đại số tuyến tính. Bài toán cơ bản của đại số tuyến tính là tìm nghiệm x của phương trình ma trận sau:

Ax=b

Mặc dù nghiệm này về lý thuyết có thể tìm được từ ma trận nghịch đảo:

x=A^{{-1}}b

nhưng các phương pháp số ví dụ như phép khử Gauss thường hiệu quả hơn.

Đại số tuyến tính được sử dụng nhiều trong toán học, như trong đại số đại cương, giải tích hàm, hình học giải tích... để giải các bài toán như phép quay trong không gian, nội suy bình phương nhỏ nhất, nghiệm của hệ phương trình vi phân, tìm đường tròn qua ba điểm... Nó cũng có vô vàn ứng dụng trong khoa học tự nhiên (vật lý, công nghệ...) và khoa học xã hội (kinh tế...), vì các mô hình phi tuyến tính hay gặp trong tự nhiên và xã hội thường có thể xấp xỉ bằng mô hình tuyến tính.

Phạm vi nghiên cứu[sửa]

Không gian vector[sửa]

Cấu trúc chính của đại số tuyến tính là các không gian vector. Một không gian vector trên trường số F là một tập V kèm theo phép toán hai ngôi. Các phần tử trong V gọi là những vector, các phần tử trong F gọi là vô hướng. Phép toán đầu tiên là phép cộng vector, cộng 2 vector v và w cho ra một vector thứ 3 v + w. Phép toán thứ hai là phép nhân một vô hướng a với bất kỳ vector v nào và kết quả cho ra một vector mới av, phép toán này gọi là phép nhân vô hướng của v với a. Các phép nhân và cộng trong không gian vector phải thỏa mãn các tiên đề sau,[1] với u, v và w là các vector trong tập V, a và b là các vô hướng trong trường số F.

Tiên đề Công thức biểu diễn
Tính kết hợp của phép cộng u + (v + w) = (u + v) + w
Tính giao hoán của phép cộng u + v = v + u
Phần tử trung hòa của phép cộng Tồn tại một phần tử 0 ∈ V, sao cho v + 0 = v với mọi v ∈ V.
Phần tử nghịch đảo của phép cộng Với mọi v ∈ V, tồn tại một phần tử −v ∈ V, gọi là phần tử nghịch đảo của v, sao cho v + (−v) = 0
Tính phân phối của một phép nhân vô hướng với một phép cộng vector   a(u + v) = au + av
Tính phân phối của một phép nhân vô hướng với một phép cộng vô hướng (a + b)v = av + bv
Phép nhân vô hướng kết hợp với phép nhân trong trường các số vô hướng a(bv) = (ab)v [nb 1]
Phần tử đơn vị trong phép nhân vô hướng 1v = v, với 1 là phần tử đơn vị của phép nhân trong trường số F.

Ánh xạ tuyến tính[sửa]

Cho 2 không gian vector V và W trên trường F, một biến đổi tuyến tính (còn gọi là ánh xạ tuyến tính) là một ánh xạ:

T:V\to W

có tính kết hợp với phép cộng và phép nhân vô hướng:

T(u+v)=T(u)+T(v),\quad T(av)=aT(v)

với mọi vector u,v ∈ V và một vô hướng a ∈ F.

Các chủ đề chính[sửa]

Lịch sử[sửa]

Lịch sử đại số tuyến tính bắt đầu từ năm 1843 và 1844. Năm 1843, William Rowan Hamilton (người đã nghĩ ra chữ vector) khám phá ra quaternion. Năm 1844, Hermann Grassmann xuất bản quyển Die lineare Ausdehnungslehre (xem mục tham khảo).

Giới thiệu chung[sửa]

Trong trường đại học, đại số tuyến tính bắt đầu từ nghiên cứu các vector trong hệ tọa độ Đề-các 2 chiều hoặc 3 chiều. Các vectơ là các đoạn thẳng có hướng và độ lớn. Các kết quả trong không gian 2 hoặc 3 chiều có thể được mở rộng ra cho nhiều chiều hơn, gọi tổng quát là không gian vectơ.

Không gian vectơ là một khái niệm trừu tượng của đại số trừu tượng, được định nghĩa trên một trường toán học, phổ biến trong ứng dụng là trường số thực hoặc trường số phức.

Các biến đổi tuyến tính chuyển các phần tử trong một không gian vectơ này sang không gian vectơ kia, tuân thủ phép cộng và phép nhân vô hướng. bản thân tập hợp của các biến đổi này cũng hình thành nên không gian vectơ của chính chúng.

Nếu hệ cơ sở của một không gian vectơ là cố định, mọi biến đổi tuyến tính đều có thể viết thành bảng gọi là ma trận. Việc nghiên cứu các tính chất của ma trận, như định thức và vectơ riêng là một phần quan trọng của đại số tuyến tính.

Sử dụng đại số tuyến tính có thể giải chính xác hoặc gần đúng rất nhiều bài toán, bao gồm cả các bài toán không tuyến tính. Lý do là ta luôn có thể sử dụng vi giải tích để biến các hàm không tuyến tính thành gần đúng tuyến tính ở gần những điểm quan tâm. Phương pháp này là một trong những phương pháp phổ biến nhất trong toán học ứng dụng vào khoa học và kỹ thuật.

Một số định lý quan trọng[sửa]

  1. A là khả nghịch
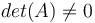  2. det(A)\neq 0.
  3. rank(A)=n.
  4. null(A)=0.
  5. A không có trị riêng bằng 0.
  6. Với mọi b, Ax=b có duy nhất một nghiệm x.
  7. ATA là khả nghịch.
  8. Các hàng (hoặc cột) của A tạo nên các vector độc lập tuyến tính trong không gian vector của A.

Chú thích[sửa]

  1. ↑

Ghi chú[sửa]

  1. ↑ Tiên đề này không khẳng định về tính kết hợp của một toán tử, bởi vì có hai toán tử đang nói đến, nhân vô hướng: bv; và nhân trên trường số: ab.

Xem thêm[sửa]

Tham khảo[sửa]

  • Grassmann, Hermann, Die lineare Ausdehnungslehre dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie, 1844.

Liên kết đến đây

Lấy từ “https://tusach.thuvienkhoahoc.com/index.php?title=Đại_số_tuyến_tính&oldid=112327”