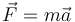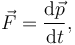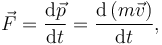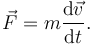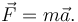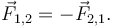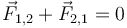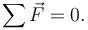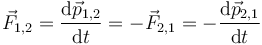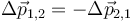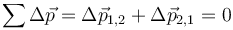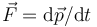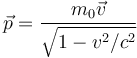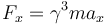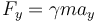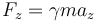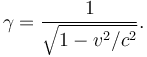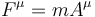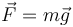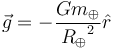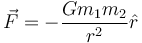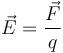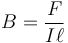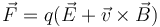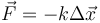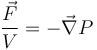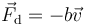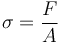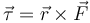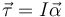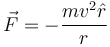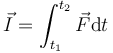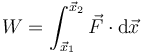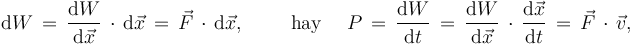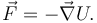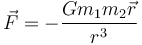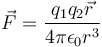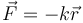Lực
Bản mẫu:Infobox Physical quantity
Trong vật lý học, lực là bất kỳ ảnh hưởng nào làm một vật thể chịu sự thay đổi, hoặc là ảnh hưởng đến chuyển động, hướng của nó hay cấu trúc hình học của nó. Nói cách khác, lực là nguyên nhân làm cho một vật có khối lượng thay đổi vận tốc của nó (bao gồm chuyển động từ trạng thái nghỉ), tới chuyển động có gia tốc, hay làm biến dạng vật thể, hoặc cả hai. Lực cũng có thể được miêu tả bằng những khái niệm trực giác như sự đẩy hoặc kéo. Lực là đại lượng vectơ có độ lớn và hướng. Trong hệ đo lường SI nó có đơn vị là newton và ký hiệu là F.
Định luật thứ hai của Newton ở dạng ban đầu phát biểu rằng tổng lực tác dụng lên một vật bằng với tốc độ thay đổi của động lượng theo thời gian.[1]Bản mẫu:Rp Nếu khối lượng của vật không đổi, định luật này hàm ý rằng gia tốc của vật tỷ lệ thuận với tổng lực tác dụng lên nó, cũng như theo hướng của tổng lực, và tỷ lệ nghịch với khối lượng của vật. Biểu diễn bằng công thức:
với mũi tên ám chỉ đây là đại lượng vectơ có độ lớn và hướng.
Những khái niệm liên quan đến lực gồm: phản lực, làm tăng vận tốc của vật; lực cản làm giảm vận tốc của vật; và mô men lực tạo ra sự thay đổi trong vận tốc quay của vật. Nếu không coi vật là chất điể,, mỗi phần của vật sẽ tác dụng những lực lên những phần bên cạnh nó; sự phân bố những lực này trong vật thể được gọi là ứng suất cơ học.[2] Áp suất là một dạng đơn giản của ứng suất. Ứng suất thường làm biến dạng vật rắn hoặc tạo ra dòng trong chất lưu.[1][3]Bản mẫu:Rp[4]
Mục lục
Sự hình thành khái niệm[sửa]
Các nhà triết học thời cổ điển đã sử dụng khái niệm lực trong nghiên cứu những vật chuyển động và đứng yên cũng như các máy đơn giản, tuy thế các triết gia như Aristotle và Archimedes đã mắc phải những sai sót cơ bản khi nghiên cứu về lực. Một phần là do sự hiểu biết không đầy đủ về biểu hiện lực của ma sát, dẫn đến cách nhìn không thỏa đáng về bản chất của chuyển động trong tự nhiên.[5] Một sai lầm cơ bản đó là niềm tin rằng lực là cần thiết để duy trì sự chuyển động, ngay cả với vận tốc không đổi. Hầu hết những hiểu lầm trước đó về chuyển động và lực cuối cùng đã được Isaac Newton miêu tả đúng đắn; với ý nghĩa toán học bên trong, ông đã thiết lập lên các định luật về chuyển động mà đã đứng vững trong gần ba trăm năm.[4] Đầu thế kỷ 20, Albert Einstein phát minh ra thuyết tương đối cho phép tiên đoán đúng đắn tác dụng của lực lên những vật với chuyển động xấp xỉ tốc độ ánh sáng, cũng như mang lại hiểu biết mới về bản chất của lực hấp dẫn và quán tính.
Cùng với tầm nhìn hiện đại theo cơ học lượng tử và công nghệ cho phép gia tốc các hạt cơ bản tới gần tốc độ ánh sáng, vật lý hạt đã đưa ra Mô hình chuẩn để miêu tả các lực giữa những hạt hạ nguyên tử. Mô hình chuẩn tiên đoán sự trao đổi các hạt gọi là boson gauge (boson chuẩn) có ý nghĩa như các lực là hấp thụ hay phát ra hạt. Chỉ có bốn tương tác cơ bản gồm: tương tác mạnh, tương tác điện từ, tương tác yếu, và tương tác hấp dẫn.[1]Bản mẫu:Rp[3]Bản mẫu:Rp Thực nghiệm của vật lý năng lượng cao trong thập niên 1970 và 1980 xác nhận rằng tương tác yếu và tương tác điện từ được thống nhất bởi tương tác điện yếu.[6]
Cơ học Newton[sửa]
- Xem chi tiết: Các định luật chuyển động của Newton
Isaac Newton miêu tả chuyển động của mọi vật bằng sử dụng khái niệm quán tính và lực, và ông cũng nhận thấy rằng chúng tuân theo một số định luật bảo toàn. Năm 1687, Newton công bố cuốn sách Philosophiæ Naturalis Principia Mathematica chứa nội dung về các nghiên cứu của ông.[4][7] Trong cuốn sách này, Newton dẫn ra ba định luật chuyển động mà cho tới ngày nay là cách mà lực được miêu tả trong vật lý học.[7]
Định luật thứ nhất[sửa]
- Xem chi tiết: Định luật thứ nhất của Newton
Định luật thứ nhất của Newton phát biểu rằng mọi vật sẽ tiếp tục chuyển động trong trạng thái với vận tốc không đổi trừ khi nó bị tác động bởi tổng hợp lực bên ngoài.[7] Định luật này mở rộng quan niệm của Galileo về vận tốc không đổi luôn kết hợp với sự thiếu đi lực tác dụng (xem miêu tả chi tiết bên dưới). Newton đề xuất rằng mỗi vật có khối lượng sẽ có quán tính tự thân như là hàm của "trạng thái tự nhiên" cân bằng cơ bản trong ý tưởng của Aristote về "trạng thái nghỉ tự nhiên". Do vậy, định luật thứ nhất mâu thuẫn với niềm tin trực giác của Aristote rằng hợp lực là cần thiết nhằm duy trì một vật chuyển động với vận tốc không đổi. Bằng cách đặt trạng thái nghỉ không thể phân biệt về mặt vật lý với trạng thái của vật với vận tốc không đổi khác 0, định luật thứ nhất của Newton liên hệ trực tiếp quán tính với khái niệm vận tốc tương đối của Galileo. Đặc biệt, trong hệ mà các vật đang chuyển động với nhiều vận tốc khác nhau, sẽ không thể xác định được vật nào là "đang chuyển động" và vật nào là "đang đứng yên". Nói cách khác, các định luật vật lý là như nhau trong mỗi hệ quy chiếu quán tính, tức là các hệ tuân theo phép biến đổi Galileo.
Ví dụ, khi ngồi trong một chiếc xe chuyển động với vận tốc đều, các định luật vật lý xảy ra trong chiếc xe sẽ không khác gì khi nó đứng yên tương đối. Một người ngồi trong xe ném lên một quả bóng sẽ bắt lại được khi nó rơi xuống mà không bị ảnh hưởng bởi hướng và vận tốc của chiếc xe. Điều này còn đúng ngay cả khi có một người đứng ở mặt đất quan sát thấy xe chạy qua và quả bóng ném trong xe đi theo quỹ đạo parabol theo hướng của chiếc xe. Quán tính của quả bóng kết hợp với vận tốc không đổi của nó theo hướng của chiếc xe chuyển động đảm bảo rằng quả bóng tiếp tục di chuyển theo hướng đó ngay cả khi nó bị ném lên và rơi xuống. Từ quan sát của người ngồi trong xe, chiếc xe và mọi thứ khác bên trong nó ở trong trạng thái nghỉ: trong khi thế giới bên ngoài đang chuyển động với vận tốc không đổi theo hướng ngược lại với chiều chuyển động của chiếc xe. Do không có một thí nghiệm nào có thể phân biệt được chiếc xe đang đứng yên hay thế giới bên ngoài đang đứng yên, hai tình huống này được coi là không thể phân biệt được về mặt vật lý. Do đó quán tính áp dụng một cách bằng nhau cho hệ chuyển động với vận tốc đều hay khi nó đứng yên.
Có thể tổng quát khái niệm quán tính một cách sâu hơn nhằm giải thích cho xu hướng của các vật tiếp tục trong nhiều dạng khác nhau của chuyển động đều, ngay cả khi không giới hạn trong chuyển động đều. Quán tinh quay của Trái Đất thể hiện ở sự không thay đổi độ dài của ngày và của năm (khi không kể đến các ảnh hưởng khác). Albert Einstein đã mở rộng nguyên lý quán tính khi ông áp dụng cho những hệ chuyển động với gia tốc không đổi, như hệ quy chiếu gắn với các vật rơi tự do trong trường hấp dẫn Trái Đất sẽ tương đương vật lý với hệ quy chiếu quán tính. Điều này giải thích tại sao, ví dụ, các nhà du hành vũ trụ có cảm giác không trọng lượng khi ở trên quỹ đạo rơi tự do quanh Trái Đất, và tại sao các định luật chuyển động của Newton có thể dễ dàng kiểm chứng trong môi trường không trọng lực (hoặc vi trọng lực). Nếu nhà du hành đặt một vật khối lượng trong tàu vũ trụ, nó sẽ giữ trạng thái đứng im so với con tàu do quán tính. Điều này xảy ra hệt khi nhà du hành và con tàu vũ trụ ở trong không gian liên thiên hà khi không có lực tác dụng của lực hấp dẫn tác dụng lên hệ quy chiếu trong con tàu. Đây chính là nguyên lý tương đương và nó là một trong những cơ sở của thuyết tương đối tổng quát.[8]
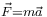 ,
mặc
dù
ông
viết
dạng
phương
trình
của
định
luật
chuyển
động
thứ
hai
khi
không
sử
dụng
phép
tính
vi
phân.
,
mặc
dù
ông
viết
dạng
phương
trình
của
định
luật
chuyển
động
thứ
hai
khi
không
sử
dụng
phép
tính
vi
phân.Định luật thứ hai[sửa]
- Xem chi tiết: Định luật thứ hai của Newton
Cách trình bày hiện đại của định luật hai Newton là dưới dạng phương trình vi phân vectơ:[Note 1]
với
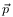 là
động
lượng
của
hệ,
và
là
động
lượng
của
hệ,
và
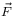 là
hợp
lực
(tổng
vectơ).
Trong
hệ
cân
bằng,
hợp
lực
tác
dụng
bằng
0,
nhưng
có
thể
có
nhiều
lực
tác
dụng
(cân
bằng
nhau)
vào
hệ.
Ngược
lại,
định
luật
thứ
hai
nói
rằng
khi
lực
không
cân
bằng
tác
dụng
lên
vật
sẽ
làm
cho
động
lượng
của
vật
thay
đổi
theo
thời
gian.[7]
là
hợp
lực
(tổng
vectơ).
Trong
hệ
cân
bằng,
hợp
lực
tác
dụng
bằng
0,
nhưng
có
thể
có
nhiều
lực
tác
dụng
(cân
bằng
nhau)
vào
hệ.
Ngược
lại,
định
luật
thứ
hai
nói
rằng
khi
lực
không
cân
bằng
tác
dụng
lên
vật
sẽ
làm
cho
động
lượng
của
vật
thay
đổi
theo
thời
gian.[7]
Theo định nghĩa của động lượng,
với
m
là
khối
lượng
và
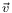 là
vận
tốc
của
nó.[1]Bản
mẫu:Rp
là
vận
tốc
của
nó.[1]Bản
mẫu:Rp
Định luật hai chỉ áp dụng cho hệ có khối lượng không đổi,[Note 2] và ở đây m có thể đưa ra ngoài toán tử đạo hàm. Phương trình lúc này trở thành
Bằng cách thay định nghĩa của gia tốc, dạng đại số của định luật hai Newton trở thành:
Định luật hai Newton chứng tỏ mối liên hệ trực tiếp của gia tốc tỷ lệ thuận với lực và khối lượng tỷ lệ nghịch với nó. Gia tốc có thể đo được thông qua định nghĩa về mặt động học. Tuy nhiên, trong khi chuyển động học được miêu tả rõ ràng thông qua phân tích hệ quy chiếu trong vật lý cao cấp, vẫn còn có những câu hỏi sâu sắc về định nghĩa bản chất của khối lượng. Thuyết tương đối rộng đề xuất sự liên hệ giữa không thời gian, trường hấp dẫn và khối lượng, nhưng hiện vẫn chưa có một lý thuyết hấp dẫn lượng tử được chấp thuận, do vậy sự liên hệ này có còn đúng khi các nhà vật lý xét ở cấp độ vi mô hay không. Với một vài điều chỉnh, định luật hai Newton có thể dùng làm định nghĩa cho phép đo về khối lượng bằng cách viết định luật dưới dạng biểu thức toán học tương đương.
Cách sử dụng định luật hai Newton làm định nghĩa cho lực không được sự đồng thuận rộng rãi trong nhiều cuốn sách vật lý nâng cao,[1]Bản mẫu:Rp[3]Bản mẫu:Rp[9] mặc dù nó đúng về bản chất toán học. Nhiều nhà vật lý, triết học và toán học nổi tiếng đi tìm một cách định nghĩa hiển cho khái niệm lực bao gồm Ernst Mach, hay Walter Noll.[10][11]
Định luật hai cũng được áp dụng để đo độ lớn của lực. Ví dụ, khi biết khối lượng của hành tinh cùng với gia tốc của nó trên quỹ đạo cho phép tính ra được lực hấp dẫn tác động lên hành tinh đó.
Định luật thứ ba[sửa]
- Xem chi tiết: Định luật thứ ba của Newton
Định luật thứ ba của Newton là kết quả của áp dụng tính đối xứng cho trường hợp khi lực có ảnh hưởng đáng kể lên các vật khác nhau. Định luật thứ ba có nghĩa là mọi lực là sự tương tác giữa các vật với nhau,[12][Note 3] và do vậy không có thứ như lực vô hướng hay lực tác dụng chỉ lên một vật. Bất cứ khi nào vật thứ nhất tác dụng lực F lên vật thứ hai, vật thứ hai sẽ tác dụng lực −F lên vật thứ nhất. F và −F có độ lớn bằng nhau nhưng ngược hướng. Định luật này đôi khi còn gọi là định luật tác dụng-phản tác dụng, với F gọi là "tác dụng" và −F là "phản tác dụng". Tác dụng và phản tác dụng là đồng thời:
Nếu vật 1 và vật 2 được coi trong cùng một hệ, khi đó hợp lực tác dụng lên hệ do sự tương tác giữa vật 1 và 2 là bằng 0 do
Điều này có nghĩa là trong hệ kín gồm các hạt, không có nội lực mất cân bằng. Tức là, lực tác dụng-phản tác dụng giữa bất kì hai vật nào trong hệ kín sẽ không làm gia tốc khối tâm của hệ. Các vật trong hệ chỉ gia tốc tương đối với nhau, trong khi về tổng thể thì cả hệ không bị gia tốc. Hay cách khác, nếu có ngoại lực tác dụng lên hệ, thì khối tâm của hệ sẽ chịu sự gia tốc bằng độ lớn của ngoại lực chia cho khối lượng của cả hệ.[1]Bản mẫu:Rp[3]
Kết hợp định luật hai và ba của Newton, có thể chứng tỏ được rằng động lượng của một hệ là bảo toàn. Sử dụng
và tích phân theo thời gian, thu được phương trình:
Đối với hệ bao gồm vật 1 và 2,
tức là động lượng được bảo toàn.[13] Lập luận tương tự, có thể tổng quát hóa kết quả cho hệ chứa số lượng hạt bất kỳ. Điều này cũng chỉ ra rằng động lượng trao đổi giữa các hạt sẽ không ảnh hưởng đến tổng động lượng của cả hệ. Nói chung, khi coi tất cả lực là do tương tác giữa khối lượng các vật (như bỏ qua lực điện từ), có thể xác định một hệ với tổng động lượng bảo toàn.[1][3]
Theo thuyết tương đối hẹp[sửa]
Trong thuyết tương đối hẹp, khối lượng và năng lượng là tương đương với nhau qua công thức E = mc2 (như khi tính toán công cần thiết để gia tốc một vật). Khi vận tốc của vật tăng lên, thì năng lượng của nó cũng tăng và do vậy khối lượng cũng tăng tương đương (quán tính). Do vậy cần nhiều lực hơn để gia tốc nó so với khi vật có vận tốc nhỏ. Định luật hai của Newton viết dưới dạng
vẫn còn đúng theo định nghĩa toán học.[14]Bản mẫu:Rp Nhưng để bảo toàn, động lượng tương đối tính phải được định nghĩa lại thành:
với
-
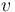 là
vận
tốc
là
vận
tốc -
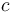 là
tốc
độ
ánh
sáng
là
tốc
độ
ánh
sáng -
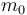 là
khối
lượng
nghỉ.
là
khối
lượng
nghỉ.
Biểu
thức
tương
đối
tính
liên
hệ
lực
và
gia
tốc
cho
một
hạt
với
khối
lượng
nghỉ
không
đổi
khác
0
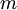 chuyển
động
theo
hướng
chuyển
động
theo
hướng
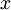 là:
là:
trong đó hệ số Lorentz
Trong
giai
đoạn
đầu
của
thuyết
tương
đối
đặc
biệt,
biểu
thức
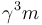 và
và
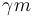 được
gọi
là
khối
lượng
theo
phương
dọc
và
phương
ngang.
Lực
tương
đối
tính
không
tạo
ra
gia
tốc
đều,
mà
gia
tốc
của
vật
giảm
khi
vận
tốc
của
nó
tiệm
cận
đến
tốc
độ
ánh
sáng.
Lưu
ý
rằng
được
gọi
là
khối
lượng
theo
phương
dọc
và
phương
ngang.
Lực
tương
đối
tính
không
tạo
ra
gia
tốc
đều,
mà
gia
tốc
của
vật
giảm
khi
vận
tốc
của
nó
tiệm
cận
đến
tốc
độ
ánh
sáng.
Lưu
ý
rằng
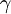 không
xác
định
đối
với
vật
có
khối
lượng
nghỉ
khác
0
tại
vận
tốc
ánh
sáng,
và
lý
thuyết
tương
đối
không
cho
một
tiên
đoán
nào
về
vật
tại
vận
tốc
này.
không
xác
định
đối
với
vật
có
khối
lượng
nghỉ
khác
0
tại
vận
tốc
ánh
sáng,
và
lý
thuyết
tương
đối
không
cho
một
tiên
đoán
nào
về
vật
tại
vận
tốc
này.
Có thể viết lại định nghĩa lực theo thuyết tương đối như sau
bằng
cách
sử
dụng
vectơ-4.
Biểu
thức
này
đúng
trong
thuyết
tương
đối
khi
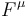 là
lực-4,
là
lực-4,
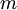 là
khối
lượng
bất
biến,
và
là
khối
lượng
bất
biến,
và
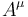 là
gia
tốc-4.[16]
là
gia
tốc-4.[16]
Miêu tả[sửa]
Do cách nhận thức lực thông qua những tác dụng như đẩy hoặc kéo, điều này mang lại cách hiểu trực giác khi miêu tả lực.[4] Như những khái niệm vật lý khác (ví dụ nhiệt độ), cách hiểu trực giác về lực được lượng hóa nhờ sử dụng định nghĩa miêu tả chính xác (operational definition) mà nó nhất quán trực tiếp với kết quả quan sát và phạm vi đo tiêu chuẩn. Thông qua thí nghiệm, các nhà vật lý xác định được rằng lực đo trong phòng thí nghiệm là hoàn toàn thống nhất với lực định nghĩa trong cơ học Newton.
Lực tác dụng theo một hướng cụ thể với độ lớn phụ thuộc vào sự kéo hay đẩy đi mạnh bao nhiêu. Bởi những đặc tính này, lực được phân loại thành đại lượng "vectơ". Điều này có nghĩa rằng lực tuân theo một bộ các quy tắc toán học khác với các đại lượng vật lý không có hướng (đại lượng vô hướng). Ví dụ, khi xác định kết quả của hai lực tác dụng lên cùng một vật, cần phải biết rõ độ lớn và hướng của từng lực nhằm tính toán ra hợp lực. Chỉ cần thiếu một trong hai thông tin này ở mỗi lực thì tình huống sẽ trở lên mập mờ. Như nếu bạn biết hai người đang kéo cùng một sợi dây mà đã biết độ lớn lực kéo nhưng bạn lại không biết mỗi người kéo theo hướng nào, thì bạn sẽ không thể xác định được gia tốc của sợi dây là bao nhiêu. Hai người có thể kéo theo hai hướng ngược nhau như trong trò kéo co hoặc hai người cùng kéo về một hướng. Trong ví dụ một chiều đơn giản này, nếu không biết hướng của lực thì sẽ không thể biết được tổng hợp lực là kết quả của việc cộng hay trừ độ lớn của hai lực. Lực gắn với khái niệm vectơ cho phép tránh được những khó khăn này.
Về mặt lịch sử, các nhà khoa học nghiên cứu lực trong điều kiện cân bằng tĩnh đầu tiên khi ấy một vài lực có thể triệt tiêu lẫn nhau. Các thí nghiệm này minh hóa tính chất quan trọng của lực đó là đại lượng vectơ cộng được: chúng có độ lớn và hướng.[4] Khi hai lực tác dụng vào cùng một hạt điểm, lực kết quả, hợp lực (hoặc tổng hợp lực), sẽ được xác định tuân theo quy tắc hình bình hành của phép cộng vectơ: mỗi lực được biểu thị bằng với 2 cạnh chung đỉnh của hình bình hành, và hợp lực chính bằng vectơ với độ lớn bằng đường chéo của hình bình hành và hướng dọc theo cạnh đó.[1][3] Độ lớn của hợp lực phụ thuộc vào góc hợp bởi hai lực cũng như độ lớn của mỗi lực thành phần. Nếu hai lực tác dụng lên một vật, quy tắc hình bình hành chỉ áp dụng được khi đường kéo dài hai lực cắt nhau.
Biểu đồ lực là một cách thuận tiện nhằm thu được lực tổng hợp. Về mặt lý thuyết, các biểu đồ này được vẽ với bảo tồn góc và độ lớn tương đối của các vectơ lực sao cho có thể thực hiện được phép cộng hình học vectơ.[17]
Không những cộng được, lực cũng có thể phân tích thành các lực thành phần mà từng cặp vuông góc với nhau. Một lực chỉ theo hướng đông bắc có thể phân tích thành hai lực, một lực chỉ theo hướng bắc còn lực kia chỉ theo hướng đông. Tổng của hai lực thành phần này tuân theo phép cộng vectơ sẽ thu được lực ban đầu. Việc phân tích vectơ lực theo hệ các vectơ cơ sở thường là một phương pháp toán học rõ ràng nhằm miêu tả lực hơn là miêu tả nó bằng độ lớn và hướng.[18] Điều này là do, đối với các thành phần trực giao, các thành phần của vectơ tổng được xác định một cách duy nhất bằng cách cộng các độ lớn của từng các vectơ riêng rẽ. Các thành phần trực giao là độc lập với nhau do lực tác dụng theo hướng 90° sẽ không có ảnh hưởng đến lực vuông góc với nó. Việc chọn bộ các vectơ cơ sở trực giao sao cho để việc thực hiện các phép toán là thuận tiện nhất. Cách hay gặp là chọn cơ sở vectơ theo cùng hướng với một trong những lực cần phân tích, do lực đó sẽ chỉ có một thành phần khác 0 theo hệ cơ sở đó. Các vectơ lực trực giao có thể là một bộ ba trong không gian 3 chiều, với mỗi cặp vectơ cơ sở trực giao với nhau.[1][3]
Cân bằng[sửa]
Cân bằng cơ học xuất hiện khi hợp lực tác dụng lên một điểm bằng 0 (hay tổng các vectơ lực bằng 0). Khi mở rộng sang cho vật thực, cần thêm một điều kiện nữa là tổng mô men lực cũng phải bằng 0.
Có hai loại cân bằng là cân bằng tĩnh và cân bằng động.
Trạng thái cân bằng[sửa]
- Xem chi tiết: Tĩnh học
Các nhà khoa học hiểu khá tốt về trạng thái cân bằng tĩnh trước khi cơ học cổ điển ra đời. Các vật đứng yên sẽ có tổng hợp lực tác dụng lên nó bằng 0.[19]
Trường hợp đơn giản nhất của cân bằng tĩnh là khi hai lực có độ lớn bằng nhau nhưng ngược hướng nhau tác dụng tại một điểm. Ví dụ, một vật nằm trên mặt phẳng bị kéo (hút) về tâm Trái Đất bởi lực hấp dẫn. Cùng lúc đó, lực bề mặt chống lại bằng một lực hướng lên trên (còn gọi là lực pháp tuyến). Kết quả là hợp lực bằng 0 và vật không chịu sự gia tốc.[4]
Trường hợp đẩy hay kéo một vật có tính tới ma sát bề mặt khiến cho vật không di chuyển được bởi vì lực tác dụng vào bị chống lại bởi ma sát tĩnh (hay ma sát nghỉ), tạo ra giữa vật và bề mặt nó nằm lên. Khi vật không di chuyển, lực ma sát tĩnh cân bằng chính xác với lực tác dụng và hợp lực bằng 0. Ma sát tĩnh tăng hoặc giảm nhằm đáp ứng lại lực tác dụng vào cho tới một giới hạn trên xác định bởi đặc tính của bề mặt tiếp xúc và vật thể đó.[4]
Ứng dụng cân bằng tĩnh giữa hai lực là một cách thông dụng nhất nhằm đo lực, sử dụng các thiết bị đơn giản như cân trọng lượng (weighing scales) và cân lò xo. Ví dụ, một vật treo lên một cân lò xo thẳng đứng sẽ chịu tác dụng của lực hấp dẫn và một lực cân bằng do sự đàn hồi của lò xo mà tỷ lệ với trọng lượng của vật. Sử dụng những công cụ này, một số định luật liên quan đến lực đã được khám phá: lực hấp dẫn tỉ lệ với thể tích vật chiếm chỗ trong chất lỏng hay định luật Archimedes; nguyên lý đòn bẩy của Archimedes; định luật Boyle-Mariotte cho áp suất khí; và định luật Hooke đối với lò xo. Tất cả đều được khám phá và xác nhận bằng thí nghiệm trước khi Newton nêu ra ba định luật về chuyển động của ông.[1][3][4]
Động lực học[sửa]
- Xem chi tiết: Động lực học
Galileo là người đầu tiên miêu tả về cân bằng động học khi ông nhận thấy rằng một số giả sử của Aristotel mâu thuẫn với quan sát và tính logic. Galileo nhận thấy rằng phép cộng vận tốc đơn giản dẫn đến đòi hỏi một "hệ quy chiếu đứng yên tuyệt đối" là không cần thiết. Ông kết luận rằng trạng thái chuyển động đều hoàn toàn tương đương với trạng thái đứng yên. Điều này mâu thuẫn với khái niệm của Aristotle về "trạng thái tự nhiên" của sự đứng yên mà các vật với khối lượng sẽ cuối cùng đạt đến một cách tự nhiên. Các thí nghiệm đơn giản chứng tỏ rằng nhận thức của Galileo về sự tương đương giữa chuyển động đều và trạng thái đứng yên là đúng đắn. Ví dụ, nếu một người đứng trên con thuyền đi với vận tốc không đổi và thả rơi một quả bóng, khi ấy Aristotel cho rằng quả bóng sẽ rơi về phía sau người đó khi con thuyền tiến về phía trước. Tuy nhiên, thực tế thì quả bóng vẫn rơi đúng tại chân người đó hệt như khi người đó đứng yên trên mặt đất. Do không có lực tác dụng theo phương ngang nào khi quả bóng rơi, chỉ có thể kết luận rằng quả bóng tiếp tục di chuyển với cùng vận tốc như con thuyền khi nó rơi. Do vậy không cần một lực nào để duy trì quả bóng di chuyển với cùng vận tốc của con thuyền về phía trước.[20]
Hơn nữa bất kỳ vật nào chuyển động với vận tốc đều thì hợp lực tác dụng vào nó phải bằng 0. Đây chính là định nghĩa của cân bằng động: khi mọi lực tác dụng lên một vật sẽ cân bằng sao cho vật đó vẫn chuyển động với vận tốc không đổi.
Một trường hợp đơn giản của cân bằng động đó là vật chuyển động đều trên bề mặt với ma sát động. Trong trường hợp này, lực tác dụng theo hướng chuyển động trong khi lực ma sát động tác dụng theo hướng ngược lại. Kết quả là tổng hợp lực bằng 0, nhưng do từ đầu vật chuyển động với vận tốc không đổi, do vậy vật tiếp tục di chuyển với vận tốc đều đó. Aristotle đã hiểu sai về chuyển động đều khi không nhận ra được sự có mặt của ma sát động giữa các bề mặt.[1][3]
Biểu đồ Feynman[sửa]
- Xem chi tiết: Biểu đồ Feynman
Trong vật lý hạt hiện đại, lực và sự gia tốc của các hạt được giải thích như là sản phẩm toán học của sự trao đổi các boson gauge mang động lượng. Cùng với sự phát triển của lý thuyết trường lượng tử và thuyết tương đối rộng, các nhà vật lý nhận ra rằng lực một khái niệm phái sinh từ định luật bảo toàn động lượng (4-động lượng trong thuyết tương đối và động lượng của các hạt ảo trong điện động lực học lượng tử). Sự bảo toàn động lượng, mà có thể suy trực tiếp từ tính đối xứng đồng nhất của không gian và thường được coi là khái niệm cơ bản hơn khái niệm lực. Do vậy tên gọi các "lực cơ bản" được các nhà vật lý gọi lại một cách chính xác hơn là "tương tác cơ bản".[6]Bản mẫu:Rp Khi hạt A phát (tạo ra) hoặc hấp thụ (hủy) hạt ảo B, hạt A sẽ bị giật lùi do hệ quả của định luật bảo toàn động lượng dẫn đến sự liên tưởng là hạt A bị hút hoặc đẩy bằng cách trao đổi thông qua hạt B. Cách miêu tả này áp dụng đối với mọi lực trong tương tác cơ bản. Trong khi cần có những miêu tả bằng toán học phức tạp về các tương tác này một cách chi tiết và cho kết quả chính xác, có một cách dễ hình dung nhằm minh họa các tương tác cơ bản thông qua biểu đồ Feynman. Trong biểu đồ Feynman, mỗi hạt vật chất được biểu diễn bằng một đường thẳng (xem tuyến thế giới (world line)) di chuyển trong không thời gian theo hướng đi lên hoặc chếch sang phải trong biểu đồ. Vật chất và phản vật chất là giống nhau ngoại trừ hướng lan truyền của chúng trên biểu đồ Feynman. Các tuyến thế giới của các hạt cắt nhau tại các đỉnh, và biểu đồ Feynman thể hiện lực xuất hiện từ một tương tác tại mỗi đỉnh thông qua sự thay đổi tức thì trong hướng của tuyến thế giới của hạt. Các boson gauge phát ra từ đỉnh dưới dạng đường lượn sóng, và trong trường hợp trao đổi hạt ảo, chúng bị hấp thụ tại đỉnh kế tiếp.[21]
Tính hữu dụng của biểu đồ Feynman ở chỗ các hiện tượng vật lý khác trong bức tranh chung của tương tác cơ bản nhưng về mặt khái niệm khác hẳn với khái niệm lực vẫn được miêu tả trong cùng các quy tắc của biểu đồ. Ví dụ, biểu đồ Feynman có thể miêu tả súc tích một cách chi tiết tiến trình một hạt neutron phân rã thành một electron, proton, và phản neutrino electron, tương tác được truyền bởi cùng boson gauge của tương tác yếu.[21]
Lực cơ bản[sửa]
- Xem chi tiết: Tương tác cơ bản
Mọi hoạt động trong vũ trụ đều được miêu tả thu gọn về các tương tác cơ bản. Lực mạnh và yếu là các lực hạt nhân có tầm tác dụng rất ngắn ở thang vi mô, chúng chịu trách nhiệm trong tương tác giữa các hạt hạ nguyên tử, bao gồm các nucleon và hạt nhân nguyên tử. Lực điện từ tác dụng giữa các hạt điện tích, và lực hấp dẫn tác động đến mọi hạt khối lượng. Ví dụ, ma sát là thuộc tính thể hiện của lực điện từ tác dụng giữa các nguyên tử tại hai bề mặt tiếp giáp nhau, kết hợp với nguyên lý loại trừ Pauli,[22] ngăn cản các nguyên tử đi xuyên qua nhau. Tương tự, lực đàn hồi từ các lò xo, như mô hình hóa bởi định luật Hooke, là kết quả của lực điện từ và nguyên lý loại trừ kết hợp với nhau tác dụng vào vật làm cho nó trở về vị trí cân bằng. Lực ly tâm là lực gia tốc xuất hiện từ sự gia tốc của một hệ quy chiếu quay.[1]Bản mẫu:Rp[3]Bản mẫu:Rp
Sự phát triển của các lý thuyết miêu tả lực cơ bản đi theo hướng thống nhất các khái niệm mà ban đầu có vẻ như tách biệt nhau. Ví như Isaac Newton đã thống nhất lực làm cho các vật rơi trở lại mặt đất với lực gây ra chuyển động của các hành tinh quanh Mặt Trời trong cơ học thiên thể thông qua định luật vạn vật hấp dẫn của ông. Michael Faraday và James Clerk Maxwell chứng tỏ rằng lực điện và lực từ là hai biểu hiện của cùng một lực điện từ. Trong thế kỷ 20, sự ra đời của cơ học lượng tử dẫn tới những hiểu biết hiện đại về ba lực cơ bản trong tự nhiên (ngoại trừ hấp dẫn) là do tương tác giữa vật chất (fermion) thông qua trao đổi các hạt ảo gọi là boson gauge.[23] Mô hình chuẩn của vật lý hạt đưa các nhà vật lý đi đến tiên đoán về sự thống nhất giữa tương tác yếu và tương tác điện từ trong lý thuyết điện yếu và các tiên đoán của lý thuyết này đã được xác nhận bằng thực nghiệm. Mô hình chuẩn cũng tiên đoán sự tồn tại của hạt chịu trách nhiệm sinh khối lượng cho các hạt khác thông qua cơ chế Higgs mà gần đây được khám phá tại CERN, nhưng mô hình chuẩn cũng chưa giải thích được tại sao neutrino dao động (hay neutrino thực sự có khối lượng rất nhỏ). Lý thuyết thống nhất lớn miêu tả sự kết hợp của tương tác điện yếu với tương tác mạnh cũng như có một số lý thuyết về siêu đối xứng nhằm giải quyết một số vấn đề chưa giải được trong vật lý học. Các nhà vật lý vẫn đang cố gắng tìm cách phát triển một lý thuyết thống nhất nhất quán kết hợp bốn tương tác cơ bản trong một lý thuyết gọi là thuyết của mọi thứ. Einstein đã thử và không thành công trên con đường này, và hiện nay có một số lý thuyết nổi bật như lý thuyết dây nhằm trả lời các vấn đề này.[6]Bản mẫu:Rp
Lực hấp dẫn[sửa]
- Xem chi tiết: Tương tác hấp dẫn
Người
ta
đã
không
nhận
ra
lực
hấp
dẫn
là
một
lực
phổ
quát
cho
đến
tận
khi
Isaac
Newton
nghiên
cứu
nó.
Trước
Newton,
xu
hướng
các
vật
rơi
xuống
bề
mặt
Trái
Đất
không
được
hiểu
là
có
liên
quan
đến
chuyển
động
của
các
thiên
thể.
Galileo
đã
làm
thí
nghiệm
nhằm
nghiên
cứu
đặc
tính
của
các
vật
thả
rơi
bằng
cách
ông
miêu
tả
gia
tốc
của
mọi
vật
rơi
tụ
do
là
hằng
số
và
độc
lập
với
khối
lượng
của
vật.
Ngày
nay,
gia
tốc
do
lực
hấp
dẫn
về
phía
bề
mặt
Trái
Đất
thường
được
ký
hiệu
là
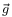 và
có
độ
lớn
khoảng
9,81
mét
trên
giây
bình
phương
(giá
trị
này
đo
tại
mức
nước
biển
và
có
thể
thay
đổi
phụ
thuộc
vào
vị
trí),
và
vectơ
này
hướng
về
tâm
Trái
Đất.[24]
Quan
sát
này
có
nghĩa
là
lực
hấp
dẫn
tác
động
lên
vật
tại
bề
mặt
Trái
Đất
tỷ
lệ
trực
tiếp
với
khối
lượng
của
vật.
Do
vậy
một
vật
có
khối
lượng
và
có
độ
lớn
khoảng
9,81
mét
trên
giây
bình
phương
(giá
trị
này
đo
tại
mức
nước
biển
và
có
thể
thay
đổi
phụ
thuộc
vào
vị
trí),
và
vectơ
này
hướng
về
tâm
Trái
Đất.[24]
Quan
sát
này
có
nghĩa
là
lực
hấp
dẫn
tác
động
lên
vật
tại
bề
mặt
Trái
Đất
tỷ
lệ
trực
tiếp
với
khối
lượng
của
vật.
Do
vậy
một
vật
có
khối
lượng
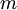 sẽ
chịu
một
lực:
sẽ
chịu
một
lực:
Trong trường hợp rơi tự do, không có lực cản lại lực hấp dẫn và do vậy tổng hợp lực tác dụng lên vật chính là trọng lượng của nó. Đối với các vật không trong trạng thái rơi tự do, lực hấp dẫn cân bằng với lực tác dụng lên vật theo hướng ngược lại. Ví dụ, một người đứng trên mặt đất sẽ chịu tổng hợp lực tác dụng vào anh ta bằng 0, do trọng lượng của anh ta cân bằng với lực pháp tuyến tác dụng bởi mặt đất.[1][3]
Công lao của Newton trong định luật vạn vật hấp dẫn đó là thống nhất chuyển động của các thiên thể, mà Aristotle cho rằng chúng trong trạng thái tự nhiên của chuyển động đều, với chuyển động rơi tự do của các vật trên Trái Đất. Từ định luật của ông cũng suy ra được các định luật của Kepler miêu tả chuyển động của các thiên thể có từ trước đó.[25]
Newton
nhận
ra
rằng
ảnh
hưởng
của
hấp
dẫn
có
thể
quan
sát
theo
nhiều
cách
khác
nhau
ở
những
khoảng
cách
lớn
hơn.
Đặc
biệt,
ông
chứng
tỏ
rằng
gia
tốc
của
Mặt
Trăng
trên
quỹ
đạo
quanh
Trái
Đất
có
thể
được
gắn
cho
bởi
nguyên
nhân
của
cùng
một
lực
hấp
dẫn
nếu
như
gia
tốc
do
hấp
dẫn
giảm
tuân
theo
định
luật
nghịch
đảo
bình
phương.
Hơn
nữa,
Newton
cũng
thấy
gia
tốc
do
hấp
dẫn
tỷ
lệ
với
khối
lượng
của
vật
thể
hút.[25]
Kết
hợp
những
suy
nghĩ
này
ông
dẫn
ra
được
công
thức
liên
hệ
khối
lượng
(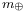 )
và
bán
kính
(
)
và
bán
kính
(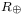 )
của
Trái
Đất
với
gia
tốc
hấp
dẫn:
)
của
Trái
Đất
với
gia
tốc
hấp
dẫn:
với
hướng
của
vectơ
theo
hướng
của
vectơ
đơn
vị
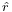 mà
hướng
từ
tâm
Trái
Đất
ra
ngoài.[7]
mà
hướng
từ
tâm
Trái
Đất
ra
ngoài.[7]
Trong
phương
trình
này,
hằng
số
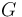 được
đưa
ra
nhằm
miêu
tả
độ
mạnh
của
lực
hấp
dẫn.
Hằng
số
này
còn
gọi
là
hằng
số
hấp
dẫn
Newton,[26]
mặc
dù
thời
Newton
người
ta
chưa
xác
định
được
nó.
Cho
đến
tận
năm
1798
Henry
Cavendish
mới
lần
đầu
tiên
có
thể
xác
định
được
giá
trị
của
được
đưa
ra
nhằm
miêu
tả
độ
mạnh
của
lực
hấp
dẫn.
Hằng
số
này
còn
gọi
là
hằng
số
hấp
dẫn
Newton,[26]
mặc
dù
thời
Newton
người
ta
chưa
xác
định
được
nó.
Cho
đến
tận
năm
1798
Henry
Cavendish
mới
lần
đầu
tiên
có
thể
xác
định
được
giá
trị
của
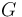 bằng
thí
nghiệm
cân
xoắn
thăng
bằng;
thí
nghiệm
này
nhanh
chóng
trở
lên
nổi
tiếng
khi
việc
xác
định
được
giá
trị
của
bằng
thí
nghiệm
cân
xoắn
thăng
bằng;
thí
nghiệm
này
nhanh
chóng
trở
lên
nổi
tiếng
khi
việc
xác
định
được
giá
trị
của
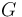 cũng
đồng
nghĩa
với
việc
xác
định
được
khối
lượng
của
Trái
Đất.
Đi
xa
hơn,
Newton
còn
nhận
thấy
do
mọi
thiên
thể
tuân
theo
cùng
các
định
luật
của
Kepler,
do
vậy
định
luật
hấp
dẫn
của
ông
phải
mang
tính
phổ
quát.
Định
luật
vạn
vật
hấp
dẫn
của
Newton
phát
biểu
rằng
lực
tác
dụng
lên
một
khối
cầu
khối
lượng
cũng
đồng
nghĩa
với
việc
xác
định
được
khối
lượng
của
Trái
Đất.
Đi
xa
hơn,
Newton
còn
nhận
thấy
do
mọi
thiên
thể
tuân
theo
cùng
các
định
luật
của
Kepler,
do
vậy
định
luật
hấp
dẫn
của
ông
phải
mang
tính
phổ
quát.
Định
luật
vạn
vật
hấp
dẫn
của
Newton
phát
biểu
rằng
lực
tác
dụng
lên
một
khối
cầu
khối
lượng
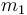 do
sức
hút
hấp
dẫn
từ
khối
cầu
khối
lượng
do
sức
hút
hấp
dẫn
từ
khối
cầu
khối
lượng
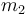 bằng
bằng
với
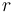 là
khoảng
cách
giữa
tâm
hai
khối
cầu
và
là
khoảng
cách
giữa
tâm
hai
khối
cầu
và
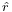 là
vectơ
đơn
vị
chỉ
theo
hướng
từ
tâm
của
vật
thể
đầu
tiên
đến
tâm
của
vật
thể
thứ
hai.[7]
là
vectơ
đơn
vị
chỉ
theo
hướng
từ
tâm
của
vật
thể
đầu
tiên
đến
tâm
của
vật
thể
thứ
hai.[7]
Định luật này đã đứng vững trong hơn 200 năm như là cơ sở cho những miêu tả của cơ học thiên thể cho đến đầu thế kỷ 20. Trong thời gian này, phương pháp phức tạp của lý thuyết nhiễu loạn[27] đã được phát minh nhằm tính toán những sai lệch trong quỹ đạo của thiên thể trong bài toán nhiều vật như hệ hành tinh, vệ tinh tự nhiên, sao chổi, hay tiểu hành tinh. Phương pháp này đủ chính xác để giúp các nhà thiên văn học tiên đoán sự tồn tại của Sao Hải Vương trước khi họ quan sát thấy nó.[28]
Chỉ có quỹ đạo của Sao Thủy là định luật của Newton dường như không thể giải thích một cách tốt nhất. Một số nhà thiên văn đề xuất có sự tồn tại của một hành tinh nằm bên trong quỹ đạo giữa Sao Thủy và Mặt Trời nhằm miêu tả chuyển động dị thường của sự tiến động của điểm cận nhật quỹ đạo Sao Thủy; tuy vậy không có một hành tinh nào được phát hiện ra. Khi Albert Einstein cuối cùng thiết lập ra thuyết tương đối tổng quát (GR) ông đã nghĩ ngay tới khải năng giải thích chuyển động dị thường của Sao Thủy bằng lý thuyết mới này. Kết quả tiên đoán của thuyết tương đối rộng khớp với các số liệu quan sát khiến Einstein tin rằng ông đã tìm ra dạng đúng của phương trình trường. Đây là lần đầu tiên lý thuyết hấp dẫn của Newton được chỉ ra là ít chính xác hơn một lý thuyết khác.[29]
Kể từ đó, thuyết tương đối rộng được công nhận là lý thuyết tốt nhất miêu tả được lực hấp dẫn. Trong thuyết tương đối rộng, lực hấp dẫn không được xem như là một lực, bởi chuyển động rơi tự do của vật trong trường hấp dẫn đi theo đường trắc địa trong không thời gian cong – hay là đường ngắn nhất giữa hai sự kiện trong không thời gian. Từ vật rơi tự do, mọi chuyển động xảy ra dường như không phải do lực hấp dẫn bên ngoài tác động hay không còn lực hấp dẫn. Chỉ khi nhận xét trên tổng thể cả hệ, độ cong của không thời gian mới có thể nhận thấy và lực xuất hiện như là một cách giải thích cho vật đi theo những quỹ đạo cong. Do vậy, đường thẳng trong không thời gian tương ứng với đường cong trong không gian, hay quỹ đạo đường đạn của vật. Ví dụ, một quả bóng rổ ném lên từ mặt đất sẽ chuyển động theo quỹ đạo hình parabol trong trường hấp dẫn đều. Quỹ đạo trong không thời gian của nó (khi tính tới chiều thời gian ct) sẽ là một đường gần thẳng, hơi cong (với bán kính cong có độ lớn tới vài năm ánh sáng). Kết quả của đạo hàm thời gian của động lượng của vật được đồng nhất với "lực hấp dẫn".[3]
Lực điện từ[sửa]
- Xem chi tiết: Tương tác điện từ
Lực điện từ được miêu tả lần đầu tiên vào năm 1784 bởi Coulomb khi ông coi có một lực tồn tại tác dụng lên giữa hai điện tích.[14]Bản mẫu:Rp Tính chất của lực tĩnh điện đó là nó tuân theo định luật nghịch đảo bình phương khoảng cách giữa hai điện tích, và đều có dạng hút và dạng đẩy (sự phân cực điện), đồng thời lực điện độc lập với khối lượng của vật tích điện cũng như tuân theo nguyên lý chồng chập. Định luật Coulomb đã thống nhất được mọi quan sát này trong một phát biểu duy nhất.[30]
Các nhà toán học và vật lý sau đó đã tìm ra cách định nghĩa xây dựng cho điện trường một cách hữu ích nhằm xác định được lực tĩnh điện tác động lên một điện tích tại mọi điểm trong không gian. Định nghĩa điện trường dựa trên giả sử có một điện tích thử tồn tại trong điện trường và sau đó dựa trên định luật Coulomb để xác định được lực của điện trường tác dụng lên điện tích thử và suy ra được cường độ điện trường tại vị trí của điện tích thử.[31]Bản mẫu:Rp Do vậy điện trường trong không gian được định nghĩa như là
với
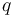 là
độ
lớn
của
điện
tích
thử.
là
độ
lớn
của
điện
tích
thử.
Trong khi đó, người ta cũng phát hiện ra lực Lorentz của một nam châm tồn tại giữa hai dây dẫn mang dòng điện. Nó có cùng một tính chất toán học như định luật Coulomb khi mà các dây điện có thể hút hoặc đẩy lẫn nhau tùy thuộc vào chiều của dòng điện chạy trong mỗi sợi dây. Tương tự như điện trường, từ trường được dùng để xác định lực từ tác dụng lên một dây dẫn điện tại một điểm bất kỳ trong không gian. Tương tự rong trường hợp này, độ lớn của từ trường sẽ được xác định là
với
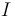 là
độ
lớn
của
dòng
điện
chạy
qua
dây
dẫn
và
là
độ
lớn
của
dòng
điện
chạy
qua
dây
dẫn
và
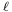 là
độ
dài
của
dây
mà
dòng
điện
thử
nghiệm
chạy
qua.
Từ
trường
tác
dụng
một
lực
lên
mọi
nam
châm
như
từ
trường
Trái
Đất
tác
dụng
lên
kim
la
bàn
và
được
các
nhà
hàng
hải,
hoa
tiêu
sử
dụng
để
định
vị
phương
hướng.
là
độ
dài
của
dây
mà
dòng
điện
thử
nghiệm
chạy
qua.
Từ
trường
tác
dụng
một
lực
lên
mọi
nam
châm
như
từ
trường
Trái
Đất
tác
dụng
lên
kim
la
bàn
và
được
các
nhà
hàng
hải,
hoa
tiêu
sử
dụng
để
định
vị
phương
hướng.
Thông qua kết hợp định nghĩa của dòng điện bằng sự biến đổi theo thời gian của các hạt điện tích chạy trong dây dẫn, Lorentz nêu ra quy tắc tích vectơ xác định lực Lorentz miêu tả lực tác dụng lên một điện tích di chuyển trong từ trường.[31] Sự liên hệ giữa điện học và từ học cho phép miêu tả một cách thống nhất lực điện từ tác dụng lên điện tích. Lực này có thể biểu diễn dưới dạng tổng của lực tĩnh điện (do tác động của điện trường) và lực từ (do từ trường):
với
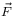 lực
điện
từ,
lực
điện
từ,
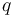 là
độ
lớn
điện
tích
của
hạt
thử,
là
độ
lớn
điện
tích
của
hạt
thử,
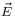 là
điện
trường,
là
điện
trường,
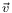 là
vận
tốc
của
hạt
nhân
với
từ
trường
(
là
vận
tốc
của
hạt
nhân
với
từ
trường
(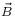 ).
).
Nguồn gốc của điện trường và từ trường không được hiểu đầy đủ cho đến tận năm 1864 khi James Clerk Maxwell thống nhất một số các lý thuyết trước đó trong một hệ 20 phương trình vô hướng, mà sau đó Oliver Heaviside độc lập với Josiah Willard Gibbs viết lại thành hệ 4 phương trình vectơ.[32] "Phương trình Maxwell" miêu tả đầy đủ nguồn gốc của trường điện từ đứng yên hay chuyển động, cũng như tương tác giữa chúng. Điều này dẫn Maxwell tới khám phá ra rằng từ trường và điện trường có thể tự duy trì lẫn nhau trong không gian dưới dạng sóng lan truyền với tốc độ mà ông tính ra được bằng tốc độ ánh sáng. Ý nghĩa này mang lại sự thống nhất của ngành điện từ học non trẻ với ngành quang học cũng như dẫn trực tiếp tới sự miêu tả đầy đủ hơn về phổ điện từ.[33]
Tuy nhiên, lý thuyết của Maxwell đã không giải thích được hai hiện tượng quan sát vào thời đó, hiệu ứng quang điện, và sự không tồn tại của thảm họa cực tím. Hai hiện tượng này đã thúc đẩy các nhà vật lý hàng đầu đi đến một lý thuyết điện từ mới dựa trên cơ học lượng tử: điện động lực học lượng tử (QED), lý thuyết miêu tả một cách trọn vẹn các hiệu ứng điện từ khi có sự tham gia của hạt trung gian là các photon thực và ảo. Trong QED, photon là các hạt trao đổi trong tương tác liên quan đến điện từ bao gồm lực điện từ.[Note 4]
Có một sự hiểu nhầm phổ biến khi cho rằng độ cứng và rắn của chất rắn là do lực đẩy điện từ giữa các điện tích cùng dấu. Tuy nhiên, tính cứng và rắn của vật chất là hệ quả từ nguyên lý loại trừ Pauli.Bản mẫu:Citation needed Do electron là các fermion, chúng không thể ở cùng một trạng thái lượng tử. Khi các electron trong nguyên tử bị nén chặt lại, sẽ không có đủ trạng thái cơ lượng tử năng lượng thấp cho mọi electron (và là một trong những hệ quả của nguyên lý bất định), do đó một số electron phải ở trạng thái năng lượng cao hơn. Điều này có nghĩa là cần có nhiều năng lượng hơn để nén chúng lại. Trong khi đó, đối với từng nguyên tử thì chỉ có một số hữu hạn số trạng thái mà các electron có thể chiếm giữ trên obitan nguyên tử.
Lực hạt nhân[sửa]
- Xem chi tiết: Lực hạt nhân
Có hai loại "lực hạt nhân" mà ngày nay được coi là các tương tác miêu tả bởi các lý thuyết trường lượng tử trong vật lý hạt. Lực hạt nhân mạnh[14]Bản mẫu:Rp là lực chịu trách nhiệm cho cấu trúc tổ hợp của các nucleon và hạt nhân nguyên tử trong khi lực hạt nhân yếu[14]Bản mẫu:Rp gây ra sự phân rã của một số nucleon và hạt nhân thành các lepton và các hạt hadron khác.[1][3]
Lực hạt nhân mạnh là tương tác giữa các quark và gluon cũng như liên kết các proton và neutron với nhau, như được miêu tả trong thuyết sắc động lực học lượng tử (QCD).[34] Các hạt gluon là những hạt truyền tương tác mạnh, tác dụng lên các quark, phản quark, và chính gluon. Lực mạnh là lực có cường độ mạnh nhất trong bốn lực cơ bản trong tự nhiên.
Lực mạnh chỉ tác dụng trực tiếp lên các hạt cơ bản. Tuy thế, sự dư thừa hay rò rỉ của nó như quan sát các hadron (hay như lực liên kết các nucleon bao gồm proton và neutron trong hạt nhân) được coi như là lực hạt nhân. Ở đây lực mạnh tác dụng một cách gián tiếp, khi gluon truyền ra tạo thành các hạt ảo như meson pi và rho meson mà các nhà vật lý hạt nhân coi chúng là các hạt truyền của lực hạt nhân. Do không thể quan sát trực tiếp các hạt quark tự do cho nên ảnh hưởng của các hạt cơ bản là không quan sát trực tiếp được. Hiệu ứng này được gọi là sự giam hãm màu.
Lực hạt nhân yếu hay tương tác yếu có các hạt truyền là các boson W và Z có khối lượng lớn. Hiệu ứng quen thuộc nhất của lực này đó là phân rã beta (của các neutron trong hạt nhân) và đi kèm với sự phóng xạ. Thuật ngữ "yếu" xuất phát từ thực tế rằng cường độ của nó nhỏ hơn 1013 so với lực mạnh. Mặc dù vậy nó vẫn mạnh hơn lực hấp dẫn ở tầm tác dụng vi mô. Cả hai lực mạnh và lực yếu có tầm tác dụng ngắn trong cấp độ hạt nhân. Các nhà vật lý đã phát triển lý thuyết điện yếu với tiên đoán lực điện từ và lực yếu là không thể phân biệt được khi các hạt cơ bản trong trạng thái nhiệt độ xấp xỉ 1015 kelvin. Các nhiệt độ này đã được khảo sát trong các máy gia tốc hiện đại và chúng thể hiện những điều kiện sơ khai của vũ trụ trong những giây ngắn ngủi đầu tiên sau Vụ Nổ Lớn.
Các lực khác[sửa]
Một số lực là hệ quả của các lực cơ bản. Trong các tình huống như vậy, những mô hình lý tưởng có thể được sử dụng để hiểu rõ những quy luật vật lý.
Lực pháp tuyến[sửa]
- Xem chi tiết: Lực pháp tuyến
Lực pháp tuyến là do lực đẩy của tương tác giữa các nguyên tử tại bề mặt tiếp xúc. Khi các đám mây electron xếp đan xen nhau, nguyên lý loại trừ Pauli (do bản chất hạt fermion của electron) làm nảy sinh lực đẩy tác dụng theo hướng vuông góc với bề mặt tiếp xúc giữa hai vật.[14]Bản mẫu:Rp Ví dụ, lực pháp tuyến cản trở không cho chiếc bàn bị thụt xuống sàn nhà. Ngoài ra lực pháp tuyến xuất hiện khi có một lực tác động va vào một bề mặt không chuyển động được.[1][3]
Ma sát[sửa]
- Xem chi tiết: Ma sát
Ma sát là lực bề mặt chống lại xu hướng chuyển động tương đối giữa hai vị trí bề mặt. Lực ma sát tỷ lệ trực tiếp với lực pháp tuyến giữ cho hai vật rắn tách rời nhau ở những điểm tiếp xúc. Lực ma sát được phân loại thành hai loại lực: ma sát tĩnh và ma sát động.
Lực
ma
sát
tĩnh
(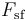 )
sẽ
bằng
và
ngược
hướng
với
lực
tác
dụng
song
song
với
bề
mặt
tiếp
xúc
cho
tới
một
giới
hạn
xác
định
bởi
hệ
số
ma
sát
tĩnh
(
)
sẽ
bằng
và
ngược
hướng
với
lực
tác
dụng
song
song
với
bề
mặt
tiếp
xúc
cho
tới
một
giới
hạn
xác
định
bởi
hệ
số
ma
sát
tĩnh
(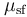 )
nhân
với
lực
pháp
tuyến
(
)
nhân
với
lực
pháp
tuyến
(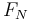 ).
Hay
nói
cách
khác
độ
lớn
của
ma
sát
tĩnh
thỏa
mãn
bất
đẳng
thức:
).
Hay
nói
cách
khác
độ
lớn
của
ma
sát
tĩnh
thỏa
mãn
bất
đẳng
thức:
-
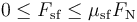 .
.
Ma
sát
động
(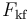 )
độc
lập
với
cả
lực
tác
dụng
và
sự
chuyển
động
của
vật.
Do
vậy
độ
lớn
của
lực
ma
sát
động
bằng:
)
độc
lập
với
cả
lực
tác
dụng
và
sự
chuyển
động
của
vật.
Do
vậy
độ
lớn
của
lực
ma
sát
động
bằng:
-
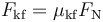 ,
,
với
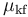 là
hệ
số
ma
sát
động.
Đối
với
hầu
hết
các
bề
mặt
tiếp
xúc,
hệ
số
ma
sát
động
nhỏ
hơn
hệ
số
ma
sát
tĩnh.
là
hệ
số
ma
sát
động.
Đối
với
hầu
hết
các
bề
mặt
tiếp
xúc,
hệ
số
ma
sát
động
nhỏ
hơn
hệ
số
ma
sát
tĩnh.
Sức căng[sửa]
- Xem chi tiết: Sức căng
Lực căng được mô hình hóa bằng những dây lý tưởng không có khối lượng, không gây ma sát, không thể phá vỡ được và không bị kéo giãn. Chúng có thể kết hợp với các ròng rọc lý tưởng cho phép các dây lý tưởng chuyển đổi hướng lực tác dụng. Các dây lý tưởng truyền lực căng một cách tức thời trong cặp tác dụng-phản tác dụng sao cho nếu hai vật nối với nhau bởi một dây lý tưởng, bất kỳ lực nào hướng dọc theo dây gây nên bởi vật thứ nhất được kết hợp với một lực hướng dọc theo dây theo hướng ngược lại gây bởi vật thứ hai.[35] Bằng cách nối những dây lý tưởng tương tự đối với cùng những vật như thế theo một cấu hình với các ròng rọc, lực căng của dây lên tải trọng có thể được tăng gấp bội cho phép ròng rọc có thể nâng được vật khối lượng lớn. Tuy nhiên, trong những cỗ máy đơn giản như ròng rọc, việc lợi về lực thì lại tương ứng với thiệt về quãng đường cần kéo dây để có thể di chuyển tải trọng. Quy luật này chính là hệ quả của định luật bảo toàn năng lượng do công tác dụng lên tải trọng là như nhau cho dù các cỗ máy có hoạt động theo cách nào đi chăng nữa.[1][3][36]
Lực đàn hồi[sửa]
- Xem chi tiết: Lực đàn hồi
Lực
đàn
hồi
tác
dụng
lên
lò
xo
khiến
nó
khôi
phục
lại
trạng
thái
ban
đầu.
Một
lò
xo
lý
tưởng
được
coi
là
không
có
khối
lượng,
không
có
ma
sát,
không
bị
đứt
gãy,
và
có
thể
dãn
vô
hạn.
Những
lò
xo
này
tác
dụng
lực
đẩy
khi
chúng
bị
nén
ngắn
lại,
hoặc
lực
kéo
khi
bị
kéo
dài,
lực
này
tỉ
lệ
với
độ
dịch
chuyển
của
lò
xo
từ
vị
trí
cân
bằng
của
nó.[37]
Robert
Hooke
đã
miêu
tả
mối
quan
hệ
tuyến
tính
này
vào
năm
1676
bởi
định
luật
mang
tên
ông
là
định
luật
Hooke.
Nếu
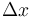 là
độ
dịch
chuyển,
lực
tác
dụng
bởi
lò
xo
lý
tưởng
sẽ
bằng:
là
độ
dịch
chuyển,
lực
tác
dụng
bởi
lò
xo
lý
tưởng
sẽ
bằng:
với
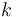 là
hằng
số
phụ
thuộc
vào
từng
loại
lò
xo.
Dấu
trừ
thể
hiện
cho
xu
hướng
của
lực
tác
dụng
theo
hướng
ngược
lại
khi
có
ngoại
lực
tác
dụng
lên
lò
xo.[1][3]
là
hằng
số
phụ
thuộc
vào
từng
loại
lò
xo.
Dấu
trừ
thể
hiện
cho
xu
hướng
của
lực
tác
dụng
theo
hướng
ngược
lại
khi
có
ngoại
lực
tác
dụng
lên
lò
xo.[1][3]
Cơ học môi trường liên tục[sửa]
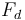 )
là
tổng
hợp
lực
của
sức
cản
không
khí
có
độ
lớn
bằng
trọng
lượng
của
vật
rơi
(
)
là
tổng
hợp
lực
của
sức
cản
không
khí
có
độ
lớn
bằng
trọng
lượng
của
vật
rơi
(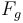 ),
lúc
này
vật
đạt
đến
trạng
thái
cân
bằng
động
hay
vận
tốc
cuối
cùng.
),
lúc
này
vật
đạt
đến
trạng
thái
cân
bằng
động
hay
vận
tốc
cuối
cùng.- Xem chi tiết: Áp suất
Cơ học và các định luật Newton lúc đầu được phát biểu trong trường hợp lực tác dụng lên các hạt điểm lý tưởng hơn là các vật thể hình học ba chiều. Tuy vậy trong thực tế, các lực tác dụng lên một vị trí của vật thể và có thể coi là ảnh hưởng đến những phần khác của vật. Trong trường hợp khi các dàn tinh thể nguyên tử trong một vật hành xử theo cách có thể chảy được, co lại, nở ra hoặc thay đổi hình dạng, lý thuyết cơ học môi trường liên tục miêu tả lực tác dụng lên vật thể và những hệ quả đối với cấu trúc bên trong của vật. Ví dụ, trong cơ học chất lỏng, sự chênh lệch áp suất hình thành lên lực theo hướng của gradient áp suất như sau:
với
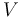 là
thể
tích
vật
chiếm
chỗ
trong
chất
lỏng
và
là
thể
tích
vật
chiếm
chỗ
trong
chất
lỏng
và
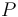 là
hàm
vô
hướng
miêu
tả
áp
suất
tại
mọi
vị
trí
trong
không
gian.
Gradient
áp
suất
và
sự
chênh
lệch
áp
suất
là
nguyên
nhân
của
lực
đẩy
nổi
đối
với
vật
trong
chất
lỏng
dưới
tác
dụng
của
trường
hấp
dẫn,
gió
trong
khoa
học
khí
quyển,
và
lực
nâng
trong
khí
động
lực
học
và
nghiên
cứu
chuyển
động
bay.[1][3]
là
hàm
vô
hướng
miêu
tả
áp
suất
tại
mọi
vị
trí
trong
không
gian.
Gradient
áp
suất
và
sự
chênh
lệch
áp
suất
là
nguyên
nhân
của
lực
đẩy
nổi
đối
với
vật
trong
chất
lỏng
dưới
tác
dụng
của
trường
hấp
dẫn,
gió
trong
khoa
học
khí
quyển,
và
lực
nâng
trong
khí
động
lực
học
và
nghiên
cứu
chuyển
động
bay.[1][3]
Một ví dụ cụ thể của những loại lực này là áp suất động lực của sức cản chất lỏng: một vật chuyển động trong môi trường chất lỏng bị một lực cản gây bởi tính nhớt của chất lỏng đó. Lực cản Stokes tỷ lệ xấp xỉ với vận tốc của vật và có hướng ngược lại:
với:
-
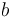 là
hằng
số
phụ
thuộc
vào
tính
chất
của
chất
lỏng
và
hình
học
của
vật
thể
(thường
là
tiết
diện
của
vật
thể),
và
là
hằng
số
phụ
thuộc
vào
tính
chất
của
chất
lỏng
và
hình
học
của
vật
thể
(thường
là
tiết
diện
của
vật
thể),
và -
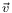 là
vận
tốc
của
vật.[1][3]
là
vận
tốc
của
vật.[1][3]
Một các trừu tượng hơn, lực trong cơ học môi trường liên tục được miêu tả đầy đủ bởi tenxơ ứng suất được định nghĩa là
với
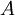 là
diện
tích
tiết
diện
tương
ứng
cho
thể
tích
mà
tenxơ
ứng
suất
đang
cần
tính.
Tenxơ
này
bao
gồm
thành
phần
áp
suất
gắn
liền
với
lực
tác
dụng
vuông
góc
với
mặt
cắt
tiết
diện
(ma
trận
chéo
của
tenxơ)
cũng
như
thành
phần
ứng
suất
cắt
gắn
liền
với
lực
tác
dụng
theo
hướng
song
song
với
mặt
cắt
tiết
diện
(các
thành
phần
không
thuộc
đường
chéo
của
biểu
diễn
ma
trận
tenxơ).
Tenxơ
ứng
suất
cũng
miêu
tả
các
lực
gây
ra
sự
biến
dạng
của
vật
thể
như
lực
nén
và
lực
kéo.[4][31]Bản
mẫu:Rp[38]Bản
mẫu:Rp
là
diện
tích
tiết
diện
tương
ứng
cho
thể
tích
mà
tenxơ
ứng
suất
đang
cần
tính.
Tenxơ
này
bao
gồm
thành
phần
áp
suất
gắn
liền
với
lực
tác
dụng
vuông
góc
với
mặt
cắt
tiết
diện
(ma
trận
chéo
của
tenxơ)
cũng
như
thành
phần
ứng
suất
cắt
gắn
liền
với
lực
tác
dụng
theo
hướng
song
song
với
mặt
cắt
tiết
diện
(các
thành
phần
không
thuộc
đường
chéo
của
biểu
diễn
ma
trận
tenxơ).
Tenxơ
ứng
suất
cũng
miêu
tả
các
lực
gây
ra
sự
biến
dạng
của
vật
thể
như
lực
nén
và
lực
kéo.[4][31]Bản
mẫu:Rp[38]Bản
mẫu:Rp
Giả lực[sửa]
- Xem chi tiết: Giả lực
Có những loại lực mà giá trị và hướng phụ thuộc vào hệ quy chiếu, có nghĩa là chúng xuất hiện khi sử dụng những hệ quy chiếu phi Newton (hay hệ quy chiếu phi quán tính). Những lực này bao gồm lực hướng tâm và lực Coriolis.[39] Những lực này được coi là giả lực do chúng không tồn tại trong hệ quy chiếu đang không bị gia tốc.[1][3]
Trong thuyết tương đối rộng, lực hấp dẫn trở thành giả lực khi nó xuất hiện trong những tình huống khi không thời gian được coi là không gian cong hơn là không gian phẳng.
Quay và xoắn[sửa]
- Xem chi tiết: Mô men lực
Lực
đi
kèm
với
mômen
lực
làm
quay
vật.
Về
mặt
toán
học
mô
men
lực
của
một
lực
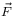 được
xác
định
đối
với
một
điểm
bất
kỳ
thông
qua
tích
có
hướng:
được
xác
định
đối
với
một
điểm
bất
kỳ
thông
qua
tích
có
hướng:
với
-
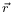 là
vec
tơ
vị
trí
lực
đặt
vào
so
với
điểm
quy
chiếu.
là
vec
tơ
vị
trí
lực
đặt
vào
so
với
điểm
quy
chiếu.
Ngẫu lực là sự quay tương đương của lực theo cùng cách mà vec tơ vị trí quay một góc tương đương, hoặc vec tơ vận tốc góc cho vận tốc và mô men động lượng cho động lượng. Theo hệ quả của Định luật thứ nhất Newton, tồn tại quán tính quay để đảm bảo mọi vật sẽ vẫn duy trì mô men động lượng của nó trừ khi có ngẫu lực không cân bằng tác động lên. Tương tự, Định luật thứ hai Newton được dùng để suy ra phương trình cho gia tốc góc tức thời của vật rắn:
với
-
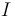 là
mô
men
quán
tính
của
vật
là
mô
men
quán
tính
của
vật -
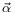 là
gia
tốc
góc.
là
gia
tốc
góc.
Công thức này cũng dùng để định nghĩa cho khái niệm mô men quán tính. Trong cơ học cao cấp, nơi miêu tả sự quay theo khoảng thời gian, mô men quán tính được thay bằng khái niệm tổng quát hơn là tensơ mô men quán tính, cho phéo khi phân tích đầy đủ và chi tiết đặc tính của vật quay bao gồm tiến động và chương động.
Một cách tương đương, dạng vi phân của Định luật thứ hai Newton đưa ra định nghĩa khác về mô men lực:
-
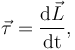 [40]
với
[40]
với
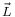 là
động
lượng
góc
của
hạt.
là
động
lượng
góc
của
hạt.
Định luật thứ ba Newton nói rằng mọi vật tác động ngẫu lực thì chính chúng sẽ chịu một ngẫu lực bằng về độ lớn nhưng ngược hướng,[41] và do vậy hàm ý trực tiếp định luật bảo toàn mô men động lượng cho hệ kín chịu sự quay thông qua tác dụng của nội mô men xoắn.
Lực hướng tâm[sửa]
- Xem chi tiết: Lực hướng tâm
Một vật chuyển động gia tốc trên quỹ đạo tròn, nó chịu một lực có độ lớn bằng:[42]
với
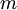 là
khối
lượng
của
vật,
là
khối
lượng
của
vật,
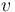 là
vận
tốc
và
là
vận
tốc
và
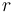 là
độ
lớn
khoảng
cách
đến
tâm
của
quỹ
đạo
tròn
và
là
độ
lớn
khoảng
cách
đến
tâm
của
quỹ
đạo
tròn
và
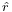 là
vectơ
đơn
vị
chỉ
theo
hướng
từ
tâm
ra
ngoài.
Lực
hướng
tâm
luôn
hướng
về
tâm
của
đường
tròn
tiếp
xúc
với
quỹ
đạo
của
vật
thể
tại
một
thời
điểm.
Lực
này
tác
dụng
vuông
góc
với
vectơ
vận
tốc
của
vật
và
do
vậy
không
làm
thay
đổi
độ
lớn
vận
tốc
của
nó,
nhưng
chỉ
làm
thay
đổi
hướng
của
vectơ
vận
tốc.
Lực
gây
ra
chuyển
động
của
vật
có
thể
phân
tích
thành
một
thành
phần
vuông
góc
với
quỹ
đạo
của
nó,
và
một
thành
phần
tiếp
tuyến
với
quỹ
đạo.
Thành
phần
tiếp
tuyến
làm
tăng
tốc
hoặc
làm
chậm
vật
trong
khi
thành
phần
vuông
góc
(lực
hướng
tâm)
làm
thay
đổi
hướng
của
nó.[1][3]
là
vectơ
đơn
vị
chỉ
theo
hướng
từ
tâm
ra
ngoài.
Lực
hướng
tâm
luôn
hướng
về
tâm
của
đường
tròn
tiếp
xúc
với
quỹ
đạo
của
vật
thể
tại
một
thời
điểm.
Lực
này
tác
dụng
vuông
góc
với
vectơ
vận
tốc
của
vật
và
do
vậy
không
làm
thay
đổi
độ
lớn
vận
tốc
của
nó,
nhưng
chỉ
làm
thay
đổi
hướng
của
vectơ
vận
tốc.
Lực
gây
ra
chuyển
động
của
vật
có
thể
phân
tích
thành
một
thành
phần
vuông
góc
với
quỹ
đạo
của
nó,
và
một
thành
phần
tiếp
tuyến
với
quỹ
đạo.
Thành
phần
tiếp
tuyến
làm
tăng
tốc
hoặc
làm
chậm
vật
trong
khi
thành
phần
vuông
góc
(lực
hướng
tâm)
làm
thay
đổi
hướng
của
nó.[1][3]
Tích phân động học[sửa]
- Xem chi tiết: Xung lực
Lực có thể dùng để định nghĩa một số khái niệm vật lý bằng cách tích phân nó theo các biến động học. Ví dụ, tích phân theo thời gian sẽ cho định nghĩa của xung lực:[43]
mà theo định luật hai của Newton nó phải tương đương với sự thay đổi của động lượng (định lý xung lượng- động lượng).
Tương tự, tích phân lực theo vị trí cho định nghĩa của công cơ học tác dụng bởi lực:[1]Bản mẫu:Rp
và nó tương đương với sự thay đổi của động năng (định lý công năng lượng).[1]Bản mẫu:Rp
Công
suất
P
là
tỷ
lệ
thay
đổi
dW/dt
của
W
theo
thời
gian,
khi
quỹ
đạo
được
mở
rộng
bởi
sự
thay
đổi
vị
trí
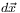 trong
khoảng
thời
gian
dt:[1]Bản
mẫu:Rp
trong
khoảng
thời
gian
dt:[1]Bản
mẫu:Rp
với
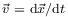 là
vận
tốc.
là
vận
tốc.
Thế năng[sửa]
- Xem chi tiết: Thế năng
Một
khái
niệm
toán
học
hữu
ích
thay
thế
cho
lực
trong
nhiều
trường
hợp
đó
là
thế
năng.
Ví
dụ
lực
hấp
dẫn
tác
dụng
lên
một
vật
có
thể
coi
như
là
tác
dụng
của
trường
hấp
dẫn
có
mặt
tại
vị
trí
của
vật.
Bằng
cách
viết
lại
định
nghĩa
của
năng
lượng
(thông
qua
định
nghĩa
của
công
cơ
học),
trường
vô
hướng
thế
năng
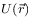 được
định
nghĩa
là
trường
mà
gradien
có
độ
lớn
bằng
và
ngược
hướng
với
lực
tác
dụng
tại
mỗi
điểm:
được
định
nghĩa
là
trường
mà
gradien
có
độ
lớn
bằng
và
ngược
hướng
với
lực
tác
dụng
tại
mỗi
điểm:
Lực có thể được phân loại thành lực bảo toàn hoặc lực không bảo toàn. Lực bảo toàn là tương đương với gradien của trường thế năng trong khi lực không bảo toàn thì không có tính chất này.[1][3]
Lực bảo toàn[sửa]
- Xem chi tiết: Lực bảo toàn
Lực bảo toàn tác động lên một hệ kín gắn liền với công cơ học cho phép năng lượng được biến đổi giữa các dạng động năng và thế năng. Điều này có nghĩa là trong một hệ kín cơ năng được bảo toàn bất cứ khi nào có lực bảo toàn tác động lên hệ. Do vậy lực liên hệ trực tiếp với hiệu thế năng giữa hai vị trí khác nhau trong không gian,[44] và có thể coi như một trường thế năng giả theo cùng cách với hướng và lưu lượng nước trong biểu đồ đường đồng mức của địa hình.[1][3]
Các
lực
bảo
toàn
bao
gồm
lực
hấp
dẫn,
lực
điện
từ
và
lực
đàn
hồi
lò
xo.
Mỗi
lực
này
được
mô
hình
hóa
mà
phụ
thuộc
vào
vectơ
vị
trí
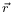 hướng
từ
trường
thế
năng
đối
xứng
cầu
ra
ngoài.[45]
Xét
ví
dụ
dưới:
hướng
từ
trường
thế
năng
đối
xứng
cầu
ra
ngoài.[45]
Xét
ví
dụ
dưới:
Đối với lực hấp dẫn:
với
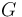 là
hằng
số
hấp
dẫn,
và
là
hằng
số
hấp
dẫn,
và
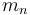 là
khối
lượng
của
vật
n.
là
khối
lượng
của
vật
n.
Đối với lực tĩnh điện:
với
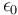 là
hằng
số
điện
môi,
và
là
hằng
số
điện
môi,
và
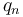 là
điện
tích
của
vật
n.
là
điện
tích
của
vật
n.
Đối với lực lò xo:
với
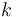 là
hằng
số
đàn
hồi
của
lò
xo.[1][3]
là
hằng
số
đàn
hồi
của
lò
xo.[1][3]
Lực không bảo toàn[sửa]
Trong một số mô hình vật lý nhất định, khó có thể định nghĩa lực dựa trên khái niệm gradien của thế năng. Điều này thường do những giả sử vĩ mô cho phép thu được lực từ mức độ trung bình thống kê vĩ mô của những hệ có trạng thái vi mô. Ví dụ, ma sát có nguyên nhân từ gradien của rất nhiều thế năng tĩnh điện giữa các nguyên tử, nhưng nó lại thể hiện ra như một lực độc lập với bất kỳ vectơ vị trí vĩ mô nào. Lực không bảo toàn ngoài lực ma sát ra bao gồm lực tiếp xúc, sức căng bề mặt, sự nén và kéo. Tuy nhiên, cho những tình huống miêu tả thích hợp, tất cả những lực trên là kết quả của lực bảo toàn do mỗi lực vĩ mô này là tổng hợp của các gradien thế năng vi mô.[1][3]
Mối liên hệ giữa lực không bảo toàn vĩ mô với lực bảo toàn vi mô được miêu tả chi tiết trong cơ học thống kê. Trong hệ kín vĩ mô, lực không bảo toàn tác động đến sự thay đổi nội năng của hệ và thường đi kèm với hiệu ứng truyền nhiệt. Theo định luật thứ hai của nhiệt động lực học, lực không bảo toàn là kết quả cần thiết của quá trình biến đổi năng lượng trong hệ kín từ trạng thái trật tự chuyển sang trạng thái ngẫu nhiên khi entropy của hệ tăng lên.[1][3]
Đơn vị đo của lực[sửa]
Đơn vị SI của lực là newton (ký hiệu N), là lực cần thiết để làm một vật có khối lượng một kilogram thu gia tốc một mét trên giây bình phương, hoặc kg·m·s−2.[46] Tương ứng, đơn vị của lực theo hệ CGS là dyne, là lực cần thiết để làm một vật có khối lượng một gram thu gia tốc một centimet trên giây bình phương, hayg·cm·s−2. Một newton bằng 100,000 dyne.
Theo hệ đơn vị Anh FPS, thì đơn vị của lực là pound-lực (lbf), được định nghĩa là lực hấp dẫn tác dụng lên một khối lượng một pound trong một trọng trường tiêu chuẩn 9.80665 m·s−2.[46] Đơn vị pound-lực đưa ra một đơn vị khác cho khối lượng: một slug là khối lượng mà sẽ thu được gia tốc một foot trên giây bình phương khi bị tác động bởi một lực một pound-lực.[46]
Một đơn vị khác của lực theo hệ FPS tuyệt đối là poundal, được định nghĩa là lực cần thiết để gia tốc cho khối lượng một pound đạt một foot trên giây bình phương.[46] Các đơn vị slug và poundal được đưa ra nhằm tránh hằng số tỷ lệ trong định luật 2 Newton.
Pound-lực cũng có một đơn vị tương ứng trong hệ đo lường mét nhưng ít được sử dụng hơn newton: đó là kilogram-lực (kgf) (đôi khi gọi là kilopond), là lực tác động lên một khối lượng một kilogram gây ra bởi một trọng trường tiêu chuẩn.[46] Kilogram-lực dẫn đến một đơn vị đo khối lượng khác, nhưng ít khi sử dụng đó là:metric slug (đôi khi gọi là mug hay hyl) là khối lượng mà thu được một gia tốc 1 m·s−2 khi bị tác dụng một lực 1 kgf. Kilogram-lực không thuộc hệ đo lường quốc tế hiện đại, và thường bị phản đối; tuy nhiên nó vẫn còn được dùng cho một vài trường hợp chẳng hạn như biểu diễn phản lực, lực kéo của nan hoa xe đạp, mô men xoắn của bộ chìa vặn đai ốc và mô men xoắn công suất động cơ. Những đơn vị của lực ít được dùng đến như sthène tương đương với 1000 N và kip tương đương với 1000 lbf.
Danh sách các loại lực[sửa]
- Trọng lực
- Phản lực
- Áp lực
- Lực ma sát
- Lực đàn hồi
- Lực động
- Lực hướng tâm
- Lực ly tâm
- Lực Culomb (hay lực tĩnh điện)
- Lực Ampere (hay lực điện động)
- Lực Lorentz
- Lực Faraday (hay lực điện từ)
Ghi chú[sửa]
- ↑ Trong cuốn Principia Mathematica Newton sử dụng dạng phương trình cho xung lực. Xem Xung lực.
- ↑ "Chú ý quan trọng ở đây là chúng ta không thể dẫn ra biểu thức tổng quát cho định luật hai Newton đối với hệ có khối lượng thay đổi bằng cách coi khối lượng trong phương trình F = dP/dt = d(Mv) như là một biến số. [...] Chúng ta có thể sử dụng F = dP/dt nhằm phân tích hệ có khối lượng thay đổi chỉ khi chúng ta áp dụng nó cho một hệ toàn thể với khối lượng không đổi với các phần trong nó có thể trao đổi khối lượng cho nhau." [Trích nguyên văn] Bản mẫu:Harv
- ↑ "Bất kỳ một lực đơn lẻ nào chỉ là một khía cạnh của tương tác qua lại giữa hai vật." Bản mẫu:Harv
- ↑ Xem Cơ học lượng tử – Tham khảo
Tham khảo[sửa]
- ↑ 1,00 1,01 1,02 1,03 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 Feynman, Richard P. (2010). The Feynman lectures on physics. (ấn bản New millennium). New York: BasicBooks. ISBN 9780465024933.
- ↑ “glossary”. Earth Observatory. NASA. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.. trích dẫn: Force: Any external agent that causes a change in the motion of a free body, or that causes stress in a fixed body.
- ↑ 3,00 3,01 3,02 3,03 3,04 3,05 3,06 3,07 3,08 3,09 3,10 3,11 3,12 3,13 3,14 3,15 3,16 3,17 3,18 3,19 3,20 3,21 3,22 3,23 3,24 Kleppner, Daniel; Robert Kolenkow (1973). An Introduction to Mechanics. McGraw-Hill. ISBN 0-07-035048-5.
- ↑ 4,0 4,1 4,2 4,3 4,4 4,5 4,6 4,7 4,8 University Physics, Sears, Young & Zemansky, pp.18–38
- ↑ Heath, T.L.. “The Works of Archimedes (1897). The unabridged work in PDF form (19 MB)”. Archive.org. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ 6,0 6,1 6,2 Weinberg, S. (1994). Dreams of a Final Theory. Vintage Books USA. ISBN 0-679-74408-8.
- ↑ 7,0 7,1 7,2 7,3 7,4 7,5 Newton, Isaac (1999). The Principia Mathematical Principles of Natural Philosophy. Berkeley: University of California Press. ISBN 0-520-08817-4. This is a recent translation into English by I. Bernard Cohen and Anne Whitman, with help from Julia Budenz.
- ↑ DiSalle, Robert (Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.). “Space and Time: Inertial Frames”. Stanford Encyclopedia of Philosophy. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Ngoại trừ một quy tắc là: Landau, L. D.; Akhiezer, A. I.; Lifshitz, A. M. (196). General Physics; mechanics and molecular physics (ấn bản First English). Oxford: Pergamon Press. ISBN 0-08-003304-0. Translated by: J. B. Sykes, A. D. Petford, and C. L. Petford. Library of Congress Catalog Number 67-30260. Trong phần 7, trang 12–14, cuốn sách định nghĩa lực bằng dp/dt.
- ↑ Jammer, Max (1999). Concepts of force: a study in the foundations of dynamics (ấn bản Facsim.). Mineola, N.Y.: Dover Publications. 220–222. ISBN 9780486406893.
- ↑ Noll, Walter (Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.). “On the Concept of Force” định dạng (pdf). Carnegie Mellon University. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ C. Hellingman (1992). "Newton's third law revisited". Phys. Educ. 27 (2): 112–115. doi:. Bibcode: 1992PhyEd..27..112H. "Trích dẫn lời Newton trong cuốn Principia: Không chỉ Mặt Trời hút Sao Mộc, hay Sao Mộc hút Mặt Trời; mà đó là một tác dụng trong đó Mặt Trời và Sao Mộc dần dần trở lên gần nhau hơn.".
- ↑ Dr. Nikitin (2007). “Dynamics of translational motion”. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ 14,0 14,1 14,2 14,3 14,4 Cutnell & Johnson 2003
- ↑ “Seminar: Visualizing Special Relativity”. The Relativistic Raytracer. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Susskind, Leonard. “Relativistic Lorentz force”. Lecture notes. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ “Introduction to Free Body Diagrams”. Physics Tutorial Menu. University of Guelph. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Henderson, Tom (2004). “The Physics Classroom”. The Physics Classroom and Mathsoft Engineering & Education, Inc.. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ “Static Equilibrium”. Physics Static Equilibrium (forces and torques). University of the Virgin Islands. Bản chính lưu trữ Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Drake, Stillman (1978). Galileo At Work. Chicago: University of Chicago Press. ISBN 0-226-16226-5
- ↑ 21,0 21,1 Shifman, Mikhail (1999). ITEP lectures on particle physics and field theory. World Scientific. ISBN 981-02-2639-X.
- ↑ Nave, Carl Rod. “Pauli Exclusion Principle”. HyperPhysics. University of Guelph. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ “Fermions & Bosons”. The Particle Adventure. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Cook, A. H. (1965). "A New Absolute Determination of the Acceleration due to Gravity at the National Physical Laboratory". Nature 208 (5007): 279. doi:. Bibcode: 1965Natur.208..279C. http://www.nature.com/nature/journal/v208/n5007/abs/208279a0.html. Truy cập ngày 4 tháng 1 năm 2008.
- ↑ 25,0 25,1 University Physics, Sears, Young & Zemansky, pp59–82
- ↑ “Sir Isaac Newton: The Universal Law of Gravitation”. Astronomy 161 The Solar System. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Watkins, Thayer. “Perturbation Analysis, Regular and Singular”. Department of Economics. San José State University.
- ↑ Kollerstrom, Nick (2001). “Neptune's Discovery. The British Case for Co-Prediction.”. University College London. Bản chính lưu trữ Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Einstein, Albert (1916). "The Foundation of the General Theory of Relativity" (PDF). Annalen der Physik 49 (7): 769–822. doi:. Bibcode: 1916AnP...354..769E. http://www.alberteinstein.info/gallery/gtext3.html. Truy cập ngày 3 tháng 9 năm 2006.
- ↑ Coulomb, Charles (1784). "Recherches théoriques et expérimentales sur la force de torsion et sur l'élasticité des fils de metal". Histoire de l'Académie Royale des Sciences: 229–269.
- ↑ 31,0 31,1 31,2 Feynman volume 2
- ↑ Scharf, Toralf (2007). Polarized light in liquid crystals and polymers. John Wiley and Sons. tr. 19. ISBN 0-471-74064-0. http://books.google.com/?id=CQNE13opFucC., Chapter 2, p. 19
- ↑ Duffin, William (1980). Electricity and Magnetism, 3rd Ed.. McGraw-Hill. 364–383. ISBN 0-07-084111-X.
- ↑ Stevens, Tab (Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.). “Quantum-Chromodynamics: A Definition – Science Articles”. Bản chính lưu trữ Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ “Tension Force”. Non-Calculus Based Physics I. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Fitzpatrick, Richard (Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.). “Strings, pulleys, and inclines”. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Nave, Carl Rod. “Elasticity”. HyperPhysics. University of Guelph. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Kleppner & Kolenkow 2010
- ↑ Mallette, Vincent (Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.). “Inwit Publishing, Inc. and Inwit, LLC – Writings, Links and Software Distributions – The Coriolis Force”. Publications in Science and Mathematics, Computing and the Humanities. Inwit Publishing, Inc.. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Nave, Carl Rod. “Newton's 2nd Law: Rotation”. HyperPhysics. University of Guelph. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Fitzpatrick, Richard (Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.). “Newton's third law of motion”. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Nave, Carl Rod. “Centripetal Force”. HyperPhysics. University of Guelph. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Hibbeler, Russell C. (2010). Engineering Mechanics, 12th edition. Pearson Prentice Hall. tr. 222. ISBN 0-13-607791-9
- ↑ Singh, Sunil Kumar (Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định.). “Conservative force”. Connexions. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ Davis, Doug. “Conservation of Energy”. General physics. Truy cập Lỗi khi kêu gọi {{Chú thích web}}: hai tham số url và title phải được chỉ định..
- ↑ 46,0 46,1 46,2 46,3 46,4 Wandmacher, Cornelius; Johnson, Arnold (1995). Metric Units in Engineering. ASCE Publications. tr. 15. ISBN 0-7844-0070-9.
Đọc thêm[sửa]
- Các lực trong tự nhiên. V. Grigoriev, G. Miakisev; Ngô Đặng Nhân dịch - Tái bản lần 1. Nhà xuất bản Khoa học và Kỹ thuật, 2002, 527tr
- Tiếng Anh
- Corben, H.C.; Philip Stehle (1994). Classical Mechanics. New York: Dover publications. 28–31. ISBN 0-486-68063-0.
- Cutnell, John D.; Johnson, Kenneth W. (2003). Physics, Sixth Edition. Hoboken, NJ: John Wiley & Sons Inc.. ISBN 0471151831.
- Feynman, Richard P.; Leighton; Sands, Matthew (2010). The Feynman lectures on physics. Vol. I: Mainly mechanics, radiation and heat (ấn bản New millennium). New York: BasicBooks. ISBN 978-0465024933.
- Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2010). The Feynman lectures on physics. Vol. II: Mainly electromagnetism and matter (ấn bản New millennium). New York: BasicBooks. ISBN 978-0465024940.
- Halliday, David; Resnick, Robert; Krane, Kenneth S. (2001). Physics v. 1. New York: John Wiley & Sons. ISBN 0-471-32057-9.
- Kleppner, Daniel; Kolenkow, Robert J. (2010). An introduction to mechanics (ấn bản 3. print). Cambridge: Cambridge University Press. ISBN 0521198216.
- Bản mẫu:Cite encyclopedia
- Sears F., Zemansky M. & Young H. (1982). University Physics. Reading, MA: Addison-Wesley. ISBN 0-201-07199-1.
- Serway, Raymond A. (2003). Physics for Scientists and Engineers. Philadelphia: Saunders College Publishing. ISBN 0-534-40842-7.
- Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (ấn bản 5th). W. H. Freeman. ISBN 0-7167-0809-4.
- Verma, H.C. (2004). Concepts of Physics Vol 1. (ấn bản 2004 Reprint). Bharti Bhavan. ISBN 8177091875.
Liên kết ngoài[sửa]
- Video lecture on Newton's three laws by Walter Lewin from MIT OpenCourseWare
- A Java simulation on vector addition of forces
- Force Unit Converter
Liên kết đến đây
- Xem thêm liên kết đến trang này.