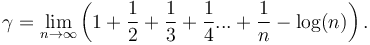Leonhard Euler
Leonhard Euler (đọc là "Ơ-le" theo phiên âm từ tiếng Pháp hay chính xác hơn là "Ôi-lờ" [ˈɔʏlɐ] theo phiên âm tiếng Đức; 15 tháng 4, 1707 – 18 tháng 9, 1783) là một nhà toán học và nhà vật lý học Thụy Sĩ. Ông (cùng với Archimedes và Newton) được xem là một trong những nhà toán học lừng lẫy nhất. Ông là người đầu tiên sử dụng từ "hàm số" (được Gottfried Leibniz định nghĩa trong năm 1694) để miêu tả một biểu thức có chứa các đối số, như y = f(x). Ông cũng được xem là người đầu tiên dùng vi tích phân trong môn vật lý.
Ông sinh và lớn lên tại Basel, và được xem là thần đồng toán học từ thuở nhỏ. Ông làm giáo sư toán học tại Sankt-Peterburg, sau đó tại Berlin, rồi trở lại Sankt-Peterburg. Ông là nhà toán học viết nhiều nhất: tất cả các tài liệu ông viết chứa đầy 75 tập. Ông là nhà toán học quan trọng nhất trong thế kỷ 18 và đã suy ra nhiều kết quả cho môn vi tích phân mới được thành lập. Ông bị mù hoàn toàn trong 17 năm cuối cuộc đời, nhưng khoảng thời gian đó là lúc ông cho ra hơn nửa số bài ông viết.
Tên của ông đã được đặt cho một miệng núi lửa trên Mặt Trăng và cho tiểu hành tinh 2002 Euler.
Mục lục
Tiểu sử[sửa]
Leonhard Euler sinh ngày 15 tháng 4 năm 1707, là con của một mục sư tại Basel, Thụy Sĩ. Lúc còn nhỏ, ông đã tỏ ra có tài năng trong môn toán học, nhưng cha ông muốn ông học giáo lý và trở thành một mục sư. Năm 1720 Euler bắt đầu học tại Đại học Basel. Tại đây ông được quen với Daniel và Nikolaus Bernoulli, và họ đã nhận thấy tài năng toán học của ông. Cha của ông, Paul Euler, đã tham dự một vài bài thuyết giảng toán học của Jakob Bernoulli và kính trọng gia đình ông. Khi Daniel và Nikolaus xin ông cho con ông học môn toán ông bằng lòng và Euler bắt đầu học toán.
Vào năm 1727 Euler được nữ hoàng Nga Ekaterina I mời đến Sankt-Peterburg. Ông trở thành giáo sư vật lý học năm 1730, và cũng dạy toán năm 1733. Euler là người đầu tiên xuất bản một cuốn sách dạy cơ học có phương pháp trong năm 1736: Mechanica sive motus scientia analytice exposita (Chuyển động cơ học được giải thích bởi ngành giải tích). Vì ông quan sát mặt trời nhiều quá, đến năm 1735 mắt phải ông đã bị mù một phần.
Năm 1733 ông kết hôn với Ekaterina (Katharina) Gsell, con gái của giám đốc Viện hàn lâm nghệ thuật. Họ có 13 con, nhưng chỉ có ba người con trai và hai người con gái sống sót. Con cháu của họ giữ những vị trí quan trọng tại Nga trong thế kỷ 19.
Vào năm 1741, nhằm thu hút nhân tài về phục vụ đất nước, vị tân vương nước Phổ là Friedrich II Đại Đế xuống Thánh chỉ vời Euler đến làm Viện trưởng Viện toán tại Viện Hàn lâm Khoa học Vương quốc Phổ trên đất kinh kỳ Berlin.[1] Ông viết rất nhiều trong thời gian ở kinh đô Berlin, nhưng ông không có được địa vị tốt vì nhà vua bất hòa với ông. Vì thế, ông trở về Sankt-Peterburg năm 1766, lúc đó dưới triều Ekaterina II, và sống ở đó cho đến khi mất.
Tuy bị mù hoàn toàn, ông vẫn viết được vì ông có trí nhớ siêu thường và có thể dùng óc để tính toán được. Có chuyện kể rằng có khi ông và người phụ tá của ông tính kết quả của một dãy số với 17 con số và nhận biết được là đáp số của ông và của người phụ tá khác nhau trong con số thứ 50. Khi họ tính lại thì thấy rằng ông đã tính đúng!
Người ta ước tính rằng, phải làm việc 8 giờ một ngày trong suốt 50 năm để có thể ghi chép bằng tay tất cả những công trình của ông. Phải đợi đến năm 1910, mới có một bộ sưu tập, tụ hợp tất cả các công trình này một cách đầy đủ, và nó được chứa trong 70 tập sách. Theo lời kể của Adrien-Marie Legendre, Euler thường hoàn thành một bài chứng minh trong khoảng thời gian gọi dùng cơm tối của mình.
Euler
là
một
người
rất
sùng
đạo.
Có
một
giai
thoại
phổ
biến
nói
rằng
Euler
đã
thách
đố
Denis
Diderot
tại
cung
điện
của
Ekaterina
Đại
đế,
"Thưa
ngài,
cách
suy
luận
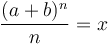 do
đó
Thượng
đế
tồn
tại";
tuy
nhiên
giai
thoại
này
là
sai.
do
đó
Thượng
đế
tồn
tại";
tuy
nhiên
giai
thoại
này
là
sai.
Khi Euler mất, nhà toán học và triết học Hầu tước de Condorcet bình luận "... et il cessa de calculer et de vivre" (và ông ấy đã ngừng tính và ngừng sống).
Các khám phá[sửa]
Euler cùng với Daniel Bernoulli đã hoàn thành định luật, ở đó phát biểu rằng lực xoắn trên một sợi dây chun mỏng tỉ lệ với độ đàn hồi của vật liệu và mô men quán tính của mặt cắt. Ông đồng thời cũng đưa ra phương trình Euler, một tập hợp các định luật chuyển động trong thủy động lực học, quan hệ trực tiếp với định luật chuyển động của Newton. Những phương trình này có dạng tương đương với các phương trình Navier-Stokes với độ nhớt bằng 0. Đó là một điều thú vị bởi chúng là nguyên nhân dẫn đến sự tồn tại của các sóng sốc.
Ông còn có đóng góp to lớn cho thuyết phương trình vi phân. Cụ thể, ông được biết đến nhiều với việc sáng tạo ra một chuỗi các phương pháp tính xấp xỉ, được sử dụng nhiều trong tinh toán. Và phương pháp nổi tiếng nhất trong đó chính là phương pháp Euler.
Trong
lý
thuyết
số
ông
đã
sáng
tạo
ta
hàm
totient.
Totient
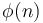 của
một
số
nguyên
dương
n
được
định
nghĩa
là
số
các
số
nguyên
dương
nhỏ
hơn
hoặc
bằng
n
và
nguyên
tố
cùng
nhau
với
n.
Ví
dụ
của
một
số
nguyên
dương
n
được
định
nghĩa
là
số
các
số
nguyên
dương
nhỏ
hơn
hoặc
bằng
n
và
nguyên
tố
cùng
nhau
với
n.
Ví
dụ
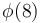 là
4
số
1,
3,
5,
7
đều
là
số
nguyên
tố
nhỏ
hơn
8.
là
4
số
1,
3,
5,
7
đều
là
số
nguyên
tố
nhỏ
hơn
8.
Trong ngành giải tích, Euler đã tổng hợp hóa tích phân Leibniz với phương pháp tính Newton thành một dạng, gọi là vi phân.
Ông hoàn thành nền móng vào năm 1735 bằng việc giải quyết bài toán Basel, vấn đề đã tồn tại trong một thời gian dài.[2]
-
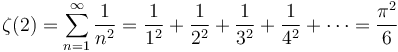 ,
,
ở
đó
 là
hàm
Euler
zeta
(không
nên
lầm
lẫn
với
hàm
Riemann
zeta
vốn
không
hoàn
toàn
giống
nhau
ở
miền
giá
trị
của
x).
là
hàm
Euler
zeta
(không
nên
lầm
lẫn
với
hàm
Riemann
zeta
vốn
không
hoàn
toàn
giống
nhau
ở
miền
giá
trị
của
x).
Ông
còn
đưa
ra
một
biểu
thức
nổi
tiếng
trong
toán
học,
là
sợi
dây
liên
hệ
giữa
hàm
số
mũ
phức
và
hàm
số
lượng
giác,
hay
còn
gọi
là
đồng
nhất
thức
Euler:
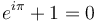 hay
hay
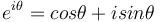
Năm 1735, ông tìm ra hằng số Euler-Mascheroni, được sử dụng rất nhiều trong các phương trình vi phân.
Ông là người cùng khám phá ra công thức Euler-Maclaurin, là một công cụ rất quan trọng trong việc tính toán các tích phân phức tạp, các tổng và chuỗi khó.
Trong hình học và topo đại số có một sợi dây liên kết chính là công thức Euler, ở đó liên hệ giữa các cạnh, đỉnh và mặt của một đa diện. Công thức tổng quát đó là: F - E + V = 2, ở đó F là số mặt, E là số cạnh và V là số đỉnh. Định lý này được áp dụng cho mọi đa diện lồi. Với các đồ thị không phẳng, có một biểu thức tổng quát. Nếu đồ thị có thể được nhúng vào trong một đa tạp M, thì F - E + V = X(M), ở đó X là Đặc trưng Euler của đa tạp, một hằng số ở đó là bất biến với mọi biến dạng liên tục. Đặc trưng Euler của một đa tạp liên thông đơn giản là một hình cầu và một mặt phẳng là 2. Công thức tổng quát với một đồ thị phẳng là: F - E + V - C = 1, ở đó C số thành phần liên thông của đồ thị.
Năm 1736, Euler giải được bài toán nổi tiếng 7 chiếc cầu Königsberg, chính xác hơn, ông chứng minh bài toán không có đáp số. Kết quả được công bố trên bài báo nhan đề Solutio problematis ad geometriam situs pertinentis, và đó chính là ứng dụng sớm nhất của lý thuyết đồ thị hay của topo học.
Tác phẩm nổi tiếng[sửa]
Euler có khối lượng sách viết đồ sộ nhưng những cuốn sách nổi tiếng nhất của ông bao gồm:
- Elements of Algebra (Nhập môn Đại số học). Cuốn sách về đại số căn bản này bắt đầu bàn một lời bàn luận về bản chất các con số và một lời giới thiệu tổng quan về đại số, bao gồm các công thức dành cho cách giải phương trình đa thức.
- Introductio in analysin infinitorum (1748): Nhập môn về giải tích vô cùng bé.
- Hai cuốn sách có ảnh hưởng về vi tích phân: Institutiones calculi differentialis Phép tính vi phân (1755) và Institutiones calculi integralis Phép tính tích phân (1768–1770).
- Principia motus fluidorum (1761): Nguyên lý chuyển động của chất lưu; cuốn sách trình bày phương trình liên tục và phương trình Euler.
- Lettres à une Princesse d'Allemagne (Lá thư gửi một Quận chúa Đức) (1768–1772). Có trực tuyến (bằng tiếng Pháp). Bản dịch tiếng Anh, có ghi chú, và cuộc đời của Euler có trực tuyến tại Google Books: Tập 1, Tập 2
- Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimetrici latissimo sensu accepti (1744). Tựa đề Latin dịch là Phương pháp tìm những đường cong có tính chất cực đại hoặc cực tiểu, hoặc lời giải cho bài toán đẳng cấu trong chừng mực chấp nhận rộng rãi nhất.[3]
Trích dẫn[sửa]
- "Lisez Euler, lisez Euler, c'est notre maître à tous." (Hãy đọc Euler, ông ấy là bậc thầy trong mọi lĩnh vực.) —Pierre-Simon Laplace
Chú thích[sửa]
- ↑ David Fraser, Frederick the Great: King of Prussia, trang 241
- ↑ Wanner, Gerhard; Harrier, Ernst (March 2005). Analysis by its history (ấn bản 1st). Springer. tr. 62.
- ↑ E65 — Methodus… entry at Euler Archives
Tham khảo[sửa]
- Euler, Leonhard (1748). Introductio in analysin infinitorum. English translation Introduction to Analysis of the Infinite by John Blanton (Book I, ISBN 0-387-96824-5, Springer-Verlag 1988; Book II, ISBN 0-387-97132-7, Springer-Verlag 1989).
- Euler Leonhardt: Lettres à une Princesse d'Allemagne; at http://www.bookmine.org
- Dunham, William (1999). Euler: The Master of Us All, Washington: Mathematical Association of America. ISBN 0-88385-328-0.
- Heimpell, Hermann, Theodor Heuss, Benno Reifenberg (editors). 1956. Die großen Deutschen, volume 2, Berlin: Ullstein Verlag.
- Simmons, J. (1996). The giant book of scientists: The 100 greatest minds of all time, Sydney: The Book Company.
- Singh, Simon. (2000). Fermats letzter Satz, Munich: Deutscher Taschenbuch Verlag.
- Lexikon der Naturwissenschaftler, Spektrum Akademischer Verlag Heidelberg, 2000.
Xem thêm[sửa]
Liên kết ngoài[sửa]
Liên kết đến đây
- Carl Friedrich Gauss
- Phương trình Pell
- Carl Friedrich Gauß
- Cơ học cổ điển
- Hình học
- Lý thuyết số
- Nga
- Pi
- Số học
- Số phức
- Xem thêm liên kết đến trang này.