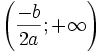Đại số 10/Chương II/§3. Hàm số bậc hai
Mục lục
Lí thuyết[sửa]
Tập
xác
định
của
hàm
số
này
là
D
=
ℝ.
Khi
b
=
c
=
0
ta
được
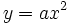 -
hàm
số
đã
được
học
ở
lớp
9.
-
hàm
số
đã
được
học
ở
lớp
9.
Đồ thị của hàm số bậc hai[sửa]
| Hoạt động 1 |
Nhắc
lại
các
kết
quả
đã
biết
về
đồ
thị
của
hàm
số
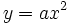 ?
? |
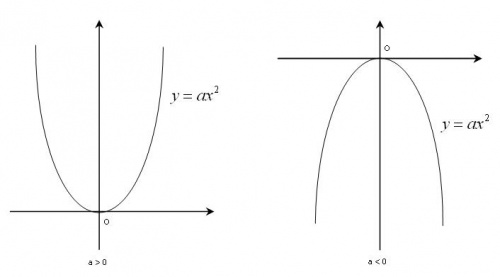
Nhận xét[sửa]
Đồ
thị
của
hàm
số
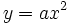 có
đỉnh
là
điểm
O(0;0),
là
điểm
thấp
nhất
của
đồ
thị
trong
trường
hợp
a
>
0
(y
≥
0
với
mọi
x),
và
là
điểm
cao
nhất
của
đồ
thị
trong
trường
hợp
a
<
0
(y
≤
0
với
mọi
x)
(hình
20).
có
đỉnh
là
điểm
O(0;0),
là
điểm
thấp
nhất
của
đồ
thị
trong
trường
hợp
a
>
0
(y
≥
0
với
mọi
x),
và
là
điểm
cao
nhất
của
đồ
thị
trong
trường
hợp
a
<
0
(y
≤
0
với
mọi
x)
(hình
20).
Đồ
thị
của
hàm
số
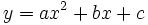 có
điểm
thấp
nhất
hoặc
điểm
cao
nhất
không?
có
điểm
thấp
nhất
hoặc
điểm
cao
nhất
không?
Thực hiện phép biến đổi đã biết ở lớp 9, ta có viết:
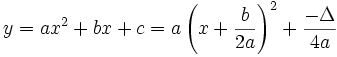 với
với
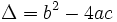 .
.Nhận xét rằng:
-
Nếu
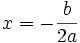 thì
thì
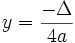 .
Vậy
điểm
.
Vậy
điểm
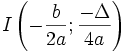 thuộc
đồ
thị
của
hàm
số
(1).
thuộc
đồ
thị
của
hàm
số
(1). -
Nếu
a
>
0
thì
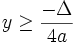 với
mọi
x,
do
đó
I
là
điểm
thấp
nhất
của
đồ
thị.
với
mọi
x,
do
đó
I
là
điểm
thấp
nhất
của
đồ
thị. -
Nếu
a
<
0
thì
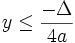 với
mọi
x,
do
đó
I
là
điểm
cao
nhất
của
đồ
thị.
với
mọi
x,
do
đó
I
là
điểm
cao
nhất
của
đồ
thị.
Như
vậy,
đồ
thị
của
hàm
số
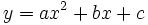 có
điểm
có
điểm
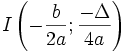 đóng
vai
trò
như
điểm
O(0;0)
của
đồ
thị
hàm
số
đóng
vai
trò
như
điểm
O(0;0)
của
đồ
thị
hàm
số
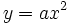 .
.
Đồ thị[sửa]
Dưới
đây(*)
ta
sẽ
thấy
đồ
thị
của
hàm
số
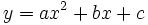 chính
là
đồ
thị
của
hàm
số
chính
là
đồ
thị
của
hàm
số
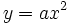 sau
một
số
phép
"dịch
chuyển"
trên
mặt
phẳng
tọa
độ.
sau
một
số
phép
"dịch
chuyển"
trên
mặt
phẳng
tọa
độ.
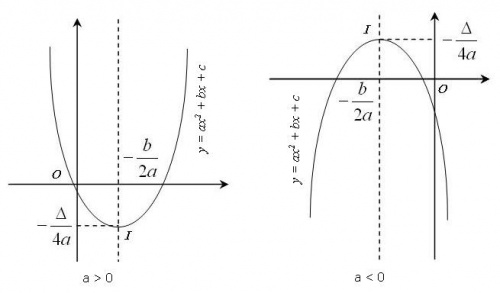
|
Đồ
thị
của
hàm
số
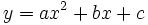 (a
≠
0)
là
một
đường
parabol
có
đỉnh
là
điểm
(a
≠
0)
là
một
đường
parabol
có
đỉnh
là
điểm
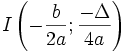 ,
có
trục
đối
xứng
là
đường
thẳng
,
có
trục
đối
xứng
là
đường
thẳng
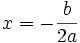 .
Parabol
này
quay
bề
lõm
lên
trên
nếu
a
>
0
và
xuống
dưới
nếu
a
<
0
(Hình
21).
.
Parabol
này
quay
bề
lõm
lên
trên
nếu
a
>
0
và
xuống
dưới
nếu
a
<
0
(Hình
21). |
|
Cách vẽ[sửa]
Để
vẽ
đường
parabol
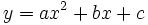 (a
≠
0),
ta
thực
hiện
các
bước:
(a
≠
0),
ta
thực
hiện
các
bước:
|
1.Xác
định
tọa
độ
của
đỉnh
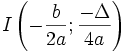 .
.
2.
Vẽ
trục
đối
xứng
3. Xác định tọa độ các giao điểm của parabol với trục tung (điểm (0;c)) và trục hoành (nếu có).
4. Vẽ parabol
|
|
| VÍ DỤ |
Vẽ
parabol
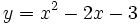 .
. |
| Lời giải | |
| Hoạt động 2 |
Vẽ
parabol
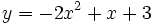 .
. |
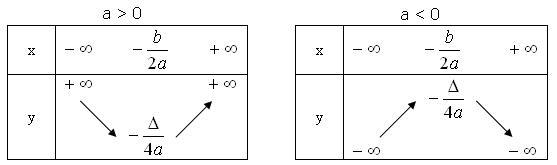
Chiều biến thiên của hàm số bậc hai[sửa]
Dựa
vào
đồ
thị
của
hàm
số
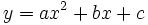 (a
≠
0),
ta
có
bảng
biến
thiên
của
nó
trong
hai
trường
hợp
a
>
0
và
a
<
0
như
sau:
(a
≠
0),
ta
có
bảng
biến
thiên
của
nó
trong
hai
trường
hợp
a
>
0
và
a
<
0
như
sau:
Từ
đó
ta
có
định
lí
dưới
đây
ĐỊNH LÍ
|
Nếu
a
>
0
thì
hàm
số
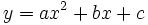
Nếu
a
<
0
thì
hàm
số
|
|
BÀI TẬP[sửa]
| 1. Xác định tọa độ của đỉnh và các giao điểm với trục tung, trục hoành (nếu có) của mỗi parabol: | |
a)
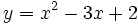
|
b)
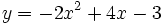
|
c)
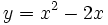
|
d)
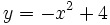
|
| 2. Lập bảng biến thiên và vẽ đồ thị của các hàm số: | |
a)
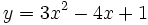
|
b)
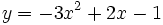
|
c)
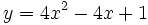
|
d)
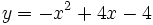
|
e)
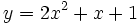
|
f)
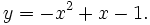
|
3.
Xác
định
parabol
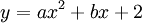 ,
biết
rằng
parabol
đó:
,
biết
rằng
parabol
đó: |
|
| a) Đi qua hai điểm M(1;5) và N(-2;8) |
b)
Đi
qua
điểm
A(3;-4)
và
có
trục
đối
xứng
là
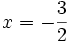
|
| c) Có đỉnh là I(2;-2) |
d)
Đi
qua
điểm
B(-1;6)
và
tung
độ
của
đỉnh
là
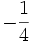 .
. |
4.
Xác
định
a,
b,
c
biết
parabol
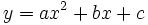 đi
qua
điểm
A(8;0)
và
có
đỉnh
là
I(6;-12).
đi
qua
điểm
A(8;0)
và
có
đỉnh
là
I(6;-12).