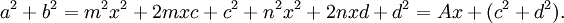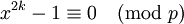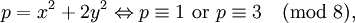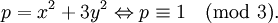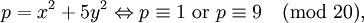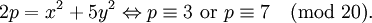Định lý Fermat về tổng hai số chính phuơng
Định lý Fermat về tổng của hai số chính phương phát biểu như sau:
- "Với mọi số nguyên tố lẻ p, biểu diễn được dưới dạng tổng của hai số chính phương:
-
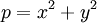 ,
với
x,y
là
các
số
tự
nhiên
lớn
hơn
0,
,
với
x,y
là
các
số
tự
nhiên
lớn
hơn
0, - khi và chỉ khi p đồng dư với 1 theo mô-đun 4."
Ví dụ:
- Các số nguyên tố lẻ 5, 13, 17, 29, 37, 41 đều đồng dư với 1 theo mô-đun 4, do đó chúng biểu diễn được dưới dạng tổng của hai số chính phương:
-
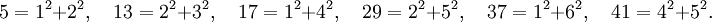
- Mặt khác, các số nguyên tố lẻ 3, 7, 11, 19, 23 và 31 đều đồng dư với 3 theo mô-đun 4, do đó chúng không thể biểu diễn được dưới dạng tổng của hai số chính phương.
Albert Girard là người đầu tiên đưa ra nhận xét rằng "mỗi số nguyên tố lẻ bất kì mà đồng dư với 1 theo mô-đun 4, đều biểu diễn được dưới dạng tổng của hai số chính phương" vào năm 1632 [1]. Fermat là người đưa ra chứng minh đầu tiên. Fermat đã thông báo điều này trong một lá thư gửi cho Marin Mersenne vào ngày 25 tháng 12 năm 1640, ngày giáng sinh; vì thế định lý này đôi khi còn được gọi là định lý ngày giáng sinh của Fermat.
Các chứng minh của định lý[sửa]
Nếu số nguyên tố lẻ p mà biểu diễn được dưới dạng tổng của hai số chính phương, do số chính phương khi chia cho 4 chỉ dư 0 hoặc 1, nên p chia cho 4 chỉ có thể dư 1. Điều kiện cần của định lý là hiển nhiên. Vấn đề còn lại là điều kiện đủ.
Chứng minh của Euler[sửa]
Euler đã chứng minh thành công "định lý Fermat về tổng của hai số chính phương" vào năm 1747, khi đã 40 tuổi. Ông thông báo điều này trong một lá thư gửi cho Goldbach vào ngày 6 tháng 5 năm 1747. Chứng minh gồm có 5 bước; bước thứ năm được trình bày trong một lá thư gửi cho Goldbach vào năm 1749.
Trong chứng minh trình bày dưới đây, bước 1,2,3 dựa hoàn toàn vào chứng minh của Euler, bước 4 và 5 có sửa đổi.
1. Tích của hai số, mà mỗi số là tổng của hai số chính phương, cũng là tổng của hai số chính phương:
-
Chứng
minh
điều
này
dựa
vào
định
thức
Brahmagupta–Fibonacci:
-
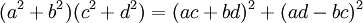 .
.
-
2.
Nếu
một
số
tự
nhiên
n
mà
chia
hết
cho
số
nguyên
tố
p,
và
cả
n
lẫn
p
đều
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương,
thì
 cũng
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương:
cũng
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương:
-
Trước
hết
ta
biểu
diễn:
-
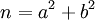
-
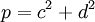 ,
với
a,b,c,d
là
các
số
tự
nhiên.
,
với
a,b,c,d
là
các
số
tự
nhiên.
-
-
Do:
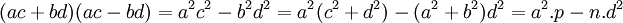 chia
hết
cho
p,
và
p
nguyên
tố,
nên
một
trong
hai
số
(ac+bd)
hoặc
(ac-bd)
chia
hết
cho
p.
chia
hết
cho
p,
và
p
nguyên
tố,
nên
một
trong
hai
số
(ac+bd)
hoặc
(ac-bd)
chia
hết
cho
p.
- Nếu(ac-bd) chia hết cho p.
- Sử dụng định thức Brahmagupta-Fibonacci, ta có:
-
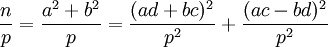 ,
, -
do
(ac-bd)
chia
hết
cho
p,
nên
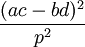 là
số
chính
phương,
mà
là
số
chính
phương,
mà
 nguyên,
nên
nguyên,
nên
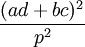 cũng
nguyên,
và
do
đó
là
số
chính
phương.
Suy
ra
cũng
nguyên,
và
do
đó
là
số
chính
phương.
Suy
ra
 cũng
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
cũng
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
-
Trường
hợp
còn
lại
(ac+bd)
chia
hết
cho
p,
lúc
này
ta
phân
tích:
-
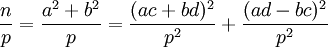 ,
và
lặp
lại
các
bước
tương
tự
như
trên.
,
và
lặp
lại
các
bước
tương
tự
như
trên.
-
3.
Nếu
n
chia
hết
cho
m,
mà
n
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương
còn
m
thì
không,
thì
tỷ
số
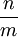 có
ước
không
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương:
có
ước
không
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương:
-
Chứng
minh
bằng
phản
chứng.
Giả
sử
mọi
ước
của
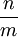 đều
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
Đặt:
đều
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
Đặt: -
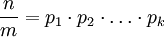 với
với
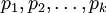 đều
là
các
số
nguyên
tố
(không
nhất
thiết
đôi
một
khác
nhau).
đều
là
các
số
nguyên
tố
(không
nhất
thiết
đôi
một
khác
nhau). -
Do
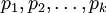 đều
biểu
diễn
thành
tổng
của
hai
số
chính
phương
được
cũng
nên
áp
dụng
bước
2
chia
n
liên
tiếp
k
lần
cho
đều
biểu
diễn
thành
tổng
của
hai
số
chính
phương
được
cũng
nên
áp
dụng
bước
2
chia
n
liên
tiếp
k
lần
cho
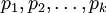 suy
ra:
suy
ra: -
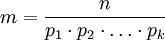 ,
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
,
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương. - Suy ra mâu thuẫn.
4.
Nếu
a
và
b
nguyên
tố
cùng
nhau
thì
mọi
ước
của
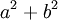 đều
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương:
đều
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương:
-
Chứng
minh
phản
chứng.
Giả
sử
tồn
tại
các
số
tự
nhiên
a,b
nguyên
tố
cùng
nhau
sao
cho
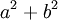 có
ít
nhất
một
ước
không
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
Trong
các
cặp
số
đó
ta
xét
cặp
(a,b)
thỏa
mãn
tổng
(a+b)
nhỏ
nhất.
có
ít
nhất
một
ước
không
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
Trong
các
cặp
số
đó
ta
xét
cặp
(a,b)
thỏa
mãn
tổng
(a+b)
nhỏ
nhất. -
Xét
x
là
ước
của
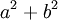 mà
không
thể
biểu
diễn
thành
tổng
của
2
số
chính
phương.
mà
không
thể
biểu
diễn
thành
tổng
của
2
số
chính
phương. -
Đặt:
-
 ,
trong
đó
c,d
là
số
tự
nhiên
lớn
hơn
0
và
không
vượt
quá
x-1.
,
trong
đó
c,d
là
số
tự
nhiên
lớn
hơn
0
và
không
vượt
quá
x-1.
-
-
Suy
ra:
-
-
Suy
ra
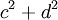 chia
hết
cho
x.
Nếu
c
và
d
nguyên
tố
cùng
nhau
thì
do
tổng
c+d
<
a+b
nên
mẫu
thuẫn
với
giả
thiết
về
tổng
(a+b)
là
nhỏ
nhất.
Vậy
ƯCLN
của
c
và
d
bằng
y
lớn
hơn
1.
chia
hết
cho
x.
Nếu
c
và
d
nguyên
tố
cùng
nhau
thì
do
tổng
c+d
<
a+b
nên
mẫu
thuẫn
với
giả
thiết
về
tổng
(a+b)
là
nhỏ
nhất.
Vậy
ƯCLN
của
c
và
d
bằng
y
lớn
hơn
1. - Nếu y và x không nguyên tố cùng nhau, thì tồn tại số nguyên tố p sao cho y và x cùng chia hết cho p, suy ra a,b cũng chia hết cho p (mâu thuẫn với giả thiết a và b nguyên tố cùng nhau).
- Vậy y và x nguyên tố cùng nhau.
-
Đặt:
-
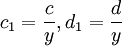 ,
,
-
-
thì
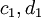 nguyên
tố
cùng
nhau
và
nguyên
tố
cùng
nhau
và
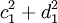 chia
hết
cho
x,
và
rõ
ràng
chia
hết
cho
x,
và
rõ
ràng
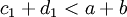 ,
mẫu
thuẫn
với
giả
thiết
về
tổng
(a+b)
là
nhỏ
nhất.
,
mẫu
thuẫn
với
giả
thiết
về
tổng
(a+b)
là
nhỏ
nhất. - Suy ra điều giả sử là sai. Ta có điều phải chứng minh.
5. Mọi số nguyên tố p lẻ có dạng 4k+1 đều biểu diễn thành tổng của hai số chính phương:
-
Theo
định
lý
Fermat
nhỏ,
các
số
sau
đây
đều
đồng
dư
với
1
theo
mô-đun
p:
-
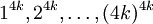 .
.
-
-
Xét
hiệu
giữa
hai
số
liên
tiếp
nhau:
-
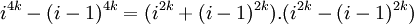 ,
với
i
chạy
từ
2
đến
4k.
,
với
i
chạy
từ
2
đến
4k.
-
-
Do
p
là
số
nguyên
tố,
nên
ít
nhất
một
trong
hai
số
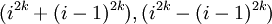 chia
hết
cho
p.
Nếu
tồn
tại
i
mà
chia
hết
cho
p.
Nếu
tồn
tại
i
mà
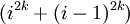 chia
hết
cho
p,
thì
theo
bước
4,
suy
ra
p
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương.
chia
hết
cho
p,
thì
theo
bước
4,
suy
ra
p
có
thể
biểu
diễn
thành
tổng
của
hai
số
chính
phương. -
Ngược
lại,
giả
sử
không
tồn
tại
i
mà
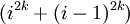 chia
hết
cho
p,
suy
ra:
chia
hết
cho
p,
suy
ra: -
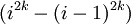 chia
hết
cho
p
với
mọi
i
chạy
từ
2
đến
4k.
Như
vậy
các
số
sau
đồng
dư
với
nhau
đôi
một
theo
mô-đun
p:
chia
hết
cho
p
với
mọi
i
chạy
từ
2
đến
4k.
Như
vậy
các
số
sau
đồng
dư
với
nhau
đôi
một
theo
mô-đun
p: -
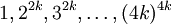 .
. -
Phương
trình
mô-đun:
-
- có 4k nghiệm, điều này mâu thuẫn với định lý Lagrange.
- Vậy điều giả sử là sai. Suy ra p có thể biểu diễn dưới dạng tổng của hai số chính phương.
Kết quả khác[sửa]
Fermat đã thông báo về 2 kết quả khác trong một lá thư gửi cho Blaise Pascal vào ngày 25 tháng 9 năm 1654:
Ông cũng viết:
- "Nếu hai số nguyên tố mà tận cùng là 3 hoặc 7, và lớn hơn 3 một bội của 4 mà nhân với nhau, thì tích của chúng bằng tổng của một số chính phương và 5 lần một số chính phương khác".
Nói một cách khác, nếu p, q có dạng 20k + 3 hoặc 20k + 7, thì pq = x2 + 5y2. Sau này, Euler đã mở rộng thành phỏng đoán sau:
Khẳng định của Fermat và phỏng đoán của Euler đều được Lagrange chứng minh.
Xem thêm[sửa]
Chú thích[sửa]
Lỗi
chú
thích:
Tồn
tại
thẻ
<ref>,
nhưng
không
tìm
thấy
thẻ
<references/>