Giáo án Hình học 11/Phép biến hình
Bài soạn dành cho tất cả các học sinh lớp 11, học theo sách giáo khoa Hình học 11 hoặc Hình học 11 Nâng cao[1]. Các hoạt động trong bài soạn được trình bày theo mẫu: phần nội dung được tách riêng biệt và đặt ở phía trên các hoạt động của giáo viên và học sinh.[2]
- Thời lượng thực hiện: 0,5 tiết
I) Mục tiêu[sửa]
Giúp học sinh
- 1) Kiến thức
- Hiểu được khái niệm về phép biến hình
- Biết được điều kiện để một quy tắc là một phép biến hình
- Làm quen với một số thuật ngữ và kí hiệu liên quan mà sau này thường dùng đến
- 2) Kỹ năng
- Dựng được ảnh của một điểm qua phép biến hình đã cho
- Làm việc độc lập với SGK theo chỉ dẫn của giáo viên
- 3) Tư duy
- Thao tác tư duy: So sánh, trừu tượng hóa và khái quát hóa
- Phẩm chất tư duy: Độc lập
- 4) Thái độ
- Cẩn thận trong vẽ hình và trình bày.
- Qua bài học HS biết được toán học có ứng dụng trong thực tiễn
II) Chuẩn bị[sửa]
- 1) Giáo viên
- Bảng phụ, thước thẳng, compa
- 2) Học sinh
- Kĩ năng: vẽ một điểm thỏa mãn đẳng thức vecto cho trước
- Dụng cụ: thước thẳng, vở nháp, compa
III) Tiến trình[sửa]
Hoạt động 1: Hình thành khái niệm PBH theo con đường quy nạp[sửa]
|
1) Định nghĩa (SGK) Quy tắc đặt tương ứng mỗi điểm M của mặt phẳng với một điểm xác định duy nhất M’ của mặt phẳng đó được gọi là phép biến hình trong mặt phẳng. Điểm M’ được gọi là ảnh của điểm M qua phép biến hình đó. |
| HĐGV | HĐHS |
|---|---|
|
-Dẫn nhập: Để hiểu pbh là gì, hãy giải các bài toán sau[3] vào vở nháp
-YC: HS1, HS2, HS3 lên bảng trình bày BT1, BT2 và BT3 -Tổ chức cho cả lớp nhận xét bài làm của 3 HS trên bảng -Thông báo: Ở cả 3 bài toán trên đều đề cập đến một vấn đề, đó là "Cho một quy tắc đặt tương ứng với mỗi điểm M cho trước với điểm M', biết điểm M' thỏa mãn điều kiện gì đó. Hãy xác định điểm M'?".[5] -Câu hỏi là: Trong các quy tắc trên, ứng với mỗi điểm M, quy tắc nào cho ta xác định duy nhất một điểm M’?[6] -Thông báo: Các quy tắc trong BT1 và BT2 được gọi là các phép biến hình. Vậy, phép biến hình là gì? Đọc và trình bày định nghĩa về pbh trong SGK vào vở. -Thông báo: Vẫn trong định nghĩa này, hãy ghi thêm câu "Điểm M’ được gọi là ảnh của điểm M qua phép biến hình đó."[7] vào cuối định nghĩa. |
-Đọc đề bài của 3 bài toán và giải vào vở nháp -3 HS lên bảng giải các BT được giao, số còn lại tiếp tục làm ra nháp -Chú ý lên bảng, phát biểu ý kiến nếu có và chính xác hóa bài làm của mình -Chú ý lên bảng, theo dõi trình bày của giáo viên[8] -Lần lượt kiểm nghiệm hình vẽ của 3 bài toán:
-Đọc SGK và ghi định nghĩa vào vở -Ghi thêm câu "Điểm M’ được gọi là ảnh của điểm M qua phép biến hình đó." vào định nghĩa. |
Hoạt động 2: Củng cố khái niệm qua ví dụ và phản ví dụ[sửa]
|
Ví
dụ
Trong mặt phẳng, cho đường tròn (O) và một điểm M nằm ngoài đường tròn (O). Quy tắc đặt tương ứng mỗi điểm M với điểm M’ như sau có là một phép biến hình không? Vì sao? a) M’ là giao điểm của đoạn thẳng OM với đường tròn b) M’ là giao điểm của đường thẳng OM với đường tròn
Giải
a) Quy tắc này là một phép biến hình, vì với mỗi điểm M ta chỉ xác định được duy nhất 1 điểm M’. b) Quy tắc này không là phép biến hình, vì với mỗi điểm M ta xác định được 2 điểm M’. |
| HĐGV | HĐHS |
|---|---|
|
Xét
quy
tắc:
“Trong
mặt
phẳng,
cho
đường
tròn
(O)
và
một
điểm
M
nằm
ngoài
đường
tròn
(O).
Quy
tắc
đặt
tương
ứng
mỗi
điểm
M
với
điểm
M’
như
sau
có
là
một
phép
biến
hình
không?
Vì
sao?
a) M’ là giao điểm của đoạn thẳng OM với đường tròn b) M’ là giao điểm của đường thẳng OM với đường tròn” |
a) là một phép biến hình , vì xác định được duy nhất một điểm M’ b) không phép biến hình, vì xác định được hai điểm M’ |
Hoạt động 3: Giới thiệu thuật ngữ và kí hiệu[sửa]
|
2)
Kí
hiệu
và
thuật
ngữ
Nếu kí hiệu một phép biến hình nào đó là F và M’ là ảnh của M qua phép biến hình F thì ta viết F(M) = M’ hoặc M’ = F(M). Khi đó, ta còn nói phép biến hình F biến điểm M thành điểm M’ Với mỗi hình H, nếu hình H’ gồm các điểm M’ là ảnh của điểm M nào đó trong hình H thì ta nói phép biến hình F biến hình H thành hình H’ hay hình H’ là ảnh của hình H qua phép biến hình và viết H’ = F(H) hoặc F(H) = H’. Chú ý: Phép biến hình biến mỗi điểm M thành chính nó được gọi là phép đồng nhất. |
| HĐGV | HĐHS |
|---|---|
| Thuyết trình[10] | Nghe, theo dõi và ghi vở |
Hoạt động 4: Gợi động cơ làm việc với phép tịnh tiến[sửa]
Tiếp theo ta sẽ làm quen với một phép biến hình “khá quen thuộc” – phép tịnh tiến. Phép tịnh tiến là gì?
Tài liệu tham khảo[sửa]
- SGK Hình học 11, NXB Giáo dục, 2007, trang 4
- SGK Hình học 11 Nâng cao, NXB Giáo dục, 2007, trang 4-5
- SGV Hình học 11, NXB Giáo dục, 2007, trang 7
- SGV Hình học 11 Nâng cao, NXB Giáo dục, 2007, trang 7
Chú thích[sửa]
- ↑ Nhà xuất bản Giáo dục, từ năm 2007
- ↑ Xem thêm về cách trình bày này tại: Thành viên:Nguyenthephuc/Note: Các mẫu giáo án#Mẫu hoạt động 2:
- ↑ Treo bảng phụ, với đề bài của 3 bài toán được ghi sẵn
- ↑ Bài này viết lại từ câu hỏi đầu tiên trong SGK Hình học 11 trang 4
- ↑ Vừa nói, giáo viên vừa quan sát lớp, vừa chỉ điểm M' tương ứng với điểm M ở mỗi hình vẽ và đảm bảo TẤT CẢ các học sinh đều theo dõi theo lên bảng.
- ↑ Nhấn mạnh từ "duy nhất" bằng cách sử dụng "ngắt câu", "giao tiếp mắt", cao giọng, kéo dài và dừng lại đủ lâu để đảm bảo cho học sinh suy nghĩ (tổng hợp) và trao đổi (thảo luận).
- ↑ SGK Hình học 11 (chương trình chuẩn) không có câu này, thiếu câu này sẽ khó dạy phần "thuật ngữ và kí hiệu"
- ↑ và thầm thắc mắc "Ổng ấy đang muốn nói điều gì nhỉ :D"
- ↑ Trường hợp học sinh không phát hiện ra là tồn tại "vô số" điểm M' thì giáo viên có thể dẫn dắt: "Em có thể tìm thêm 1 điểm M' khác với điểm M' đã có trên hình vẽ? Một điểm khác nữa, điểm khác nữa,... Vậy có thể tìm được bao nhiêu điểm M' thỏa mãn điều kiện đã cho?
- ↑ Nếu học sinh sử dụng SGK Nâng cao thì yêu cầu học sinh đọc SGK
Bản quyền[sửa]
Bản quyền của bài viết này thuộc về Nguyễn Thế Phúc <nguyenthephucmaster(at)gmail(dot)com>. Bạn ĐƯỢC phép sao chép để sử dụng cho mục đích học tập, nghiên cứu cá nhân, KHÔNG được sử dụng một phần hoặc toàn bộ bài viết cho mục đích thương mại và KHÔNG được phân phối lại bài viết này trên các trang mạng khác dưới mọi hình thức.
 và
điểm
M.
Tìm
điểm
M’
sao
cho
vecto
và
điểm
M.
Tìm
điểm
M’
sao
cho
vecto
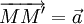 ?”
?”

