Giáo án Giải tích 12/Bài Kiểm cuối học kỳ I

Đề thi tham khảo

SỞ GIÁO DỤC VÀ ĐÀO TẠO                          ĐỀ KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
NAM ĐỊNH                                               NĂM HỌC: 2008-2009

                           Môn Toán lớp 12 THPT
           (Thời gian làm bài: 90 phút, không kể thời gian giao đề)

I. PHẦN CHUNG (7 điểm)

Câu 1 (3 điểm) Cho hàm số y = -x³ + 3x – 2

1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
2. Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x = -2.
3. Dựa vào đồ thị của hàm số đã cho, hãy biện luận theo tham số m số nghiệm của phương trình x³ – 3x + m = 0.

Câu 2 (2 điểm)

1. Cho hàm số y = xsinx + 2. Chứng minh rằng: y + y’’ – 2cos x không phụ thuộc vào x.
2. Tìm GTLN, GTNN của hàm số 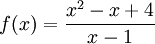$f(x)={\frac {x^{2}-x+4}{x-1}}$ trên đoạn [-2; 0].

Câu 3 (2,0 điểm) Cho hình lăng trụ ABC.A’B’C’ có hai đáy ABC và A’B’C’ là các tam giác vuông tại A và A’. Hình chiếu vuông góc của A trên mặt phẳng (A’B’C’) là trung điểm H của đoạn thẳng B’C’. Biết rằng AB = 1, 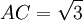$AC={\sqrt 3}$ ; AA’ = 2.

1. Tính thể tích của khối lăng trụ ABC.A’B’C’.
2. Tính diện tích của thiết diện tạo bởi mặt phẳng (AA’H) và lăng trục ABC.A’B’C’.

II. PHẦN RIÊNG (3 điểm)

Câu 4a (3,0 điểm, dành cho học sinh học chương trình Cơ bản)

1. Với hình lăng trụ ABC.A’B’C’ đã cho của Câu 3, hãy tính diện tích tam giác AC’A’ và tính khoảng cách từ điểm B’ đến mặt phẳng (AC’A’).
2. Giải phương trình: $\log _{5}x^{2}+{\frac {2}{\log _{5}x}}=5$

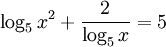
Câu 4b (3,0 điểm, dành cho học sinh học chương trình Nâng cao)

1. Với hình lăng trụ ABC.A’B’C’ đã cho của Câu 3, hãy xác định tâm và bán kính mặt cầu đi qua 4 điểm A, A’, B’ và C’.
2. Tìm tập xác định và xét chiều biến thiên của hàm số $f(x)=\ln \left({{\sqrt {x^{2}+1}}-x+1}\right)$

---

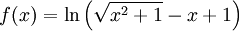
Các bài khác

I. PHÂN CHIA THEO HỌC KỲ VÀ TUẦN HỌC

Cả năm	78 tiết
Học kỳ I: 19 tuần (72 tiết)	48 tiết 6 tuần đầu x 2 tiết = 12 tiết 10 tuần tiếp x 3 tiết = 30 tiết 3 tuần cuối x 2 tiết = 6 tiết
Học kỳ II: 18 tuần (51 tiết)	30 tiết 6 tuần đầu x 1 tiết = 6 tiết 12 tuần cuối x 2 tiết = 24 tiết

Học kỳ I

Chương I – Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số

20 tiết

Tiết 1-3	Bài Sự đồng biến, nghịch biến của hàm số
Tiết 4-6	Bài Cực trị của hàm số
Tiết 7-9	Bài Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Tiết 10-11	Bài Đường tiệm cận
Tiết 12-18	Bài Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Tiết 19	Bài Ôn tập chương I
Tiết 20	Bài Kiểm tra chương I

Chương II - Hàm số luỹ thừa, hàm số mũ và hàm số lôgarit

17 tiết

Tiết 21-23	Bài Luỹ thừa
Tiết 24-25	Bài Hàm số luỹ thừa
Tiết 26-28	Bài Lôgarit
Tiết 29-31	Bài Hàm số mũ, hàm số lôgarit
Tiết 32-33	Bài Phương trình mũ và phương trình lôgarit
Tiết 34-35	Bài Bất phương trình mũ và lôgarit
Tiết 36	Bài Ôn tập chương II
Tiết 37	Bài Kiểm tra chương II

Chương III - Nguyên hàm, tích phân và ứng dụng

16 tiết

Tiết 38-43	Bài Nguyên hàm
Tiết 44-45	Bài Ôn tập học kỳ I
Tiết 46-47	Bài Kiểm cuối học kỳ I
Tiết 48	Trả bài kiểm tra cuối học kỳ I

Học kỳ II

Chương III - Nguyên hàm tích phân và ứng dụng (tiếp)

Tiết 49-52	Bài Tích phân
Tiết 53-56	Bài Ứng dụng của tích phân
Tiết 57	Bài Ôn tập chương III
Tiết 58	Bài Kiểm tra chương III

Chương IV - Số phức

19 tiết

Tiết 59-60	Bài Số phức
Tiết 61-62	Bài Cộng, trừ và nhân số phức
Tiết 63	Bài Phép chia số phức
Tiết 64-65	Bài Phương trình bậc hai với hệ số thực
Tiết 66	Bài Ôn tập chương IV
Tiết 67	Bài Kiểm tra chương IV
Tiết 68	Bài Ôn tập cuối năm
Tiết 69-70	Bài Kiểm tra cuối năm
Tiết 71	Trả bài kiểm tra cuối năm
Tiết 72-78	Tổng ôn tập tốt nghiệp

Xem thêm

• Giáo án Giải tích 12/Ôn thi tốt nghiệp
• Phân phối chương trình môn Toán lớp 12/2009-2010

Liên kết đến đây

• Giáo án Giải tích 12
• Giáo án Giải tích 12/Bài Sự đồng biến, nghịch biến của hàm số