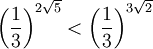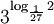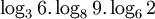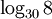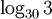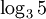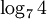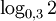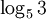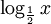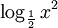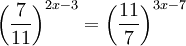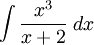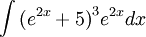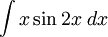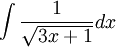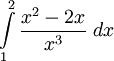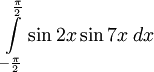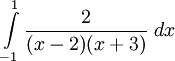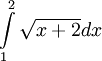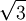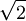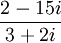Giải tích 12/Chuẩn kiến thức và kĩ năng/CTC
I. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số[sửa]
| Chủ đề | Mức độ cần đạt | Ghi chú |
|---|---|---|
| 1. Ứng dụng đạo hàm cấp một để xét tính đơn điệu của hàm số. |
Về
kiến
thức:
Biết mối liên hệ giữa sự đồng biến, nghịch biến của một hàm số và dấu đạo hàm cấp một của nó. Về kỹ năng: - Biết cách xét sự đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu đạo hàm cấp một của nó. |
Ví
dụ.
Xét
sự
đồng
biến,
nghịch
biến
của
các
hàm
số:
y
=
x4
-
2x2
+
3,
y
=
2x3
-
6x
+
2,
y
=
 .
. |
|
2.
Cực
trị
của
hàm
số.
Định nghĩa. Điều kiện đủ để có cực trị. |
Về
kiến
thức:
- Biết các khái niệm điểm cực đại, điểm cực tiểu, điểm cực trị của hàm số. - Biết các điều kiện đủ để có điểm cực trị của hàm số. Về kỹ năng: - Biết cách tìm điểm cực trị của hàm số. |
Ví dụ. Tìm các điểm cực trị của các hàm số y = x3(1 - x)2, y = 2x3 + 3x2 - 36x - 10. |
| 3. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số. |
Về
kiến
thức:
- Biết các khái niệm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập hợp số. Về kỹ năng: - Biết cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, một khoảng. |
Ví
dụ.
Tìm
giá
trị
lớn
nhất
và
giá
trị
nhỏ
nhất
của
hàm
số
y
=
x3
-
3x2
-
9x
+
35
trên
đoạn
[-
4;
4].
Ví dụ. Tính các cạnh của hình chữ nhật có chu vi nhỏ nhất trong tất cả các hình chữ nhật có diện tích 48m2. |
| 4. Đường tiệm cận của đồ thị hàm số. Định nghĩa và cách tìm các đường tiệm cận đứng, đường tiệm cận ngang. |
Về
kiến
thức:
- Biết khái niệm đường tiệm cận đứng, đường tiệm cận ngang của đồ thị. Về kỹ năng: - Biết cách tìm đường tiệm đứng, tiệm cận ngang của đồ thị hàm số. |
Ví
dụ.
Tìm
đường
tiệm
cận
đứng
và
đường
tiệm
cận
ngang
của
đồ
thị
các
hàm
số
y
=
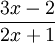 ;
y
=
;
y
=
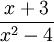 .
. |
| 5. Khảo sát hàm số. Sự tương giao của hai đồ thị. Cách viết phương trình tiếp tuyến của đồ thị hàm số. |
Về
kiến
thức:
- Biết các bước khảo sát và vẽ đồ thị hàm số (tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm tiệm cận, lập bảng biến thiên, vẽ đồ thị. Về kỹ năng: - Biết cách khảo sát và vẽ đồ thị của các hàm số y = ax4 + bx2 + c (a ≠ 0), y = ax3 + bx2 + cx + d (a ≠ 0)
và
y
= - Biết cách dùng đồ thị hàm số để biện luận số nghiệm của một phương trình. - Biết cách viết phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị hàm số. |
Ví
dụ.
Khảo
sát
và
vẽ
đồ
thị
các
hàm
số:
y
=
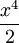 -
x2
-
-
x2
-
 ;
y
=
-
x3
+
3x
+1 ;
;
y
=
-
x3
+
3x
+1 ;
y
=
Ví dụ. Dựa vào đồ thị của hàm số y = x3 + 3x2, biện luận số nghiệm của phương trình x3 + 3x2 + m = 0 theo giá trị của tham số m. Ví dụ. Viết phương trình tiếp tuyến của đồ thị hàm số y = - x4 - 2x2 + 3 biết rằng hệ số góc của tiếp tuyến đó là - 8. Ví dụ. Viết phương trình tiếp tuyến của đồ thị hàm số y = 2x3 - 3x2 + 1 Tại điểm có hoành độ 2. |
II. Hàm số luỹ thừa, hàm số mũ và hàm số lôgarit[sửa]
| Chủ đề | Mức độ cần đạt | Ghi chú |
|---|---|---|
|
1.
Luỹ
thừa.
Định nghĩa luỹ thừa với số mũ nguyên, số mũ hữu tỉ, số mũ thực. Các tính chất. |
Về
kiến
thức:
- Biết các khái niệm luỹ thừa với số mũ nguyên của số thực, luỹ thừa với số mũ hữu tỉ và luỹ thừa với số mũ thực của số thực dương. - Biết các tính chất của luỹ thừa với số mũ nguyên, luỹ thừa với số mũ hữu tỉ và luỹ thừa với số mũ thực. Về kỹ năng: - Biết dùng các tính chất của luỹ thừa để đơn giản biểu thức, so sánh những biểu thức có chứa luỹ thừa. |
Ví
dụ.
Tính
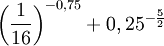
Ví dụ. Rút gọn biểu thức
Ví
dụ.
Chứng
minh
rằng
|
|
2.
Lôgarit.
Định nghĩa lôgarit cơ số a (a > 0, a ≠ 1) của một số dương. Các tính chất cơ bản của lôgarit. Lôgarit thập phân. Số e và lôgarit tự nhiên. |
Về
kiến
thức:
- Biết khái niệm lôgarit cơ số a (a > 0, a ≠ 1) của một số dương. - Biết các tính chất của lôgarit (so sánh hai lôgarit cùng cơ số, quy tắc tính lôgarit, đổi cơ số của lôgarit. - Biết các khái niệm lôgarit thập phân và lôgarit tự nhiên. Về kỹ năng: - Biết vận dụng định nghĩa để tính một số biểu thức chứa lôgarit đơn giản. - Biết vận dụng các tính chất của lôgarit vào các bài tập biến đổi, tính toán các biểu thức chứa lôgarit. |
Ví
dụ.
Tính
a
b
Ví
dụ.
Biểu
diễn
qua
và
Ví dụ. So sánh các số:
a
và
b
và
|
|
3.
Hàm
số
luỹ
thừa.
Hàm
số
mũ.
Hàm
số
lôgarit.
Định nghĩa, tính chất, đạo hàm và đồ thị. |
Về
kiến
thức:
- Biết khái niệm và tính chất của hàm số luỹ thừa, hàm số mũ, hàm số lôgarit. - Biết công thức tính đạo hàm của các hàm số luỹ thừa, hàm số mũ, hàm số lôgarit. - Biết dạng đồ thị của các hàm số luỹ thừa, hàm số mũ, hàm số lôgarit. Về kỹ năng: - Biết vận dụng tính chất của các hàm số mũ, hàm số lôgarit vào việc so sánh hai số, hai biểu thức chứa mũ và lôgarit. - Biết vẽ đồ thị các hàm số luỹ thừa, hàm số mũ, hàm số lôgarit. - Tính được đạo hàm các hàm số y = ex, y = lnx. |
Ví
dụ.
Vẽ
đồ
thị
của
các
hàm
số:
a
y
=
3.2x
b
y
=
Ví dụ. Vẽ đồ thị các hàm số:
a
y
=
2
b
y
=
Ví dụ. Tính đạo hàm của các hàm số: a y = 2xex + 3sin 2x ; b y = 5x2 - ln x + 8cos x. |
| 4. Phương trình, bất phương trình mũ và lôgarit. |
Về
kỹ
năng:
- Giải được phương trình, bất phương trình mũ: phương pháp đưa về luỹ thừa cùng cơ số, phương pháp lôgarit hoá, phương pháp dùng ẩn số phụ, phương pháp sử dụng tính chất của hàm số. - Giải được phương trình, bất phương trình lôgarit: phương pháp đưa về lôgarit cùng cơ số, phương pháp mũ hoá, phương pháp dùng ẩn số phụ. |
Ví
dụ.
Giải
phương
trình
Ví dụ. Giải phương trình 2.16x - 17.4x + 8 = . Ví dụ. Giải phương trình log4 (x + 2) = log2 x. Ví dụ. Giải bất phương trình 9x - 5. 3x + 6 < . Ví dụ. Giải bất phương trình log3 (x + 2 > log9 (x + 2). |
III. Nguyên hàm, tích phân và ứng dụng[sửa]
| Chủ đề | Mức độ cần đạt | Ghi chú |
|---|---|---|
|
1.
Nguyên
hàm.
Định nghĩa và các tính chất của nguyên hàm. Kí hiệu họ các nguyên hàm của một hàm số. Bảng nguyên hàm của một số hàm số sơ cấp. Phương pháp đổi biến số. Tính nguyên hàm từng phần. |
Về
kiến
thức:
- Hiểu khái niệm nguyên hàm của một hàm số. - Biết các tính chất cơ bản của nguyên hàm. Về kỹ năng: - Tìm được nguyên hàm của một số hàm số tương đối đơn giản dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần. - Sử dụng được phương pháp đổi biến số (khi đã chỉ rõ cách đổi biến số và không đổi biến số quá một lần) để tính nguyên hàm. |
Dùng
kí
hiệu
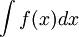 để
chỉ
họ
các
nguyên
hàm
của
f(x).
để
chỉ
họ
các
nguyên
hàm
của
f(x).
Ví
dụ.
Tính
Ví
dụ.
Tính
Ví
dụ.
Tính
Ví
dụ.
Tính
(Hướng dẫn: đặt u = 3x + 1). |
|
2.
Tích
phân.
Diện tích hình thang cong. Định nghĩa và các tính chất của tích phân. Phương pháp đổi biến số. Phương pháp tính tích phân từng phần. |
Về
kiến
thức:
- Biết khái niệm về diện tích hình thang cong. - Biết định nghĩa tích phân của hàm số liên tục bằng công thức Niu-tơn Lai-bơ-nit. - Biết các tính chất của tích phân. Về kỹ năng: - Tính được tích phân của một số hàm số tương đối đơn giản bằng định nghĩa hoặc phương pháp tính tích phân từng phần. - Sử dụng được phương pháp đổi biến số (khi đã chỉ rõ cách đổi biến số và không đổi biến số quá một lần) để tính tích phân. |
Khi
đổi
biến
số
cần
cho
trước
phép
đổi
biến
số.
Ví
dụ.
Tính
Ví
dụ.
Tính
Ví
dụ.
Tính
Ví
dụ.
Tính
(Hướng dẫn: đặt u = x + 2). |
| 3. Ứng dụng hình học của tích phân. |
Về
kiến
thức:
- Biết các công thức tính diện tích, thể tích nhờ tích phân. Về kỹ năng: - Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân. |
Ví
dụ.
Tính
diện
tích
hình
phẳng
giới
hạn
bởi
parabol
y
=
2
-
x2
và
đường
thẳng
y
=
-
x.
Ví dụ. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi trục hoành và parabol y = x(4 - x quay quanh trục hoành. |
IV. Số phức[sửa]
| Chủ đề | Mức độ cần đạt | Ghi chú |
|---|---|---|
| 1. Dạng đại số của số phức. Biểu diễn hình học của số phức. Các phép tính cộng, trừ, nhân, chia số phức. |
Về
kiến
thức:
- Biết dạng đại số của số phức. - Biết cách biểu diễn hình học của số phức, môđun của số phức, số phức liên hợp. Về kỹ năng: - Thực hiện được các phép tính cộng, trừ, nhân, chia số phức. |
Ví
dụ.
Tính:
a 5 + 2i - 3(-7 + 6i
b
(2
-
i(
+
i
c
(1
+ i2
d
|
| 2. Giải phương trình bậc hai với hệ số thực. |
Về
kỹ
năng:
Biết tìm nghiệm phức của phương trình bậc hai với hệ số thực (nếu Δ < 0). |
Ví
dụ.
Giải
phương
trình:
x2 + x + 1 = |
Nguồn[sửa]
- Tài liệu hướng dẫn dạy và học toán 12, Bộ Giáo dục và đào tạo, 2009
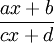 (ac
≠
0),
trong
đó
a,
b,
c,
d
là
các
số
cho
trước
.
(ac
≠
0),
trong
đó
a,
b,
c,
d
là
các
số
cho
trước
.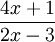 .
.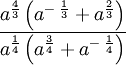 (a
>
0)
(a
>
0)