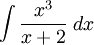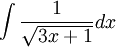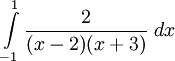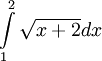Dạy học chủ đề Nguyên hàm và tích phân theo định hướng phát triển năng lực

Có thể vận dụng vào chủ đề Nguyên hàm và tích phân lớp 12 THPT.

Khi dạy học chủ đề Nguyên hàm và tích phân, HS ắt phải tính toán, tức là hướng vào hình thành năng lực tính toán trên các tập hợp số. Bên cạnh đó, HS còn phải biết sử dụng các công thức, kí hiệu, tức là hình thành được năng lực sử dụng ngôn ngữ toán học;

Nếu nhiệm vụ tính tích phân được xuất phát từ thực tiễn, liên môn thì còn rèn luyện được năng lực mô hình hoá toán học và năng lực GQVĐ;

Ngoài ra, máy tính cầm tay (MTCT) hỗ trợ tính tích phân. Do đó nếu được hướng dẫn HS còn có thể sử dụng MTCT tính tích phân, tức là hướng vào năng lực sử dụng công cụ tính toán.

Do đó, chủ đề này có thể hình thành và phát triển được năng lực tính toán cho HS.

Tích phân xác định được định nghĩa như diện tích S được giới hạn bởi đường cong y=f(x) và trục hoành, với x chạy từ a đến b (Ảnh: Wikipedia)

I. Chuẩn kiến thức, kĩ năng, thái độ theo chương trình hiện hành

Chủ đề	Mức độ cần đạt	Ghi chú
1. Nguyên hàm. Định nghĩa và các tính chất của nguyên hàm. Kí hiệu họ các nguyên hàm của một hàm số. Bảng nguyên hàm của một số hàm số sơ cấp. Phương pháp đổi biến số. Tính nguyên hàm từng phần.	Về kiến thức: - Hiểu khái niệm nguyên hàm của một hàm số. - Biết các tính chất cơ bản của nguyên hàm. Về kỹ năng: - Tìm được nguyên hàm của một số hàm số tương đối đơn giản dựa vào bảng nguyên hàm và cách tính nguyên hàm từng phần. - Sử dụng được phương pháp đổi biến số (khi đã chỉ rõ cách đổi biến số và không đổi biến số quá một lần) để tính nguyên hàm.	Dùng kí hiệu 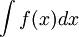$\int {f(x)dx}$ để chỉ họ các nguyên hàm của f(x). Ví dụ. Tính $\int {{\frac {{x^{3}}}{{x+2}}}}\;dx$ Ví dụ. Tính $\int {(e^{{2x}}+5{{)}}^{3}e^{{2x}}}dx$ Ví dụ. Tính $\int {x\sin 2x}\;dx$ Ví dụ. Tính $\int {{\frac {1}{{{\sqrt {3x+1}}}}}}dx$ (Hướng dẫn: đặt u = 3x + 1).
2. Tích phân. Diện tích hình thang cong. Định nghĩa và các tính chất của tích phân. Phương pháp đổi biến số. Phương pháp tính tích phân từng phần.	Về kiến thức: - Biết khái niệm về diện tích hình thang cong. - Biết định nghĩa tích phân của hàm số liên tục bằng công thức Niu-tơn  Lai-bơ-nit. - Biết các tính chất của tích phân. Về kỹ năng: - Tính được tích phân của một số hàm số tương đối đơn giản bằng định nghĩa hoặc phương pháp tính tích phân từng phần. - Sử dụng được phương pháp đổi biến số (khi đã chỉ rõ cách đổi biến số và không đổi biến số quá một lần) để tính tích phân.	Khi đổi biến số cần cho trước phép đổi biến số. Ví dụ. Tính $\int \limits _{1}^{2}{{\frac {{x^{2}-2x}}{{x^{3}}}}\;dx}$ Ví dụ. Tính $\int \limits _{{-{\frac {\pi }{2}}}}^{{{\frac {\pi }{2}}}}{\sin 2x\sin 7x\;dx}$ Ví dụ. Tính $\int \limits _{{-1}}^{1}{{\frac {2}{{(x-2{{)}}(x+3{{)}}}}}\;dx}$ Ví dụ. Tính $\int \limits _{1}^{2}{{\sqrt {x+2}}dx}$ (Hướng dẫn: đặt u = x + 2).
3. Ứng dụng hình học của tích phân.	Về kiến thức: - Biết các công thức tính diện tích, thể tích nhờ tích phân. Về kỹ năng: - Tính được diện tích một số hình phẳng, thể tích một số khối nhờ tích phân.	Ví dụ. Tính diện tích hình phẳng giới hạn bởi parabol y = 2 - x2 và đường thẳng y = - x. Ví dụ. Tính thể tích vật thể tròn xoay do hình phẳng giới hạn bởi trục hoành và parabol y = x(4 - x quay quanh trục hoành.

Xem chi tiết: Giải tích 12/Chuẩn kiến thức và kĩ năng/CTC#III. Nguyên hàm, tích phân và ứng dụng

II. Bảng mô tả các mức yêu cầu cần đạt cho mỗi loại câu hỏi/bài tập trong chủ đề

Nguyên hàm

NỘI DUNG		NHẬN BIẾT	THÔNG HIỂU	VẬN DỤNG THẤP	VẬN DỤNG CAO
Nguyên hàm	Định nghĩa nguyên hàm	-Phát biểu định nghĩa nguyên hàm. -Trong một sổ trưởng hợp đơn gián, nhận ra được hảm số F(x) có là nguyên hàm của một hàm sổ hay không.	Sử dụng định nghĩa để giải thích được một hàm sổ F(x) là hay không là một nguyên hàm của hám số f(x).	Sử dụng định nghĩa để tìm được nguyên hàm của hàm sổ đơn giản.	Sử dụng định nghĩa để tlm được một nguyên hảmcủa hàm sổ đơn giản, thoả mãn một điều kiện cho trước.
	Tính chất của nguyên hàm	- Nêu lên được tính chất của nguyên hàm. - Nhận ra được công thức diễn tả cho một tính chất của nguyên hàm.	Giải thích được các bước tính nguyên hàm dựa vào tính chất của nguyên hàm.	Tìm được nguyên hàm của một hàm sổ khí sừ dụng chỉ một tính chất cùa nguyên hàm.	Sử dụng phổi hợp các tích chất cùa nguyên hâm để tlm đượcnguyên hàm cùa một hàm số.

Tích phân

NỘI DUNG		NHẬN BIẾT	THÔNG HIỂU	VẬN DỤNG THẤP	VẬN DỤNG CAO
Tích phân	Phương pháp tích phâh	Phát biểu (viết ra) được công thức tính tỉch phân bằng phương pháp đổi biển số hay phương pháp tính tích phân từng phần, ở dạng tổng quát.	Giải thích được cách tính (các bước tỉnh) tích phân theo phương pháp đổi biến sổ hoặc pp tích phân từng phần.	Tính được giá trị tích phân, cùa một hàm sổ, trên một đoạn, khi đã chỉ rô phương pháp.	Tính được giá trị tích phân của một hàm số, trên một đoạn, khi chưa chỉ rõ phương pháp.
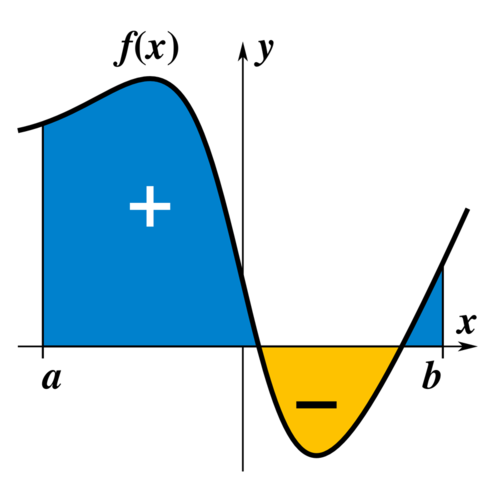
	Ứng dụng tích phân tính diện tích hình phẳng	Phát biểu (viết ra) được công thức tỉnh diện tích hình phẳng giới; hạn bời đồ thị hàm sổ y = f(x) (liên tục trên [a;b]) và các đường thẳng x = a, x = b, Ox.	Giải thích được cách tính diện tích hình phẳng (được giới hạn bởi các đường) có một trong các dạng sau: + y = f(x); y = g(x); x- a; x = b. + y = f(x); y = g(x); x = a; x = b. + y = f(x); y = g(x).	- Tính được diện tích hình phẳng (được giới hạn bởi các đường) có một trong các dạng sau: + y = f(x); y= g(x); x = a; x = b. + y = f(x); y=g(x); x = a; x = b. + y = f(x); y = g(x).	Tính được diện tích của một hình phẳng không có ngay một trong các dạng quen thuộc (mà phải chia hình đó thành một vài hình có dạng quen thuộc để tính).

Mời bạn đón đọc các bài viết tiếp theo bằng cách đăng kí nhận tin bài viết qua email hoặc like fanpage Thuvienkhoahoc.com để nhận được thông báo khi có cập nhật mới.

Nguồn

• Tài liệu tập huấn Dạy học và kiểm tra, đánh giá kết quả học tập theo định hướng phát triển năng lực học sinh; môn Toán cấp trung học phổ thông; Vụ giáo dục trung học; 2014

Bài liên quan

• Dạy học và kiểm tra đánh giá kết quả học tập theo định hướng phát triển năng lực học sinh cấp trung học phổ thông môn Sinh
• Kinh nghiệm quốc tế về phương pháp dạy học theo định hướng phát triển năng lực
• Kinh nghiệm của Việt Nam về phương pháp dạy học theo định hướng phát triển năng lực người học
• Kinh nghiệm quốc tế và trong nước về phương pháp dạy học theo định hướng phát triển năng lực người học
• Phương pháp và hình thức tổ chức dạy học theo định hướng phát triển năng lực

• « Mới nhất
• ‹ Mới hơn
• Cũ hơn ›

Liên kết đến đây

• Xác định các năng lực chung, cốt lõi và chuyên biệt của môn toán