Hình học 10/Chương I/§1. Các định nghĩa
Mục lục
Lí thuyết[sửa]
Khái niệm vectơ[sửa]
Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểm đầu, điểm B làm điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói đoạn thẳng AB là một đoạn thẳng có hướng.
|
Vectơ
là
một
đoạn
thẳng
có
hướng
|
|
Vectơ
có
điểm
đầu
A,
điểm
cuối
B
được
kí
hiệu
là
 và
đọc
là
"vectơ
AB".
Để
vẽ
vectơ
và
đọc
là
"vectơ
AB".
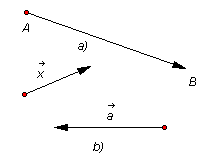
Để
vẽ
vectơ
 ta
vẽ
đoạn
thẳng
AB
và
đánh
dấu
mũi
tên
tên
ở
mút
B
(hình
1-2a).
ta
vẽ
đoạn
thẳng
AB
và
đánh
dấu
mũi
tên
tên
ở
mút
B
(hình
1-2a).
Vectơ
còn
được
kí
hiệu
là
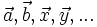 khi
không
cần
chỉ
rõ
điểm
đầu
và
điểm
cuối
của
nó
(hình
1-2b).
khi
không
cần
chỉ
rõ
điểm
đầu
và
điểm
cuối
của
nó
(hình
1-2b).
| Hoạt động 1 |
Với
hai
điểm
phân
biệt
A,
B
ta
có
bao
nhiêu
vectơ
có
điểm
đầu
và
điểm
cuối
là
A
hoặc
B.
|
Vectơ cùng phương, vectơ cùng hướng[sửa]
Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.
| Hoạt động 2 |
Nhận
xét
gì
về
vị
trí
tương
đối
giữa
các
giá
của
các
cặp
vectơ
sau:
 và
và
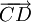 ,
,
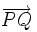 và
và
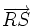 ,
,
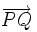 và
và
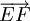 ,
,
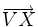 và
và
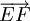 ,
,
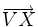 và
và
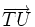
|
|
Hai
vectơ
được
gọi
là
cùng
phương
nếu
giá
của
chúng
song
song
hoặc
trùng
nhau.
|
|
Trên
hình
1-3,
hai
vectơ
 và
và
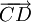 cùng
phương
và
có
cùng
hướng
đi
từ
trái
sang
phải.
Ta
nói
cùng
phương
và
có
cùng
hướng
đi
từ
trái
sang
phải.
Ta
nói
 và
và
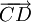 là
hai
vectơ
cùng
hướng.
Hai
vectơ
là
hai
vectơ
cùng
hướng.
Hai
vectơ
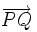 và
và
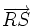 cùng
phương
nhưng
có
hướng
ngược
nhau.
Ta
nói
hai
vectơ
cùng
phương
nhưng
có
hướng
ngược
nhau.
Ta
nói
hai
vectơ
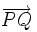 và
và
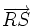 là
hai
vectơ
ngược
hướng.
là
hai
vectơ
ngược
hướng.
Như vậy, nếu hai vectơ cùng phương thì chúng chỉ có thể cùng hướng hoặc ngược hướng.
NHẬN
XÉT:
Ba
điểm
phân
biệt
A,
B,
C
thẳng
hàng
khi
và
chỉ
khi
hai
vectơ
 và
và
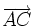 cùng
phương.
cùng
phương.
CHỨNG MINH
-
Thuận:
nếu
ba
điểm
A,
B,
C
thẳng
hàng
thì
hai
vectơ
 và
và
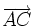 có
giá
trùng
nhau
nên
chúng
cùng
phương.
có
giá
trùng
nhau
nên
chúng
cùng
phương.
-
Đảo:
nếu
hai
vectơ
 và
và
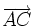 cùng
phương
thì
hai
đường
thẳng
AB
và
AC
song
song
với
nhau
hoặc
trùng
nhau.
Vì
chúng
có
chung
điểm
A
nên
chúng
phải
trùng
nhau.
Vậy
ba
điểm
A,
B,
C
thẳng
hàng.
cùng
phương
thì
hai
đường
thẳng
AB
và
AC
song
song
với
nhau
hoặc
trùng
nhau.
Vì
chúng
có
chung
điểm
A
nên
chúng
phải
trùng
nhau.
Vậy
ba
điểm
A,
B,
C
thẳng
hàng.
| Hoạt động 3 |
Khẳng
định
sau
đúng
hay
sai:
Nếu
ba
điểm
phân
biệt
A,
B,
C
thẳng
hàng
thì
hai
vectơ
|
Hai vectơ bằng nhau[sửa]
Mỗi
vectơ
có
một
độ
dài,
đó
là
khoảng
cách
giữa
điểm
đầu
và
điểm
cuối
của
vectơ
đó.
Độ
dài
của
vectơ
 được
kí
hiệu
là
được
kí
hiệu
là
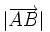 ,
như
vậy
,
như
vậy
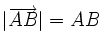 .
.
Vectơ có độ dài bằng 1 gọi là vectơ đơn vị.
CHÚ
Ý:
Khi
cho
trước
vectơ
 và
điểm
O,
thì
ta
luôn
tìm
được
một
điểm
A
duy
nhất
sao
cho
và
điểm
O,
thì
ta
luôn
tìm
được
một
điểm
A
duy
nhất
sao
cho
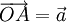 .
.
| Hoạt động 4 |
Gọi
O
là
tâm
hình
lục
giác
đều
ABCDEF.
Hãy
chỉ
ra
các
vectơ
bằng
vectơ
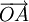 .
. |
Vectơ-không[sửa]
Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.
Bây
giờ
với
mọi
điểm
A
bất
kì
ta
quy
ước
có
một
vectơ
đặc
biệt
mà
điểm
đầu
và
điểm
cuối
đều
là
A.
Vectơ
này
được
kí
hiệu
là
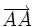 và
gọi
là
vectơ-không.
và
gọi
là
vectơ-không.
Vectơ
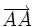 nằm
trên
đường
thẳng
đi
qua
A,
vì
vậy
ta
quy
ước
vectơ-không
cùng
phương,
cùng
hướng
với
mọi
vectơ.
Ta
cũng
quy
ước
rằng
nằm
trên
đường
thẳng
đi
qua
A,
vì
vậy
ta
quy
ước
vectơ-không
cùng
phương,
cùng
hướng
với
mọi
vectơ.
Ta
cũng
quy
ước
rằng
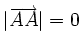 .
Do
đó
có
thể
coi
mọi
vectơ-không
đều
bằng
nhau.
Ta
kí
hiệu
vectơ-không
là
.
Do
đó
có
thể
coi
mọi
vectơ-không
đều
bằng
nhau.
Ta
kí
hiệu
vectơ-không
là
 .
.
NHẬN
XÉT:
-
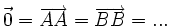 với
mọi
điểm
A,
B,...
với
mọi
điểm
A,
B,...
BÀI TẬP[sửa]
1.
Cho
ba
vectơ
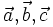 đều
khác
đều
khác
 .
Các
khẳng
định
sau
đúng
hay
sai?
.
Các
khẳng
định
sau
đúng
hay
sai?
-
a)
Nếu
hai
vectơ
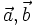 cùng
phương
với
cùng
phương
với
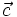 thì
thì
 và
và
 cùng
phương.
cùng
phương. -
b)
Nếu
hai
vectơ
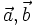 cùng
ngược
hướng
với
cùng
ngược
hướng
với
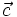 thì
thì
 và
và
 cùng
hướng.
cùng
hướng.
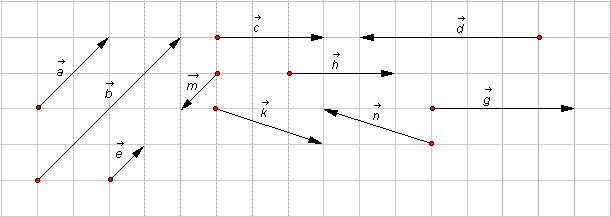
2. Trong hình, hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau:
3.
Cho
tứ
giác
ABCD.
Chứng
minh
rằng
tứ
giác
đó
là
hình
bình
hành
khi
và
chỉ
khi
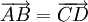 .
.
4. Cho lục giác đều ABCDEF có tâm O.
-
a)
Tìm
các
vectơ
khác
 và
cùng
phương
với
và
cùng
phương
với
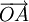 .
. -
b)
Tìm
các
vectơ
bằng
vectơ
 .
.
Xem thêm[sửa]
- Euclidean vector - Wikipedia




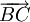 cùng
phương.
cùng
phương.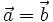 ,
nếu
chúng
cùng
hướng
và
có
cùng
độ
dài.
,
nếu
chúng
cùng
hướng
và
có
cùng
độ
dài.