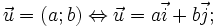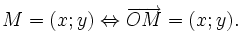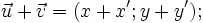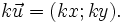Hình học 10/Chương I/Ôn tập chương I
Mục lục
Tóm tắt những kiến thức cần nhớ[sửa]
Vectơ
-
Vectơ
khác
 là
một
đoạn
thẳng
có
hướng.
Vectơ-không
có
điểm
đầu
và
điểm
cuối
trùng
nhau.
Vectơ-không
có
độ
dài
bằng
0,
có
phương
và
hướng
tùy
ý.
là
một
đoạn
thẳng
có
hướng.
Vectơ-không
có
điểm
đầu
và
điểm
cuối
trùng
nhau.
Vectơ-không
có
độ
dài
bằng
0,
có
phương
và
hướng
tùy
ý. - Hai vectơ bằng nhau nếu chúng có cùng hướng và cùng độ dài.
Tổng và hiệu của các vectơ
- Quy tắc ba điểm: Với ba điểm M, N, P bất kì, ta có:
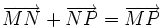
- Quy tắc hình bình hành: Nếu OABC là hình bình hành thì
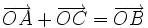
-
Quy
tắc
về
hiệu
vectơ:
Cho
vectơ
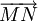 .
Với
điểm
O
bất
kì,
ta
có:
.
Với
điểm
O
bất
kì,
ta
có:
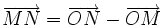
Tích của một vectơ với một số
-
Nếu
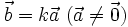 thì
thì
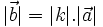 và
và
-
 cùng
hướng
với
cùng
hướng
với
 khi
k
≥
0.
khi
k
≥
0. -
 ngược
hướng
với
ngược
hướng
với
 khi
k
<
0.
khi
k
<
0.
-
- Các tính chất:
-
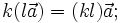
-
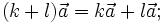
-
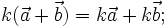
-
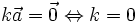 hoặc
hoặc
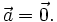
- Điểm I là trung điểm đoạn thẳng AB khi và chỉ khi với điểm O bất kì, ta có
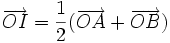
- Điểm G là trọng tâm tam giác ABC khi và chỉ khi với điểm O bất kì, ta có:
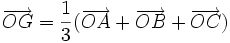
Tọa độ của vectơ và của điểm
-
Đối
với
hệ
trục
tọa
độ
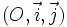 hay
Oxy:
hay
Oxy:
-
Nếu
A
=
(x;
y),
B
=
(x';
y')
thì
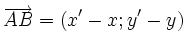 .
. -
Nếu
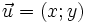 và
và
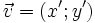 thì
thì
Câu hỏi tự kiểm tra[sửa]
1. Hãy nói rõ vectơ khác đoạn thẳng như thế nào?
2.
Nếu
hai
vectơ
 và
và
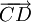 bằng
nhau
và
có
giá
không
trùng
nhau
thì
bốn
đỉnh
A,
B,
C,
D
có
là
bốn
đỉnh
của
một
hình
bình
hành
không?
bằng
nhau
và
có
giá
không
trùng
nhau
thì
bốn
đỉnh
A,
B,
C,
D
có
là
bốn
đỉnh
của
một
hình
bình
hành
không?
3. Nếu có nhiều vectơ thì xác định tổng của chúng như thế nào?
4. Hiệu hai vectơ được định nghĩa qua khái niệm tổng hai vectơ như thế nào?
5. Cho hai điểm A, B phân biệt. Với một điểm O bất kì, mỗi đẳng thức sau đây đúng hay sai?
a)
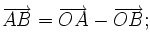
|
b)
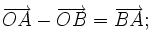
|
c)
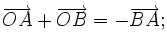
|
d)
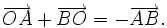
|
6. Có thể dùng phép nhân vectơ với một số để định nghĩa vectơ đối của một vectơ hay không?
7.
Cho
hai
vectơ
 và
và
 không
cùng
phương.
Trong
các
vectơ
không
cùng
phương.
Trong
các
vectơ
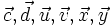 sau
đây,
hãy
chỉ
ra
các
vectơ
cùng
hướng
và
các
vectơ
ngược
hướng
sau
đây,
hãy
chỉ
ra
các
vectơ
cùng
hướng
và
các
vectơ
ngược
hướng
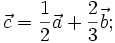 |
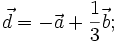 |
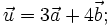 |
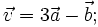 |
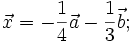 |
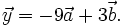 |
Hai
vectơ
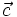 và
và
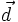 có
cùng
phương
hay
không?
Tại
sao?
có
cùng
phương
hay
không?
Tại
sao?
8. Cho tam giác ABC với trung tuyến AM và trọng tâm G. Mỗi khẳng định sau đây đúng hay sai?
a)
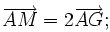
|
b)
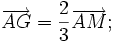
|
c)
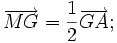
|
d)
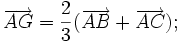
|
e)
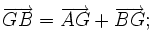
|
9. Cho biết tọa độ hai điểm A và B. Làm thế nào để:
-
a)
Tìm
tọa
độ
của
vectơ
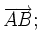
- b) Tìm tọa độ trung điểm của một đoạn thẳng AB?
10. Cho biết tọa độ ba đỉnh của một tam giác. Làm thế nào để tìm tọa độ trọng tâm tam giác đó?
Bài tập[sửa]
1.
Cho
lục
giác
đều
ABCDEF
có
tâm
O.
Hãy
chỉ
ra
các
vectơ
bằng
 có
điểm
đầu
và
điểm
cuối
là
O
hoặc
các
đỉnh
của
lục
giác.
có
điểm
đầu
và
điểm
cuối
là
O
hoặc
các
đỉnh
của
lục
giác.
2.
Cho
hai
vectơ
 và
và
 đều
khác
đều
khác
 .
Các
khẳng
định
sau
đúng
hay
sai?
.
Các
khẳng
định
sau
đúng
hay
sai?
a)
Hai
vectơ
 và
và
 cùng
hướng
thì
cùng
phương.
cùng
hướng
thì
cùng
phương.
b)
Hai
vectơ
 và
và
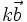 cùng
phương.
cùng
phương.
c)
Hai
vectơ
 và
và
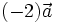 cùng
hướng.
cùng
hướng.
d)
Hai
vectơ
 và
và
 ngược
hướng
với
vectơ
thứ
ba
khác
ngược
hướng
với
vectơ
thứ
ba
khác
 thì
cùng
phương.
thì
cùng
phương.
3.
Tứ
giác
ABCD
là
hình
gì
nếu
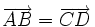 và
và
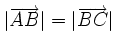 .
.
4.
Chứng
minh
rằng
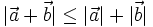 .
.
| 5. Cho tam giác ABC nội tiếp trong đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho. | ||
a)
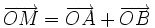
|
b)
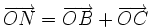
|
c)
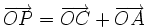 .
. |
6. Cho tam giác đều ABC có cạnh bằng a. Tính
a)
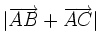 b)
b)
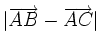 .
.
7. Cho sáu điểm M, N, P, Q, R, S bất kì. Chứng minh rằng
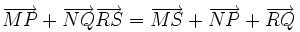
| 8. Cho tam giác OAB. Gọi M và N lần lượt là trung điểm của OA và OB. Tìm các số m, n sao cho. | |
a)
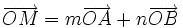
|
b)
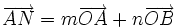
|
c)
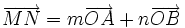
|
d)
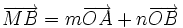
|
9.
Chứng
minh
rằng
nếu
G
và
G'
lần
lượt
là
trọng
tâm
của
các
tam
giác
ABC
và
A'B'C'
thì
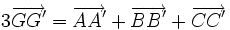 .
.
10. Trong mặt phẳng tọa độ Oxy, các khẳng định sau đúng hay sai?
a) Hai vectơ đối nhau thì chúng có hoành độ đối nhau.
b)
Vectơ
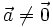 cùng
phương
với
vectơ
cùng
phương
với
vectơ
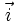 nếu
nếu
 có
hoành
độ
bằng
0.
có
hoành
độ
bằng
0.
c)
Vectơ
 có
hoành
độ
bằng
0
thì
cùng
phương
với
vectơ
có
hoành
độ
bằng
0
thì
cùng
phương
với
vectơ
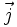 .
.
11.
Cho
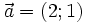 ,
,
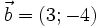 ,
,
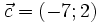 .
.
a)
Tìm
tọa
độ
của
vectơ
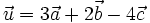 .
.
b)
Tìm
tọa
độ
vectơ
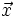 sao
cho
sao
cho
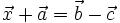 .
.
c)
Tìm
các
số
k
và
h
sao
cho
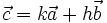 .
.
12.
Cho
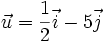 ,
,
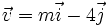 .
Tìm
m
để
.
Tìm
m
để
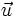 và
và
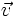 cùng
phương.
cùng
phương.
13. Trong các khẳng định sau, khẳng định nào là đúng?
a) Điểm A nằm trên trục hoành thì có hoành độ bằng 0.
b) P là trung điểm của đoạn thẳng AB khi và chỉ khi hoành độ của P bằng trung bình cộng các hoành độ của A và B.
c) Nếu tứ giác ABCD là hình bình hành thì trung bình cộng các tọa độ tương ứng của A và C bằng trung bình cộng các tọa độ tương ứng của B và D.
Bài tập trắc nghiệm[sửa]
1.
Cho
tứ
giác
ABCD.
Số
các
vectơ
khác
 có
điểm
đầu
và
điểm
cuối
là
đỉnh
của
tứ
giác
bằng:
có
điểm
đầu
và
điểm
cuối
là
đỉnh
của
tứ
giác
bằng: |
|||
| (A) 4 | (B) 6 | (C) 8 | (D) 12. |
2.
Cho
lục
giác
đều
ABCDEF
có
tâm
O.
Số
các
vectơ
khác
 cùng
phương
với
cùng
phương
với
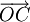 có
điểm
đầu
và
điểm
cuối
là
đỉnh
của
lục
giác
bằng
có
điểm
đầu
và
điểm
cuối
là
đỉnh
của
lục
giác
bằng |
|||
| (A) 4 | (B) 6 | (C) 7 | (D) 8. |
3.
Cho
lục
giác
đều
ABCDEF
có
tâm
O.
Số
các
vectơ
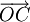 có
điểm
đầu
và
điểm
cuối
là
đỉnh
của
lục
giác
bằng
có
điểm
đầu
và
điểm
cuối
là
đỉnh
của
lục
giác
bằng |
|||
| (A) 2 | (B) 3 | (C) 4 | (D) 6 |
4.
Cho
hình
chữ
nhật
ABCD
có
AB
=
3,
BC
=
4.
Độ
dài
của
vectơ
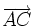 là:
là: |
|||
| (A) 5 | (B) 6 | (C) 7 | (D) 9 |
| 5. Cho ba điểm phân biệt A, B, C. Đẳng thức nào sau đây là đúng? | |
(A)
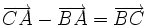
|
(B)
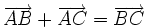
|
(C)
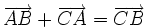
|
(D)
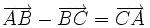
|
| 6. Cho hai điểm phân biệt A, B. Điều kiện để điêm I là trung điểm của đoạn thẳng AB là | |
| (A) IA = IB |
(B)
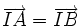
|
(C)
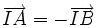
|
(D)
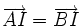
|
| 7. Cho tam giác ABC có G là trọng tâm, I là trung điểm của đoạn thẳng BC. Đẳng thức nào sau đây là đúng? | |
(A)
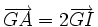
|
(B)
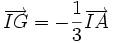
|
(C)
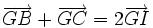
|
(D)
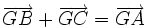
|
| 8. Cho hình bình hành ABCD. Đẳng thức nào sau đây là đúng? | |
(A)
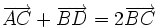
|
(B)
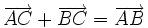
|
(C)
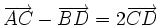
|
(D)
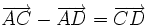 .
. |
| 9. Trong mặt phẳng tọa độ Oxy cho hình bình hành OABC, C nằm trên Ox. Khẳng định nào sau đây là đúng? | |
(A)
 có
tung
độ
khác
0
có
tung
độ
khác
0 |
(B) A và B có tung độ khác nhau. |
| (C) C có hoành độ bằng 0 | (D) xA + xC - xB = 0. |
10.
Cho
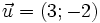 ,
,
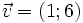 .
Khẳng
định
nào
sau
đây
là
đúng?
.
Khẳng
định
nào
sau
đây
là
đúng?
(A)
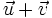 và
và
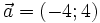 ngược
hướng.
ngược
hướng.
(B)
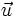 và
và
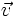 cùng
phương.
cùng
phương.
(C)
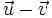 và
và
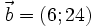 cùng
hướng.
cùng
hướng.
(D)
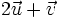 và
và
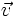 cùng
phương.
cùng
phương.
| 11. Cho tam giác ABC có A(3;5), B(1;2), C(5;2). Trọng tâm của tam giác ABC là: | |
| (A) G1(-3;4) | (B) G2(4;0) |
(C)
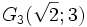
|
(D) G4(3;3). |
12.
Cho
bốn
điểm
A(1;1),
B(2;-1),
C(4;3),
D(3;5).
Chọn
mệnh
đề
đúng:
(A) Tứ giác ABCD là hình bình hành.
(B)
Điểm
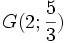 là
trọng
tâm
của
tam
giác
BCD.
là
trọng
tâm
của
tam
giác
BCD.
(C)
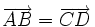
(D)
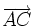 ,
,
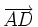 cùng
phương.
cùng
phương.
| 13. Trong mặt phẳng Oxy cho bốn điểm A(-5;-2), B(-5;3), C(3;3), D(3;-2). Khẳng định nào sau đây là đúng? | |
(A)
 và
và
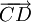 cùng
hướng.
cùng
hướng. |
(B) Tứ giác ABCD là hình chữ nhật |
| (C) Điểm I(-1;1) là trung điểm AC. |
(D)
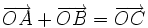
|
14.
Cho
tam
giác
ABC.
Đặt
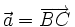 ,
,
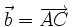 .
Các
cặp
vectơ
nào
sau
đây
cùng
phương?
.
Các
cặp
vectơ
nào
sau
đây
cùng
phương? |
|
(A)
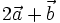 và
và
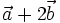
|
(B)
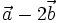 và
và
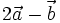
|
(C)
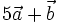 và
và
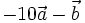
|
(D)
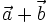 và
và
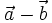 .
. |
| 15. Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có gốc O là tâm của hình vuông và các cạnh của nó song song với các trục tọa độ. Khẳng định nào sau đây là đúng? | |
(A)
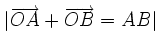
|
(B)
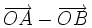 và
và
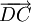 cùng
hướng.
cùng
hướng. |
| (C) xA = -xC và yA = yC | (D) xB = -xC và yC = -yB |
| 16. Kẻ MM1 vuông góc với Ox, MM2 vuông góc với Oy. Khẳng định nào sau đây là đúng? | |
(A)
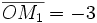
|
(B)
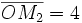
|
(C)
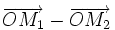 có
tọa
độ
(-3;-4)
có
tọa
độ
(-3;-4) |
(D)
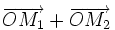 có
tọa
độ
(3;-4)
có
tọa
độ
(3;-4) |
| 17. Trong mặt phẳng tọa độ Oxy cho A(2;-3), B(4;7). Tọa độ trung điểm I của đoạn thẳng AB là | |
| (A) (6;4) | (B) (2;10) |
| (C) (3;2) | (D) (8;-21) |
18.
Trong
mặt
phẳng
tọa
độ
Oxy
cho
A(5;2),
B(10;8).
Tọa
độ
của
vectơ
 là
là |
|
| (A) (15;10) | (B) (2;4) |
| (C) (5;6) | (D) (50;16) |
19.
Cho
tam
giác
ABC
có
B(9;7),
C(11;-1),
M
và
N
lần
lượt
là
trung
điểm
của
AB
và
AC.
Tọa
độ
của
vectơ
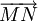 là
là |
|
| (A) (2;-8) | (B) (1;-4) |
| (C) (10;6) | (D) (5;3). |
20.
Trong
mặt
phẳng
tọa
độ
Oxy
cho
bốn
điểm
A(3;-2),
B(7;1),
C(0;1),
D(-8;-5).
Khẳng
định
nào
sau
đây
là
đúng?
(A)
 và
và
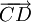 đối
nhau.
đối
nhau.
(B)
 và
và
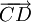 cùng
phương
nhưng
ngược
hướng.
cùng
phương
nhưng
ngược
hướng.
(C)
 và
và
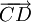 cùng
phương
và
cùng
hướng.
cùng
phương
và
cùng
hướng.
(D) A, B, C, D thẳng hàng.
| 21. Cho ba điểm A(-1;-5), B(5;5), C(-1;11). Khẳng định nào sau đây là đúng? | |
| (A) A, B, C thẳng hàng. |
(B)
 và
và
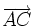 cùng
phương
cùng
phương |
(C)
 và
và
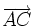 không
cùng
phương
không
cùng
phương |
(D)
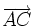 và
và
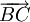 cùng
phương.
cùng
phương. |
22.
Cho
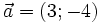 ,
,
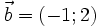 .
Tọa
độ
của
vectơ
.
Tọa
độ
của
vectơ
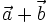 là
là |
|||
| (A) (-4;6) | (B) (2;-2) | (C) (4;-6) | (D) (-3;-8) |
23.
Cho
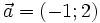 ,
,
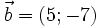 .
Tọa
độ
của
vectơ
.
Tọa
độ
của
vectơ
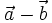 là
là |
|||
| (A) (6;-9) | (B) (4;-5) | (C) (-6;9) | (D) (-5;-14) |
24.
Cho
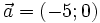 ,
,
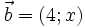 .
Hai
vectơ
.
Hai
vectơ
 và
và
 cùng
phương
nếu
số
x
là
cùng
phương
nếu
số
x
là |
|||
| (A) -5 | (B) 4 | (C) 0 | (D) -1 |
25.
Cho
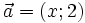 ,
,
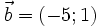 ,
,
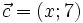 .
Vectơ
.
Vectơ
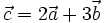 nếu
nếu |
|||
| (A) x = -15 | (B) x' = 3 | (C) x = 15 | (D) x = 5. |
| 26. Cho A(1;1), B(-2;-2), C(7;7). Khẳng định nào đúng? | |
| (A) G(2;2) là trọng tâm của tam giác ABC | (B) Điểm B ở giữa hai điểm A và C. |
| (C) Điểm A ở giữa hai điểm B và C. |
(D)
Hai
vectơ
 và
và
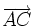 cùng
hướng.
cùng
hướng. |
| 27. Các điểm M(2;3), N(0;-4), P(-1;6) lần lượt là trung điểm các cạnh BC, CA, AB của tam giác ABC. Toạ độ đỉnh A của tam giác là: | |||
| (A) (1;5) | (B) (-3;-1) | (C) (-2;-7) | (D) (1;-10). |
| 28. Cho tam giác ABC có trọng tâm là gốc tọa độ O, hai đỉnh A và B có tọa độ A(-2;2), B(3;5). Tọa độ của đỉnh C là: | |||
| (A) (-1;-7) | (B) (2;-2) | (C) (-3;-5) | (D) (1;7) |
| 29. Khẳng định nào trong các khẳng định sau là đúng? | |
(A)
Hai
vectơ
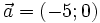 và
và
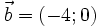 cùng
hướng
cùng
hướng |
(B)
Vectơ
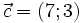 là
vectơ
đối
của
là
vectơ
đối
của
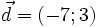 .
. |
(C)
Hai
vectơ
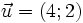 và
và
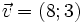 cùng
phương
cùng
phương |
(D)
Hai
vectơ
 và
và
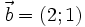 ngược
hướng
ngược
hướng |
30.
Trong
hệ
trục
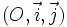 ,
tọa
độ
của
vectơ
,
tọa
độ
của
vectơ
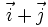 là:
là: |
|||
| (A) (0;1) | (B) (-1;1) | (C) (1;0) | (D) (1;1) |
Tài liệu tham khảo[sửa]
-
Sách
in:
- Hình học 10, Nhà xuất bản giáo dục, 2006, trang 27.
- Hình học 10 Nâng cao, Nhà xuất bản giáo dục, 2006, trang 32.
- Hình học 10, Nhà xuất bản giáo dục, 2001, trang 24.
- Tài liệu giáo khoa thí điểm, Hình học 10, Nhà xuất bản giáo dục,...