Hình học 12/Chuẩn kiến thức và kĩ năng/CTC
| Chủ đề | Mức độ cần đạt | Ghi chú |
|---|---|---|
| 1. Khối đa diện | ||
| 1. Khái niệm về khối đa diện. Khối lăng trụ, khối chóp. Phân chia và lắp ghép các khối đa diện. |
Về
kiến
thức :
Biết khái niệm khối lăng trụ, khối chóp, khối chóp cụt, khối đa diện. |
|
| 2. Giới thiệu khối đa diện đều. |
Về
kiến
thức :
- Biết khái niệm khối đa diện đều. - Biết 3 loại khối đa diện đều : tứ diện đều, lập phương, bát diện đều. |
|
| 3. Khái niệm về thể tích khối đa diện. Thể tích khối hộp chữ nhật. Công thức thể tích khối lăng trụ và khối chóp. |
Về
kiến
thức :
- Biết khái niệm về thể tích khối đa diện. - Biết các công thức tính thể tích các khối lăng trụ và khối chóp. Về kỹ năng : Tính được thể tích khối lăng trụ và khối chóp. |
Ví
dụ.
Cho
hình
chóp
đều
S.ABCD
có
cạnh
đáy
bằng
a,
góc
SAC
bằng
45.
Tính
thể
tích
hình
chóp
S.ABCD.
Ví dụ : Cho khối hộp MNPQM'N'P có thể tích V. Tính thể tích của khối tứ diện P'MNP theo V.
Ví
dụ.
Trên
cạnh
PQ
của
tứ
diện
MNPQ
lấy
điểm
I
sao
cho
|
| 2. Mặt cầu, mặt trụ, mặt nón. | ||
|
1.
Mặt
cầu.
Giao của mặt cầu và mặt phẳng. Mặt phẳng kính, đường tròn lớn. Mặt phẳng tiếp xúc với mặt cầu. Giao của mặt cầu với đường thẳng. Tiếp tuyến của mặt cầu. Công thức tính diện tích mặt cầu. |
Về
kiến
thức :
- Hiểu các khái niệm mặt cầu, mặt phẳng kính, đường tròn lớn, mặt phẳng tiếp xúc với mặt cầu, tiếp tuyến của mặt cầu. - Biết công thức tính diện tích mặt cầu. Về kỹ năng: Tính được diện tích mặt cầu, thể tích khối cầu. |
Ví
dụ.
Một
mặt
cầu
bán
kính
R
đi
qua
8
đỉnh
của
một
hình
lập
phương.
Tính
cạnh
của
hình
lập
phương
đó
theo
R.
Ví dụ. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc SAC bằng 600. Xác định tâm và bán kính mặt cầu đi qua các đỉnh của hình chóp S.ABCD. |
| 2. Khái niệm về mặt tròn xoay. |
Về
kiến
thức :
Biết khái niệm mặt tròn xoay. |
|
| 3. Mặt nón. Giao của mặt nón với mặt phẳng. Diện tích xung quanh của hình nón. |
Về
kiến
thức :
Biết khái niệm mặt nón và công thức tính diện tích xung quanh của hình nón. Về kỹ năng: Tính được diện tích xung quanh của hình nón. |
Ví
dụ.
Cho
một
hình
nón
có
đường
cao
bằng
12cm,
bán
kính
đáy
bằng
16cm.
Tính
diện
tích
xung
quanh
của
hình
nón
đó.
Ví dụ. Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc SAB bằng 300. Tính diện tích xung quanh của hình nón đỉnh O, đáy là hình tròn ngoại tiếp tứ giác ABCD. |
| 4. Mặt trụ. Giao của mặt trụ với mặt phẳng. Diện tích xung quanh của hình trụ. |
Về
kiến
thức :
Biết khái niệm mặt trụ và công thức tính diện tích xung quanh của hình trụ. Về kỹ năng : Tính được diện tích xung quanh của hình trụ. |
Ví dụ. Cắt khối trụ bằng một mặt phẳng qua trục của khối trụ được một hình vuông cạnh a. Tính diện tích xung quanh của khối trụ đó. |
| 3. Phương pháp toạ độ trong không gian | ||
|
1.
Hệ
toạ
độ
trong
không
gian.
Toạ độ của một vectơ. Biểu thức toạ độ của các phép toán vectơ. Toạ độ của điểm. Khoảng cách giữa hai điểm. Phương trình mặt cầu. Tích vô hướng của hai vectơ. |
Về
kiến
thức :
- Biết các khái niệm hệ toạ độ trong không gian, toạ độ của một vectơ, toạ độ của điểm, khoảng cách giữa hai điểm. - Biết phương trình mặt cầu. Về kỹ năng: - Tính được toạ độ của tổng, hiệu, tích vectơ với một số; tính được tích vô hướng của hai vectơ. - Tính được khoảng cách giữa hai điểm có toạ độ cho trước. - Xác định được toạ độ tâm và bán kính của mặt cầu có phương trình cho trước. - Viết được phương trình mặt cầu. |
Ví
dụ.
Xác
định
toạ
độ
tâm
và
bán
kính
của
các
mặt
cầu
có
phương
trình
sau
đây:
a x2 + y2 + z2 - 8x + 2y + 1 = b x2 + y2 + z2 + 4x + 8y - 2z - 4 = Ví dụ. Viết phương trình mặt cầu: a Có đường kính là đoạn thẳng AB với A(1; 2; -3 và B(- 2; 3; 5. b Đi qua bốn điểm O(; ; , A(2; 2; 3, B(1; 2; - 4, C(1; - 3; - 1. |
|
2.
Phương
trình
mặt
phẳng.
Véctơ pháp tuyến của mặt phẳng. Phương trình tổng quát của mặt phẳng. Điều kiện để hai mặt phẳng song song, vuông góc. Khoảng cách từ một điểm đến một mặt phẳng. |
Về
kiến
thức :
- Hiểu được khái niệm véctơ pháp tuyến của mặt phẳng - Biết phương trình tổng quát của mặt phẳng, điều kiện vuông góc hoặc song song của hai mặt phẳng, công thức tính khoảng cách từ một điểm đến một mặt phẳng. Về kỹ năng: - Xác định được véctơ pháp tuyến của mặt phẳng - Biết cách viết phương trình mặt phẳng và tính được khoảng cách từ một điểm đến một mặt phẳng. |
Có
thể
giới
thiệu
tích
có
hướng
của
hai
vectơ
khi
nói
về
vectơ
pháp
tuyến
của
mặt
phẳng.
Ví
dụ.
Cho
Ví dụ. Viết phương trình mặt phẳng đi qua ba điểm A(- 1; 2; 3, B(2; - 4; 3, C(4; 5; 6. Ví dụ. Viết phương trình mặt phẳng đi qua hai điểm A(3; 1; - 1, B(2; - 1; 4 và vuông góc với mặt phẳng 2x - y + 3z - 1 = . Ví dụ. Tính khoảng cách từ điểm A(3; - 4; 5 đến mặt phẳng x + 5y - z + 7 = . |
|
3.
Phương
trình
đường
thẳng.
Phương trình tham số của đường thẳng. Điều kiện để hai đường thẳng chéo nhau, cắt nhau, song song hoặc vuông góc với nhau. |
Về
kiến
thức :
Biết phương trình tham số của đường thẳng, điều kiện để hai đường thẳng chéo nhau, cắt nhau, song song hoặc vuông góc với nhau. Về kỹ năng: - Biết cách viết phương trình tham số của đường thẳng. - Biết cách sử dụng phương trình của hai đường thẳng để xác định vị trí tương đối của hai đường thẳng đó. |
Ví
dụ.
Viết
phương
trình
tham
số
của
đường
thẳng
đi
qua
hai
điểm
A(4;
1;
-
2,
B(2;
-
1;
9.
Ví dụ. Viết phương trình tham số của đường thẳng đi qua điểm A(3; 2; - 1 và song song với đường thẳng
Ví dụ. Xét vị trí tương đối của hai đường thẳng:
d1:
|
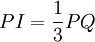 .
Tỉ
số
thể
tích
của
hai
tứ
diện
MNIQ
và
MNIP.
.
Tỉ
số
thể
tích
của
hai
tứ
diện
MNIQ
và
MNIP.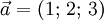 và
và
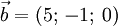 .
Xác
định
vectơ
.
Xác
định
vectơ
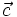 sao
cho
sao
cho
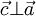 và
và
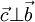
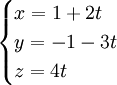
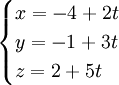 d2:
d2: