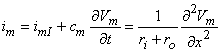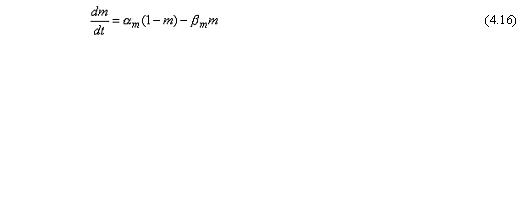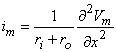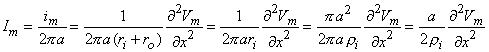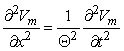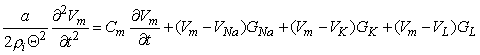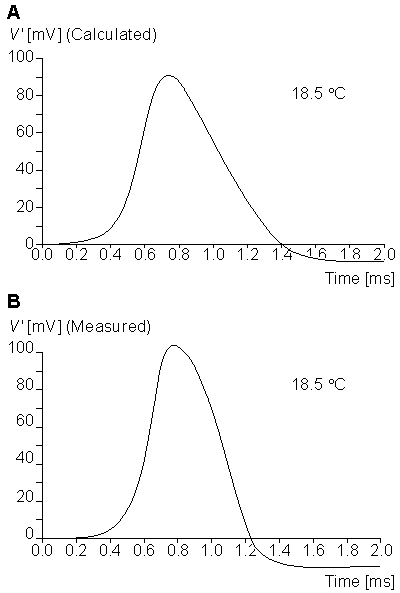Sách:Điện từ sinh học/Phản ứng tích cực của màng tế bào
Phản ứng tích cực của màng tế bào
Mục lục
GIỚI THIỆU.
Khi một xung dòng kích thích được thiết lập để khử cực màng tế bào ở trạng thái nghỉ hoặc vượt quá điện áp ngưỡng, thì màng sẽ đáp ứng lại bằng một xung hoạt động. Để rõ hơn xem hình 2.8 mục 3b và mục 4 “các đáp ứng điện thế hoạt động” tương ứng với các kích thích xuyên ngưỡng(transthreshold) 3 và 4. Đáp ứng được đặc trưng bởi sự tăng lên nhanh chóng của điện thế xuyên màng ban đầu, tới điện thế đỉnh dương và sau đó hồi phục chậm dần về điện áp nghỉ. Phản ứng giai đoạn này xác định xung lực hoạt động.
Phân tích định lượng của xung lực hoạt động đã được thực hiện thành công bởi Alan L.Hodgkin và Andrew F.Huxley và các đồng nghiệp ở Cambridge (Hodgkin and Huxley, 1952abcd). Họ có thể làm được điều này là do hai nhân tố quan trọng. Đầu tiên là sự chọn lựa một sợi axon lớn của mực ống - là sợi thần kinh đường kính của nó khoảng 0,5 mm, và do đó nó đủ lớn để cắm được hai điện cực cần thiết vào môi trường nội bào (Sự ghi nhận việc tìm ra ứng dụng của sợi axon mực ống đối với các nghiên cứu điện sinh lý học được đưa ra bởi J. Z. Young (1936)). Thứ hai là sự phát triển của thiết bị điều khiển hồi tiếp được gọi là kẹp điện áp, có thể giữ điện áp xuyên màng ở bất kì giá trị quy định nào.
Chương này mô tả về thiết bị kẹp điện áp, thí nghiệm của Hodgkin và Huxley, mô hình tính toán học với các số liệu thích hợp gắn với mô hình và mô phỏng kết quả đa dạng về các hiện tượng điện sinh học được công nhận (sự hoạt hóa, sự lan truyền, vân vân…). Phương pháp kẹp điện áp được phát triển riêng bởi K. S. Cole và G.Marmont. Do tầm quan trọng của nó, trước hết ta sẽ tìm hiểu chi tiết nguyên lý của phương pháp kẹp điện áp. Công trình của Hodgkin và Huxley quan trọng không chỉ đối với khả năng định lượng cả màng thụ động và tích cực, nó còn góp phần giúp chúng ta hiểu sâu hơn về cơ chế màng tế bào được nhìn dưới góc độ hoạt động điện sinh học.
Sự cải thiện đáng kể trong việc nghiên cứu điện sinh học màng tế bào do Erwin Neher và Bert Sakmann tiến hành. Năm 1976 họ công bố phương pháp đo dòng ion trong kênh ion đơn (Neher và Sakmann, năm 1976). Phương pháp này được gọi là kẹp ráp nối (patch clamp), là sự phát triển xa hơn của phương pháp kẹp điện áp. Phương pháp kẹp ráp nối cho phép các nhà nghiên cứu khảo sát hoạt động của các kênh đơn ion và các cơ quan nhận cảm và có ứng dụng rộng rãi ví dụ như trong nghiên cứu dược. Bằng cách đo điện dung màng huyết tương nhờ kỹ thuật kẹp ráp nối, nhà nghiên cứu cũng có thể khảo sát được cách điều chỉnh sự thẩm thấu (exocytosis) của tế bào.
Cách vận chuyển điện của màng tế bào sợi trục được thực hiện bởi mạng lưới các dòng ion đi qua một số lượng lớn các kênh ion. Những kênh ion này được vận hành bằng số (xét trong kết quả thí nghiệm kẹp ráp nối); tuy nhiên do số lượng kênh ion lớn nên dòng điện trong một vùng lớn trên màng sợi trục biểu hiện cách xử lý bằng tương tự, xem kết quả nhận được ở một thí nghiệm kẹp điện áp).
Lẽ ra việc thảo luận cách vận chuyển điện qua màng phải được bắt đầu bằng sự nghiên cứu về cách vận chuyển của các kênh đơn ion và tiếp đến giải thích hoạt động điện của màng tế bào bằng việc tổng hợp hoạt động của các kênh ion thành phần của nó, tuy nhiên do lý do lịch sử, ở đây ta thảo luận về cách vận chuyển màng và phương pháp kẹp điện áp trước khi nghiên cứu về cách vận chuyển kênh ion và phương pháp kẹo ráp nối.
PHƯƠNG PHÁP KẸP ĐIỆN ÁP
Mục đích của phép đo kẹp điện áp.
Để mô tả định lượng cơ chế quá trình hoạt hóa, chúng ta phải đo được các dòng ion cấu thành nên dòng màng tổng. Trong mục này, chúng ta mô tả cách hoàn thành việc này bằng phương pháp đo kẹp điện áp.
Các thành phần dòng sau xuất hiện khi sợi thần kinh bị kích thích tại một đầu và điện áp cũng như dòng điện màng của xung truyền trong dây thần kinh được đo ở vùng ngoại biên:
Các dòng điện dọc trục do quá trình truyền xung thần kinh:
Io = tổng dòng điện dọc bên ngoài sợi trục thần kinh
Ii = tổng dòng điện dọc bên trong sợi trục thần kinh
Lưu ý rằng: Io = - Ii
Dòng xuyên màng im trên đơn vị chiều dài có được từ các đặc tính bản thân màng và được liệt kê như sau:
Thành phần dòng điện dung imC trên đơn vị chiều dài Thành phần dòng điện ion imI trên đơn vị chiều dài bao gồm:
- Dòng natri imNa trên đơn vị chiều dài
- Dòng kali imK trên đơn vị chiều dài
- Dòng clo (hay dòng rò) iL trên đơn vị chiều dài
Mục đích của ta là chọn lọc đo được từng dòng ion một, đặc biệt là các dòng Na+ và K+. Chú ý rằng vì ta xét các dòng ion trong suốt quá trình truyền xung thần kinh, nên trở kháng màng (rm) không phải hằng số; nên nó được biểu diễn bằng ký hiệu tượng trưng là biến trở. Bất kì phép đo dòng màng tế bào nào với quá trình truyền xung thần kinh đều cho tổng các dòng này.
Dòng màng tổng (như trong hình 4.1) thỏa mãn phương trình 3.48 mà có thể được viết dưới dạng như sau:
Trong đó:
im = là dòng xuyên màng tổng trên đơn vị chiều dài (µA/cm chiều dài sợi trục)
imI = là thành phần dòng ion xuyên màng trên đơn vị chiều dài (µA/cm chiều dài sợi trục)
cm = là điện dung màng trên đơn vị chiều dài (µF/cm chiều dài sợi trục)
Vm = là điện áp màng (mV)
t = là thời gian (ms)
ri = trở kháng dọc trục nội bào trên đơn vị chiều dài (kΩ/cm chiều dài sợi trục)
ro = là trở kháng kẽ trên một đơn vị độ dài (kΩ/cm chiều dài sợi trục)
x = khoảng cách (cm)
Bằng cách đo Vm(t) và vận tốc quá trình truyền xung Θ, ta có thể tính được Vm(t – x/Θ) và từ đó tìm được im nhờ phương trình 4.1. Mặc dù việc xác định được im là hiển nhiên, nhưng độ chính xác phụ thuộc vào sự đồng nhất của mẫu cũng như sự hiểu biết về các thông số ri, ro, và Θ. Một phương pháp thỏa đáng hơn nữa là dựa trên sự khử các dòng dọc trục.
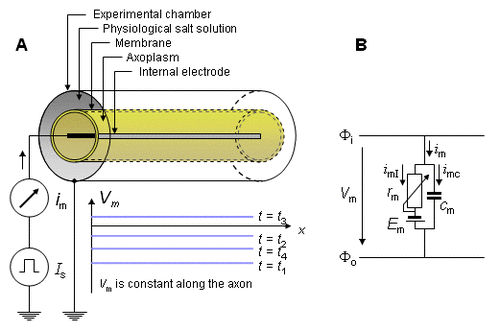
Bằng qui ước điện áp xuyên bào Vm thì điện thế nội bào Φi, và điện thế ngoại bào Φo có quan hệ với nhau: Vm = Φi - Φo. Ngoài ra dòng xuyên bào hướng dương cũng được chọn lựa khi hướng ngoại (đi từ bên trong ra bên ngoài tế bào). Những quy ước này được thể hiện ở phương trình 4.1. Hơn nữa, để duy trì tính nhất quán cách vẽ các mạch điện truyền thống trong các mạch tương đương của màng tế bào, điểm cuối tham chiếu, được chọn để làm điểm đầu cuối mô tả tín hiệu được đo bên ngoài tế bào, làm điểm trên cùng ở bên trong tế bào. Trong những hình vẽ sau minh họa thích hợp cho màng tế bào theo chiều dọc, bên trong màng được định vị bằng mặt bên trái và bên ngoài màng được định vị bằng mặt bên phải của màng tế bào.
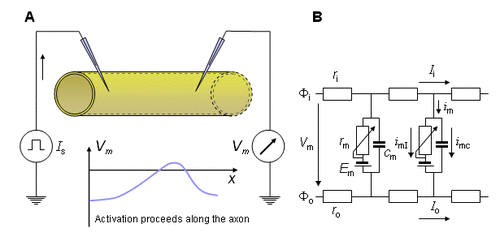
Hình 4.1. Nguyên lý đo dòng điện màng tế bào bằng truyền xung động thần kinh.
(A) Nó được tính toán mà một sóng truyền được bắt đầu ở bên trái và có một vận tốc không đổi ở nơi điện áp được đo. Để nhận được dòng điện xuyên màng ta sử dụng phương trình 4.1; việc thực hiện sẽ yêu cầu đo vận tốc truyền lan vì vậy ²Vm/ x² = (1/Θ²) ²Vm/ t² được ước lượng.
(B) Một phần của phương pháp lõi dây dẫn thẳng (the linear core conductor model), (tính toán giới hạn môi trường ngoại bào) phản ánh phương pháp vật lý trên. (Chú ý rằng chúng ta chỉ xét các dòng ion trong suốt quá trình dẫn truyền xung động thần kinh, trở kháng màng rm không đổi; vì vậy được biểu diễn tượng trưng là biến trở. Để đánh giá nồng độ ion thay đổi theo thời gian do đó Em cũng biến đổi theo thời gian). Các quy ước này được giải thích ở bài này.
Kẹp không gian.
Với thiết bị đo thích hợp có thể kích thích đồng thời toàn bộ chiều dài sợi trục thần kinh. Khi đó điện áp màng tức thời biến đổi đồng nhất dọc theo toàn bộ chiều dài sợi trục thần kinh. Trạng thái này có thể được tạo nên bằng cách lồng vào một điện cực kích thích mỏng dọc theo trục của toàn bộc chiêu dài sợi thần kinh bị cắt ra, trong khi đặt một điện cực khác cùng chiều dài bằng kim loại có hình trụ bao bên ngoài sợi dây thần kinh đó. Điều này làm cho điện thế chỉ có thể thay đổi theo phương bán kính trục, và chỉ phát sinh ra dòng điện tỏa tròn. Hơn nữa, tất cả các nguyên tố màng vận hành đồng thời, vì vậy màng toàn bộ sợi trục thần kinh cũng đồng thời vận hành. Dó đó giữa các điện cực đồng tâm, đo được một dòng điện màng tuân theo phương trình:
Trong đó
im = dòng điện tổng trên đơn vị chiều dài [µA/cm chiều dài sợi trục]
imI = dòng ion tổng trên đơn vị chiều dài [µA/cm chiều dài sợi trục]
cm = điện dung được tạo ra trên đơn vị chiều dài [µF/cm chiều dài sợi trục]
Vì các thiết bị bảo đảm sự đồng đều dọc sợi trục, nó được mô tả là kẹp không gian. Mô hình đo dòng điện bằng kẹp không gian được minh họa trong hình 4.2.
Kẹp điện áp.
Trong phương pháp kẹp không gian, dòng điện màng bao gồm thành phần tụ đóng vai trò như một nguồn dòng gây nhiễu. Thành phần điện dung có thể loại bỏ được bằng cách giữ điện áp màng không đổi trong suốt quá trình đo. Như vậy gọi là phương pháp kẹp điện áp. Do dòng điện dung, trước hết là vế phải phương trình 4.2, tỷ lệ với thời gian phát sinh điện áp, dòng điện dung sẽ bằng không khi điện áp phát sinh bằng không. Trong trường hợp này kết quả phương trình của dòng điện màng giảm là:
im = imI (4.3)
Và dòng điện màng chỉ còn là các dòng ion. (Tiếp theo thời điểm điện áp tăng vọt, một xung dòng ngắn xuất hiện do điện dung của màng. Nó mất đi rất nhanh và không ảnh hưởng đến việc đo các dòng nảy sinh từ sự kích hoạt).
Phương pháp kẹp điện áp được minh họa trong thiết bị kẹp không gian trên hình 4.3. Một nấc điện áp mong muốn phải được chuyển đổi giữa các điện cực bên trong và bên ngoài và dòng chảy giữa các điện cực này được đo (là dòng xuyên màng).
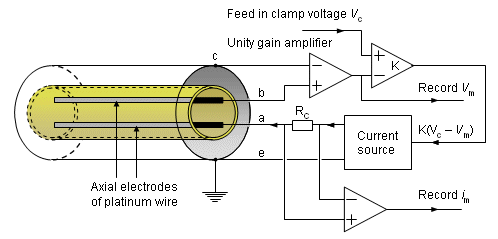
Hiện nay mạch đo kẹp điện áp ở mức độ nào đó phức tạo hơn các phương pháp đã mô tả ở trên và được minh họa trên hình 4.4.
Các điện cực riêng biệt được dùng cho sự ứng dụng dòng điện (a, e) và nhận cảm điện áp (b, c) để tránh các lỗi điện áp do bề mặt điện cực chất điện phân và trở kháng trong dây điện cực dòng mỏng.
Hình 4.4 mô tả nguyên lý mạch đo được thực hiện bởi Hodgkin, Huxley, và Katz (1952). Mạch này gồm có một bộ khuếch đại đồng nhất (có trở kháng vào lớn) mà xác định được điện áp màng ( Vm) giữa bên trong dây thần kinh (b) và bên ngoài dây thần kinh (c).
Đầu ra được đưa tới một bộ cộng, tại đây sự chênh lệch giữa điện áp kẹp (Vc) và điện thế màng đo được (Vm) được xác định và khuếch đại. Đầu ra này, K(Vc - Vm), sẽ hướng tới bộ phát dòng điện. Bộ phát dòng này cung cấp dòng điện cho hệ thống các điện cực (a, e) và vì thế xuyên qua màng. Dòng điện được phát sinh trong suốt quá trình đo điện áp qua một điện trở hiệu chỉnh Rc.
Dòng này được điều chỉnh sao cho điện áp Vm càng tiến gần đến giá trị điện áp Vc, sau đó tín hiệu hồi tiếp được giảm về không. Khi K lớn, sự cân bằng được thiết lập về căn bản Vm = Vc và giữ nguyên giá trị đó. Đây là nguyên lý của hồi tiếp âm và điều khiển tỷ lệ.
Phép đo này được thực hiện với những dây thần kinh có kích thước lớn, đường kính của nó xấp xỉ khoảng 0,05 mm được lồng vào trong hai điện cực mô tả như trên hình 4.4 với dây thần kinh. (Chúng thường được chế tạo là những vòng xoắn ốc đan xen quấn quanh một lõi cách điện).
CÁC VÍ DỤ VỀ KẾT QUẢ THU ĐƯỢC TỪ PHƯƠNG PHÁP KẸP ĐIỆN ÁP.
Kẹp điện áp đối với điện áp Nernst natri.
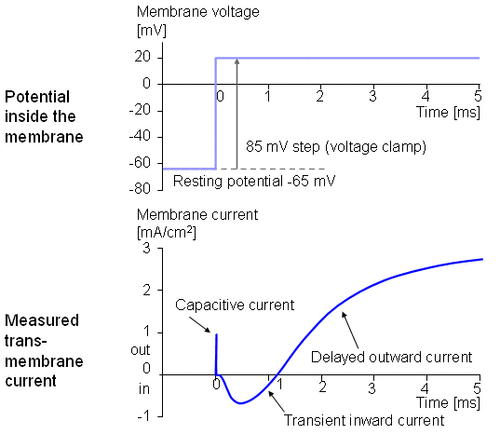
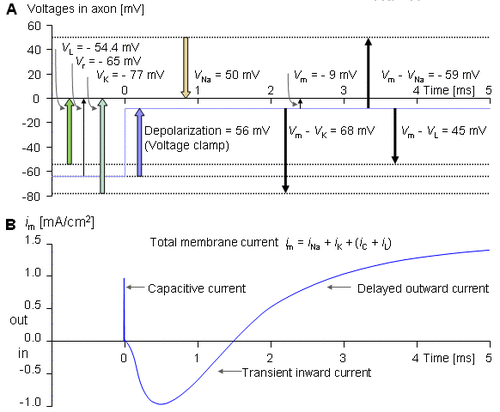
Hình 4.5 mô tả dòng xuyên màng đặc trưng thu được bằng phương pháp kẹp điện áp. Điện thế bên trong màng thay đổi đột ngột từ điện thế nghỉ -65 mV tới +20 mV với bước nhảy là +85 mV. Như vậy, một dòng ion bắt đầu đi vào cơ thể và ra khỏi cơ thể sau khoảng 2 ms và đạt tiệm cận với gí trị 2 mA/cm2.
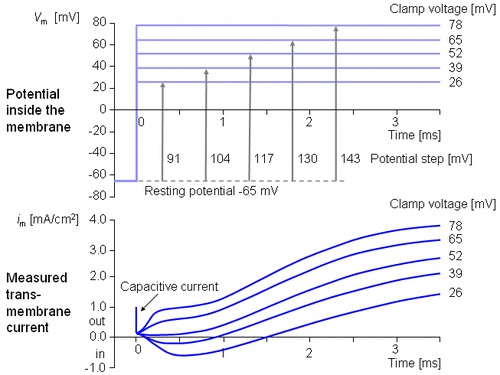
Ta sẽ khảo sát sự xuất hiện dòng điện màng tế bào ứng với các mức điện áp khác nhau. Hình 4.6 cho thấy các kết quả thí nghiệm của 5 phép đo ở các bước điện áp từ 91-143 mV. Trong chuỗi đường cong này cần chú ý dòng điện màng lại được tạo nên bởi hai trạng thái: một trạng thái sớm và một trạng thái muộn như trên hình 4.5.
Dòng sớm có hướng vào phía trong đối với các bước điện áp nhỏ hơn. Khi bước điện áp tăng, biên độ của thành phần hướng vào trong giảm và biến mất hoàn toàn với bước điện áp 117 mV. Với các bước điện áp cao hơn, dòng sớm sẽ hướng ra ngoài và tăng tỷ lệ với bước điện áp. Mặt khác thành phần dòng màng muộn luôn hướng ra ngoài và đơn điệu tăng đến gần một giới hạn tiệm cận nào đó. Giới hạn này sẽ tăng lên khi hàm số của bậc thang điện áp tăng.
Tổng hợp điện áp màng nghỉ -65 mV và bước điện áp 117 mV được kết quả điện áp màng tế bào là +52 mV. Dựa vào nồng độ Na+ ở bên trong và bên ngoài màng, phương trình Nernst ước lượng được một điện áp cân bằng +50 mV. (Chú ý ví dụ trong mục 3.1.3). Vì vậy có thể kết luận rằng thành phần dòng điện sớm được tạo ra bởi các ion Na+ từ đó giảm đúng về 0 ở điện áp cân bằng Na+ và hướng vào trong khi Vm thấp hơn điện áp Nernst Na+ và hướng ra phía ngoài khi Vm lớn hơn điện áp Nernst Na+. Do đó thành phần hướng ra ngoài (thành phần muộn) phải phụ thuộc vào dòng ion K+. Bởi vì Cl- hướng về gần trạng thái cân bằng, nên đối với sợi thần kinh nghỉ thì khi tính thấm của Cl- không tăng trong suốt quá trình điện thế hoạt động dòng Cl- sẽ trở nên rất nhỏ so với Na+ và K+ và có thể bỏ qua.
Sự biến đổi của nồng độ ion.
Một phương thức tiếp cận để chọn lựa đo lường dòng đơn ion Ka+ bằng cách dùng một bước kẹp điện áp tương ứng với điện thế Nernst Na+. Việc này có tác dụng khử dòng Na+. Bằng cách thay đổi có hệ thống nồng độ Na+ ở bên ngoài sợi thần kinh, và sau đó việc lựa chọn bước kẹp điện áp ở điện áp Nernst Na+ tương ứng, chúng ta có thể nghiên cứu được trạng thái đơn K+. Và khi trở lại việc đo dòng dưới điều kiện bình thường (với cả Na+ và K+), trừ dòng K+ còn lại là đơn dòng ion Na+.
Phương pháp này được mô tả ở hình 4.7. Hình này cho thấy kết quả của một thí nghiệm kẹp điện áp được thực hiện đầu tiên trong nước biển thường ở mức điện áp 56 mV. Hình 4.7.A mô tả điện thế Nernst ứng với các ion và các điện áp kẹp khác nhau. Đường cong trên hình 4.7.B diễn tả dòng điện màng tổng được đo bào gồm các dòng thành phần là Na+ và K+. Đường cong (C) là dòng màng được đo sau khi các ion Na+ trong màng đã giảm vì vậy mức điện áp 56 mV đạt tới điện áp mới Nernst Na+. Do đó đường cong này chỉ thể hiện dòng K+. Bằng cách trừ đường cong (C) cho (B) ta được đường cong (D) là dòng màng chỉ của các ion Na+ trong trạng thái ban đầu (Na+ không thay đổi). Các đường cong (C) và (D) là các thành phần mong muốn của (B). Chú ý rằng Hodgkin và Huxley đã giả sử rằng dòng K+ không bị ảnh hưởng bởi sự thay đổi các ion Na+ ở bên ngoài màng vì vậy đường cong (C) sẽ giống nhau đối với cả nước biển thường và nước biển nồng độ Na+ bị giảm bớt.
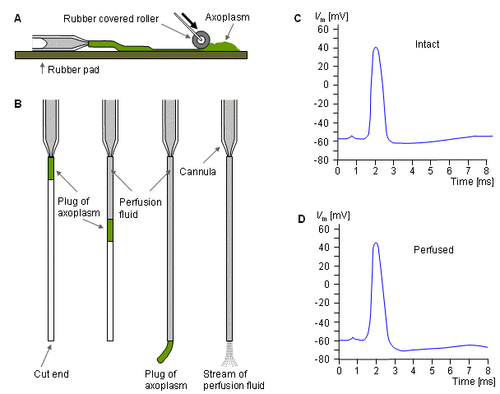
Một kỹ thuật rất thông minh cũng được phát triển bởi Baker, Hodgkin, và Shaw (1962) là cho phép một sự thay đổi để tạo ra các thành phần ion bên trong. Hình 4.8 mô tả cách chuẩn bị sợi thần kinh cho kiểu thí nghiệm của Hodgkin và Huxley. Với thí nghiệm này, đầu tiên là phải ép chặt bào tương ra ngoài; xong xuôi thì sử dụng con lăn (A). Sau đó rót đầy chất dịch lỏng (B) vào sợi trục. Điện thế màng được đo trong suốt quá trình xung lực hoạt động trước khi thực hiện (C) và sau khi thực hiện (D). Các phép đo tiếp theo quá trình hồi phục lại các điều kiện đầu cũng được thực hiện để đảm bảo rằng trạng thái điện của màng tế bào thần kinh không thay đổi.
Sự chặn các kênh ion nhờ các tác nhân hóa dược.
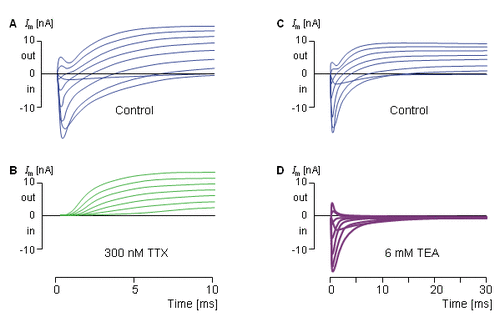
Các dòng ion Na+ và K+ cũng có thể bị tách riêng bằng cách đưa vào các tác nhân hóa dược để chặn chọn lọc các kênh Na+ và K+. Narahashi, Moore và trường đại học của họ cho rằng tetrodotoxin (TTX) chặn có chọn lọc dòng Na+ đi qua màng tế bào (Narahashi, Moore, and Scott, 1964; Moore et al., 1967). Armstrong và Hille (1972) thì cho rằng tetraethylammonium (TEA) sẽ chặn được dòng các ion K+. (Tetrodotoxin là hóa chất độc hại hiện có trong nội tạng của loài cá fugu ở Nhật Bản).
Hình 4.9 cho ta một chuỗi các thí nghiệm kẹp điện áp, bắt đầu ở điều kiện thường. Sau đó các kênh Na+ bị chặn bởi tetrodotoxin, và phép đo chỉ thể hiện dòng của ion K+. Về sau tetrodotoxin được phun ra xa, và một phương pháp điều khiển đo được thực hiện. Tiếp đến là kênh K+ bị chặn bằng tetraethylammonium sẽ cho phép đo chọn lọc được dòng ion Na+ (Hille, 1970).
MÔ HÌNH MÀNG TẾ BÀO HODGKIN-HUXLEY.
Giới thiệu.
Trong phần sau đây, hoạt động của màng tế bào được thảo luận một cách chi tiết, dựa trên mô hình của A.L. Hodgkin và A.F. Huxley (1952d). Mô hình Hodgkin và Huxley dựa trên kết quả của các thí nghiệm kẹp điện áp trên các sợi trục của mực ống. Các mô hình không phải là hình thành từ các nguyên tắc cơ bản nhưng là một sự kết hợp của các lý thuyết và biểu đồ thực nghiệm. Hodgkin và Huxley mô tả công trình của họ như sau:
Mục đích của chúng tôi là tìm ra những phương trình mà mô tả những độ dẫn điện với sự chính xác hợp lý và sự đơn giản một cách đầy đủ cho sự tính toán điện thế tác động . Với tính chất minh họa, chúng tôi sẽ cố gắng cung cấp một cơ sở vật lý cho những phương trình, nhưng phải nhấn mạnh rắng sự giải thích đó không cung cấp bức tranh toàn cảnh màng tế bào.
Mặc dù chỉ là các dạng đơn giản, các mô hình đã giải thích với một độ chính xác đáng kể nhiều đặc tính của màng thần kinh. Đó là mô hình đầu tiên để mô tả cơ sở ion một cách chính xác. Hodgkin và Huxley nhận được giải Nobel năm 1963 nhờ công trình nghiên cứu của họ. Mặc dù bây giờ chúng ta biết trong mô hình Hodgkin-Huxley có nhiều điểm thiếu sót, song đó là điều cần thiết để thảo luận về nó một cách chi tiết để hiểu các hoạt động của màng tế bào và mô hình này.
Bạn đọc cần biết là ban đầu Hodgkin và Huxley viết tài liệu tại thời điểm khi định nghĩa của Vm đã được chọn ngược lại với quy ước được đưa ra vào giữa những năm 1950. Ở đây, chúng tôi sử dụng quy ước hiện nay: Vm là sự chênh lệch điện áp bên ngoài và bên trong màng .
Dòng điện màng tổng hợp và các thành phần của nó.
Hodgkin và Huxley đã nghiên cứu kĩ dòng điện chạy qua màng tế bào trong quá trình hoạt hóa được mô tả trong mô hình vật dẫn song song, mô hình đầu tiên về chuyển động của những ion riêng biệt. Mô hình được minh họa trong hình 4.10, nó bao gồm 4 thành phần dòng điện:
- Dòng tạo bởi các ion Na+
- Dòng tạo bởi các ion K+
- Dòng tạo bởi các ion khác
- Dòng dung kháng
Trong mô hình này, mỗi một thành phần trong số bốn thành phần được giả sử sử dụng cho chính đường dẫn hoặc kênh dẫn của nó. Một chú ý khác theo sau là hướng dương của dòng điện màng tế bào và điện áp Nernst được chọn là từ bên trong ra bên ngoài.
Mô hình được cấu tạo bởi việc sử dụng các thành phần mạch điện cơ bản của nguồn điện áp, điện trở và tụ điện được minh họa trên hình 4.10. Độ thẩm thấu ion của màng tế bào đối với các ion Na+, K+ và độ dẫn điện rò trên một đơn vị diện tích ( dựa theo đình luật Ôm ) như sau:
Trong đó:
GNa, GK, GL: là độ dẫn màng tế bào trên một đơn vị diện tích đối với Na+, K+ và các ion khác ứng với độ dẫn rò ( S/cm2 ).
INa, IK, IL: Dòng điện tạo bởi các ion Na+, K+, và các ion khác (dòng rò) trên một đơn vị diện tích ( mA/cm2 ).
VNa, VK, VL: Điện áp đề cập ở trên được định nghĩa bằng công thức Nernst được xác định bởi công thức Nernt. Và ta có:
Trong đó các chỉ số “i” và “o” chỉ ra nồng độ ion bên trong và bên ngoài màng tế bào tương ứng. Các kí hiệu khác cũng giống như trong trường hợp công thức Nernst và z= 1 đối với Na và K, z= -1 đối với Cl.
Trong hình 4.10 thì các cực tính nguồn áp được chỉ ra có cực tương tự nhau ứng với các giá trị dương. Chúng ta có thể thêm vào cho các điện áp Nernst của Na, K và Cl được tính theo các công thức từ công thức 4.7 đến 4.9 tương ứng với các nguồn áp để chiều điện áp Nernst dương cùng chiều với cực nguồn áp và chiều điện áp Nernst âm ngược lại.
Do nồng độ Clo bên trong rất thấp nên những sự di chuyển của ion Cl- có ảnh hưởng rất lớn tới tỉ số nồng độ Clo. Do đó một luồng nhỏ các ion Cl- sẽ mang đến sự cân bằng điện và Clo không đóng vai trò quan trọng trong việc đánh giá điện thế màng tế bào (Hodgkin và Horowicz, 1959).
Khi Vm = VNa thì nồng độ ion Na+ là ở trạng thái cân bằng và khi đó không có dòng chuyển dời của các ion Na+. Thông thường sự chênh lệch của Vm so với VNa là một phép đo của điện áp hút gây nên dòng Na+. Hệ số liên hệ giữa lực kéo (Vm – VNa) với mật độ dòng của các ion Na+ sẽ được xác định là độ dẫn và nó được xác định theo định luật Ôm.
Bây giờ 4 dòng điện trên có thể được ước lượng cho các điện áp màng tế bào Vm. Các mạch tương ứng được tạo bởi:
- Điện áp Nernst của các ion Na+ và độ dẫn màng tế boa đối với các ion Na+.
- Điện áp Nernst của các ion K+ và độ dẫn màng tế boa đối với các ion K+.
- Điện áp rò ( ngay cả khi dòng rò bằng không do sự chuyển động của các ion Cl- và các ion khác) và độ dẫn điện rò của màng tế bào.
- Điện dung màng tế bào.
Dựa trên cơ sở các nghiên cứu kẹp điện áp, Hodgkin và Huxley đã xác định rằng độ dẫn của màng tế bào đối với các ion Na+ và K+ là các hàm của điện thế truyền màng tế bào và thời gian. Trong khi đó, độ dẫn điện dòng rò lại là hằng số. Dưới kích thích ngưỡng con thì trở kháng màng tế bào và điện dung cũng có thể được coi là hằng số.
Chúng ta phải nhắc lại rằng khi các độ dẫn điện Na và K được tính toán trong suốt quá trình kẹp điện áp thì sự phụ thuộc của chúng vào điện áp được loại bỏ do điện áp trong suốt quá trình đo là hằng số. Tuy nhiên điện áp là một thông số bởi vì nó có thể quan sát được khi nó được so sánh với trạng thái đáp ứng tại các mức điện áp khác nhau. Đối với phương pháp kẹp điện áp thì nó chỉ biến đổi trong khi thực hiện đo đạc theo thời gian mà thôi. Chú ý rằng dòng điện dung là bằng không bởi vì dV/dt=0.
Đối với mô hình Hodgkin- Huxley thì biểu thức đối với mật độ dòng điện truyền màng tế bào tổng là bằng tổng các thành phần dòng dung kháng và ion. Tiếp sau đó mới tính đến các dòng điện của Na, K và dòng rò. Do đó:
Trong đó: Im = Dòng điện màng tế bào trên một đơn vị diện tích ( mA/cm2 ).
Cm = Điện dung màng tế bào trên một đơn vị diện tích ( F/cm2 ).
VNa, VK, VL = Điện áp Nernt đối với Na+, K+ và các ion khác ( mV ).
Vm = Điện áp màng tế bào ( mV ).
GNa, GK, GL= độ dẫn màng tế bào trên một đơn vị diện tích đối với Na+, K+ và các ion khác ứng với độ dẫn rò rỉ (S/cm2 ).
Độ dẫn Kali.
Vì sự biểu diễn độ dẫn Kali trong suốt quá trình thực hiện kẹp điện áp đơn giản hơn so với của độ dẫn Natri nên ta sẽ xét nó trước ở đây.
Hodgkin and Huxley đã nghiên cứu cơ chế độ dẫn ion: [nó] phụ thuộc vào phân bố của những hạt mang điện mà không đóng vai trò những mang trong nghĩa thông thường, nó cho phép những ion đi xuyên qua màng khi nó chiếm những vị trí đặc biệt trong màng. Theo quan điểm này này tốc độ chuyển động (của) những hạt kích hoạt xác định tốc độ mà độ dẫn natri, kali gần tới cực đại nhưng có ảnh hưởng nhỏ về biên độ độ dẫn . (Hodgkin và Huxley, 1952 d, P. 502)
Hodgkin và Huxley đã không thực hiện bất kỳ giả định liên quan đến bản chất của những hạt về mặt hóa học hoặc giải phẫu. Bởi vì vai trò duy nhất của hạt là xác định những phần nhỏ của các kênh trong trạng thái mở, điều này có thể được biểu diễn tương ứng với các biến ngẫu nhiên được xác định bằng xác suất khi kênh được mở.Tuy nhiên, ở đây chúng ta mô tả các mô hình Huxley-Hodgkin vì sẽ tuân theo ý tưởng ban đầu của họ là sự di chuyển hạt trong màng tế bào và điều khiển độ dẫn. (Đây là những tổng kết sau này trong hình 4.13.)
Biến thiên theo thời gian của độ dẫn Kali (GK) phụ thuộc vào kẹp điện áp được biểu diễn trên hình 4.11 kế tiếp nhau và đơn điệu. (Các đường cong trên hình 4.11 trên thực tế đã được xác định nhờ các phương trình Hodgkin-Huxley. Đối với mỗi đường cong, các giá trị hệ số riêng của chúng được liệt kê trong bảng 1 của Hodgkin và Huxley (1952d) đã được sử dụng, vì vậy các số liệu đo được rất sát nhau.) Hodgkin và Huxley lưu ý rằng sự biến thiên này được thỏa mãn bởi một phương tình bậc nhất ở gần cuối của bài, nhưng đầu tiên cần phải có một phương trình bậc ba hoặc bậc bốn. Thật vậy, tính chất này được chứng minh bởi hình dạng xichma của nó, mà đạt được bằng cách giả sử GK tỉ lệ với lũy thừa bốn của độ biến thiên, cũng thỏa mãn phương trình bậc một. Hodgkin và Huxley đã đưa ra những giả thuyết sau cho mô tả toán học và cơ sở vật lý này.
Như đã biết, các ion K+ chỉ đi qua màng tế bào thông qua các kênh kali. Hodgkin và Huxley cho rằng sự đóng mở của các kênh này được điều khiển bởi các phần tử mang điện được gọi là phần tử n. Chúng có thể ở lại một vị trí cho phép (mở) (ví dụ như ở bên trong màng) hoặc ở một vị trí không cho phép (đóng) (ví dụ như ở bên trong màng) và chúng di chuyển giữa những vị trí này bằng những động năng bậc một. Xác suất một phần tử nở trong vị trí mở được biểu diễn bằng thông số n, và trong vị trí đóng là (1 – n), trong đó 0 ≤ n ≤1. Vì vậy khi điện thế màng thay đổi, thì sự phân bố của phần tử n thay đổi và được biểu diễn bằng giá trị xác suất n mới giảm theo hàm mũ.
Trong dạng toán học, những sự biến đổi phụ thuộc thời gian và điện áp của phần tử n giữa các vị trí đóng và mở được biểu diễn bởi sự thay biến đổi của thông số n với các hệ số tốc độ di chuyển phụ thuộc điện áp αn và βn. Điều này dẫn đến sự tương qua bậc nhất sau:
Trong
đó:
αn = hệ số tốc độ di chuyển từ trạng thái đóng sang trạng thái mở của các phần tử n[1/s] βn = hệ số tốc độ di chuyển từ trạng thái mở sang trạng thái đóng của phần tử n [1/s] n = tỷ lệ phần tử n ở trạng thái mở 1 - n = tỷ lệ phần tử n ở trạng thái đóng.
Nếu biết giá trị ban đầu của n, sau đó các giá trị có thể được tính toán bằng việc giải phương trình vi phân:
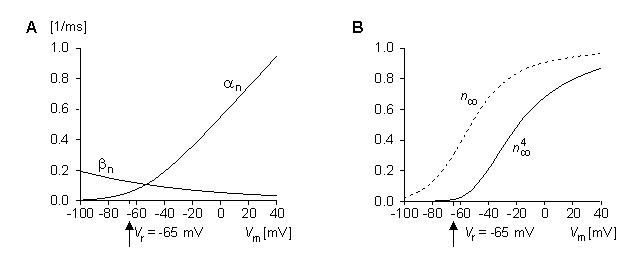
Do đó, tốc độ tăng của tỷ lệ các phần tử n trong trạng thái mở dn/dt phụ thuộc vào tỷ lệ của chúng ở trạng thái đóng (1 - n), tỷ lệ của chúng ở trạng thái đóng và vào hệ số tốc độ di chuyển αn và βn. Bởi lẽ các phần tử nlà các hạt mang điện, nên hệ số tốc độ di chuyển phụ thuộc điện áp nhưng không phụ thuộc vào thời gian. Hình 4.12 biểu diễn sự biến thiên của hệ số tốc độ di chuyển theo điện áp màng. Giải thích các giá trị bằng số của nó ở cuối mục.
Cụ thể hơn, Hodgkin và Huxley cho rằng các kênh kali chỉ được mở ra khi có 4 phần tử n đi ra khỏi vị trí cho phép (bên trong màng) trong một vùng nào đó. Giả sử rằng xác suất của bất kỳ một trong bốn phần tử n ở vị trí cho phép không phụ thuộc vào ba phần tử n còn lại. Khi đó xác suất của kênh ở trạng thái mở bằng xác suất hợp lại của bốn phần tử n này và vì vậy tỷ lệ với n^4. (Những khái niệm này được rút ra dựa vào việc khảo sát các chất nhận acetylcholine, gồm 5 phần tử xung quanh kênh dẫn bằng nước và ở đó một sự di chuyển tổng hợp nhỏ của tất cả các hạt cũng có thể gây đóng hoặc mở kênh (Unwin and Zampighi, 1980).)
Độ dẫn kali trên một đơn vị diện tích là tích của độ dẫn kênh đơn với số kênh được mở. Nếu GKmax là độ dẫn trên đơn vị diện tích khi tất cả các kênh đều mở (nó là giá trị lớn nhất), nếu chỉ có tỷ lệ n^ 4 được mở, ta có:
Trong đó:
GKmax là giá trị lớn nhất của độ dẫn kali [mS/cm²], và n tuân theo phương trình 4.12.
Phương trình 4.12 và 4.13 nằm trong số những biểu thức cơ bản của công thức Hodgkin và Huxley.
Phương trình đối với n trong kẹp điện áp.
Đối với mỗi bước điện áp (kẹp điện áp), thì hệ số tốc độ di chuyển αn và βn hoàn toàn thay đổi thành giá trị khác (nhưng không đổi). Do đó ở một điện áp không đổi, hệ số tốc độ di chuyển trong phương trình 4.12 là hằng số, phương trình vi phân sau có thể được giải đối với n:
Ta
thấy
bước
điện
áp
khởi
đầu
một
sự
thay
đổi
theo
hàm
mũ
đối
với
n
từ
giá
trị
ban
đầu
của
n0
(giá
trị
của
n
tại
t
=
0)
đến
giá
trị
dừng
n∞
(giá
trị
của
n
khi
t
=
∞).
Hình
4.12B
cho
biết
sự
biến
thiên
của
n∞
và
n∞^4
theo
điện
thế
màng.
(B)Biến
thiên
của
n∞
và
n∞^4
là
hàm
của
điện
thế
màng
(GK∞
n^4
).
Tổng kết mô hình Hodgkin-Huxley đối với độ dẫn điện kali.
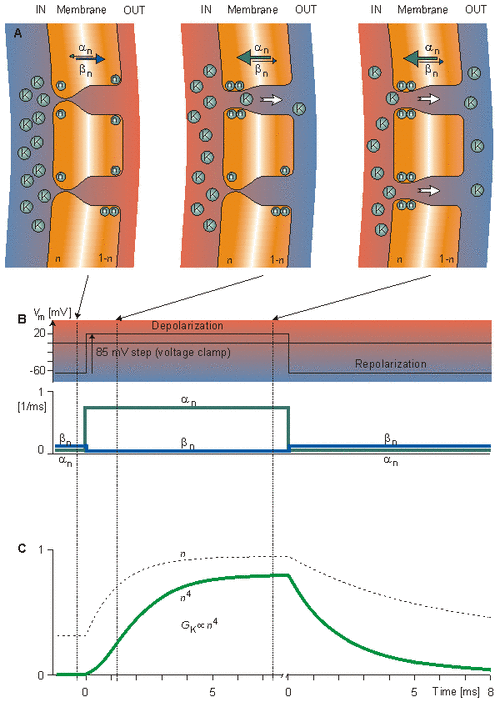
Hình 4.13 minh họa cho các ý tưởng của mô hình Hodgkin-Huxley đối với độ dẫn kali. Trong hình 4.13A đáp ứng của các phần tử n đối với sự khử cực đột ngột được mô tả trước và ở hai thời điểm tức thời kế tiếp nhau trong suốt quá trình khử cực. Ban đầu, tỷ lệ n của phần tử n ở vị trí cho phép ( bên trong màng) là nhỏ, vì αn nhỏ và βn lớn. Vì vậy các kênh kali đều đóng. Sự khử cực tăng αn và giảm βn do đó n tăng theo hàm mũ đến giá trị lớn nhất n. Khi 4 phần tử n chiếm giữ những vị trí xung quanh kênh bên trong màng thì kênh mở ra; vì thế độ dẫn kali GK tỷ lệ với n^4, được chỉ ra ở phương trình 4.13. Hình 4.13A mô tả hiện tượng này trước hết ở một kênh và sau đó là ở hai kênh. Độ lớn của αn và βn được chỉ ra ở hình 4.13A bởi độ dày của mũi tên và ở hình 4.13B bởi các đường cong. Trong hình 4.13C, là đáp ứng của n và n^4 đối với sự khử cực và mô tả sự tái cực.
Bạn đọc có thể kiểm chứng độ dẫn kali tỉ lệ với n^4, bằng cách so sánh đường cong này với đường cong ở hình 4.11 minh họa độ dẫn kali ở khử cực 88 mV (là giá trị mà gần nhất đối với 85 mV được dùng ở hình 4.13). Những đường cong này có dạng gần tương tự nhau.
(A) Sự di chuyển của n-particles giải thích cho sự khử cực đột ngột. Đầu tiên, αn nhỏ và βn lớn được chỉ thị bằng độ dày của các mũi tên. Vì vậy phần n của phần tử n ở trạng thái cho phép (bên trong màng) nhỏ. Sự khử cực tăng αn và giảm βn. Vì vậy n tăng theo hàm mũ tới một giá trị lớn. Khi 4 phần tử n cùng chiếm các vị trí xung quanh kênh bên trong màng, kênh mở ra. (B) Đáp ứng của hệ số tốc độ di chuyển αn và βn đối với khử cực và sự tái cực. (C) Đáp ứng của n và n^4 đối với sự khử cực và tái cực (GK ∞ n4 )
Độ dẫn Natri
Những kết quả mà Hodgkin và Huxley thu được cho độ dẫn Natri trong thí nghiệm kẹp điện áp được minh họa trên hình 4.14 (Hodgkin và Huxley, 1952d). Các đường cong trên hình 4.14 đã được tính toán lại từ phương trình Hodgkin-Huxley và hoàn toàn phù hợp với các số liệu đo được.
Sự biểu diễn độ dẫn Na ban đầu gần tương tự như của K, ngoại trừ tốc độ tăng của độ dẫn trong suốt quá trình khử cực nhanh hơn khoảng 10 lần. Có thể thấy rõ độ dẫn Na tăng trước sự tăng độ dẫn của K. Hodgkin và Huxley lại giả sử rằng các hạt mang điện ở kênh Na được gọi là các phần tử m tồn tại ở các vị trí điều khiển sự mở kênh. Vì vậy chúng có hai trạng thái, mở (cho phép) và đóng (không cho phép); m diễn tả tỷ lệ hạt ở trạng thái mở (ví dụ như ở bên trong màng) và (1 – m) là tỷ lệ hạt ở trạng thái đóng (ví dụ ở bên ngoài màng), trong đó 0 ≤ m ≤1.
Dạng
toán
học
cho
sự
biến
đổi
phụ
thuộc
thời
gian
và
phụ
thuộc
điện
áp
của
các
phần
tử
m
giữa
trạng
thái
mở
và
đóng
cũng
gần
giống
với
K.
Ta
định
nghĩa
những
điều
này
với
ký
hiệu
“m”;
vì
vậy
hệ
số
tốc
độ
truyền
đạt
phụ
thuộc
điện
áp
là
αm
và
βm.
Ta
có
quá
trình
bậc
nhất
sau:
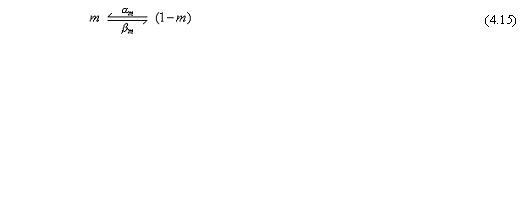
Trong đó:
αm = hệ số tốc độ truyền đạt đối với phần tử m từ trạng thái đóng sang trạng thái mở [1/s]
βm = hệ số tốc độ truyền đạt đối với phần tử m từ trạng thái mở sang trạng thái đóng[1/s]
m= tỷ lệ của phần tử m ở trạng thái mở 1 - m = tỷ lệ của phần tử m ở trạng thái đóng
Một phương trình cho hoạt động của sự hoạt hóa Na có thể được viết giống như cho K, m thỏa mãn quá trình bậc nhất:
Các
hệ
số
tốc
độ
truyền
đạt
αm
và
βm
phụ
thuộc
vào
điện
áp
nhưng
nó
không
phụ
thuộc
vào
thời
gian.
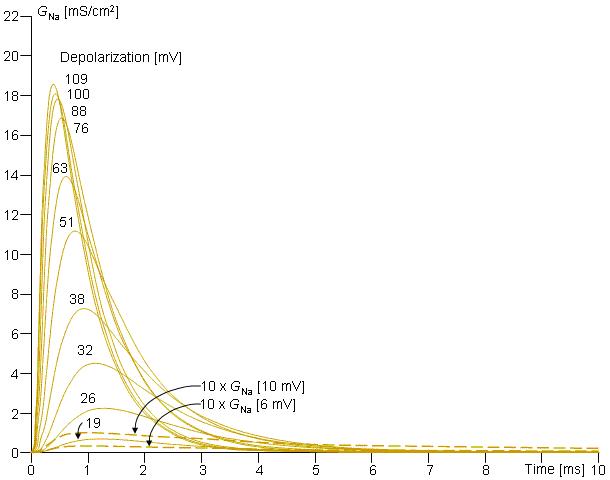
Hình 4.14. Sự biểu diễn độ dẫn Na trong thí nghiệm kẹp điện áp. Điện áp kẹp được diễn tả bằng sự biến đổi từ điện thế nghỉ [mV]. Chú ý độ dẫn Na biến đổi nhỏ ở ngưỡng dưới của sự khử cực và tăng rất nhanh đối với ngưỡng xuyên khử cực (transthreshold depolarization) ( ≥ Vm = 26 mV).
Trên cơ sở hoạt động của phần đầu của đường cong độ dẫn Na, Hodgkin và Huxley cho rằng kênh Na chỉ mở ra khi có 3 phần tử m ở trạng thái cho phép (bên trong màng). Do đó tỷ lệ kênh ở trạng thái mở bằng tỷ lệ mỗi 3 phần tử m ở trạng thái cho phép; vậy nên sự tăng độ dẫn Na ban đầu tỷ lệ với m³.
Sự
khác
nhau
chính
giữa
sự
hoạt
động
của
độ
dẫn
Na
và
K
là
sự
tăng
độ
dẫn
Na
do
sự
khử
cực
màng
tế
bào
không
được
duy
trì.
Hodgkin
và
Huxley
mô
tả
kết
quả
giảm
độ
dẫn
từ
một
quá
trình
khử
hoạt
tính
và
bao
gồm
bằng
việc
đưa
vào
một
phần
tử
h
khử
hoạt
tính.
Thông
số
h
diễn
tả
xác
suất
một
phần
tử
h
ở
trạng
thái
không
khử
hoạt
tính
(mở),
ở
bên
ngoài
màng.
Vì
vậy
(1-h)
là
xác
suất
một
phần
tử
h
ở
trạng
thái
khử
hoạt
tính
(đóng),
bên
trong
màng.
Sự
di
chuyển
của
những
hạt
này
cũng
được
điều
khiển
bởi
các
động
năng
bậc
một:
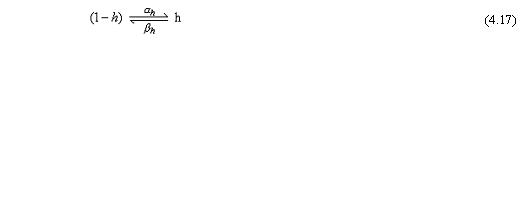
Trong đó: αh là hệ số tốc độ truyền đạt đối với phần tử h từ trạng thái khử hoạt tính sang trạng thái không khử hoạt tính [1/s] βh là hệ số tốc độ truyền đạt đối với phần tử h từ trạng thái không khử hoạt tính sang trạng thái khử hoạt tính [1/s], h là tỷ lệ của phần tử h ở trạng thái khử hoạt tính.
Mặt khác, vì các phần tử h là các hạt mang điện, các hệ số tốc độ truyền đạt αh và βh phụ thuộc điện áp nhưng không phụ thuộc thời gian.
Giả
sử
độ
dẫn
Na
tỷ
lệ
với
số
vị
trí
bên
trong
màng
mà
được
đồng
thời
gắn
3
phần
tử
m
hoạt
hóa
và
không
bị
chặn
bởi
một
phần
tử
h
khử
hoạt.
Do
đó
sự
biến
đổi
độ
dẫn
Na
tỷ
lệ
với
m³h,
và

Trong đó: GNa max là giá tị lớn nhất của độ dẫn Na [mS/cm²], và m thỏa mãn phương trình (4.16) và h thỏa mãn phương trình (4.18).
Tiếp
sau
một
nấc
điện
áp
khử
cực
(kẹp
điện
áp),
m
sẽ
tăng
theo
thời
gian
(từ
m0
đến
m∞)
dựa
trên
biểu
thức
như
phương
trình
4.14
(thay
m
cho
n).
Cách
hoạt
động
của
h
chỉ
là
ngược
lại
vì
trong
trường
hợp
này
nó
sẽ
được
tìm
ra
khi
h0
>>
h∞
và
một
kết
quả
giảm
theo
hàm
mũ
từ
sự
khử
cực.
Vì
vậy
toàn
bộ
các
đáp
ứng
đối
với
mức
điện
áp
khử
cực
bao
gồm
cả
sự
tăng
theo
hàm
mũ
của
m
(sự
tăng
lên
theo
đường
xichma
đối
với
m³)
và
sự
suy
giảm
theo
hàm
mũ
của
h,
vì
vậy
GNa
được
biểu
thị
như
trong
hình
4.19
với
đoạn
đầu
tăng
và
đoạn
sau
giảm.
Cách
hoạt
động
này
là
để
phù
hợp
với
các
dữ
liệu
trong
hình
4.14.
Thêm
vào
đó
ta
quay
trở
lại
giá
trị
lúc
nghỉ
bình
thường
của
m
gần
sát
không,
trong
khi
h
xấp
xỉ
0.6.
Đối
với
trạng
thái
siêu
phân
cực
lúc
đầu
thì
hiệu
ứng
là
để
giảm
m;
tuy
nhiên
vì
nó
rất
nhỏ
nên
sự
suy
giảm
có
thể
xảy
ra.
Đối
với
h
thì
giá
trị
của
nó
tăng
tới
giá
trị
đồng
nhất,
và
ảnh
hưởng
đến
sự
khử
cực
rất
rõ
ràng.
Ảnh
hưởng
này
hoàn
toàn
phù
hợp
với
các
quan
sát
thực
nghiệm.
Hằng
số
thời
gian
đối
với
sự
biến
đổi
h
dài
hơn
đáng
kể
so
với
m
và
n,
có
thể
dẫn
đến
hiện
tượng
“ngắt
dương
cực”,
sẽ
được
nói
đến
ở
phần
cuối
chương
này.
Hình
4.15A
biểu
diễn
sự
thay
đổi
hệ
số
tốc
độ
di
chuyển
αm,
βm,
αh,
và
βh
theo
điện
áp
màng
tế
bào.
Hình
4.15B
biểu
diễn
sự
thay
đổi
của
m∞
,
h∞
,
và
m∞³h∞
theo
điện
áp
màng
tế
bào.
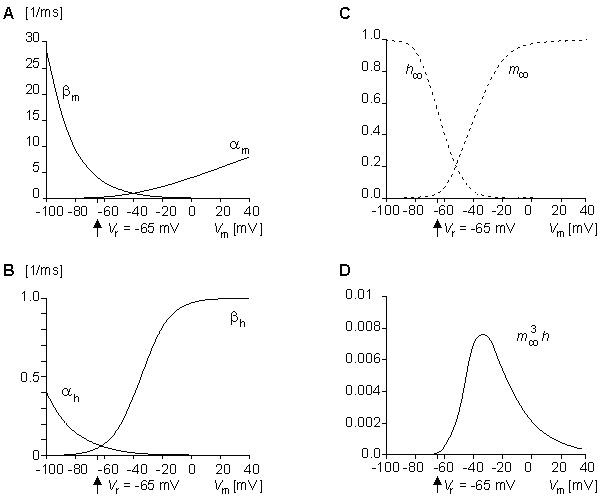
Hình 4.15. Sự thay đổi ở (A) đối với αm và βm, ở (B) đối với αh và βh, (C) m∞ và h∞ , và ở (D) là m∞³h∞ như một hàm số của điện áp. Lưu ý là giá trị của m∞³h∞ nhỏ đến mức độ dẫn Na ở trạng thái ổn định gần như là không.
Tổng kết mô hình Hodgkin-Huxley cho độ dẫn Natri
Tương tự như hình 4.13, hình 4.16 tổng kết cách hoạt động của kẹp điện áp trong mô hình Hodgkin-Huxley nhưng cho độ dẫn Natri. Hình 4.16A biểu diễn đáp ứng của các phần tử m và h theo sự khử cực đột ngột ở trạng thái nghỉ và ở hai khoảng thời gian ngắn nối tiếp nhau trong khi khử cực (Bởi vì các phần tử h có hành vi khử hoạt tính, chúng được vẽ với màu sắc âm bản (nghĩa là, chữ trắng trên một hình tròn đầy ).Ban đầu, tỉ lệ m của các phần tử m trong vị trí cho phép (mặt trong màng ) là nhỏ bởi vì αm nhỏ và βm lớn. Bởi vậy, các kênh Na không mở. Ban đầu, tỉ lệ h của các phần tử h ở vị trí không khử hoạt (kênh mở) (mặt ngoài màng) là lớn bởi vì αh lớn và βh nhỏ. Sự khử cực làm tăng αm và βh, làm giảm βm và αh, như biểu diễn trong hình 4.16A bởi độ dày của những mũi tên và hình 4.16B bởi các đường cong.
Bởi vì hằng số thời gian τm nhỏ hơn τh, m tăng đến một giá trị đồng nhất cực đại nhanh hơn h giảm về không. Cả hai tham số đều tuân theo hàm số mũ (tiếp theo động năng bậc 1) như quan sát trên hình 4.16C. Khi 3 phần tử m xuất hiện tại vị trí xung quanh kênh bên trong màng tế bào và một phần tử h xuất hiện tại vị trí bên ngoài màng tế bào thì kênh mở ra. Do đó ban đầu quá trình tăng độ dẫn của Na, GNa , tỷ lệ với m³ (bởi vì ban đầu h lớn và các phần tử h không khử hoạt chiếm vị trí bên ngoài màng kênh mở.) Trong hình 4.16A, hằng số thời gian ngắn τm được biểu thị bởi sự mở gần như đồng thời của 2 kênh Na. Sau đó, do hằng số thời gian dài hơn là τh, các phần tử h khử hoạt rời khỏi mặt trong của màng, ngăn cản các kênh ion. Do đó, như biểu diễn trong phương trình 4.19, đáp ứng tổng của độ dẫn Na, GNa, tỷ lệ với m³h.
Người
đọc
có
thể
xác
minh
lại
rằng
độ
dẫn
Na
tỷ
lệ
với
m³h
bằng
cách
so
sánh
đường
cong
này
và
đường
cong
trong
hình
4.14,
biểu
diễn
độ
dẫn
Na
khử
cực
ở
88
mV
(
là
giá
trị
gần
85mV
nhất
sử
dụng
trong
hình
4.16)
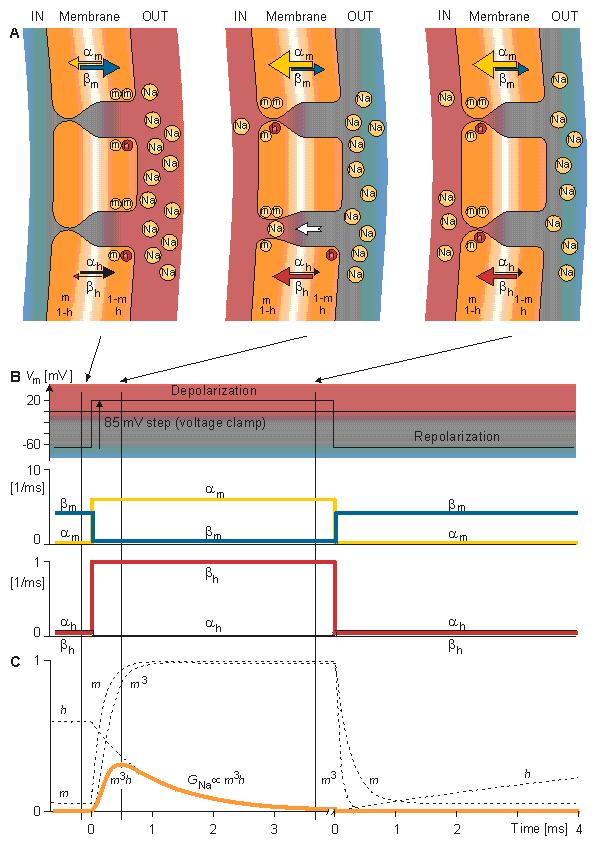
Hình
4.16.
Quá
trình
xác
định
sự
biến
đổi
độ
dẫn
Na
với
sự
khử
cực
và
tái
cực
bằng
kẹp
điện
áp
trong
mô
hình
Hodgkin-Huxley.
(A)Sự
vận
chuyển
của
các
phần
tử
m
và
h
như
một
đáp
ứng
tới
sự
khử
cực
đột
ngột.
Ban
đầu,
αm
nhỏ
và
βm
lớn,
được
biểu
diễn
bởi
độ
dày
của
những
mũi
tên.
Bởi
vậy,
số
các
phần
tử
loại
m
ở
trong
trạng
thái
cho
phép
(mặt
trong
màng)là
nhỏ.
Cũng
như
ban
đầu
giá
trị
của
αh
lớn
và
βh
nhỏ.
Do
đó
các
phần
tử
h
ở
vị
trí
không
khử
hoạt,
mặt
ngoài
màng.
Sự
khử
cực
làm
tăng
αm
và
βh,
làm
giảm
βm
và
αh.
Bởi
vậy
số
phần
tử
m
mặt
trong
màng
tế
bào,
m
,tăng
theo
hàm
số
mũ
tới
mức
đồng
nhất,
và
số
phần
tử
h
mặt
ngoài
màng,
giảm
theo
hàm
số
mũ
về
0.
(B)
Sự
đáp
ứng
của
các
hệ
số
tốc
độ
truyền
đạt
αm,
βm,
αh,
và
βh
tới
sự
khử
cực
và
tái
cực
đột
ngột.
(C)
Đáp
ứng
của
m,h,m³
và
m³h
tới
sự
khử
cực
và
tái
cực
đột
ngột.
Chú
ý
rằng
theo
phương
trình
4.20,
GNa
tỷ
lệ
với
m³h.
Công thức Hodgkin-Huxley
Các hệ số tốc độ truyền đạt.
Hệ số tốc độ truyền đạt α và β của các biến m, n, h được xác định bởi các công thức từ 4.20 đến 4.25. Các công thức này được phát triển bởi Hodgkin – Huxley. Điều này để so sánh với toàn bộ giá trị điện áp kẹp đo được. Đơn vị của hệ số truyền đạt là [1/ms]:

Trong các công thức này thì V'=Vm-Vr, trong đó Vr là điện thế nghỉ. Tất cả các điện áp được tính bằng mV. Vì vậy, V’ là độ lệch giữa điện áp màng và điện áp nghỉ tính theo mV, và nó dương nếu điện thế bên trong màng tế bào thay đổi theo chiều dương (so với bên ngoài). Công thức này giữ cho sợi trục thần kinh của mực ống ở nhiệt độ 6.3 độ C.
Xin lưu ý lại rằng trong bộ thí nghiệm kẹp điện áp, α và β là hằng số bởi điện áp màng được giữ không đổi trong toàn bộ quá trình. Trong suốt quá trình kích hoạt không thực hiện kẹp, nơi điện thế xuyên màng liên tục thay đổi liên tục, các hệ số tốc độ truyền đạt được tính như các công thức ở trên .
Các hằng số
Ngoài các biến được nói ở trên thì các hằng số của mô hình Hodgkin –Huxley cũng được chỉ ra ở đây. Các điện áp được miêu tả trong mối quan hệ với điện áp nghỉ:
Cm = 1 µF/cm²
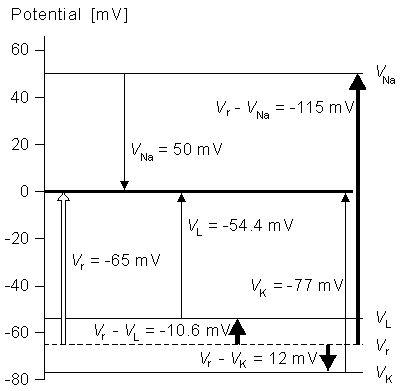
Vr - VNa = -115mV
Vr - VK = +12mV
Vr - VL = -10.613mV
GNa max = 120mS/cm²
GK max = 36mS/cm²
GL = 0.3mS/cm²
Chú ý giá trị điện áp VL không đo được bằng thực nghiệm nhưng chúng được tính toán để dòng bằng không và điện áp màng tế bào bằng điện áp nghỉ. Các điện áp trong sợi trục thần kinh được mô tả ở hình 4.17 bên dưới:
Bảng 4.1.Các công thức Hogkin -Huxley
Truyền xung thần kinh
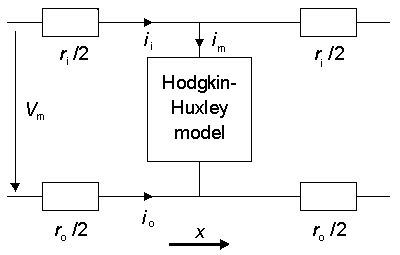
Khi chúng ta thực hiện phân tích quá trình truyền xung thần kinh thay cho các hoạt động không lan truyền (ví dụ khi điện áp màng tế bào nằm trong điều kiện kẹp không gian ) thì chúng ta cần phải quan tâm tới các dòng điện truyền theo hướng trục ngoài các dòng điện truyền của màng tế bào. Chúng ta cùng xem xét ví dụ ở hình 4.18:
Hình trên miêu tả một mô hình cho một đơn vị độ dài của sợi trục thần kinh. Trong mô hình, các giá trị ri và ro biểu diễn các điện trở trên một đơn vị độ dài bên trong và bên ngoài sợi thần kinh tương ứng. Giữa màng tế bào bên trong và bên ngoài, được mô tả như là phản ứng của màng tế bào, chính là mô hình Hodgkin – Huxley. Đối với mạch trong hình chúng ta có:
Trong sợi thần kinh bán kính a, dòng điện màng tế bào trên một đơn vị độ dài là :
im = 2πaIm [μA/ cm] (4.26)
Trong đó : Im là dòng điện màng trên một đơn vị diện tích [μA/ cm2].
Trở kháng chất sợi trục thần kinh trên một đơn vị độ dài là:
Với ρi = Điện trở suất của chất sợ trục thần kinh.
Trong thực tế, khi không gian ngoại bào là rộng lớn, trở kháng bên ngoài trên mỗi đơn vị chiều dài ,ro , là rất nhỏ vì vậy chúng ta có thể bỏ qua chúng. Từ 3.42, 4.26, 4.27 ta có:
Công
thức
4.10
đánh
giá
mật
độ
dòng
qua
màng
tế
bào,
dựa
vào
đặt
tính
thực
của
màng
tế
bào,
trong
khi
đó
Công
thức
4.28
đánh
giá
dòng
qua
màng
tế
bào
dựa
vào
trạng
thái
làm
việc.
Cân
bằng
các
biểu
thức,công
thức
Hodgkin
–Huxley
được
áp
dụng
cho
xung
thần
kinh
được
viết
như
sau:
Dưới các điều kiện trạng thái ổn định thì các xung truyền đi với một tốc độ không đổi và nó duy trì dạng hằng số này. Do đó tuân theo công thức sau:
Với Θ – Tốc độ truyền dẫn [m/s]
Thế 4.30 vào 4.29, công thức mô hình xung thần kinh được viết dưới dạng sau:
Đây là một phương trình vi phân thông thường, có thể giải quyết được về số nếu giá trị Θ đoán được một cách chính xác. Hodgkin và Huxley thu được kết quả từ giải pháp này khá gần so với giá trị đo được (18.8 m/s) .
Với máy tính hiện đại nó là khả thi để giải quyết phương trình vi phân cục bộ thuộc parabon, công thức 4.29, với Vm được coi là một hàm của x và t ( giải quyết khó khăn hơn so với công thức 4.31 ). Giải pháp này cho phép khảo sát Vm từ khi bắt đầu quá trình truyền và kết thúc. Cái mà quan sát được là sự thay đổi về vân tốc và dạng sóng dưới các điều kiện này. Vận tốc trong trường hợp này không có được từ dự đoán ban đầu, nhưng có thể kết luận từ tính toán.
Tốc độ truyền xung thần kinh được tính toán như sau:
Trong đó:
Θ = Tốc độ truyền dẫn [m/s]
K = Hằng số[1/s]
a = Bán kính sợi thần kinh [cm]
ρi = Trở kháng chất sợi trục [Ωcm]
Điều
này
có
thể
được
kết
uận
từ
4.31
với
chú
ý
rằng
công
thức
là
không
đổi
nếu
hệ
số
của
số
hạng
đầu
tiên
được
giữ
không
đổi
(=
1/K
),
nó
được
giả
định
rằng
độ
dẫn
ion
vẫn
không
bị
ảnh
hưởng
(Hodgkin,1954).
Công
thức
4.32
cũng
cho
thấy
rằng
việc
lan
truyền
vận
tốc
của
xung
thần
kinh
là
tỉ
lệ
thuận
với
căn
bậc
hai
của
bán
kính
sợi
trục
thần
kinh
trong
1
sợi
trục
không
bị
myelin
hóa.
Điều
đó
được
chứng
minh
bằng
thực
nghiệm.
Trên
thực
tế
thì
theo
quan
hệ
thống
kê,
tốc
độ
truyền
được
xác
định
như
sau :
Trong đó: d = Đường kính sợi trục thần kinh [m/s]
Vận tốc này trái ngược với quan sát trong sợi trục thần kinh bị myelin hóa, ở đó giá trị vận tốc tỉ lệ nghich với bán kính sợi trục. Một ý kiến về các yếu tố ảnh hưởng tới việc lan truyền vân tốc được đưa ra bởi Jack, Noble và Tsien (1975).
Độ dẫn màng tế bào thay đổi trong thời gian truyền xung thần kinh:
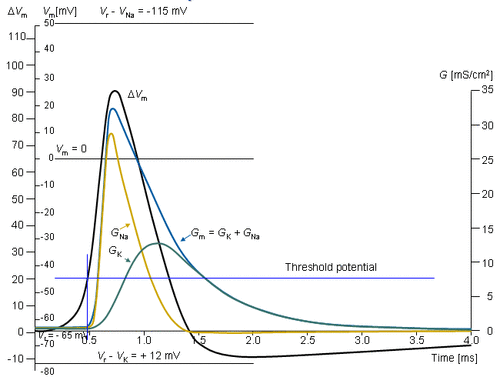
K.S.Cole và H.J.Curtis (1939) chỉ ra rằng trở kháng của màng tế bào giảm rất nhiều trong quá trình hoạt hóa và điều này gần như hoàn toàn là do một sự gia tăng độ dẫn của màng tế bào. Tức là, dung kháng không thay đổi trong quá trình hoạt hóa. Hình 4.19 minh họa các thành phần của độ dẫn màng tế bào, là GNa và GK, và tổng của chúng Gm trong quá trình truyền xung thần kinh và các điện thế màng tế bào tương ứng Vm. Đó là một nghiệm bằng số của công thức 4.31 sau Hodgkin và Huxley ,1952d)...
Thành phần của dòng quan màng tế bào trong quá trình truyền xung thần kinh:
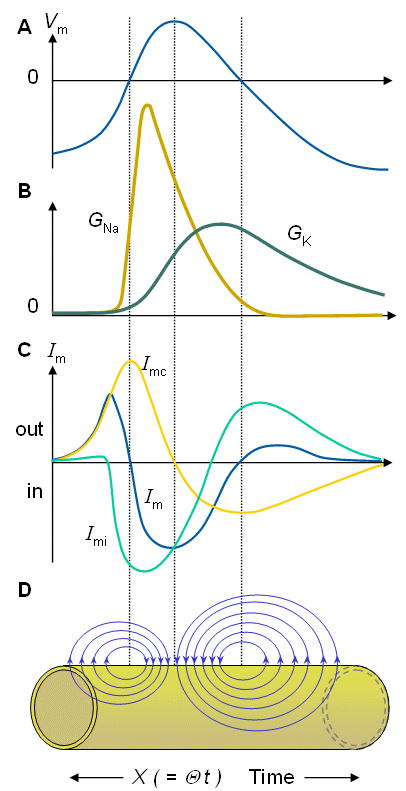
Hình 4.20 mô tả điện áp màng tế bào Vm trong thời gian hoạt động, độ dẫn Natri và Kali ,dòng qua màng tế bào Im cũng như thành phần điện dung và ion ImC và ImI của nó, được miêu tả trong quá trình truyền xung thần kinh (Noble,1966).
Từ hình vẽ tiếp theo có thể cho ta quan sát được:
1. Điện thế bên trong của màng tế bào bắt đầu tăng trước khi độ dẫn natri bắt đầu tăng, bởi vì dòng cục bộ trong mạch điện xuất phát từ gần khu vực hoạt động. Trong giai đoạn này, dòng qua màng tế bào chủ yếu là thành phần điện dung, bởi vì độ dẫn natri và kali vẫn còn thấp.
2. Dòng cục bộ trong mạch khử cực của màng tế bào đến mức mà nó đạt ngưỡng và bắt đầu hoạt hóa.
3. Quá trình hoạt hóa bắt đầu với việc tăng độ dẫn natri. Kết quả là, các ion natri chảy vào trong, gây ra điện áp màng tế bào ít âm hơn và cuối cùng là có điện thế dương.
4. Độ dẫn kali bắt đầu tăng sau đó, thời gian thực hiện chậm hơn so với độ dẫn natri.
5. Khi độ dẫn natri giảm và độ dẫn kali tăng đủ, điện áp màng tế bào đạt đến giá trị tối đa và bắt đầu giảm. Vào lúc này tức (các đỉnh của Vm ), dòng điện dung bằng không (dV/dt =0 ) và dòng điện màng tế bào toàn bộ là dòng ion.
6. Giai đoạn cuối cùng của quá trình hoạt hóa là điều chỉnh độ dẫn kali, thông qua việc thoát ra của dòng kali, làm cho điện áp màng tế bào trở nên âm hơn. Bởi vì độ dẫn kali được nâng lên trên giá trị bình thường của nó, sẽ có một thời điểm khi đó điện áp màng tế bào âm hơn điện áp nghỉ- tức là màng tế bào là siêu phân cực.
7. Cuối cùng, khi các độ dẫn của chúng đạt giá trị nghỉ, điện áp màng tế bào đạt đến điện áp nghỉ.
Các đặc tính của mô hình Hodgkin-Huxley.
Dạng của một xung thần kinh không lan truyền .
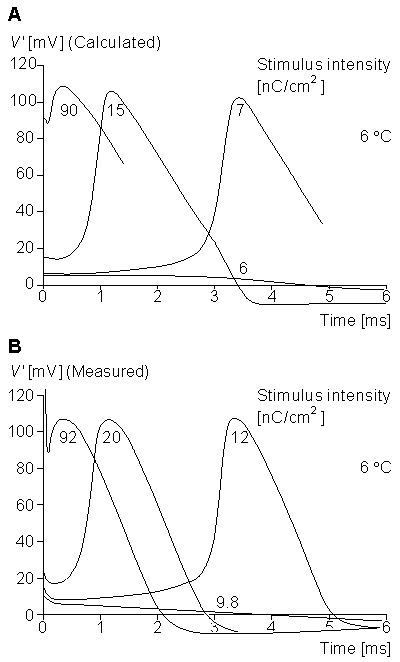
Hình 4.21 chỉ ra các điện thế màng khi được tính ( trên ) và được đo (dưới) tại 6 °C đối với một màng tích cực trong suốt quá trình xung thần thần kinh không lan truyền (kẹp không gian) (Hodgkin and Huxley, 1952d).
Các giá trị trên đường cong tính toán là giá trị trong lời giải của phương trình 4.10. Giá trị trong đường cong này xác định cường độ kích thích và có đơn vị [nC/cm²].
Hiệu ứng nhiệt
Hình 4.22 chỉ ra điện thế màng tại 18,5 ° C tính toán được và điện thế màng đo được tại 20,5 ° C. Cả hai đường có cùng một trục điện áp, nhưng hiệu ứng nhiệt tác dụng trên trục thời gian. Trong trường hợp này, có thể thấy các lỗi giống nhau trong các tính toán điện thế màng như trong trường hợp trước đó. Tuy nhiên, việc hiệu chỉnh tỷ lệ của các hằng số cùng với các hệ số 3.48 đã bảo toàn dạng của đường cong.
Những tác động của nhiệt độ ảnh hưởng tới mô hình vậy cần phải nhân các hệ số của phương trình 4.12, 4.16, 4.18 với hệ số 3^((T - 6. 3)/10). Với T là nhiệt độ ở ° C.
[Hình:0422.gif|thumb|center|500px|Hình 4.22. Điện áp màng tế bào
(A) được tính toán cho giá trị điện áp ban đầu của quá trình khử cực 15 mV tại nhiệt độ 18,5°C
(B) Đo tại nhiệt độ 20.5°C ( Tỷ lệ chia trục Y là như nhau,trục X là khác nhau bởi khoảng nhiệt độ khác nhau).]]
Dạng
của
một
xung
thần
kinh
lan
truyền.
Xung động thần kinh truyền lan tính toán từ phương trình 4.31 tương ứng một cách chính xác so với một xung đo được. Dạng xung động thần kinh truyền lan khi được kích thích được minh họa trong Hình 4.23 (Hodgkin và Huxley, 1952 D). Tương ứng điện áp màng đo tại 18.5 °C được cho trong Hình 4.23B
Chu kỳ trơ :
Mô hình Hodkin-Huxley đồng thời cung cấp dẫn giải cho chu kỳ trơ. Hình 4.17 và 4.18 chỉ ra rằng độ dẫn Kali trở về giá trị tương ứng trạng thái nghỉ chỉ vài phần nghìn giây sau sự khởi đầu của kích hoạt.
Vì sự kích hoạt đòi hỏi natri ( hướng vào trong ) lớn hơn dòng kali (hướng ra ngoài), độ dẫn natri phải đạt đến một giá trị tương đối cao hơn trong thời gian khoảng khôi phục. Điều này cần một kích thích mạnh hơn (mức ngưỡng phải được nâng lên). Khoảng thời gian này được coi như thời kỳ trơ tương đối. Một nhân tố thứ hai à giải thích phản ứng trơ là thực tế theo sau sự khử điện cực tham số khử hoạt tính natri tiếp theo, h ,làm nhỏ lại và khôi phục giá trị nghỉ chậm.
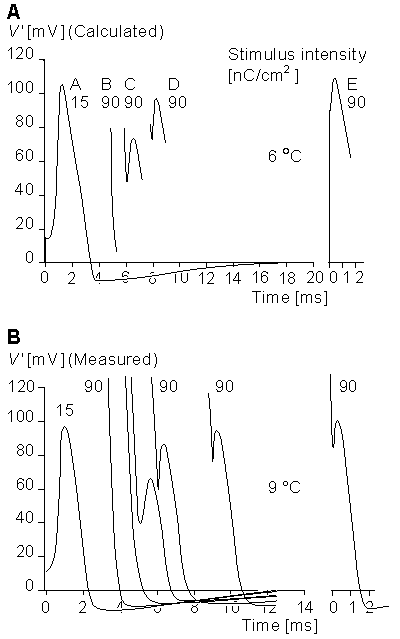
Hình 4 .24 minh họa các đáp ứng được tính toán và được đo đối với kích thích trong quá trình trơ (Hodgkin and Huxley, 1952d). Đường cong 4.24A chỉ ra dáp ứng được tính từ công thức 4.10 tại 6 °C. Sợi trục được kích thích đầu tiên với cường độ 15 nC/cm² và tạo ra xung hoạt động ( đường A trong hình 4.24 A). Sau khoảng 5 ms có sự kích thích khác với cường độ 90 nC/ cm². Vì sợi trục sau xung hoạt động trong trạng thái trơ, nó không tạo ra một xung hoạt động, B đường cong trong Hình 4.24 được tạo ra. Nếu kích thích 90 nC/ cm² được kích thích khoảng 6 ms sau kích thích 15 nC/ cm² đầu , sợi trục tạo một sự kích hoạt, đường cong C, có biên độ thấp hơn so với lần đầu tiên.
Nếu sự kích thích thứ hai xảy ra sau kích thích đầu tiên khoảng 8 ms , thì đáp ứng, đường cong D, gần so với lần đầu tiên . Đường cong E là sự đáp ứng được tính toán với kích thích 90 nC/ cm² khi sợi trục trong trạng thái nghỉ ( Không có xung kích thích 15 nC/ cm² trước đó).
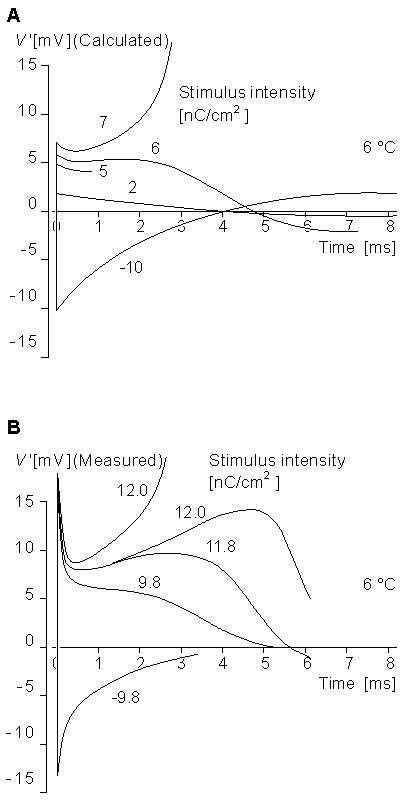
Mức ngưỡng:
Hình 4.25 cho ta thấy mức ngưỡng theo tính toán và đo tại 6 °C với một xung kích ngắn. Tính toán trong phương trình 4.10 cho ta đường cong A. Các giá trị xác định cường độ kích thích [nC/cm²]. Hình vẽ chỉ ra rằng cường độ kích thích ở 6 nC/ cm² hoặc nhỏ hơn hoăc một giá trị âm khoảng -10 nC/cm² không thể tạo xung kích thích trong khi cường độ kích thích là 7 nC/cm² có thể tạo được kích thích. Trong dữ liệu đo thì mức ngưỡng là 12 nC/cm².
Phá vỡ cực dương
Nếu điện thế màng được ưu phân cực với một kích thích mà khoảng thời gian tồn tại lớn hơn mọi hằng số thời gian ion thì khi đó sự ưu phân cực ngay lập kết thúc, màng có thể phát ra một xung hoạt động. Mô hình Hodgkin- Huxley minh họa hiện tượng này và nó được gọi là sự kích thích phá vỡ cực dương (" Sự cố cực dương" -trong nguyên bản). Điều này được mô tả trong Hình 4.26.
Đường cong A là lời giải phương trình 4.10, minh họa điện thế bên trong màng của mô hình khi nó đang âm hơn khoảng 30 mV so với điện thế nghỉ tại 6° C. Trong đường cong B, điện thế nghỉ (của) một tế bào thực tế bào âm hơn 26.5 mV tại 18.5 °C (Hodgkin và Huxley, 1952 D).
Trong mô hình Hodgkin-Huxley, tham số khử hoạt tính tăng từ giá trị thông thường khoảng 0.6 cho tới khoảng 1.0 trong thời gian ưu phân cực .Khi điện áp đạt mức để trở lại giá trị nghỉ, nó tăng lên gây ra tham số kích hoạt Na m tăng . Nhưng phần tử h có thời gian ổn định lớn và có xu hướng vẫn còn ở mức cao.
Một loạt kết quả là độ dẫn Na tăng cao và dòng Na tăng lên, nó có tác dụng kích thích thậm chí tại điện áp nghỉ của màng. Nó cũng liên quan đến độ dẫn Kali (Giá trị trạng thái ổn định của n) được giảm bớt trong thời gian ưu phân cực, và chỉ phục hồi với một khoảng thời gian tương ứng với thời gian sự khử hoạt natri.
4.4.8 Tính đúng đắn của mô hình Hodgkin-Huxley .
Mô hình Hodgkin – Huxley là mô hình màng tế bào không bao gồm các giả định sau: 1. Hình dạng, biên độ và ngưỡng của điện áp màng trong thời gian kích thích như là hàm của nhiệt độ . 2. Hình dạng, biên độ và tốc độ xung thần kinh lan truyền. 3. Sự thay đổi,dạng và biên độ trở kháng màng trong thời gian hoạt hóa. 4. Tổng dòng chảy natri đi vào và kali đi ra trong thời gian hoạt hóa. 5. Ngưỡng và đáp ứng trong thời thời kỳ trơ. 6. Biên độ và dạng của đáp ứng ngưỡng con. 7. Đáp ứng phá vỡ cực dương . 8. Thích ứng.
Trên cơ sở thực tế trong chương này, mô hình Hodgkin- Huxley là mô hình lý thuyết quan trọng nhất mô tả màng tế bào kích thích.
Phương pháp kẹp miếng
Giới thiệu
Để làm rõ một kênh ion hoạt động như thế nào thì cần kiểm tra các yếu tố ảnh hưởng đến việc đóng mở kênh cũng như đo lượng dòng. Đôi khi, những khó khăn chính là việc cô lập một vùng diện tích màng rất nhỏ chứa đúng một vài (hoặc độc nhất) kênh ion, và việc đo lường những dòng ion rất nhỏ.
Hai nhà sinh lý học tế bào, Edwin Neher và Bert Sakman của Viện Max Planck (Gottingen, Đức) đã thành công trong việc phát triển một kỹ thuật cho phép họ đo dòng màng của một kênh ion đơn lẻ. Họ đã sử dụng một vi điện cực bằng kính , gọi là micropipette, có đường kính loại 1 µm. Người ta nói rằng do tình cờ họ đã đặt điện cực rất gần với màng tế bào đến mức mà nó liên kết chặt chẽ với màng tế bào. Trở kháng của mạch đo sau đó lên đến khoảng 50 GΩ (Neher và Sakman, 1976). Sự thay đổi được dòng gây ra bởi những kênh ion đơn lẻ của tế bào có thể được đo bằng phương pháp kẹp điện áp. Thiết bị này được biết đến như là một “kẹp miếng” bởi vì nó kiểm tra hoạt động của một “miếng” màng; nó tạo thành một cấu hình “kẹp không gian” rất tốt.
Phương pháp kẹp miếng đã được phát triển cao hơn để đo điện dung của màng tế bào (Neher và Marty,1982). Vì điện dung màng tỉ lệ theo bề mặt màng nên việc kiểm tra những thay đổi nhỏ trong diện tích bề mặt màng có thể thực hiện được. Đặc trưng này đã chứng tỏ được sự hữu ích trong nghiên cứu quá trình kích thích bài tiết. Các tế bào thần kinh, cũng như các tế bào sản xuất hoocmon và các tế bào bảo vệ (giống như các tế bào lớn), sản sinh ra các chất khác nhau. Chúng được tích trữ trong các bọc bao quanh màng. Khi tế bào bị kích thích, các bọc di chuyển tới bề mặt tế bào. Màng tế bào và bọc chảy ra, và các chất được giải phóng. Tế bào lớn sản sinh ra hixtamin và các chất làm tăng phản ứng kích thích cục bộ khác. Các tế bào lõi tuyến thượng thận giải phóng hoocmon adrenalin (hoocmon stress) và các tế bào bêta trong tuyến tụy giải phóng insulin. Neher đã làm sáng tỏ các các quá trình kích thích bài tiết trong những loại tế bào này thông qua sự phát triển của kỹ thuật mới giúp ghi lại sự kết hợp của các bọc với màng tế bào. Neher đã nhận thức rõ rằng những tính chất điện của một tế bào sẽ thay đổi nếu diện tích bề mặt của nó tăng lên, do đó nó có thể ghi lại quá trình kích thích bài tiết thực tế. Thông qua việc phát triển cao hơn nữa thiết bị tinh vi này, với độ phân giải cao nó cho phép ghi lại sự kết hợp của từng bọc với màng tế bào. Năm 1991, Neher và Sakman đã được nhận giải Nobel cho công trình của họ.
Kỹ thuật đo kẹp miếng
Phần này chúng ta thảo luận về nguyên lý của kỹ thuật đo kẹp miếng (Sakman và Neher,1984; Neher và Sakman, 1991). Chúng ta không trình bày các chi tiết kỹ thuật vì chúng đã có trong tài liệu gốc (Hamill et al .1981;Sakman và Neher, 1984).
Có bốn phương pháp chính :
1. Cell-attached recording
2. Whole cell recording
3. Outside-out configuration
4. Inside-out configuration
Bốn
cấu
hình
này
được
minh
họa
rõ
hơn
trong
hình
4.27
và
được
thảo
luận
chi
tiết
hơn
ở
phần
dưới.
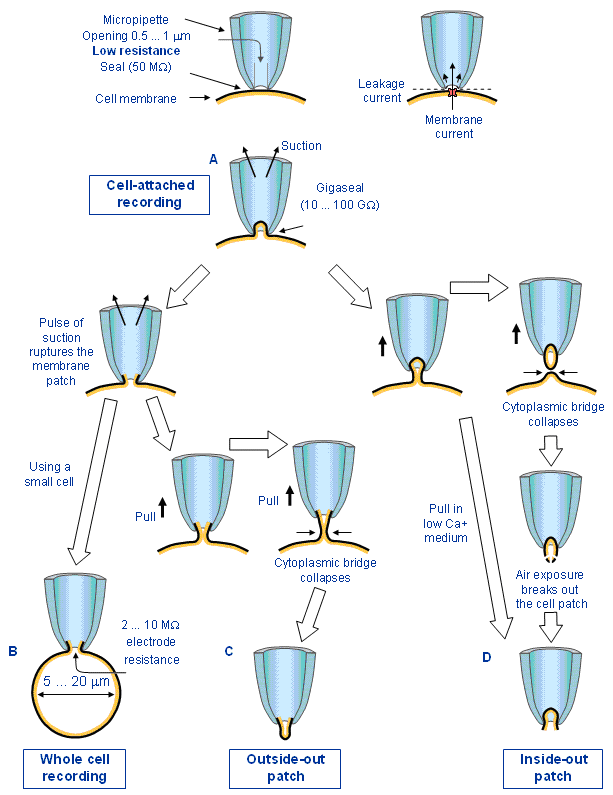
Hình 4.27. Biểu đồ minh họa 4 phương pháp kẹp điểm khác nhau (A) cell-attached recording, (B) whole cell configuration, (C) outside-out configuration, and (D) inside-out configuration. (Chỉnh sửa từ Hamill et al., 1981.)
Nếu một vi điện cực kính được đánh bóng bằng nhiệt, gọi là một micropipette, có một đầu mở khoảng 0,5-1 µm được đưa vào tiếp xúc rất khít với 1 màng tế bào đã được làm sạch enzym, nó tạo thành một miếng bịt (seal) loại 50 MΩ .Mặc dù trở kháng này là khá cao, trong phạm vi kích thước của micropipette miếng bịt rất lỏng lẻo, và dòng chảy qua micropipette bao gồm những dòng rò đi vào quanh miếng bịt (tức là những dòng mà không chảy xuyên qua màng ) và che đi những dòng xuyên màng kênh ion mong muốn ( rất nhỏ).
Nếu một lực hút nhỏ được đặt vào micropipette,miếng bịt có thể được tăng lên theo hệ số khoảng 100-1000. Điện trở qua miếng bịt là 10-100 GΩ. Miếng bịt này, gọi là “gigaseal”, làm giảm bớt dòng rò tới điểm nhọn, nơi mà nó có thể đo đươc các tín hiệu mong muốn- những dòng ion qua màng trong diện tích của micropipette.
Cell-attached recording
Trong hình thức cơ bản của cell-attached recording, micropipette được đưa vào tiếp xúc với màng tế bào, và một miếng bịt kín được tạo bởi sự hút vùng ngoại vi của lỗ micropipette, như mô tả ở trên. Sự hút thường được giảm đi khi miếng bịt được hình thành, nhưng tất cả dòng micropipette đã được loại bỏ ngoại trừ những dòng chảy qua chỗ màng đã mô tả. Kết quả là sự trao đổi ion giữa trong và ngoài micropipette chỉ có thể xảy ra qua các kênh ion nằm trong đoạn màng. Xét các kích thước nhỏ, chỉ có rất ít kênh có thể nằm trong miếng màng đang quan sát. Khi một kênh ion đơn lẻ mở ra, các ion di chuyển qua kênh; những sự dịch chuyển này tạo thành dòng điện, vì các ion mang các hạt mang điện.
Whole cell recording
Trong whole cell recording, màng tế bào trong phạm vi micropipette ở phương pháp cell-attached recording bị đứt với một nhịp hút ngắn. Bây giờ micropipette được gắn kết trực tiếp vào bên trong của tế bào, trong khi gigaseal vẫn được duy trì. Vì vậy nó ngăn chặn các dòng rò. Ngược lại điện trở điện ở trong khoảng 2-10 MΩ. Ở trạng thái này các vi điện cực đo dòng tổng của các kênh ion của toàn bộ tế bào. Trong thời gian mà gigaseal được giữ nguyên, trạng thái này tương tự với một sự thâm nhập vi điện tử thường. Kỹ thuật có thể được áp dụng chuyên biệt cho các tế bào nhỏ có đường kính trong khoảng 5-20 µm và tạo ra các bản ghi tốt trong những tế bào nhỏ như những tế bào hồng cầu.
Outside-out configuration
Outside-out configuration là một phương pháp gần giống với whole cell recording. Trong phương pháp này, sau khi màng tế bào bị đứt với một nhịp hút, micropipette được kéo ra khỏi tế bào. Trong quá trình rút ra, một cầu nối tế bào chất bao quanh bởi màng được kéo ra trước tiên từ tế bào. Chiếc cầu này ngày càng trở nên hẹp hơn cũng như sự chia tách giữa micropipette và tế bào tăng lên, cho đến khi nó bị gãy, để lại đằng sau một tế bào nguyên vẹn và một miếng nhỏ màng bị cô lập và gắn với phần cuối của micropipette. Kết quả là một miếng màng được gắn vào, trong đó, mặt ngoài tế bào ở bên ngoài và mặt trong tế bào ở bên trong micropipette. Với phương pháp này, có thể thấy được mặt ngoài của màng tế bào với các dung dịch “tắm” khác nhau. Do vậy nó có thể sử dụng để nghiên cứu tỉ mỉ hoạt động của các kênh ion đơn lẻ được hoạt hóa bởi các receptor ngoại bào.
Inside-out configuration
Trong phương pháp inside-out configuration, micropipette được kéo từ trạng thái cell-attached mà không đứt màng với một nhịp hút. Cũng như phương pháp outside-out trong quá trình rút ra, một cầu nối tế bào chất bao quanh bởi màng bị kéo ra khỏi tế bào. Chiếc cầu này ngày càng trở nên hẹp hơn và cuối cùng bị gãy, tạo thành một cấu trúc khép kín bên trong pipette. Cái túi này không thích hợp cho các phép đo điện. Tuy nhiên phần màng ở bên ngoài pipette có thể bị bẻ gãy khi tiếp xúc một thời gian ngắn với không khí, và do đó mặt phẳng tế bào chất của màng bị hở ra ngoài (chỉ là đảo ngược của outside-out configuration). Các miếng inside-out cũng có thể thu được mà không tiếp xúc trực tiếp với không khí nếu việc rút ra được thực hiện trong môi trường Canxi tự do. Với cấu hình này, bằng cách thay đổi mật độ ion trong dung dịch “tắm”, ta có thể kiểm tra hiệu quả của việc thay đổi nhanh mật độ trên mặt phẳng tế bào chất của màng. Do vậy phương pháp này có thể được sử dụng để nghiên cứu sự điều chỉnh tế bào chất của các kênh ion.
Sự hình thành của một miếng outside-out hay inside-out có thể kéo theo sự sắp xếp lại cấu trúc chính của màng. Những ảnh hưởng của sự cách ly các đặc tính của kênh đã được xác định trong một số trường hợp.
Những ứng dụng của phương pháp kẹp miếng
Từ 4 kỹ thuật kẹp miếng, phương pháp cell-attached configuration làm xáo trộn ít nhất cấu trúc và môi trường của màng tế bào. Phương pháp này cung cấp một phép phân tích dòng theo một vài bậc của độ lớn có phạm vi rộng hơn các phương pháp đo dòng trước đây. Điện thế màng tế bào có thể được thay đổi mà không cần các vi điện cực nội bào. Cả kênh truyền hoạt hóa và điện thế hoạt hóa đều có thể được nghiên cứu trong môi trường ion bình thường. Hình 4.28 biểu diễn bản ghi dòng điện rò của một kênh ion đơn lẻ tại bản cuối cơ thần kinh của sợi cơ ếch.
Trong phương pháp whole cell configuration, một đường dẫn nhỏ có điện trở rất thấp (2-10 MΩ) được hình thành giữa micropipette và mặt trong tế bào. Khi phương pháp này áp dụng cho các tế bào lớn, nó giúp nhà nghiên cứu đo dòng và điện thế màng, cũng như các phương pháp vi điện cực thường làm. Nhưng khi áp dụng cho các tế bào rất nhỏ, nó cung cấp và thêm vào các điều kiện để có thể thực hiện các phép đo điện thế miếng chất lượng cao. Các bản ghi điện áp miếng có thể được hoàn thành với phương pháp toàn tế bào cho những tế bào nhỏ như tế bào hồng cầu. Nhiều loại tế bào khác có thể được nghiên cứu điện áp miếng với các điều kiện đầu theo cách này. Trong đó là các tế bào nhuộm crom nặng, các tế bào nút tâm nhĩ cô lập ở tim thỏ, các tế bào tuyến tụy, các tế bào tim nuôi sinh mới và các tế bào hạch có lông.
Một tế bào nhuộm crom đường kính 10 µm có thể đáp ứng để minh họa các thông số điện có thể gặp. Tế bào này có điện thế đầu vào ở trạng thái nghỉ là vài GΩ và dòng hoạt động khoảng vài trăm pA. Nếu điện cực có điện trở nối tiếp Rs khoảng 5 MΩ , thì nó đại diện cho một điện trở nối tiếp không đáng kể trong cấu hình phép đo. Điện dung màng Cm khoảng 5 pF do đó hằng số thời gian τm = RS•Cm khoảng 25 µs. Do vậy phép đo một điện áp miếng có thể được thực hiện đơn giản bằng cách đặt một điện áp vào micropipette và đo dòng điện theo quy ước.
Outside-out configuration là một phương pháp đặc biệt phù hợp cho những thí nghiệm kiểm tra các kênh ion được điều khiển bởi các receptor ngoại bào. Dung dịch ngoại bào có thể được biến đổi dễ dàng, cho phép kiểm tra ảnh hưởng của các chất truyền khác nhau, hoặc sự thấm các ion. Cấu hình này đã được sử dụng để đo sự phụ thuộc của độ dẫn kênh AChR trong những tế bào mới hình thành trên ion thấm. Những miếng outside-out cũng đã được sử dụng để cách ly cổng truyền các kênh Cl- trong màng của các thân nơ-ron dây cột sống, trong nơ-ron Aplysia và trong màng cơ của Ascaris
Inside-out configuration là phương pháp thích hợp cho những thí nghiệm nghiên cứu ảnh hưởng của thành phần nội bào của các kênh ion. Việc điều khiển thành phần dung dịch trên cả hai mặt của màng đã có thể thực hiện trong quá khứ nhưng với những kỹ thuật khá phức tạp, phương pháp kẹp miếng với inside-out configuration là cách đơn giản để đạt được mục đích này. Hầu hết những nghiên cứu cho đến nay đều có liên quan đến vai trò của Ca2+ nội bào. Cấu hình này cũng đã được sử dụng cho những nghiên cứu tính thấm , và cho việc làm lộ ra bề mặt trong của các màng dễ bị kích thích điện tới các tác nhân loại bỏ kênh Na+ không hoạt động.
QUAN ĐIỂM HIỆN ĐẠI VỀ CÁC KÊNH ION
Giới thiệu
Mặc dù mô hình Hodgkin – Huxly được công bố từ 40 năm trước, nhưng theo nhiều phương diện, nó vẫn thỏa mãn về định lượng và cấu trúc lý thuyết của nó. Những biểu thức Hodgkin – Huxley nhận được từ 1 loạt các thí nghiệm để đo tổng và thành phần dòn ion của màng tế bào của sợi thần kinh. Để thu được dữ liệu có trong các dòng ion này thì khái niệm kẹp không gian và kẹp điện áp được đưa ra giới thiệu. Kẹp điện áp loại bỏ dòng điện dung, còn kẹp không gian loại bỏ các dòng gây nhiễu khác xung quanh trục. Số lượng đã đo được là tổng dòng của 1 màng tế bào vĩ mô đặc biệt mà khi đi qua đó nó gây ra mật độ dòng ion. Vì kết quả là lượng hợp nhất nên nó cho mở kênh hoạt động của các nguyên tố màng tế bào riêng rẽ để từ đó hình thành nên dòng tổng.
Hodgkin – Huxlay đã nhận thấy màng tế bào chính là 1 lớp lipid có hằng số chất điện môi vào khoảng 5 và có điện trở suất 2×10^9 Ωcm, và là 1 chất cách điện cực kỳ tốt. Hai giả thuyết được đưa ra để giải thích các dòng ion chuyển qua là 1 chất trung gian, giống như 1 chất mang các chất cần vận chuyển, và 1 dòng đi qua các kênh. Hodgkin và Huxley không chỉ ra sự khác biệt giữa 2 khả năng này, dù trong trang tài liệu cuối ( Hodgkin và Huxley , 1952, trang 502) họ đã không ghi rằng hình thức rõ ràng nhất về giả thuyết chất mang đã đối lập với sự theo dõi của họ.
Đến thời điểm này , các nhà nghiên cứu vẫn đang nghiên cứu về Protein màng tế bào, rằng có quá nhiều protein màng tế bào, tốc độ chảy qua vượt quá 10^6 ion/1 kênh trong 1 giây. Mặc dù các protein này vẫn được nghiên cứu tỉ mỉ bằng rất nhiều kĩ thuật nhưng cấu trúc của chúng vẫn chưa được xác định rõ ràng, tuy nhiên, có nhiều nét đặc biệt, có cả sự có mặt của kênh nước, điều này là hoàn toàn dễ hiểu .Trong phần còn lại của bài này, chúng tôi sẽ miêu tả 1 vài thông tin về cấu trúc và chức năng. Đây chỉ là những giới thiệu ngắn gọn và chỉ để mở đầu, bạn đọc muốn tìm hiểu kĩ hãy tìm cuốn Các vật liệu mở rộng của Hill 1992.
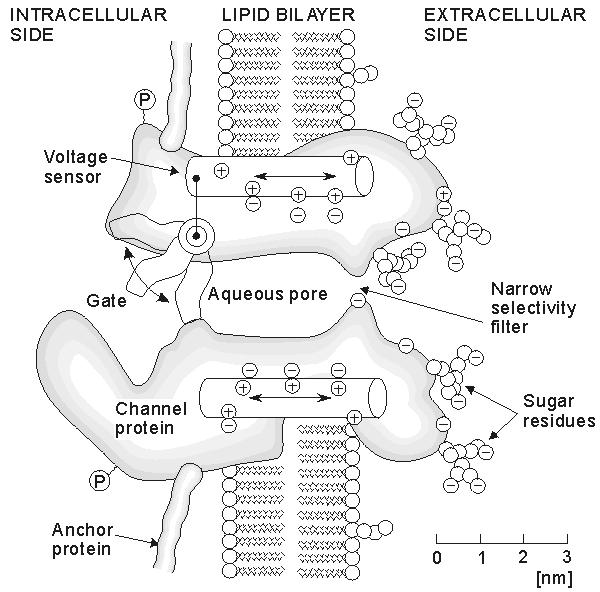
Hình 4.29 . Giả thuyết làm việc cho 1 kênh. Kênh bị kéo dãn ra như 1 đại phân tử xuyên màng với 1 lỗ nằm chính giữa. Vùng chức năng– giống như 1 bộ lọc có lựa chọn. Cổng và cảm biến– được suy ra từ các cuộc thí nghiệm về kẹp điện áp và bắt đầu được ghi trên hình vẽ bởi các nghiên cứu cấu trúc ( Redrawn của Hille 1992)
Trước khi bắt đầu, xin giới thiệu những khái niệm chung về kênh protein ( minh họa trên hình 4.29 ). Mặc dù dựa trên những công nhận về các đặc điểm đặc trưng của kênh, tuy nhiên hình vẽ chỉ là “ Giả thuyết về sự làm việc “ . Nó chứa 1 dạng bản mẫu xác định các thông số vật lý điện tử quan trọng kết hợp giữa “ tính chọn lọc “ và “ cổng( GATING ) “, sẽ được so sánh ngay sau đây. Kích thước thông thường của 1 protein có đường kính khoảng 8 nm và dài 12 nm ( gồm có 1800 – 4000 amino axit được sắp xếp trong 1 hoặc 1 vài chuỗi Polypeptit ). Chiều dài thực sự của nó vượt quá độ dày của lớp lipid kép vì vậy chỉ có 1 phần nhỏ của phân tử protein nằm trong màng. Điều cực kì quan trọng cho các nhà nghiên cứu đó là khả năng phân biệt giữa cấu trúc các protein nằm trong màng ( tức là, phần kị nước ) với thành phần nằm ngoài màng( tức là, phần thấm nước ngoài màng tế bào và các nguyên tố tế bào chất). Chúng ta có thể thấy rằng điện áp màng yêu cầu là 0.1 V , các giá trị này tăng đến khi điện màng tế bào đạt 10^6 V/m. Trường có cường độ này có thể tác dụng 1 lực lớn vào các chất có trong màng tế bào, như hình 4.29 chỉ ra, và nó cũng làm cho sự thay đổi hình dạng theo sự khử cực màng tế bào. ( Sự thay đổi hình thù này làm thay đổi thay đổi độ dẫn của khe thấm nước (aqueous pore )). Thêm vào đó còn có, dòng ion chảy qua kênh nước, có thể ảnh hưởng bởi các điện tích cố định dọc theo bề mặt lỗ.
Cách hoạt động của kênh đơn
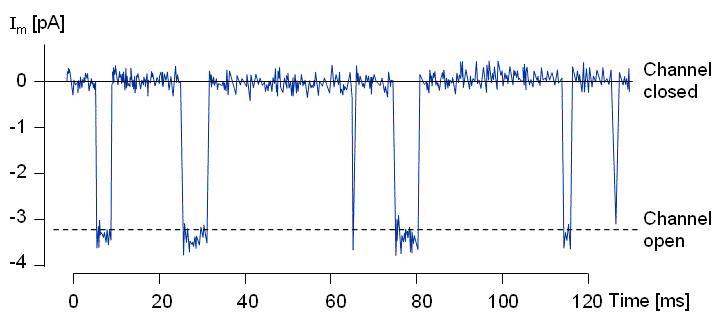
Như đã nói, chúng ta biết rằng protein màng tế bào hỗ trợ cho dòng chảy ion chứa trong khe đã được điền đầy nước hoặc các kênh mà qua đó dòng ion chảy qua. Ứng dụng của kĩ thuật kẹp miếng là tạo khả năng quan sát hoạt động của kênh đơn dễ dàng hơn. Về mặt này, nhiều nghiên cứu đưa ra rằng các kênh này chỉ có 2 trạng thái: hoặc là mở hoàn toàn hoặc là đóng hoàn toàn ( Những phép đo này được thực hiện bởi Hodgkin- Huxley có thể giải thích như sự phát sinh từ hoạt động ở mức không gian trung bình của rất nhiều các kênh đơn lẻ).
Thực tế, hầu hết các kênh thực sự tồn tại ở 3 trạng thái mà được miêu tả theo chức năng như sau :
Nghỉ
ngơi
Hoạt
động
Không
hoạt
động
.
Một ví dụ đó là kênh Natri, đã được đề cập ngay từ đầu trong chương này. Ở mức độ kênh đơn lẻ, mức ngưỡng truyền sẽ thay đổi cùng với điện thế xuyên màng làm tăng khả năng để mở kênh đã đóng. Sau quá trình mở kênh 1 thời gian, kênh lại bị đóng lại giống như kết quả của 1 quá trình mới của kênh- quá trình khử hoạt. Mặc dù quá trình khử hoạt tính của kênh Kali trong sợi trục thần kinh của mực ống đã không được theo dõi và kiểm tra, nhưng những thông tin mới về kênh đơn lẻ đạt được từ kênh Kali Shaker từ loài ruồi giấm đen – loài tuân theo các quy luật chung ở trên. Thực tế, sự chuẩn bị này đã được sử dụng để kiểm tra hoạt động cơ học của quá trình khử hoạt. Vì vậy có thể thấy tuơng đối tổng thể của các kênh đơn.
Kênh Ion
Có nhiều kiểu kênh, nhưng tất cả đều có 2 đặc tính quan trọng chung : mở cổng( GATING ) và tính thấm có lựa chọn. Mở cổng tức là mở và đóng kênh, phụ thuộc vào sự có mặt “các lực” bên ngoài tác động mà các kênh chia làm 2 lớp chính:(1) kênh ligand-gated, điều chỉnh luồng phát xung thần kinh ( ví dụ, kênh nhạy với chất kolin axetylen có ở khớp nối cơ thần kinh.) và (2) kênh voltage-gated , kênh này đáp ứng với các chất điện phân ( ví dụ: Natri, Kali, Canxi ). Nét đặc trưng thứ 2 là tính thấm có chọn lọc. Nó mô tả khả năng của 1 kênh cho phép chỉ 1 kiểu dòng ion đi qua( hoặc có thể là 1 họ của ion đó ).
Chất độc tố thần kinh có khả năng chặn những kênh đặc biệt, chất độc tố thần kinh là công cụ quan trọng trong khi nghiên cứu protein màng tế bào. Chất độc tố thần kinh đầu tiên được sử dụng theo cách này là Tetrodotoxin (TTX ) ( xem phần 4.3.3), một chất có tính chọn lọc cao và ức chế mạnh đối với độ dẫn kênh Natri. Vì vậy TTX có thể ngăn ( khử hoạt ) dòng natri một cách có lựa chọn từ dòng ion tổng, nó rất hiệu quả trong các nghiên cứu để xác định các thành phần dòng ion đơn lẻ qua màng tế bào. Thực ra TTX ngăn cản với riêng luồng Natri và cũng làm tăng sự ủng hộ với quan điểm cho rằng các ion natri chỉ đi qua các kênh natri đặc biệt. Bằng cách sử dụng một lượng bão hòa chất toxin đánh dấu phóng xạ, người ta đánh giá mật độ kênh. ( Với Natri, mật độ kênh khá thưa 5- 500 / µm² màng ). Những chất toxin đánh dấu cũng rất hữu ích trong việc làm sạch các kênh chuẩn bị, tạo nên các nghiên cứu cấu trúc hợp lý.
Bây giờ chúng ta mô tả ngắn gọn 3 phương pháp kĩ thuật sử dụng để giải thích cho cấu trúc kênh (1) lý sinh, (2) sinh học phân tử, (3) vi điện tử và nhiễu xạ điện tử . Mặc dù đã có một cái nhìn phù hợp, nhưng vẫn còn nhiều điều là tự suy diễn, cho nên cần có một hình ảnh chính xác thể hiện cấu trúc kênh chính xác hơn.
Cấu trúc kênh : Phương pháp Lý sinh
Các phương trình Hodgkin – Huxley đưa ra những mô phỏng chính xác dưới nhiều điều kiện khác nhau, những phương trình này đã được giới thiệu trong những phần đầu của chương và được tổng kết trong mục 4.4.3 và 4.4.4. Hodgkin và Huxley xem xét các yếu tố vật lý liên quan đối với các kết quả thu được từ các phương trình này. Vì vậy, các biến m, n và h, được cho là các thông số lý thuyết, được hiểu như là để thể hiện các số lượng vật lý thực và vì vậy chúng giải thích cho các phần tử điện tích trong màng tế bào - được tìm thấy ở trong hoặc ở ngoài bề mặt và là yêu cầu để mở hoặc đóng các kênh màng tế bào. Những giải thích cụ thể của các phương trình Hodgkin- Huxley đã được giới thiệu ở phần đầu trong chương này. Tuy Hodgkin và Huxley quan tâm tới giới hạn của nghiên cứu này ( Hodgkin và Huxley , 1952 ) :” Các đặc điểm đặc biệt trong các phương trình của chúng tôi là những giải thích vật lý, nhưng thành công của các phương trình của chúng tôi là không có bằng chứng về sự thay đổi cơ cấu thấm nước nào cả khiến chúng tôi phải thay đổi suy nghĩ trong quá trình đưa ra các công thức này .”
Hình 4.30 và 4.31 chỉ ra quá trình phản ứng của một kênh đơn lẻ có đáp ứng với kẹp điện áp; hình 4.30 chỉ ra rằng đáp ứng của kênh Natri đối với quá trình khử cực ở 40mV; trong khi hình 4.31 lại chỉ ra đáp ứng của kênh Kali của sợi trục thần kinh của mực ống trong dải điện áp từ -100 mV đến 50 mV. Nếu bỏ qua tác động của nhiễu, thì rõ ràng kênh là điều kiện dẫn hoặc không dẫn. ( Thực ra, mặc dù quá trình chuyển trạng thái là hoàn toàn ngẫu nhiên, nhưng các nghiên cứu cẩn thận đã chỉ ra rằng quá trình đóng và mở là đột ngột trong tất cả mọi trường hợp ). Mức điện áp trung bình của 40 phép thử liên tiếp, đưa ra trong hình 4.30, có thể giải thích như là dòng điện tổng từ 40 kênh Natri cùng hoạt động một lúc ( cho rằng các kênh hoạt động độc lập thống kê với nhau ). Cái thứ hai tiếp cận cái được đo trong một quá trình Hodgkin- Huxley với một số lượng lớn các kênh được đo đồng thời. Những quan sát tương tự được áp dụng đối với kênh Kali minh họa trên hình 4.31. Các giá trị trung bình cho thấy nó giống như dữ liệu của kẹp điện áp Hodgkin- Huxley.
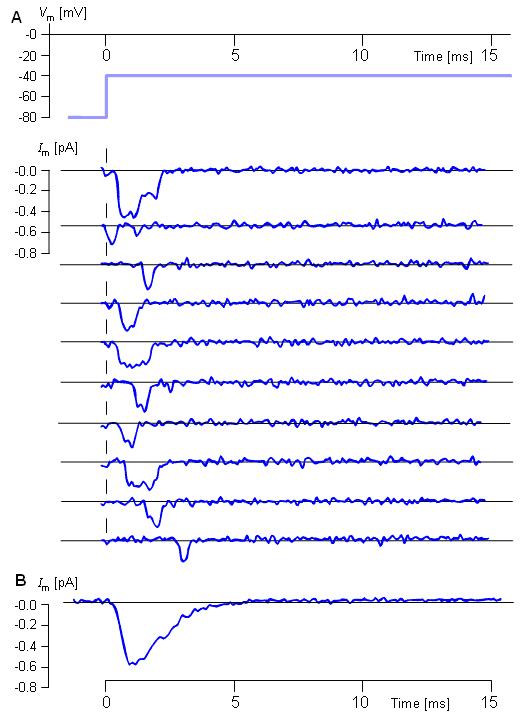
Hình 4.30. Mở cổng của các kênh Natri đơn lẻ. Quá trình ghi lại kẹp miếng của riêng dòng natri trong cơ ngón chân cái của chuột trưởng thành trong bước điện áp -80 đến -40 mV.
-
- (A) lấy 10 thử nghiệm liên tục lọc ở dải thông 3 KHz. Hai kênh mở đồng thời xuất hiện trong bản ghi đầu tiên, kẹp miếng chứa hơn 10 kênh Natri. Đường cắt ngang cho thấy mức độ dòng khi tất cả các kênh đều đóng ( dòng nền).
-
- (B) Đường tổng cộng đó là của 352 phép lặp của cùng 1 phương thức. T = 15 °C. ( Từ Hille, 1992, cung cấp bởi J. B. Patlak; xem Patlak và Ortiz, 1986.).
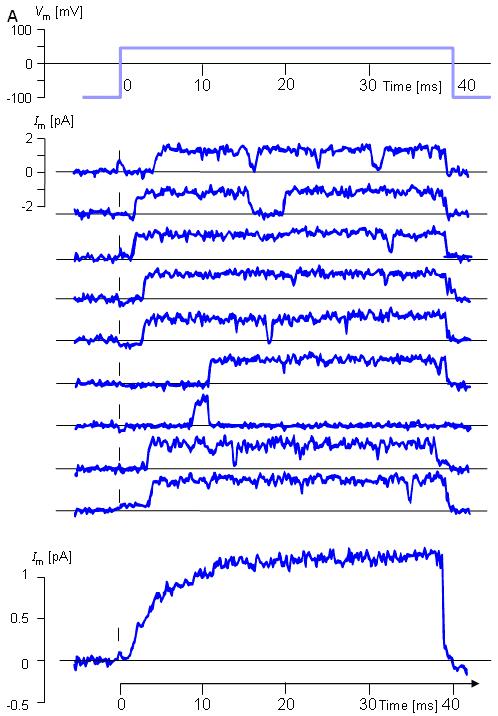
Hình 4.31. Mở cổng của các kênh Kali đơn lẻ: ghi lại kẹp miếng của riêng dòng Kali trong sợi trục thần kinh của mực ống với bước điện áp từ -100 mV đến 50 mV.
-
- (A) Chín thử nghiệm đã cho thấy độ dẫn của kênh ở 20 –pS khi lọc ở băng thông 2 –KHz.
-
- (B) Đường tổng chung của 40 phép thử . T = 20 °C. ( Từ Hille, 1992, dựa trên dữ liệu từ Bezanilla F và Augustine CK, 1986.).
Hoạt
động
của
kênh
đơn
được
miêu
tả
trên
hình
4.31
đã
chứng
minh
tính
ngẫu
nhiên
của
việc
đóng
mở
kênh
đơn
lẻ.
Phù
hợp
với
mô
hình
Hodgkin
–
Huxley
đã
được
trình
bày
là
Kênh
Kali
này
có
xác
suất
n^4
khi
mở
.
Nếu
GKmax
là
độ
dẫn
khi
tất
cả
các
kênh
đều
mở,
khi
đó
độ
dẫn
dưới
các
điều
kiện
khác
là
GK
=
GKmax•(n^4).
Và
tất
nhiên
điều
này
phù
hợp
với
phương
trình
(4.13)
của
Hodgkin
–
Huxley
đã
khẳng
định.
Có thể giải thích n như là phản ánh của 2 khả năng: (1) 1 đơn vị con của kênh Kali được mở và (2) có 4 đơn vị con như vậy, mỗi cái phải được đặt trong điều kiện mở của chính kênh đó. Hodgkin và Huxley đưa ra các khả năng đặc biệt này từ các yêu cầu về sự tồn tại của Mở cổng các phần tử nhỏ giống như 1 mô hình vật lý hợp lý. Các Phần tử nhỏ này chưa từng được định nghĩa giống như “ kênh Protein ” mà như chúng ta đã biết là có chứa các “nguyên tố điện tích ” . ( xem hình 4.29 ). Mặc dù quan niệm về toàn thể các điện tử trung tính ( electroneutrality, có thể thỏa đáng hơn khi mô tả nó giống như nguyên tố lưỡng cực. Ứng dụng của trường khử cực trong sự sắp xếp các lưỡng cực này gây ra chuyển động ( ví dụ như sự thay đổi hình dáng) có khả năng để mở hoặc đóng các cổng kênh. Với sự thêm vào, như chuyển động lưỡng cực chẳng hạn, trong thực tế, nó thiết lập 1 dòng điện dung đóng mở -dòng này được thêm vào để kết hợp với sự dịch chuyển của các điện tích ở bên ngoài và bên trong màng tế bào. Nếu trường tác dụng tăng lên từ từ , đạt đến 1 điểm cuối cùng tại đó tất cả các lưỡng cực được liên kết thành 1 trường và dòng đóng mở đạt giá trị cao nhất ( Bão hòa ) . Ngược lại ,, dòng liên kết với các điện tích lưu trữ ở bên trong hay bên ngoài bê mặt màng là không giới hạn, và cũng tăng tuyến tính với điện áp xuyên màng đặt vào. Bởi vì các đặc tính khác nhau này mà các phép đo với 2 kẹp điện áp khác nhau nhiều có thê được sử dụng để tách riêng biệt 2 thành phần và cho dòng mở cổng của chúng. ( Bezanilla,1986).
Cấu trúc kênh : nghiên cứu về di truyền học phân tử
Trong những năm gần đây, phương pháp vô tính gen đã được sử dụng trong những nghiên cứu về cấu trúc kênh được thiết kế để xác định chuỗi amino acid bậc 1 trong protein kênh. Người ta có thể kiểm tra xem có phải tế bào tạo protein theo cách thông thường hay không khi đựoc cung cấp một đoạn thông tin hay gen vô tính. Noãn bào của loài cóc châu Phi Xenopus Laevis thường được dùng để kiểm tra những biểu thức giả định về kênh mRNA. Các kênh kết quả có thể được sử dụng "kẹp miếng" và các đặc tính mở cổng theo điện áp hay ligand được kiểm tra để khẳng định chắc chắn liệu potein tổng hợp có thực sự là protein kênh mong muốn.
Mặc dù cấu trúc bậc 1 của nhiêu kênh hiện nay đã xác định được nhưng những quy luật để suy luận ra cấu trúc bậc 2 và cấu trúc bậc 3 vẫn chưa được tìm ra. Tuy nhiên các phỏng đoán về tạo hình dạng cho một chuỗi protein đã được tiến hành. Một nghiên cứu gần đây xoay quanh tính có thể kéo giãn của 20 hoặc của các amino acid kỵ nước vì điều này có thể mở rộng qua màng tế bào và biểu hiện các hoạt động tương đương trong màng tế bào( intralipid). Theo cách này , chuỗi thẳng amino acid có thể chuyển đối sang một chuỗi có các vòng và các nếp dựa vào các cị trí phần chia của phân tử nằm bên trong màng, bên trong tế bào chất , và không gian bên ngoài tế bào chất( ngoại bào). Khả năng co giãn tính sợ nước của chuỗi aminoacid chuyển sang màng tế bào có thể cung cấp các chỉ dẫn về cấu trúc và vùng ranh giới giữa các vùng dẫn ion, cũng như là vị trí của các nhóm điện tích mà liên quan tới sự chuyện động của các điện tích mở cổng nhận cảm điện áp.
Cách tiếp cận này rất thành công trong việc nghiên cứu quá trình khử họat ion Kali bằng phương pháp sàng lắc. Sau quá trình hoạt hóa, quá trình khử hoạt xảy ra tiếp theo không phụ thuộc vào điện áp. Do đó có thể suy ra rằng quá trình khử hoạt phải xảy ra bên ngoài màng tế bào, ngoài ra nó còn phải chịu ảnh hưởng của điện trường màng tế bào. Vì lý do này cũng như các lý do khác mà vùng các amino –cuối cùng trong vùng tế bào chất của phân tử protein màng tế bào đã được nghiên cứu bởi việc xây dựng nên " đột biến loại bỏ" ( deletion mutant) có đặc tính mở kênh , được nghiên cứu sau. Các kết quả này chứng minh rằng quá trình khử hoạt được điều khiển bởi 19 acid amin trong vùng amino-cuối cùng trong vùng tế bào chất của kênh và tạo nên quả cầu và chuỗi amino acid (Hoshi, Zagotta,và Aldrich, 1990). Được kết hợp với quá trình hoạt hóa kênh chính là sự chuyển động của các điện tích âm bên trong một vùng tế bào chất của kênh, vùng này sau đó hút các quả cầu tích điện dương , chuyển động của quả cầu dẫn tới quá trình đóng kênh ( quả cầu này vượt quá kích thước miệng kênh).
Một vài giả thuyết được kiểm nghiệm bằng xác định vùng đột biến, theo đó đoạn protein đặc biệt bị bỏ đi hoặc thêm vào giống như minh họa hoặc các thao tác tương tự được thực hiện ( Krueger, 1989 ). Bằng việc kiểm tra các đặc tính thay đổi của kênh đã được giải thích trong Noãn bào Xenopus, người ta có thể dự đoán chức năng của một đoạn protein nào đó. Tất nhiên, vì sự thay đổi có thể ảnh hưởng tới cấu trúc bậc có nhưng ảnh hưởng phức tạp tới cấu trúc bậc ba ( chưa rõ), vì vậy kết quả cuối cùng mới chỉ được coi là kết quả thử nghiệm.
Cấu trúc kênh : Các phương pháp tạo ảnh
Phương pháp tạo ảnh trực tiếp của các protein màng tế bào thực sự cung cấp những thông tin về cấu trúc như mong muốn. Tinh thể học tia X ( X ray crystallography ) được sử dụng để nghiên cứu các đại phân tử từ mức độ nguyên tử, nhưng nó chỉ được dùng khi các phân tử lặp lại đều đặn. Nó thông thường không có khả năng kết tinh các phân tử protein màng tế bào, các mảng 2 chiều của các protein lọc tập trung được hợp thành vào lớp lipid kép với khoảng không gian đều đặn hợp lý. Sự nhiễu xạ tia X và kính hiển vi điện tử ( EM ) được sử dụng để phân tích và tạo nên các hình ảnh với độ phân giải vừa phải. Một ví dụ đơn giản là kiểm tra qua kính hiển vi về receptor nhận biết acetylcholine chức năng cơ thần kinh Torpedo ( nAChR) ( Toyoshima và Unwin, 1988). Phân tử được tìm thấy có đường kính 8 nm, với giếng ở tâm là 2.0 nm. Quan sát trên bề mặt, protein có hình giống hình hoa thị với 5 nhánh con. Chức năng các nhánh nhỏ là chọc thủng kênh có nước. Nhưng độ phân giải của hình ảnh là quá lớn để xác định lỗ ở tâm và hình dạng cụ thể.
Người ta cho rằng lỗ ở tâm ( central pore ) không có đường kính xác định và được miêu tả trên hình 4.29 có một phần nhỏ hoạt động giống như một bộ lọc có chọn lọc. Vì các các nhánh con trong môi trường nội bào xuất hiện được định hướng là hướng tán nổi với lỗ tạo nên một khoảng không gian với hình thù xác định, chính không gian này rất nhạy cảm với góc nghiêng của các nhánh con. Sự thay đổi góc nghiêng phát sinh do sự thay đổi của điện thế trong màng tế bào ( ví dụ như sự thay đổi lực tĩnh điện ) có thể làm nhanh chóng chuyển kênh từ trạng thái mở sang đóng . Giả thuyết này được đưa ra bởi (Zampighi and Simon, 1985).
Độ dẫn ion phụ thuộc vào độ dẫn của đơn kênh
Mạch điện tương đương của 1 kênh đơn lẻ là 1 loạt các điện trở với nguồn điện và các khóa đóng mở. ( Tất nhiên có 1 điện dung mắc song song, minh họa cho chất điện môi của lớp lipid kép ). Nguồn điện tượng trưng cho điện thế Nernst của ion mà được thấm qua trong khi đó thì khóa đóng mở thể hiện các trạng thái có thể, và đã được đề cập ở trên ( mở, đóng và khử hoạt tính ). Trên hình 4.29, đường kính của lỗ thấm nước là 2,5 nm và chiều dài là 12,0 nm, với điện trở suất khối với 250 cm là 105 pS – đây là giá trị nằm trong khoảng giá trị đã được xác định bằng thực nghiệm. ( Vì kênh có kích thước nguyên tử nên mô hình được sử dụng ở đây là cực kỳ đơn giản và các kết quả số học cần phải xem như là các giá trị ngẫu nhiên. Các thông tin chi tiết hơn về các yếu tố có thể tìm thấy trong cuốn Hille 1992. Dựa vào mô hình này xác định được dòng qua kênh là iK = γK(Vm - VK), trong đó γK là độ dẫn của kênh, VK là điện thế Nerst ( ở đây là cho Kali). Dưới những điều kiện bình thường, độ dẫn của kênh được xem như một hằng số vì vậy sự thay đổi vĩ mô của độ dẫn ion phát sinh từ sự thay đổi trong thành phần của kênh mở ( chính xác là sự ảnh hưởng của các biến mở cổng kênh n, m và h đối với độ dẫn ion trong trục thần kinh của mực ống ).
Hoạt động về mặt thống kê của một kênh đơn lẻ có thể đạt được bằng cách kiểm tra hoạt động của một số lượng lớn các kênh xác định và độc lập và các nhánh con của chúng ( một nhánh con đơn lẻ là một bộ phận đơn giản nhất của một tổng thể ). Nếu Nc là số nhánh con khi đóng trong tổng thể và No là số nhánh con khi mở, khi đó coi các quá trình tỉ lệ bậc nhất với α là hệ số tốc độ truyền từ trạng thái đóng sang mở và β là tốc độ cho quá trình chuyển trạng thái từ mở sang đóng cho biểu thức :
(4.34)
Từ đó thu được biểu thức vi phân :
( 4.35)
Vì
tổng
số
các
nhánh
con
là
N
phải
thỏa
mãn
điều
kiện
N
=
Nc(t)
+
No(t)
với
N
là
1
số
xác
định,
thì
biểu
thức
trên
trở
thành :
( 4.36)
Chia biểu thức 4.36 cho N và thay n = No/N là xác suất thống kê mà bất cứ nhánh con đơn lẻ nào cũng mở, chúng ta có :
(4.37)
phù hợp với biểu thức 4.12. Kết quả này dẫn đến sự miêu tả của Hodgkin- Huxley của các màng tế bào vĩ mô bằng hoạt động của một kênh thành phần đơn lẻ. Đặc biệt hệ số tốc độ truyền α và β cho thấy tốc độ chuyển trạng thái đóng sang mở và mở sang đóng. Vì vậy có thể tính sự chuyển động của các phần tử n - đã được Hodgkin Huxley giới thiệu, như là một cách miêu tả khác theo vật lý đối với tốc độ đã nói ở trên ( chú ý rằng n là một biến liên tục và vì vậy “ giá trị ngưỡng “ là không được xem xét trong một kênh đơn lẻ ). Giá trị ngưỡng là một đặc tính của các màng tế bào vĩ mô với chẳng hạn các kênh kali, natri và các kênh dò và giá trị ngưỡng miêu tả các điều kiện mà hoạt động chung của tất cả các loại kênh cho phép để tạo nên sườn dương của xung hoạt động. Với xác suất kênh Kali ở trên khi ở trạng thái mở là n^4.
Trong khi những miêu tả ở trên xoay quanh hoạt động đồng thời của một số lượng lớn các kênh tương đương , nó cũng đã miêu tả các con số liên quan tới hoạt động liên tiếp của một kênh đơn lẻ ( tức là tính ergodic ) . Nếu bước điện áp màng tế bào được đặt vào tổng thể của các kênh đã nói ở trên, thì nghiệm của phương trình 4.36 là:
(4.38)
Nó miêu tả sự thay đổi theo hàm mũ số lượng nhánh con mở và cũng cho thấy xác suất n đối với một kênh đơn cũng tăng hàm mũ. Nhưng nếu không có điện thế đặt vào , thì có thể quan sát quá trình đóng mở kênh đơn lẻ ngẫu nhiên. Tuy nhiên, dựa vào thuyết biến thiên – suy giảm ( fluctuation – dissipation ) ( Kubo, 1966 ), cùng một hằng số thời gian tác động lên sự biến thiên này cũng giống như tác động tới các thay đổi vĩ mô được mô tả như trong biểu thức 4.38. Nhiều công trình đã phải dựa trực tiếp vào việc nghiên cứu nhiễu ở màng tế bào ( membrane noise ) bằng thực nghiệm (DeFelice, 1981).. về các số kênh đơn. (DeFelice, 1981)..
REFERENCES
Armstrong CW, Hille B (1972): The inner quaternary ammonium ion receptor in potassium channels of the node of Ranvier. J. Gen. Physiol. 59: 388-400.
Baker PF, Hodgkin AL, Shaw TI (1962): The effects of changes in internal ionic concentrations on the electrical properties of perfused giant axons. J. Physiol. (Lond.) 164: 355-74.
Bezanilla F (1986): Voltage dependent gating. In Ionic Channels in Cells and Model Systems, ed. R Latorre, pp. 37-52, Plenum Press, New York.
Cole KS (1949): Dynamic electrical characteristics of squid axon membrane. Arch. Sci. Physiol. 3: 253-8.
Cole KS, Curtis HJ (1939): Electrical impedance of the squid giant axon during activity. J. Gen. Physiol. 22: 649-70.
Cole KS, Moore JW (1960): Potassium ion current in the squid giant axon: Dynamic characteristics. Biophys. J. 1: 1-14.
DeFelice LJ (1981): Introduction to Membrane Noise, 500 pp. Plenum Press, New York.
Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ (1981): Improved patch clamp techniques for high resolution current recording from cells and cell-free membranes. Pflüger Arch. ges. Physiol. 391: 85-100.
Hille B (1970): Ionic channels in nerve membranes. Prog. Biophys. Mol. Biol. 21: 1-32.
Hille B (1992): Ionic Channels of Excitable Membranes, 2nd ed., 607 pp. Sinauer Assoc., Sunderland, Mass. (1st ed., 1984).
Hodgkin AL (1954): A note on conduction velocity. J. Physiol. (Lond.) 125: 221-4.
Hodgkin AL, Horowicz P (1959): The influence of potassium and chloride ions on the membrane potential of single muscle fibers. J. Physiol. (Lond.) 148: 127-60
Hodgkin AL, Huxley AF (1952a): The components of membrane conductance in the giant axon of Loligo. J. Physiol. (Lond.) 116: 473-96.
Hodgkin AL, Huxley AF (1952b): Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. (Lond.) 116: 449-72.
Hodgkin AL, Huxley AF (1952c): The dual effect of membrane potential on sodium conductance in the giant axon of Loligo. J. Physiol. (Lond.) 116: 497-506.
Hodgkin AL, Huxley AF (1952d): A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 117: 500-44.
Hodgkin AL, Huxley AF, Katz B (1952): Measurement of current-voltage relations in the membrane of the giant axon of Loligo. J. Physiol. (Lond.) 116: 424-48.
Hoshi T, Zagotta WN, Aldrich RW (1990): Biophysical and molecular mechanisms of shaker potassium channel inactivation. Science 250: 533-68.
Huxley A (1993): Personal communication.
Jack JJB, Noble D, Tsien RW (1975): Electric Current Flow in Excitable Cells, 502 pp. Clarendon Press, Oxford.
Junge D (1992): Nerve and Muscle Excitation, 3rd ed., 263 pp. Sinauer Assoc., Sunderland, Mass.
Krueger BK (1989): Toward an understanding of structure and function of ion channels. FASEB J. 3: 1906-14. Kubo R (1966): The fluctuation-dissipation theorem. Rep. Prog. Phys. Lond. 29: 255.
Llano I, Webb CK, Bezanilla F (1988): Potassium conductance of the squid giant axon. J. Gen. Physiol. 92:179-196.
Marmont G (1949): Studies on the axon membrane. I. A new method. J. Cell. Comp. Physiol. 34: 351-82.
Moore JW, Blaustein MP, Anderson NC, Narahashi T (1967): Basis of tetrodotoxin's selectivity in blockage of squid axons. J. Gen. Physiol. 50: 1401-11.
Narahashi T, Moore JW, Scott WR (1964): Tetrodotoxin blockage of sodium conductance increase in lobster giant axons. J. Gen. Physiol. 47: 965-74.
Neher E, Marty A (1982): Discrete changes of cell membrane capacitance observed under conditions of enhanced secretion in bovine adrenal chromaffin cells. Proc. Nat. Acad. Sci. USA 79: 6712-6.
Neher E, Sakmann B (1976): Single-channel currents recorded from membrane of denervated frog muscle fibers. Nature 260: 799-802.
Neher E, Sakmann B (1992): The patch clamp technique. Sci. Am. 266:(3) 28-35.
Noble D (1966): Application of Hodgkin-Huxley equations to excitable tissues. Physiol. Rev. 46:(1) 1-50.
Patlak JB, Ortiz M (1986): Two modes of gating during late Na+ channel currents in frog sartorius muscle. J. Gen. Physiol. 87: 305-26.
Plonsey R (1969): Bioelectric Phenomena, 380 pp. McGraw-Hill, New York.
Sakmann B, Neher E (1983): Single Channel Recording, 496 pp. Plenum Press, New York.
Sakmann B, Neher E (1984): Patch clamp techniques for studying ionic channels in excitable membranes. Annu. Rev. Physiol. 46: 455-72.
Toyoshima C, Unwin N (1988): Ion channel of acetylcholine receptor reconstructed from images of postsynaptic membranes. Nature 336: 247-50.
Unwin PNT, Zampighi G (1980): Structure of the junctions between communicating cells. Nature 283: 545-9.
Young JZ (1936): The giant nerve fibers and epistellar body of cephalopods. Q. J. Microsc. Sci. 78: 367-86.
Zambighi GA, Simon SA (1985): The structure of gap junctions as revealed by electron microscopy. In Gap Junctions, ed. MVL Bennett, DC Spray, pp. 13-22, Cold Spring Harbor Laboratory, Cold Spring Harbor, N.Y.
| trang trước | Phản ứng tích cực của màng tế bào | Trang tiếp |