Sách:Điện từ sinh học/Hiện tượng màng tế bào
Giới thiệu chung
Trong chương trước, chúng ta đã thảo luân một cách định tính về diễn biến dưới ngưỡng của tế bào thần kinh. Chương này sẽ miêu tả về chức năng sinh lý cơ bản của hiệu điện thế nghỉ và đáp ứng ngưỡng con của axon để kích thích điện từ từ bối cảnh về lượng. Màng đóng vai trò rất quan trọng trong vệc thiết lập thuộc tính nghỉ và hoạt động điện của tế bào kích thích, qua đó điều chỉnh sự di chuyển của các ion giữa không gian ngoại bào và nội bào. Từ ion ( Tiếng Hy Lạp là “that which goes”) được giới thiệu bởi Faraday vàn năm 1834. Thật dễ dàng để một ion đi qua màng tế bào, hiện tượng này được gọi là độ thấm màng, nó khác với các loại ion khác; sự thấm có chọn lọc này là một kết quả rất quan trọng. sự hoạt động của tế bào sẽ ảnh hưởng tới trạng thái của nó bởi sự thay đổi độ thấm từ. Một điều quan trọng nữa với sự di chuyển của on qua màng là trên thực tế thì các thành phần cấu tạo của các ion bên trong màng tế bào khác rất nhiều vói các ion ở bên ngoài màng. Do đó, nồng độ gradient tồn tại trong tất cả các ion xuyên mà chúng tham gia vào sự di chuyển của các lưới hay dòng ion. Phương pháp mà nhờ đó các dòng ion từ nơi có nồng độ cao xuống nơi có nồng độ thấp được gọi là sự khuyếch tán.
Một kết quả nữa của dòng ion này là xu hướng các ion tập trung ở bên trong và bên ngoài bề mặt màng tế bào, một quá trình mà các trường electron được thành lập bên trong màng. Trường này tác dụng lực lên các ion qua màng tế bào ngay khi được nạp điện. Do đó, sự mô tả sự di chuyển của các ion màng tế bào, các lực điện trường cũng như lực khuyếch tán cần phải được chú trọng. Trạng thái cân bằng có được khi lực khuyếch tán cân bằng với lực điện trường của tất cả các ion xuyên.
Đối với màng tế bào, nó cũng chỉ cho thấm qua một loại ion, điều kiện cân bằng là lực do điện trường tạo ra cân bằng và ngược dấu với lực khuyếch tán. Trong phần tiếp theo, chúng ta sẽ nghiên cứu ‘Cân bằng Nernst’, nó thể hiện sự liên kết của điện thế cân bằng với nồng độ tỉ đối nhất định. Cân bằng cũng có thể được xác định bằng hiệu điện thế điện hóa trên cả hai bề mặt của màng tế bào.
Cân bằng Nernst có được từ hai khái niêm cơ bản bao gồm khái niêm về sự tạo thành dòng ion từ lực điện trường và lực khuyếch tán đó. Do đó, Sự nghiên cứu chặt chẽ về nhiệt động lực học sẽ có giá trị áp dụng và những độc giả quan tâm nên tham khảo những chỉ dẫn của van Rysselberghe (1963) and Katchalsky and Curran (1965) trong cuốn sách.,
Chúng ta cũng sẽ được tìm hiểu về cân bằng Goldman-Hodgkin-Katz, nó sẽ cho chúng ta giá trị trạng thái ổn định của điện thế màng khi có một vài dạng ion trong môi trường nội bào và ngoại bào và khi chung xuyên qua màng tế bào. Chúng ta sẽ biết được, cân bằng Goldman-Hodgkin-Katz là một phần mở rộng đơn giản của cân bằng Nernst.
Một thực thể hóa học nữa được thảo luận chi tiết, cái mà đóng góp phần lớn vào chương này, có thể được tìm thấy trong các sách giáo khoa như là Edsall and Wyman (1958) and Moore (1972).
3.2 Cân bằng NERNST
3.2.1 Điện thế và điện trường
Trong tĩnh điện học, điện thế Φ tại điểm P được xác định bằng công cần thiết để di chuyển một một điện tích dương từ một vị trí tham chiếu I tới P. Nếu điện thế tại điểm tham chiếu là ΦO và điện thế và tại P được kí hiệu là ΦP, khi đó, công We là công cần thiết để di chuyển một đại lượng điện tích Q từ O tới P
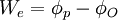 (3.1)
(3.1) |
trong đó
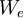 =
Công
[J/mol]
=
Công
[J/mol]
Q = Điện tích [C] (Cu long)
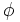 =
Hiệu
điện
thế
[V]
=
Hiệu
điện
thế
[V]
Trong
vấn
đề
điện
sinh
lý
học,
số
lượng
ion
thường
được
tính
bằng
mol.
(
Một
mol
thì
bằng
khối
lượng
phân
tử
trong
6.0225×
10^23,
đó
là
số
Avogadro
phân
tử).
Nếu
một
mol
của
ion
truyền
qua
màng
tế
bào
từ
điểm
tham
chiếu
0
có
điện
thế
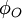 tới
điểm
P
có
điên
thế
tới
điểm
P
có
điên
thế
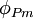 ,
ta
có
bảng
phương
trình:
,
ta
có
bảng
phương
trình:
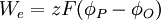 |
trong đó
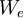 =
Công
[J/mol]
=
Công
[J/mol]
z = Hóa trị nguyên tố
F = hằng số Faraday [9.649 x 10^4 (C/mol)]
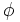 =
Hiệu
điện
thế
[V]
=
Hiệu
điện
thế
[V]
Hằng
số
Faraday
làm
chuyển
đổi
một
lượng
mol
với
điện
lượng
cho
một
đơn
vị
ion.
Hệ
số
z,
được
gọi
là
hóa
trị,
được
đưa
vào
một
ion
đa
trị
và
cũng
được
đưa
dấu
vào.
Chú
ý
rằng
nếu
cả
2
số
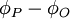 và
z
đều
có
trị
dương
(
ví
dụ:
trường
hợp
mà
điện
tích
dương
được
di
chuyển
qua
từ
nơi
có
điện
thế
thấp
đến
điện
thế
cao),
khi
đó,
cần
công
thực
hiện
và
công
và
z
đều
có
trị
dương
(
ví
dụ:
trường
hợp
mà
điện
tích
dương
được
di
chuyển
qua
từ
nơi
có
điện
thế
thấp
đến
điện
thế
cao),
khi
đó,
cần
công
thực
hiện
và
công
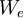 này
dương
như
mong
đợi.
này
dương
như
mong
đợi.
Điện
trường
được
xác
định
bằng
lực
tác
dụng
lên
một
đơn
vị
điện
tích.
Nếu
một
đơn
vị
điện
tích
dương
đi
từ
điểm
tham
chiếu
O
tới
điểm
P,
độ
dịch
chuyển
các
véc
tơ
đồng
vị
là
d
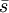 ,
khi
đó
công
chống
lại
lực
điện
trường
là
,
khi
đó
công
chống
lại
lực
điện
trường
là
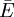 ,
theo
định
luật
bảo
toàn
cơ
học
thì
công
dW
đựoc
tính
bởi
,
theo
định
luật
bảo
toàn
cơ
học
thì
công
dW
đựoc
tính
bởi
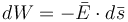 (3.3)
(3.3) |
Từ 3.1 và 3.3 thay thế Q ta được
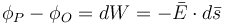 |
Áp dụng khai triển Taylor của trường đại lượng vô hướng với điểm O và s bước ta được
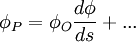 (3.6)
(3.6) |
Khi P rất gần tới O, số hạng cao hơn còn lại sẽ được là một chuỗi khai triển như ở 3.5. Số hạng thứ 2 ở bên phải của biểu thức 3.5 được tính theo đạo hàm của Φ theo hướng s. Sau đó, bằng phép giải tích vecto theo gradient, cho ta . Do đó, 3.5 tương đương với
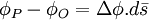
Từ
3.4
và
3.6
suy
ra:
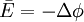 (3.7)
(3.7)
Theo định luật Ohm, quan hệ giữa mật độ dòng điện và cường độ điện trường được cho bởi công thức
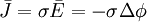 (3.8)
(3.8)
Trong đó, σ là độ dẫn của môi trường, đó là lí do mà dòng này được gọi là dòng điện dẫn.
Vấn đề chính mà chúng ta quan tâm trong các hạt điện tích là bắt nguồn từ sự ion hóa trong chất điện phân và đặc biệt là các ion hiện tại trong và ngoài không gian màng của các tế bào kích thích điện. Bởi do điện tích của chúng, nên ngay lập tức, một số ion bị chịu tác dụng của lực điện trường ở trên. Dòng chảy ion này ( ví dụ dòng trên một đơn vị diện tích trên một đơn vi thời gian) có được từ sự có mặt của điện trường, nó phụ thuộc vào điện trở, theo đó, nó còn là đặc trưng của độ linh động của các loại ion. Sau đó nó đựoc xác định bởi UK là vận tốc mà nó có thể đạt được bởi kth ion trong một đơn vị điện trường. Khi đó dòng ion được xác định bởi
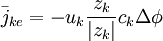
trong đó
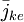 =
dòng
ion
[mol/s.cm^2]
=
dòng
ion
[mol/s.cm^2]
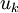 =
độ
linh
động
của
ion
[cm^2/(V.s)]
=
độ
linh
động
của
ion
[cm^2/(V.s)]
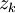 =
hóa
trị
của
ion
=
hóa
trị
của
ion
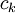 =
nồng
độ
ion
[mol/cm^3]
=
nồng
độ
ion
[mol/cm^3]
và
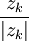 =
kí
hiệu
chiều
của
lực
(dương
đối
với
cation
và
âm
đối
với
anion)
=
kí
hiệu
chiều
của
lực
(dương
đối
với
cation
và
âm
đối
với
anion)
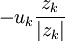 =
vận
tốc
trung
bình
đạt
được
bởi
các
ion
trong
điện
trường
=
vận
tốc
trung
bình
đạt
được
bởi
các
ion
trong
điện
trường
k ở đây chỉ ra đó la đối với k^th ion
Sự
tăng
của
nồng
độ
ion
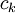 do
vận
tốc
của
dòng
ion.
So
sánh
giữa
3.8
và
3.9
ta
thấy
rằng
độ
linh
động
tỉ
lệ
với
độ
dẫn
của
k^th
ion
trong
chất
điện
phân.
Nồng
độ
ion
phụ
thuộc
vào
độ
nhớt
của
dung
môi
và
kích
thước
với
điện
tích
của
ion
do
vận
tốc
của
dòng
ion.
So
sánh
giữa
3.8
và
3.9
ta
thấy
rằng
độ
linh
động
tỉ
lệ
với
độ
dẫn
của
k^th
ion
trong
chất
điện
phân.
Nồng
độ
ion
phụ
thuộc
vào
độ
nhớt
của
dung
môi
và
kích
thước
với
điện
tích
của
ion
3.2.2 Khuyếch tán
Nếu nồng độ ion đặc trưng không đồng nhất trong bộ phận, sẽ xuất hiện sự phân phối lại, kết quả cuối cùng là làm cho nồng độ phân bố đều. Để thực hiện điều này thì dòng phải chiếm không gian từ vùng có mật đô cao đến thấp. Quá trình này được gọi là khuyếch tán, và sự mô tả định lượng về nó được thể hiện bằng định luật Fick (Fick, 1985)
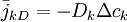 (3.10)
(3.10)
trong đó
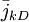 =
dòng
ion
(có
được
do
khuyếch
tán)
[mol/(s.cm^2)]
=
dòng
ion
(có
được
do
khuyếch
tán)
[mol/(s.cm^2)]
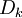 -
hằng
số
Fick
(hằng
số
khuyếch
tán)[cm^2/s]
-
hằng
số
Fick
(hằng
số
khuyếch
tán)[cm^2/s]
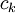 =
nồng
độ
ion
[mol/cm^3]
=
nồng
độ
ion
[mol/cm^3]
Công thức này miêu tả rằng dòng chảy về hướng có nồng độ giảm ( dấu trừ thể hiện điều này), như mong đợi Hằng số Fick có liên hệ với lực khuyếch tán (ví dụ - ck ) để tạo thành dòng của chất k^th. Theo cách tương tự như vậy, độ linh động kết hợp lực điện trường (- Φ) để tạo thành dòng ion. Từ trong trường hợp này, các dòng bị giới hạn bởi các nhân tố giống nhau ( xung đột với các phân tử hòa tan), một liên kết giữa uk và Dk cùng phải tồn tại. Mối quan hệ này được tình bày bởi by Nernst (1889) và Einstein (1905), đó là:
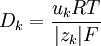 (3.11)
(3.11)
trong đó
T = nhiệt độ tuyết đối [K]
R = hằng số khí [8.314J/(mol.K)]
3.2.3 Phương trình Nernst-Planck
Dòng ion với k^th ion là k, được cho bởi tổng của các dòng ion có được do khuyếch tán và điện trường từ phương trình 3.10 và 3.9/ Dùng mối quan hệ Einstein của phương trình 3.11, nó có thể thể hiện bằng:
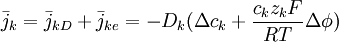 (3.12)
(3.12)
Phương trình 3.12 còn được gọi là phương trình Nernst-Planck (sau Nernst, 1888, 1889; Planck, 1891ab). Nó thể hiện dòng của ion k^th dưới ảnh hưởng của cả gradient nồng độ và điện trường. Một đoạn của nó phụ thuộc vào việc dùng để thể hiện nồng độ ion và vận tốc. Thông thường, đơn vị của nó là [mol/(cm²•s)].
Dòng
ion
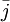 có
thể
biến
đổi
trong
mật
độ
dòng
điện
có
thể
biến
đổi
trong
mật
độ
dòng
điện
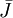 nhân
với
độ
cảm
zF,
số
điện
tích
được
trong
các
phân
tử
(
là
Culong,
C).
Kết
quả
là,
đối
với
ion
k^th
nhân
với
độ
cảm
zF,
số
điện
tích
được
trong
các
phân
tử
(
là
Culong,
C).
Kết
quả
là,
đối
với
ion
k^th
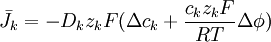 (3.13)
(3.13)
trong đó
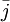 =
mật
độ
dòng
điên
của
k^th
ion
C/(s•cm^2)]
=
[A/cm^2]
=
mật
độ
dòng
điên
của
k^th
ion
C/(s•cm^2)]
=
[A/cm^2]
Từ phương trình 3.11 và 3.13 ta có thể viết lại
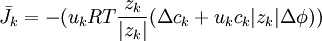
3.2.4 Điện thế Nernst
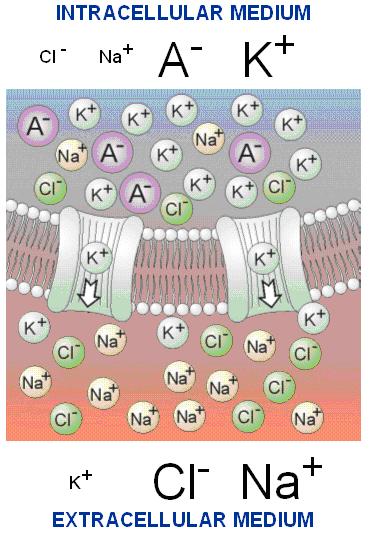
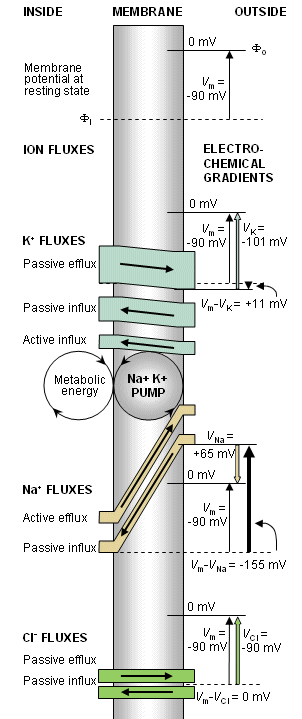
Hình 3.1 miêu tả một phần nhỏ của màng tế bào của tế bào kích thích ( ví dụ, tế bào thần kinh và tế bào cơ). Sự thể hiện yếu tố màng tế bào được miêu tả như một patch. Các ion quan trọng là Kali (K+), Natri (Na+), and Clo (Cl-), nhưng chúng ta sẽ giả sử rằng màng chỉ cho thấm qua một ion trong chúng ( Ka), chúng ta kí hiệu đó là ion k^th và công nhận nó là dạng tổng quát sau này. Nồng độ ion trên mỗi bề mặt của màng tế bào cũng không được minh họa dưới dạng biểu đồ hình 3.1. Trong hình, kích thước của các kí tự được tỉ lệ với nồng độ ion tương ứng. Các ion được thể hiện di qua màng thông qua các kênh như chú ý ở trên. Số ion ở dưới qua một kênh mở có thể lên đến hơn 106 trên một giây.
Hình
3.1
Một
phần
màng
của
tế
bào
kích
thích
ở
dạng
nghỉ
với
một
phần
vùng
phụ
cận
bao
quanh
môi
trường
trong
và
ngoài
màng
tế
bào.
Các
ion
chính
có
thể
chảy
qua
màng
là
Kali
(K+),
Natri
(Na+),
and
Clo
(Cl-).
Thành
phần
của
các
ion
trong
và
ngoài
màng
là
không
bằng
nhau.
Trong
hình
vẽ,
kích
thước
của
các
biểu
tượng
ánh
xạ
tỉ
lệ
với
mật
độ
ion
tương
ứng.
Anio
trong
nội
bào
(A-)
rất
quan
trọng
để
hình
thành
điện
tử
trung
tính.
Tuy
nhiên,
A-
được
dẫn
xuất
từ
những
phân
tử
đứng
yên
và
không
thấm
(KA)
do
đó,
A-
không
góp
phần
vào
dòng
ion.
Ở
trạng
thái
nghỉ,
màng
chỉ
cho
thấm
qua
ion
K.
Tỉ
lệ
mật
độ
ion
của
nội
bào
và
ngoại
bào
là
30-50:1
Điều
đó
cho
ta
biết
rằng
đây
là
xấp
xỉ
hợp
lý
trong
điều
kiện
thường
ở
trạng
thái
nghỉ.
Mật
độ
ion
K
trong
nội
bào
thông
thường
gấp
khoảng
30
–
50
lần
ở
ngoại
bào.
Kết
quả
là
ion
K
sẽ
khuyếch
tán
ra
ngoài
màng
tế
bào,
mất
đi
một
khoảng
bằng
số
ion
âm
(
Clo
là
chủ
yếu).
Bởi
vì
lực
hút
tĩnh
điện
lớn,
như
là
sự
xuất
hiện
của
dòng
K,,
ion
K
sẽ
tích
trữ
ở
ngoài
màng
tế
bào.
Đồng
thới
một
số
ion
CL
(
ở
bên
dưới
phía
trái
từ
nguyên
tử
KCl
cũng
tích
trữ
ở
phía
ngoài
màng.
Thực
tế,
điện
dung
của
màng
là
có
trong
qua
trình
nạp
điện
và
điện
trường
xuất
hiện
có
hướng
vào
trong
tỉ
lệ
với
dòng
k
thực.
Sự
mô
tả
cao
hơn
của
quá
trình
này
sẽ
không
tiếp
tục
một
cách
mơ
hồ
bởi
vì
điện
trường
tăng
sẽ
làm
cho
các
ion
Kali
thấm
qua
được
hướng
trực
tiếp
vào
phía
trong,
do
đó,
nó
ngược
với
lực
khuyếch
tán.
Trạng
thái
cân
bằng
sẽ
đạt
được
khi
hai
lực
có
độ
lớn
bằng
nhau.
Số
ion
Kali
yêu
cầu
qua
màng
tế
bào
thường
cực
kì
nhỏ
và
có
thể
đếm
được.
Vì
vậy,
quá
trình
trên
có
một
ý
nghĩa
thiết
thực,
chúng
ta
sẽ
quan
tâm
tới
mật
độ
của
ion
Kali
trong
và
ngoài
màng
tế
bào
khi
điện
áp
qua
không
đổi.
Điện
thế
qua
mâng
đạt
được
ở
trạng
thái
cân
bằng
được
gọi
đơn
giản
là
điện
thế
cân
bằng.
Mối
quan
hệ
về
lượng
giữa
mật
độ
ion
K
và
điện
thế
cân
bằng
đã
được
đề
cập
đến
ở
trên
có
thể
nhận
được
từ
phương
trình
Nernst-Planck.
Để
có
kết
quản
tổng
quát,
chúng
takí
hiệu
ion
K
là
kth
ion.
Áp
dụng
phương
trình
3.13
với
màng
ở
trạng
thái
cân
bằng,
chúng
ta
sẽ
đáp
ứng
được
điều
kiện
dòng
zero
để
có.
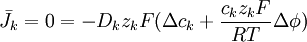 (3.15)
(3.15)
Trong đó, k kí hiệu cho kth ion, mặt khác, từ 3.15 ta còn có
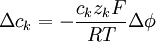 (3.16)
(3.16)
Khi màng cự kì mỏng, chúng ta có thể xét đến bất kì miếng vá nhỏ nào như là hai chiều và sự miêu tả thay đổi qua một chiều (từ bình thường đến màng). Nếu chúng ta gọi hướng đó là x, thì 3.16 có thể viết lại thành:
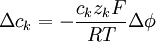 (3.17)
(3.17)
Phương trình 3.17 có thể sắp xếp lại thành
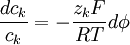 (3.18)
(3.18)
Bây giờ 3.18 sẽ được lấy tích phân một khoảng từ không gian trong nội bào và ngoại bào, đó là:
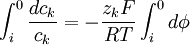 (3.19)
(3.19)
Phép tích phân trong 3.19 sẽ cho chúng ta
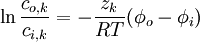 (3.20)
(3.20)
Trong
đó,
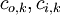 kí
hiệu
lần
lượt
cho
mật
độ
trong
và
ngoài
tế
bào
của
kth
ion.
Theo
quy
ước,
điện
thế
cân
bằng
qua
màng
của
kth
ion
bằng
điện
thế
trong
trừ
đi
điện
thế
ngoài
màng
(Vk
=
Φi
-
Φo),
do
đó:
kí
hiệu
lần
lượt
cho
mật
độ
trong
và
ngoài
tế
bào
của
kth
ion.
Theo
quy
ước,
điện
thế
cân
bằng
qua
màng
của
kth
ion
bằng
điện
thế
trong
trừ
đi
điện
thế
ngoài
màng
(Vk
=
Φi
-
Φo),
do
đó:
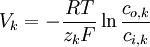 (3.21)
(3.21)
trong đó
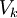 là
điện
thế
cân
bằng
với
k^th
ion
qua
màng
Φi
-
Φo
ví
dụ
điện
thế
Nernst
[V]
là
điện
thế
cân
bằng
với
k^th
ion
qua
màng
Φi
-
Φo
ví
dụ
điện
thế
Nernst
[V]
R = hằng số khí [8.314 J/(mol.K)]
T = Nhiệt độ tuyệt đối
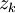 =
hóa
trị
của
k^th
ion
=
hóa
trị
của
k^th
ion
F = hằng số Faraday [9.649 x 104 C/mol]
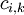 =
nồng
độ
nội
bào
của
k^th
ion
=
nồng
độ
nội
bào
của
k^th
ion
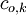 =
nồng
độ
ngoại
bào
của
k^th
ion
=
nồng
độ
ngoại
bào
của
k^th
ion
Phương trình 3.21 là phương trình nổi tiếng Nernst, được tìm thấy bởi Walther Hermann Nernst năm 1888 (Nernst, 1888). Thay thế 37 °C bằng nhiệt độ T = 273+37 và +1 cho hóa trị, đồng thời thay thế logarit tự nhiên ( Loga Nepe) bằng logarit thập phân ( Loga Brigg), có thể viết phương trình Nernst cho một ion dương đơn trị như sau
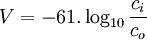 [mV]
(3.22)
[mV]
(3.22)
Ở
nhiệt
độ
phòng
(20
°C),
hệ
số
của
phương
trình
3.22
có
giá
trị
58,
ở
nhiệt
độ
nước
biển
(6
°C),
nó
có
giá
trị
55.
Đây
là
lưu
ý
cuối
cùng
khi
ta
tính
đến
squid
axon.
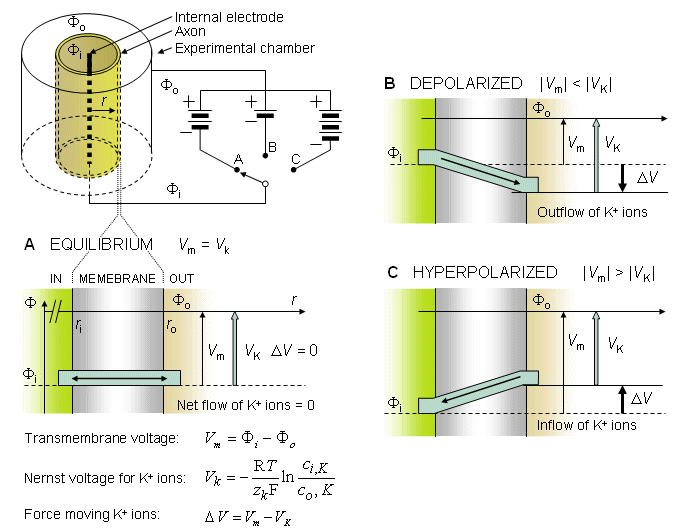
Ví
dụ
Chúng
ta
sẽ
thảo
luận
về
vấn
đề
cân
bằng
một
cách
sâu
hơn
nữa
bằng
cách
lầy
ví
dụ
trong
hình
3.2,
nó
mô
tả
một
sợi
trục
trên
một
khoang
hình
trụ.
Điện
thế
bên
trong
của
sợi
trục
được
nạp
bởi
3
nguồn
pin
có
thể
thay
thế
được
(A,
B,
C),
chúng
có
thể
được
đặt
vào
giữa
không
gian
giữa
nội
bào
và
ngoại
bào.
Chúng
ta
giả
sử
rằng
không
gian
giữa
trong
và
ngoài
màng
tế
bào
có
thể
coi
như
là
đẳng
thế
để
điện
thế
qua
màng
Vm
(khác
với
điện
thế
đi
ngang
qua
màng
)
mọi
nơi
sẽ
như
nhau.
(
Trong
kĩ
thuật
nó
được
gọi
là
voltage
clamp
và
được
giải
thích
chi
tiết
hơn
trong
phần
4.2).
Thêm
vào
đó,
màng
được
giả
sử
là
chỉ
cho
thấm
qua
ion
Kali,
mật
độ
của
ion
Kali
trong
và
ngoài
màng
tế
bào
thứ
tự
là
ci,K
và
co,K
.
Ở
trạng
thái
nghỉ,
điện
thế
màng
Vm
(=
Φi
-
Φo)
bằng
VK,
điện
thế
Nernst
với
ion
K+
được
cho
thưo
phương
trình
3.21.
Trong
hình
3.2,
trục
tung
thể
hiện
điện
thế
Φ,
và
trục
hoành
là
bán
kính
r
từ
trung
giữa
đến
sợi
trục.
Màng
được
xác
định
bằng
bán
kính
ri
và
ro.
Độ
dài
của
mũi
tên
chỉ
ra
độ
lớn
của
điện
thế
(
điện
thế
trong
màng
trừ
đi
điện
thế
ngoài
màng
).
Hướng
của
mũi
tên
chỉ
sự
phân
cực,
trong
đó,
hướng
đi
lên
của
mũi
tên
là
chiều
âm,
đi
xuống
là
chiều
dương
(
bởi
vì
tất
các
điện
thế
khác
nhau
trong
ví
dụ
này
được
đo
từ
điện
thế
âm).
Do
đó,
khi
ΔV
dương
(hướng
xuống),
cường
độ
dòng
điện
màng
(với
ion
dương)
cũng
dương
(
ví
dụ
phía
dưới)
A.
Giả
sử
rằng
sức
điện
động
emf
của
pin
A
bằng
VK.
Khi
Vm
=
VK
và
trong
các
điều
kiện
tương
đối
xác
thực
để
đạt
được
cân
bằng
giữa
lực
khuyến
tán
và
lực
điện
trường.
Dưới
điều
kiện
này,
không
có
lưu
lượng
thực
của
ion
Kali
tồn
tại
qua
màng
tế
bào
(
xem
hình
3.2A
).
Dòng
qua
màng
tế
bào
lúc
này
chỉ
có
dòng
khuyếch
tán
theo
cả
hai
hướng.
B.
Giả
sử
lúc
này
điện
thế
của
pin
B
nhỏ
hơn
VK
(|Vm
<
VK|).
Khi
đó,
điện
thế
bên
trong
màng
trở
nên
ít
âm
hơn,
hiện
tượng
này
gọi
là
sự
khử
cực
của
màng.
Bây
giờ,
điện
trường
không
đủ
lớn
để
cân
bằng
với
lực
khuyếch
tán.
Nó
không
bằng
ΔV
=
Vm
-
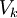 và
kết
quả
là
dòng
ion
kali
chảy
mạnh
ra
(từ
nơi
có
điện
thế
điện
hóa
cao
đến
nơi
có
điện
thế
điện
hóa
thấp).
Hiện
tượng
này
được
minh
họa
trong
hình
3.2B
C.
Mặt
khác,
nếu
pin
C
được
chọn
để
điện
thế
trong
màng
trở
nên
nhiều
âm
hơn
khi
ở
trạng
thái
nghỉ
(|
và
kết
quả
là
dòng
ion
kali
chảy
mạnh
ra
(từ
nơi
có
điện
thế
điện
hóa
cao
đến
nơi
có
điện
thế
điện
hóa
thấp).
Hiện
tượng
này
được
minh
họa
trong
hình
3.2B
C.
Mặt
khác,
nếu
pin
C
được
chọn
để
điện
thế
trong
màng
trở
nên
nhiều
âm
hơn
khi
ở
trạng
thái
nghỉ
(|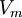 |
>
|
|
>
|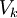 |),
khi
đó
màng
được
gọi
là
siêu
phân
cực
hóa.
Trong
điều
kiện
này,
các
ion
sẽ
chảy
vào
trong
(
ngược
lại
từ
nơi
có
điện
thế
điện
hóa
cao
đến
nơi
có
điện
thế
điện
hóa
thấp).
Hiện
tượng
này
được
minh
họa
trong
hình
3.2C.
|),
khi
đó
màng
được
gọi
là
siêu
phân
cực
hóa.
Trong
điều
kiện
này,
các
ion
sẽ
chảy
vào
trong
(
ngược
lại
từ
nơi
có
điện
thế
điện
hóa
cao
đến
nơi
có
điện
thế
điện
hóa
thấp).
Hiện
tượng
này
được
minh
họa
trong
hình
3.2C.
Hình 3.2 Ví dụ minh họa cân bằng Nernst và dòng ion chày qua màng tế bào trong
(A) cân bằng ở trạng thái nghỉ
(B) khử phân cực màng
(C) siêu phân cực màng
Lực
khuyếch
tán
tăng
lên
lần
lượt
từ
nồng
độ
gradient
đến
cân
bằng
và
ngược
dấu
với
lực
điện
trường
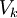 .
Nó
được
tính
bằng
phương
trình
Nernst
(
phương
trình
3.21).
Lực
điện
trường
Nernst
.
Nó
được
tính
bằng
phương
trình
Nernst
(
phương
trình
3.21).
Lực
điện
trường
Nernst
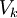 được
minh
họa
bằng
mũi
tên
mở.
Mũi
tên
nhạt
màu
miêu
tả
điện
trường
thực
Vm
qua
màng
tế
bào,
nó
được
áp
đặt
khi
pin
thực
hiện
voltage
clamp
(xem
phần
4.2
để
mô
tả
về
voltage
clamp).
Mũi
tên
đậm
màu
là
lực
phát
động
điện
trường
lưới
ΔV
trong
màng,
kết
quả
có
từ
sự
khác
nhau
giữa
điện
trường
thực
(mũi
tên
nhạt
)
và
điện
trường
cân
bằng
(
mũi
tên
mở
)
được
minh
họa
bằng
mũi
tên
mở.
Mũi
tên
nhạt
màu
miêu
tả
điện
trường
thực
Vm
qua
màng
tế
bào,
nó
được
áp
đặt
khi
pin
thực
hiện
voltage
clamp
(xem
phần
4.2
để
mô
tả
về
voltage
clamp).
Mũi
tên
đậm
màu
là
lực
phát
động
điện
trường
lưới
ΔV
trong
màng,
kết
quả
có
từ
sự
khác
nhau
giữa
điện
trường
thực
(mũi
tên
nhạt
)
và
điện
trường
cân
bằng
(
mũi
tên
mở
)
3.3 Nguồn gốc của điện thế nghỉ
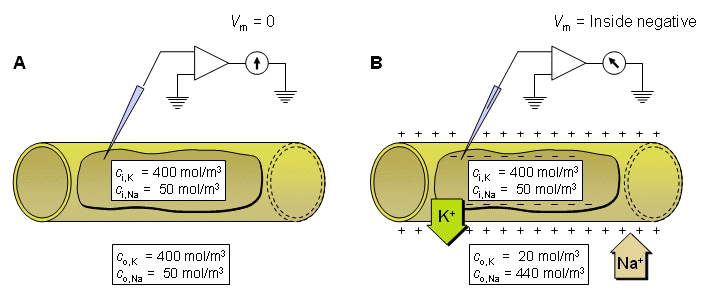
Điện thế nghỉ của tế bào thần kinh thể hiện giá trị của điện thế màng tế bào ( khác với điện thế trong vào ngoài màng tế bào) khi noron thần kinh ở trạng thái nghỉ ở điều kiện tự nhiên trong môi trường sinh lý học. Nó nhấn mạnh rằng điện thế nghỉ không ở tình trạng bị động nhưng rạng thái hoạt động bền cần chuyển hóa năng lượng để duy trì. Julius Bernstein, người sáng lập ra thuyết màng tế bào, đã đề ra một giả thuyết rất cơ bản về nguồn gốc của hiệu điện thế nghỉ, được mô tả ở hình 3.3 (Bernstein, 1902; 1912). Giả thuyết của ông dựa trên các thí nghiệm trên sợi trục của mực ống nơi mà nồng độ ion trong màng đối với Ka là ci,K = 400 mol/m³; và đối với NA là ci,Na = 50 mol/m³. Giả sử rằng màng tế bào chỉ cho thấm qua các ion ion Kali mà không cho thấm qua các ion Na.
Các sợi trục đầu tiên được đặt trong dung dịch mà nồng độ ion của nó giống như bên trong sợi trục. Như trong trường hợp, sự có mặt của màng tế bào không dẫn đến sự biến đổi của hiệu số điện thế giữa trong và ngoài màng tế bào do đó điện thế màng bằng 0.
Sau đó, các sợi trục được đưa vào nước muối, trong đó nồng độ ion kali là co,K = 20 mol/m³ và nồng độ ion Na là co,Na = 440 mol/m³. Lúc này gradient nồng độ tồn tại trong cả hai dạng ion làm cho chúng di chuyển từ nơi có nồng độ cao đến nơi có nồng độ thấp hơn. Tuy nhiên, vì màng tế bào được giả sử là không cho thấm qua ion Na, bất chấp cả gradient nồng độ, chúng không thể di chuyển qua màng tế bào. Mặt khác, ion kali chảy từ trong ra ngoài, khi chúng mang điện tích dương, bên trong sẽ trở nên có tỉ lệ âm hơn so với bên ngoài. Dòng này tiếp tục chảy cho đến khi điện thế màng đạt đến điện thế Nernst với Kali tương ứng, đó là, khi gradient dòng điện và khuyếch tán bằng nhau ( và ngược hướng nhau) và đạt được trạng thái cân bằng. Điện thế tại trạng thái cân bằng được tính từ phương trình Nernst (3.21)
Tuy nhiên, thuyết Bernstein chưa được đầy đủ bởi vì màng không hoàn toàn không cho lọt qua các ion natri. Thay vào đó, đặc biệt là do gradient điện hóa cao, một số ion natri chảy vào trong màng tế bào. Do đó, giống như sự mô tả trước, ion kali chảy ra ngoài màng. Bởi vì điện thế Nernst với ion kali và natri là không bằng nhau nên không có điện thế màng để làm cho hai dòng ion cân bằng.
Vì vậy, điện thế màng tế bào ở trạng thái nghỉ là giá trị với trạng thái ổn định đạt được (ví dụ, nới mà ion natri chảy vào và ion kali chảy ra bằng nhau). Sự chảy vào của dòng ion natri và chảy ra ngoài của dòng ion kali một cách đều đặn cuối cùng sẽ làm thay đổi nồng độ trong màng tế bào ở trạng thái nghỉ và ảnh hưởng đến cân bằng nội; tuy nhiên, bơm Na-K được đề cập đến trước đây sẽ di chuyển ion natri nghược trở lại ngoài màng và ion kali ngược trở lại trong màng, do đó, nó sẽ giữ cho nồng độ ion ổn định. Năng lượng của bơm có được từ chuyển hóa tế bào...
Hình 3.3. Nguồn gốc của điện thế nghỉ theo Julius Bernstein.
3.4 Màng tế bào khi cho thấm qua nhiều loại ion
3.4.1 Cân bằng Donnan
Giả thuyết màng sinh học chỉ cho thấm qua một ion là không hợp lý và độ thấm từ yếu có thể gây nên hiệu ứng qua trọng. Chúng ta sẽ giả sử rằng có nhiều ion được thấm qua, dòng của mỗi ion độc lập với dòng khác ( giả thuyết này được biết đến như là thuyết độc lập và được đua ra bởi Hodgkin and Huxley (1952a)). Giả thuyết này được chứng minh qua nhiều thí nghiệm.
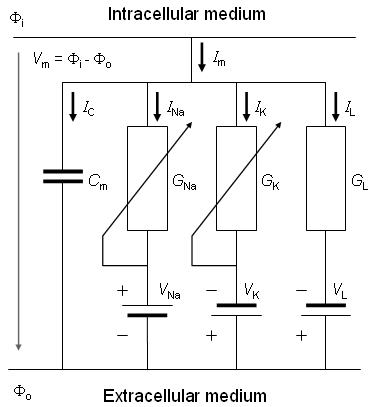
Một
màng
sinh
học
được
biểu
diễn
bởi
kiểu
vẽ
trong
hình
3.4,
nó
có
đưa
vào
nhận
xét
cơ
bản
của
ion
kali,
natri,
và
clo.
Nếu
điện
thế
màng
là
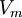 ,
và
khi
,
và
khi
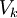 là
điện
thế
cân
bằng
với
k^th
ion,
khi
đó
(
là
điện
thế
cân
bằng
với
k^th
ion,
khi
đó
(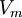 -
-
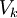 )
là
lực
dẫn
động
lưới
trên
kth
ion.
Ví
dụ
,
nếu
kể
đến
kali
(K),
lực
đẫn
động
là
(
)
là
lực
dẫn
động
lưới
trên
kth
ion.
Ví
dụ
,
nếu
kể
đến
kali
(K),
lực
đẫn
động
là
(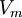 -
-
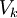 );
ở
đây
chúng
ta
có
thể
nhận
ra
rằng
);
ở
đây
chúng
ta
có
thể
nhận
ra
rằng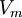 là
lực
điện
trường
và
là
lực
điện
trường
và
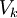 là
lực
khuyếch
tán
(trong
quan
hệ
dòng
điện)
của
kali.
Khi
là
lực
khuyếch
tán
(trong
quan
hệ
dòng
điện)
của
kali.
Khi
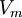 =
=
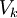 ,lực
dẫn
động
bằng
0
và
không
có
dòng
khi
điện
thế
giống
như
điện
thế
cân
bằng.
Đọ
giả
có
thể
đặt
lại,
,lực
dẫn
động
bằng
0
và
không
có
dòng
khi
điện
thế
giống
như
điện
thế
cân
bằng.
Đọ
giả
có
thể
đặt
lại,
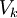 âm;
do
đó
nếu
âm;
do
đó
nếu
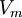 -
-
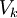 dương
thì
lực
điện
trường
sẽ
nhỏ
hơn
lực
khuyếch
tán
và
kết
quả
là
dòng
kali
chảy
ra
ngoài
(dòng
chuyển
màng
dương)
như
chúng
minh
trong
ví
dụ
ở
phần
3.2.4.
dương
thì
lực
điện
trường
sẽ
nhỏ
hơn
lực
khuyếch
tán
và
kết
quả
là
dòng
kali
chảy
ra
ngoài
(dòng
chuyển
màng
dương)
như
chúng
minh
trong
ví
dụ
ở
phần
3.2.4.
Kết cấu trong và ngoài màng tăng lên từ hoạt động chuyển hóa ( bơm Na-K), chúng sẽ duy trì trì trạng thái không cân bằng này (vấn đề này sẽ được nói sau). Chúng ta có thể thấy, bất chấp dòng ion màng, bơm sẽ luôn luôn hoạt động để trả lại kết cấu ion thông thường. Tuy nhiên, sẽ rất thú vị nếu ta quan tâm tới kết quả cuối cùng nếu bơm không còn được sử dụng (có thể đó là hậu quả của chứng thếu máu cục bộ). Trong trường hợp này, sự chuyển động của các ion rất lớn sẽ xảy ra, đó là kết quả của sự thay đổi kiến trúc ion. Khi đạt được trạng thái cân bằng, mọi ion đều có điện thế Nernst. Tuy nhiên, đó cũng là điện thế chuyển màng thông thường. Sự thật thì do điện thế thông thường này, tỉ lệ nồng độ cân bằng yêu cầu phải thõa mãn phương trình 3.23 (suy ra từ phương trình 3.21)
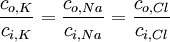 (3.23)
(3.23)
Chú ý rằng, phương trình 3.23 phản ánh sự thật rằng, tất cả các ion đều có hóa trị 1 và clo thì không. Điều kiện được biểu diễn bởi phương trình 3.23 là tất cả các ion đều ở trạng thái cân bằng, đó là cân bằng Donnan
Hình 3.4 Biểu diễn mạch điện của membrane patch
3.4.2 Giá trị của điện thế nghỉ, phương trình Goldman-Hodgkin-Katz
Mối quan hệ giữa điện thế màng và dòng ion là cực kì quan trọng. Để nghiên cứu về mối quan hệ này ta có một số giả thuyết: thứ nhất, đó là màng sinh học là đồng chất và trung lập ( giống như một mảnh kính mỏng); thứ hai, vùng nội bào và ngoại bào hoàn toàn đồng nhất và không đổi. Ví dụ kiểu được miêu tả ở đây là kiểu khuyếch tán điện tử. Các kiểu này được mô tả bởi Goldman-Hodgkin-Katz trong phần này.
Do màng sinh học rất mỏng như đã nói ở bên, chúng ta sẽ xem như bất kì một nguyên tố nào của màng dưới góc độ hai chiều. Giả sử theo kiểu Goldman-Hodgkin-Katz thì màng tế bào là đồng nhất, hai chiều và vô hạn ở bên. Nếu trục x thường được chọn để biểu diễn màng tế bào gốc tại bề mặt của màng trong vùng ngoại bào và độ dày màng là h, thì khi x = h xác định bề mặt của màng trong vùng nội bào. Vì giả sử như đồng nhất như ở bên, sự thay đổi của trường điện thế Φ và nồng độ ion c trong màng chỉ là hàm của x. Giả thiết cơ bản dưới kiểu Goldman-Hodgkin-Katz là trường bên trong màng là hằng số, do đó:
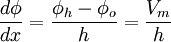 (3.24)
(3.24)
trong đó
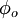 =
điện
thế
tại
bề
mặt
ngoài
của
màng
=
điện
thế
tại
bề
mặt
ngoài
của
màng
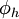 =
điện
thế
tại
ề
mặt
trong
của
màng
=
điện
thế
tại
ề
mặt
trong
của
màng
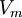 =
điện
thế
chuyển
màng
=
điện
thế
chuyển
màng
h = độ dày màng
Sự xấp xỉ này lần đầu được đưa ra bởi David Goldman (1943) Phương trình Nernst đưa ra giá trị cân bằng của điện thế màng khi màng chỉ cho thấm qua một dạng ion, khi tất cả các ion đều thấm qua được ta có phương trình cân bằng Donnan. Dưới điều kiện sinh lý học, không đạt được trạng thái cân bằng như thí nghiệm trong ví dụ ở bảng 3.1. Để xác định điện thế màng khi có nhiều kiểu ion trong môi trương nội bào và ngoại bào, màng phải có tính thấm và phải dùng một phần mở rộng của phương trình Nernst.
Với
màng
tế
bào
được
đưa
ra
ở
trên,
chúng
ta
có
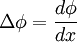 và
và
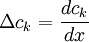 và
dùng
phương
trình
3.12
ta
được
và
dùng
phương
trình
3.12
ta
được
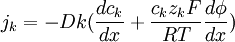 (3.25)
(3.25)
với
dòng
kth
ion.
Nếu
bây
giờ
chúng
ta
chèn
thêm
một
trường
hằng
số
gần
đúng
từ
phương
trình
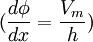 ,
ta
có
,
ta
có
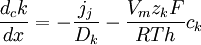 (3.26)
(3.26)
Để lấy vi phân nồng độ ion bên trong màng từ ngoài màng ( ví dụ trong với ngoài màng) chúng ra dùng kí tự c^m ở dưới nơi mà nồng độ trong màng được chỉ ra) . Viết lại phương trình 3.26 cho ta phương trình vi phân dưới đây
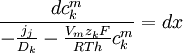 (3.27)
(3.27)
Bây
giờ
chúng
ta
lấy
tích
phân
phương
trình
3.27
trong
màng
từ
cạnh
biên
trái
(x
=
0)
tới
cạnh
biên
phải
(x
=
h).
Giả
sử
rằng
sự
tồn
tại
của
trạng
thái
nghỉ;
do
đó
mỗi
dòng
ion
phải
trong
điều
kiện
ổn
định
và
đồng
nhất
với
x.
Ngoài
ra,
với
Vm
không
đổi
còn
lại,
tổng
cường
độ
dòng
điện
màng
phải
bằng
0.
Từ
điều
kiện
đầu
chúng
ta
cho
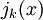 là
hằng
số,
do
đó
trong
mặt
biên
trái
của
phương
trình
3.27,
chỉ
có
là
hằng
số,
do
đó
trong
mặt
biên
trái
của
phương
trình
3.27,
chỉ
có
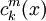 là
hàm
của
x.
Kêt
quả
của
phép
tich
phân
này
là:
là
hàm
của
x.
Kêt
quả
của
phép
tich
phân
này
là:
![{\frac {RTh}{V_{{m}}z_{{k}}F}}\ln[{\frac {{\frac {V_{{m}}z_{{k}}F}{RTh}}c_{{k}}^{{h}}+{\frac {j_{{j}}}{D_{{k}}}}}{{\frac {V_{{m}}z_{{k}}F}{RTh}}c_{{k}}^{{0}}+{\frac {j_{{j}}}{D_{{k}}}}}}]](https://tusach.thuvienkhoahoc.com/images/math/9/8/3/9832ecc0ec7e41e262f026ec54d09733.png) (3.28)
(3.28)
trong
đó,
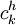 =
nồng
độ
của
=
nồng
độ
của
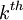 ion
tại
x
=
h
ion
tại
x
=
h
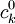 =
nồng
độ
của
=
nồng
độ
của
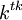 tại
x=0
tại
x=0
Cả hai có thể biến đổi được xác định trong màng.
Từ
phương
trình
3.28
suy
ra
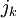 ,
,
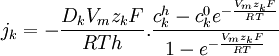 (3.29)
(3.29)
Nồng
độ
của
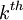 ion
trong
phương
trình
3.29
là
trong
màng
tế
bào.
Tuy
nhiên,
nồng
độ
được
tính
ở
đây
là
ở
trong
không
gian
nội
bào
và
ngoại
bào.
Lúc
này,
tỉ
lệ
mật
độ
ngoài
và
trong
màng
được
mô
tả
bởi
hệ
số
phân
số
,
β,
có
nhiều
giả
định
giống
như
trên
bề
mặt
của
trong
và
ngoài
màng
tế
bào.
Do
đó,
khi
x
=
0
tại
bề
mặt
ngoài
màng
tế
bào
và
x
=
h
tại
bề
mặt
trong
màng,
chúng
ta
có
ion
trong
phương
trình
3.29
là
trong
màng
tế
bào.
Tuy
nhiên,
nồng
độ
được
tính
ở
đây
là
ở
trong
không
gian
nội
bào
và
ngoại
bào.
Lúc
này,
tỉ
lệ
mật
độ
ngoài
và
trong
màng
được
mô
tả
bởi
hệ
số
phân
số
,
β,
có
nhiều
giả
định
giống
như
trên
bề
mặt
của
trong
và
ngoài
màng
tế
bào.
Do
đó,
khi
x
=
0
tại
bề
mặt
ngoài
màng
tế
bào
và
x
=
h
tại
bề
mặt
trong
màng,
chúng
ta
có
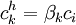 (3.30)
(3.30) |
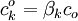 |
trong đó,
β = hệ số phân chia
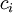 =
Nồng
độ
ion
đo
dược
trong
nội
bào
=
Nồng
độ
ion
đo
dược
trong
nội
bào
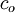 =
Nồng
độ
ion
đo
dược
trong
ngoại
bào
=
Nồng
độ
ion
đo
dược
trong
ngoại
bào
Mật
độ
dòng
điện
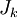 có
thể
tính
được
bằng
cách
nhân
dòng
ion
có
thể
tính
được
bằng
cách
nhân
dòng
ion
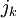 từ
phương
trình
3.29
với
hằng
số
Faraday
và
hóa
trị.
Thêm
vào
đó,
nếu
độ
thấm
từ
phương
trình
3.29
với
hằng
số
Faraday
và
hóa
trị.
Thêm
vào
đó,
nếu
độ
thấm
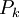 được
xác
định
bằng:
được
xác
định
bằng:
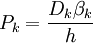 (3.31)
(3.31)
Khi đó
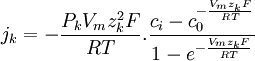 (3.32)
(3.32)
Khi
ta
tính
đến
dòng
ion
qua
màng
tại
trạng
thái
nghỉ,
tổng
của
tất
cả
các
dòng
qua
màng
cần
phải
bằng
0,
như
chú
ý
ở
trên.
Yếu
tố
góp
phần
vào
cường
độ
dòng
điện
là
các
ion
kali,
natri
và
clo.
Vì
vậy
chúng
ta
có
thể
viết
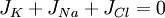 (3.33)
(3.33)
Thay
phương
trình
3.32
vào
3.33,
cộng
thêm
với
the
appropriate
indices,
và
chú
ý
rằng
kali
và
natri
có
hóa
trị
z
=
+1
trong
khi
với
clo
là
z
=
-1
và
bỏ
đi
hằng
số
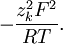 ta
có
ta
có
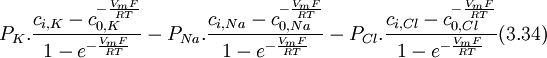
Trong
phương
trình
3.34,
Biểu
thức
cường
độ
dòng
ion
natri
cũng
tương
tự
như
với
kali
(trừ
ra
sự
chuyển
đổi
Na
-
K);
tuy
nhiên,
biểu
thức
yêu
cầu
với
clo
phải
thay
đổi
theo
hàm
mũ,
phản
ánh
hóa
trị
âm.
Mẫu
số
có
thể
được
bỏ
đi
từ
phương
trình
3.34
bằng
cách
nhân
cả
tử
số
và
mẫu
số
với
hệ
số
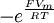 và
sau
đó
nhân
với
1
-
-e^\frac{FV_{m}}{RT}
Do
đó
chúng
ta
có
và
sau
đó
nhân
với
1
-
-e^\frac{FV_{m}}{RT}
Do
đó
chúng
ta
có
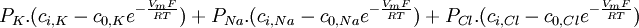 (3.35)
(3.35)
Nhân
với
hệ
số
thấm
màng
và
tổng
hợp
lại
ta
có
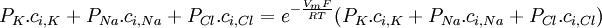 (3.36)
(3.36)
Từ
phương
trình
này,
chúng
ta
có
thể
tính
được
hiệu
điện
thế
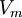 qua
màng
tế
bào
như
dưới:
qua
màng
tế
bào
như
dưới:
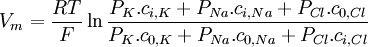 (3.37)
(3.37)
Trong
đó
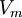 bằng
điện
thế
trog
màng
trừ
đi
điện
thế
ngoài
màng
(ví
dụ
điện
thế
chuyển
màng).
Phương
trình
này
được
gọi
la
phương
trình
Goldman-Hodgkin-Katz.
Nó
bắt
nguồn
dựa
trên
công
sức
của
David
Goldman
(1943)
và
Hodgkin,
Katz
(1949).
Lưu
ý
đầu
tiên
trong
phương
trình
3.37
là
đóng
góp
tỉ
đối
của
mỗi
ion
đặc
biệt
với
điện
thế
nghỉ
là
tương
đối
bởi
sự
thấm
của
các
ion
này.
Với
sợi
trục
mực
ống,
chúng
ta
chú
ý
rằng
(
phần
3.5.2)
bằng
điện
thế
trog
màng
trừ
đi
điện
thế
ngoài
màng
(ví
dụ
điện
thế
chuyển
màng).
Phương
trình
này
được
gọi
la
phương
trình
Goldman-Hodgkin-Katz.
Nó
bắt
nguồn
dựa
trên
công
sức
của
David
Goldman
(1943)
và
Hodgkin,
Katz
(1949).
Lưu
ý
đầu
tiên
trong
phương
trình
3.37
là
đóng
góp
tỉ
đối
của
mỗi
ion
đặc
biệt
với
điện
thế
nghỉ
là
tương
đối
bởi
sự
thấm
của
các
ion
này.
Với
sợi
trục
mực
ống,
chúng
ta
chú
ý
rằng
(
phần
3.5.2)
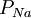 /
/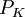 =
0.04,
điều
đó
giải
thich
tại
sao
điện
thế
nghỉ
là
gần
tương
đối
với
=
0.04,
điều
đó
giải
thich
tại
sao
điện
thế
nghỉ
là
gần
tương
đối
với
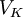 và
khác
xa
với
và
khác
xa
với
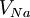 .
.
Thay nhiệt độ 37 °C và logarit Napier, phương trình 3.37 có thể được viết lại thành
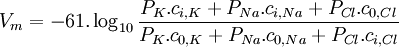 (3.38)
(3.38)
Ví
dụ
Ta
có
thể
dễ
dàng
biểu
diễn
phương
trinh
Goldman-Hodgkin-Katz
(phương
trình
3.37)
quy
về
phương
trình
Nernst
(phương
trình
3.21).
Giả
sử
rằng,
nồng
độ
ion
clo
ở
cả
tron
và
ngoài
màng
bằng
0
(i.e.,
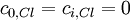 ),
khi
đó,
một
phần
ba
tử
số
và
mẫu
số
trong
phương
trình
3.37
sẽ
thiếu.
Giả
sử
xa
hơn
một
chút
rằng
tính
thấm
với
natri
(thường
là
rất
nhỏ)
chính
xác
bằng
0.
Dưới
điều
kiện
của
phương
trình
Goldman-Hodgkin-Katz,
ta
có
thể
rút
gọn
về
dạng
của
phương
tình
Nernst
(chú
ý
rằng
giá
trị
tuyệt
đối
của
hóa
trị
của
ion
trong
câu
hỏi
|z|
=
1).
Sự
chứng
minh
lại
này
thể
hiện
rằng
phương
trình
Nernst
thể
hiện
hiệu
điện
thế
cân
bằng
qua
ion
thấm
của
màng
tế
bào
với
hệ
thống
chứa
chỉ
một
ion
thấm.
),
khi
đó,
một
phần
ba
tử
số
và
mẫu
số
trong
phương
trình
3.37
sẽ
thiếu.
Giả
sử
xa
hơn
một
chút
rằng
tính
thấm
với
natri
(thường
là
rất
nhỏ)
chính
xác
bằng
0.
Dưới
điều
kiện
của
phương
trình
Goldman-Hodgkin-Katz,
ta
có
thể
rút
gọn
về
dạng
của
phương
tình
Nernst
(chú
ý
rằng
giá
trị
tuyệt
đối
của
hóa
trị
của
ion
trong
câu
hỏi
|z|
=
1).
Sự
chứng
minh
lại
này
thể
hiện
rằng
phương
trình
Nernst
thể
hiện
hiệu
điện
thế
cân
bằng
qua
ion
thấm
của
màng
tế
bào
với
hệ
thống
chứa
chỉ
một
ion
thấm.
3.4.3 Điện thế nghịch
Điện
thế
màng
mà
mà
tại
đó
cường
độ
dòng
điện
thực
bằng
0
được
gọi
là
điện
thế
nghịch.
Kí
hiệu
này
xuất
phát
từ
thực
tế
khi
điện
thế
màng
tế
bào
bị
tăng
lên
hoặc
giảm
đi....khi
màng
tế
bào
cho
thấm
qua
hai
dạng
ion
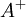 và
và
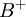 và
tỉ
lệ
thấm
của
các
ion
này
là
và
tỉ
lệ
thấm
của
các
ion
này
là
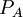 /
/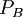 ,
điện
thế
nghị
được
xác
định
bằng
phương
trình
,
điện
thế
nghị
được
xác
định
bằng
phương
trình
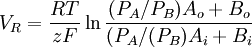 (3.39)
(3.39)
Phương
trình
này
tương
tự
như
phương
trình
Nenst
(3.21),
nhưng
nó
gồm
hai
dạng
ion.
Đây
là
dạng
đơn
giản
nhất
của
phương
trình
Goldman-Hodgkin-Katz
(phương
trình
3.37).
3.5 Dòng ion qua màng
3.5.1 Sự dịch chuyển của các hệ số ion khi qua màng
Trong phần này, ta sẽ khảo sát sự thay đổi của dòng ion qua màng tế bào dưới điều kiện nghỉ thông thường. Dòng ion này qua màng tế bào phụ thuộc vào ba yếu tố:
1. Tỉ lệ của nồng độ ion trên cả hai mặt của màng tế bào
2. Điện thế qua màng và
3. Độ thấm màng
Hiệu ứng của sự chênh lệch nồng độ và điện thế màng trong dòng ion tỉ lệ với nhau, thay cho tỉ lệ nồng độ nồng độ là điện thế Nernst tương ứng được quan tâm. Lực tác động lên các ion tỉ lệ với sự chênh lệch điện thế màng và điện thế Nernst.
Về độ thấm màng, chúng tôi lưu ý rằng liệu màng sinh học chỉ gồm có hai lớp lipit như được miêu tả một cách dễ dàng không, tất cả các dòng ion có thể có trễ lớn. Tuy nhiên, các protein đặc biệt cũng có mặt, chúng đi qua màng và có chứa các kênh nước. Gống như các kênh đặc biệt với các ion đã biết, chúng cũng gồm các cổng rất nhạy với điện thế màng tế bào. Kết quả thực là độ thấm màng khác nhau với các ion khác nhau và nó cũng dễ bị tác động bởi sự thay đổi trong điện thế chuyển màng hoăc bởi một ít các phổi tử.
Như đã đề cập đến trong phần 3.4.1, Hodgkin and Huxley (1952a) đã đề ra về quan hệ định lượng được gọi là nguyên lý độc lập. Theo nguyên lí này. Dòng ion qua màng tế bào không phụ thuộc vào sự có mặt của các ion khác.
Do đó, dòng của mỗi loại ion khác nhau qua màng tế bào có thể coi như không phụ thuộc vào các dạng ion khác. Bằng cách xếp chồng, tổng cường độ dòng điện qua màng khi đó bằng tổng của các dòng do các ion khác nhau tạo nên
3.5.2 Dòng ion màng trong tế bào thần kinh vận động của mèo
Chúng ta sẽ thảo luận các phản ứng của dòng ion trong ví dụ này. Với cơ thể của mèo, nồng độ ion được đo như bảng dưới đây ( nhìn bảng 3.1)
| Nồng độ ion |
Bên
ngoài
màng
[mol/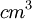 ] ] |
Bên
trong
màng
[mol/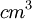 ] ] |
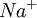 |
150 | 15 |
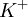 |
5.5 | 150 |
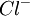 |
125 | 9 |
Với mỗi ion, điện thế cân bằng ở dưới có thể tính được nhờ phương trình Nernst
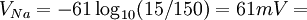
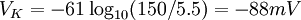
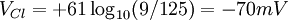
Điện thế nghỉ của tế bào đo được là -70mV
Bây giờ, chúng ta sẽ nghiên cứu các phần tử ion khác nhau một cách chi tiết hơn. Hodgkin and Huxley đã mô tả các thuộc tính dòng điện của sợi trục bắt đầu từ những năm 1950 (xem chương 4), họ tin rằng hai đến ba dạng kênh ion khác nhau (Na+, K+, and Cl-) là đầy đủ với thuộc tính của trạng thái tế bào kích thích. Tuy nhiên, số các kênh ion khác nhau là rất lớn. Vào năm 1984, , Bertil Hille (Hille, 1984/1992) đã tổng kết lại những gì mà ông ấy biết vào thời gian này về kênh ion. Ông ấy quan tâm tới bốn đến năm dạng kênh ion cùng có trong tế bào và gen có mã là tổn của 50 kênh khác nhau. Hiện nay, điều đó được tin tưởng rằng mỗi tế bào khác nhau đều có it nhât 50 kênh ion khác nhau và số kênh protein khac nhau đạt đến khaỏng 1000
Ion
Clo
Trong ví dụ này, điện thế cân bằng của ion clo giống như điện thế nghỉ của màng tế bào. Trong khi điều này không phải là trường hợp thông thường, sự thật là điện thế Nernst của clo không giống như điện thế nghỉ. Điều kiện này xảy ra bởi vì nồng độ ion clo tương đối cao, thậm chí sự di chuyển nhỏ trong hoặc ngoài màng sẽ là cho kênh thay đổi lớn. Vì vậy, tỉ lệ nồng độ, theo điện thế Nernst, phụ thuộc vào sự thay đổi của điện thế nghỉ cân bằng.
Ion
Kali
Trong ví dụ được mô tả ở trong bảng 3.1, điện thế cân bằng của ion kali la 19mV âm hơn điện thế nghỉ của tế bào. Trong phần sau, chúng ta sẽ giải thích rằng đây là kết quả điển hình và điện thế nghỉ luôn vượt quá điện thế Nernst của kali. Do đó, chúng ta luôn mong đợi rằng dòng ion thực của ion kali từ trong dến ngoài màng tế bào đưới điều kiện nghỉ. Để bù cho dòng này, và bằng cách duy trì kết cấu ion thông thường, ion kali cũng không được di chuyển trong màng. Tuy nhiên, sự di chuyển như vậy trong theo hướng điện thế tăng yêu cầu sử dụng năng lượng. Đó là với điều kiện bơm NA-K hoạt động di chuyển ion kali có hại cho năng lượng.
Ion
Natri
Điện thế cân bằng của ion natri là +61mV, nó được tính từ tỉ lệ nồng độ (bảng 3.1). Do đó, trạng thái cân bằng của ion natri là 131mV và dòng natri ( có đượ ở cả hai lực khuyếch tán và lực điện trường) sẽ xảy ra ở trạng thái nghỉ. Rõ ràng cả kali và natri không đạt cân bằng nhưng điều kiện nghỉ yêu cầu chỉ một trạng thái ổn định. Đặc biệt, tổng cường độ dòng điện màng phải bằng 0. Với natri và kali, điều đó cũng có nghĩa là tổng các dòng trong và ngoài phải bằng nhau về độ lớn. Khi lực truyền với kali lớn gấp 6.5 lần natri. Bởi vì, độ thấm nghỉ yếu nên sự đóng góp của ion natri với điện thế chuyển màng nghỉ thi thoảng không được nhắc đến như xấp xỉ. Trong ví dụ ở trên, nồng độ và độ thấm ion được chọn cho tế bào thần kinh vận động của mèo. Trong sợi trục của mực ống, tỉ lệ của độ thấm màng nghỉ của kali, natri và clo là
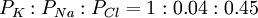
3.5.3 Bơm Na-K
Với cấu trúc của các ion của không gian trong và ngoài màng tế bào được duy trì bởi bơm Na-K. Giống như chú ý ở trên, trong trạng thái ổn định, tổng cường độ các dòng điện bị động bằng 0. Dòng ngoài và dòng trong của kali bằng nhau và ngược dấu (khi chúng cùng có thành phần ion). Khi bơm Na-K được tin rằng sẽ trao đổi 1 mol kali cho 1 mol natri, không có dòng điện thực nào được mong đợi ở đây. Tuy nhiên, những chứng minh mới đây cho thấy bới 2 mol kali bơm vào sẽ cho ra 3 mol natri. Một cái bơm như vậy được gọi là gien điện tử và nó phải xét đến trong bất kì một kiểu về lượng nào của cường độ dòng tế bào (Junge 1981)
3.5.4 Hình minh họa của dòng ion màng tế bào
Dòng ion của natri và kali qua màng tế bào và gradient điện hóa được minh họa trong hinh 3.5. Với mỗi ion, các sợi rõ ràng miêu tả các dòng ion, độ rộng của viền và số lượng của dòng và độ dốc, độ bền của gradient điện hóa. Như trong hình 3.2, trục tung chỉ ra điện thế và trục hoàng là khoảng các thông thường tới màng. Hơn nữa, ΔV dương (hướng xuống), cường độ dòng chuyển màng (với ion dương) cũng dương (vi dụ hướng ra phía ngoài). Với ion âm clo, nó sẽ hướng vào trong.
Hìn 3.5. Một dạng minh họa dòng ion chuyển màng (After Eccles, 1968.)
Chú ý rằng với dòng ion bị động K+ and Cl- dưới tác dụng của khuyếch tán và điện trường được chỉ ra một cách riêng rẽ)
3.6 Phương trình cáp của sợi trục
Ludvig Hermann (1905b) là người đầu tiên đưa ra rằng dưới điều kiện dưới ngưỡng, màng tế bào có thể được mô tả bởi điện trở thoát và tụ mắc song song phân bố đồng thời. Do đó, phản ứng của kich thích dòng điện bất kì có thể được tính từ sự chế tạo của nguyên lý mạch điện. Trong phần này, chúng tôi sẽ minh họa cách tiếp cận trong tế bào, nó là một dạnh hình trụ tròn với độ dài lớn hơn rất nhiều so với bán kính. (mô hình này được áp dụng cho sợi trục thần kinh unmyelinated)
3.6.1 Mô hình cáp của sợi trục
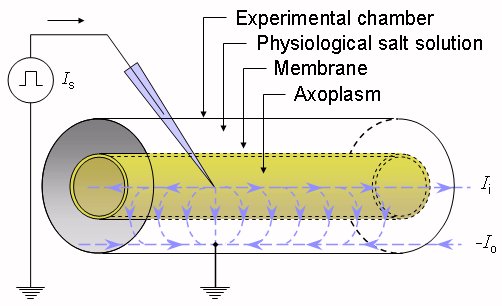
Giả sử rằng, sợi trục là được ngâm trong chất điện phân có quy mô xác định (hinh dung như môi trường ngoại bào) và xung điện kích thích được đưa vào qua hai điện cực, một xác định sơi trục ngoài trong môi trương ngoại bào và một là sợ trục bên trong như minh họa ở hinh 3.6. Tổng cường độ dòng kích thích (Ii) quanh trục trong của sơi trục sẽ giảm theo khoảng cách từ một phần qua liên tục màng tế bào để trở lại cường độ dòng ngoài sợi trục. Chú ý rằng, sự xác định hướng của các dòng dương là bên phải với Ii và Io trong trường hợp sự bảo toàn của dòng yêu cầu là Io = -Ii. Đồng thời giả sử rằng cả trong và ngoài của sợi trục, điện thế không thay đổi khi đi bất kì phần nào (không phụ thuộc vào hướng của dây thần kinh quay) và hệ thống này thể hiện một trục đối xứng. Sự gần đúng này được dựa trên kích thước mặt cắt, nó có thể rất nhỏ so với độ dài của miền hoạt động của sợi trục. Nếu như cũng cho rằng độ dài của sợi trục là lớn hơn cái giả định thì nó hầu như là không xác định.
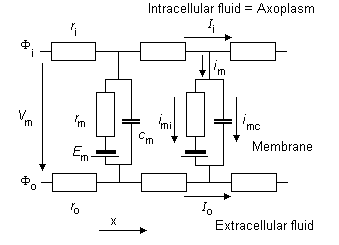
Dưới các giả định này, mạch tương đương của hình 3.7 có thể mô tả sợi trục. Một điều đặc biệt nên chú ý là không gian gian ngoại bào bị giới hạn trong hình 3.6 quanh hướng ngang và do đó, nó đảm bảo cho việc gán điện trở ngang Ro để biểu diễn dung dịch giữa các nút. Trong mô hình này, mỗi phần mà biểu diễn thành phần ngang của sợi trục trong với biên của dung dịch ngoại bào được chọn ngắn hơn so với tổng chiều dài sợi trục. Chú ý, đặc biệt là màng dưới ngưỡng được thể hiện như một điện trở phân tán và tụ điện mắc song song. Linh kiện điện trở cũng quan tâm đến cường độ dòng điện ion màng imI, điện trở phản ánh một sự thực rằng màng là một dây dẫn kém nhưng là một chất điện môi tốt và do đó, cường độ điện dung màng imC phải bao gồm cả các linh kiên của dòng màng tổng. Các đường nội và ngoại bào ngang đều có điện trở, nó phản ánh những bằng chứng thí nghiệm về sợi trục thần kinh.
Hình 3.6. Thiết bị thí nghiệm cho sự hình thành phương trình cáp sợi trục
Hình 3.7 Mô hình mạch điện tương đương của sợi trục. Một chứng minh cho các linh kiện được đưa ra trong đoạn văn trên.
Các linh kiên của mạch tương đương được miêu tả trong hình 3.7 bao gồm các thành phần dưới đây: chú ý rằng thay cho đơn vị MKS, kích thước được cho ở đây là đơn vị truyền thốn được dùng cho các liên kết này. Cũng lưu ý thêm là khối lượng thể hiện trên một đơn vị chiều dài được viết với các kí tự nhỏ.
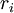 =
điện
trở
hướng
trục
nội
bào
của
bào
tương
sợi
trục
trên
một
đơn
vị
chiều
dài
sợi
trục
[kΩ/cm
sợi
trục]
=
điện
trở
hướng
trục
nội
bào
của
bào
tương
sợi
trục
trên
một
đơn
vị
chiều
dài
sợi
trục
[kΩ/cm
sợi
trục]
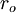 =
điện
trở
hướng
trục
ngoại
bào
của
môi
trường
ngoại
bào
trên
một
đơn
vị
chiều
dài
sợi
trục
[kΩ/cm
sợi
trục]
=
điện
trở
hướng
trục
ngoại
bào
của
môi
trường
ngoại
bào
trên
một
đơn
vị
chiều
dài
sợi
trục
[kΩ/cm
sợi
trục]
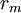 =
điện
trở
màng
nhân
với
đơn
vị
chiều
dài
của
sợi
trục
[kΩ.cm
sợi
trục]
(chú
ý
rằngđay
là
theo
hướng
tâm
)
=
điện
trở
màng
nhân
với
đơn
vị
chiều
dài
của
sợi
trục
[kΩ.cm
sợi
trục]
(chú
ý
rằngđay
là
theo
hướng
tâm
)
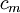 =
điện
dung
mangf
trên
một
đơn
vị
chiều
dài
sợi
trục
[
=
điện
dung
mangf
trên
một
đơn
vị
chiều
dài
sợi
trục
[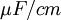 sợi
trục]
sợi
trục]
Chúng
ta
xác
định
cường
độ
dòng
điện
và
điện
thế
của
mạch
như
ở
dưới
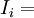 tổng
cường
độ
dòng
điện
trong
nội
bào
theo
chiều
dọc
tổng
cường
độ
dòng
điện
trong
nội
bào
theo
chiều
dọc
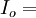 tổng
cường
độ
dòng
điện
trong
ngoại
bào
theo
chiều
dọc
tổng
cường
độ
dòng
điện
trong
ngoại
bào
theo
chiều
dọc
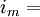 tổng
cường
độ
dòng
điện
chuyển
màng
trên
một
đơn
vị
chiều
dài
sợi
trục
[μA/cm
sợi
trục]
tổng
cường
độ
dòng
điện
chuyển
màng
trên
một
đơn
vị
chiều
dài
sợi
trục
[μA/cm
sợi
trục]
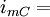 tổng
cường
độ
dòng
điện
chuyển
màng
trên
một
đơn
vị
chiều
dại
sợi
trục
[μF/cm
sợi
trục]
tổng
cường
độ
dòng
điện
chuyển
màng
trên
một
đơn
vị
chiều
dại
sợi
trục
[μF/cm
sợi
trục]
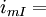 thành
phần
điện
dung
của
dòng
chuyểnmàng
trên
một
đơn
vị
trên
một
đơn
vị
chiều
dại
sợi
trục
[μF/cm
sợi
trục]
thành
phần
điện
dung
của
dòng
chuyểnmàng
trên
một
đơn
vị
trên
một
đơn
vị
chiều
dại
sợi
trục
[μF/cm
sợi
trục]
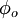 =
điện
thế
ngoài
màng
tế
bào
[mV]
=
điện
thế
ngoài
màng
tế
bào
[mV]
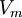 =
=
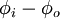 điện
thế
màng
điện
thế
màng
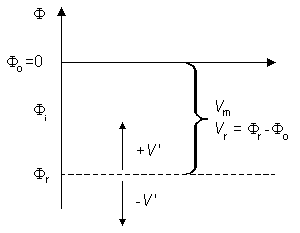
V'
=
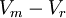 độ
lệch
của
điện
thế
màng
ở
trạng
thái
nghỉ
độ
lệch
của
điện
thế
màng
ở
trạng
thái
nghỉ
Các
hình
vẽ
phác
họa
điện
thế
khác
nhau
và
điện
thế
trong
sợi
trục
đua
ra
trong
hình
3.8
Chúng
ta
chú
ý
rằng
hướng
của
các
dòng
dương
được
xác
định
như
hướng
dương
của
trục
x
trong
và
ngoài
sợi
trục.
Do
đó,
với
tất
cả
các
giá
trị
cỉa
x,
sự
bảo
toàn
dòng
điện
yêu
cầu
là
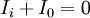 miễn
là
x
không
bị
sai
giữa
các
điện
cự
kịc
thích.
Với
miền
sai
giữa
các
điện
cực,
miễn
là
x
không
bị
sai
giữa
các
điện
cự
kịc
thích.
Với
miền
sai
giữa
các
điện
cực,
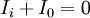 phải
bằng
cường
độ
dòng
điện
đặt
vào
thực.
phải
bằng
cường
độ
dòng
điện
đặt
vào
thực.
Hình 3.8 Hình phác họa mô tả hiệu số điện thế và điện thế trong của sợi trục trong cuốn sách.
Trong
trường
hợp
đặc
biệt
khi
không
có
dòng
kích
thích
(ví
dụ,
khi
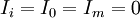 ),
khi
Vm
=
Vr
và
V'
=
0).
Tuy
nhiên,
sự
hoạt
hóa
mới
bắt
đầu,
chúng
ta
sẽ
thấy
được
có
khả
năng
),
khi
Vm
=
Vr
và
V'
=
0).
Tuy
nhiên,
sự
hoạt
hóa
mới
bắt
đầu,
chúng
ta
sẽ
thấy
được
có
khả
năng
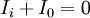 ở
mọi
nơi
và
V'
≠
0
trong
vùng
đã
biết.
ở
mọi
nơi
và
V'
≠
0
trong
vùng
đã
biết.
Trong đó Vr , điện thế màng nghỉ giồng nhau ở moi nơi, nó được tính bằng
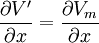 và
và
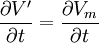 (3.40)
(3.40)
dựa trên cách xác định V' ở trên.
3.6.2 Đáp ứng ổn định
Đầu tiên chúng ta sẽ quan tâm tới trường hợp cố đinh (ví dụ δ/δt = 0), nó là điều kiện trạng thái ổn định đạt được theo ứng dụng các bước của dòng điện. Sự tương ứng này khi t . Đáp ứng trạng thái nghỉ được minh họa trong hình 3.9. nó tuân theo định luật Ohm
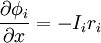 ,
,
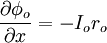 (3.41)
(3.41)
Từ định luật bảo toàn dòng điện sinh ra dòng chuyển màng trên một đơn vị chiều dài im, nó quan hệ với dòng suy giảm của Ii hoặc dòng tăng ích:
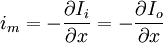 (3.42)
(3.42)
Chú
ý
rằng
phương
trình
này
thỏa
mãn
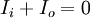 .
từ
điều
kiện
và
phương
trình
3.40,
3.41
(
đặt
V’
=
Φi
-
Φo
-
Vr
)
ta
được
.
từ
điều
kiện
và
phương
trình
3.40,
3.41
(
đặt
V’
=
Φi
-
Φo
-
Vr
)
ta
được
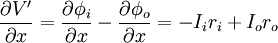 (3.43)
(3.43)
Ngoài ra, bằng cách lấy đạo hàm với x, ta có
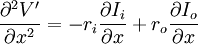 (3.44)
(3.44)
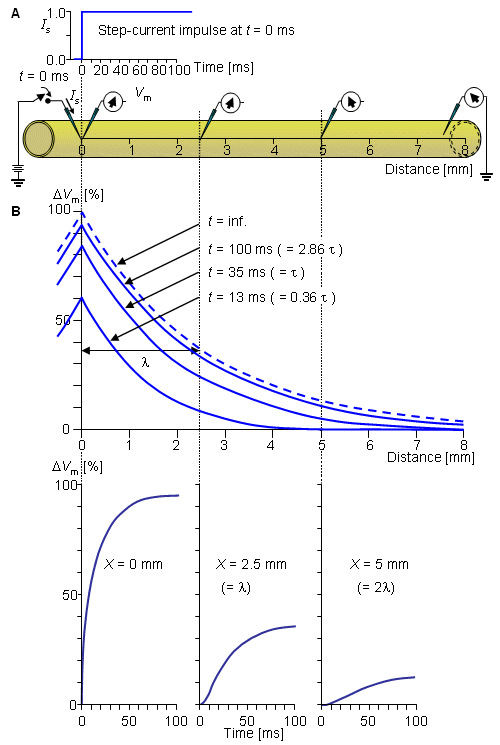
Hình. 3.9. (A) Kích thích của dây thần kinh với bậc dòng điện. (B) Sự biến đổi của điện thế màng như là một hàm của khoảng cách
Thay thế 3.42 vào phương trình 3.44 ta được
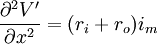 (3.45)
(3.45)
nó
được
gọi
là
phương
trình
cáp
thông
thường
Dưới
điều
kiện
cố
định
và
ngưỡng,
cường
độ
dòng
điện
điện
dung
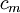 dV'/dt
=
0;
cường
độ
dòng
điện
màng
trên
một
đơn
vị
chiều
dài
chỉ
đơn
giản
bằng
dV'/dt
=
0;
cường
độ
dòng
điện
màng
trên
một
đơn
vị
chiều
dài
chỉ
đơn
giản
bằng
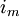 =
V'/
=
V'/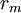 ;
theo
định
luật
Ohm.
Do
đó,
phương
trình
3.45
có
thể
viết
lại
thành
;
theo
định
luật
Ohm.
Do
đó,
phương
trình
3.45
có
thể
viết
lại
thành
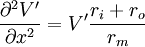
Kết quả của nó là
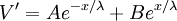 (3.47)
(3.47)
Hằng số λ trong phương trình 3.47 có đơn vị là chiều dàu và nó được gọi là độ dài đặc trưng hoặc hằng số dài của sợi trục. Nó cũng được gọi là hệ số khoảng cách. Độ dài đặc trưng λ trong phương trình 3.46 được tính bằng:
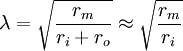 (3.48)
(3.48)
Đây
là
dạng
cuối
của
phương
trình
3.48
bởi
vì
điện
trở
trục
ngoại
bào
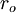 nhỏ
hơn
rất
nhiều
so
với
điện
trở
trục
nội
bào
nhỏ
hơn
rất
nhiều
so
với
điện
trở
trục
nội
bào
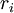
Với điều kiện biên
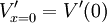 và
và
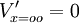
hằng số A và B thỏa mãn giá trị A = V'(0) và B = 0, và từ phương trình 3.47 chúng ta có kết quả
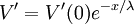
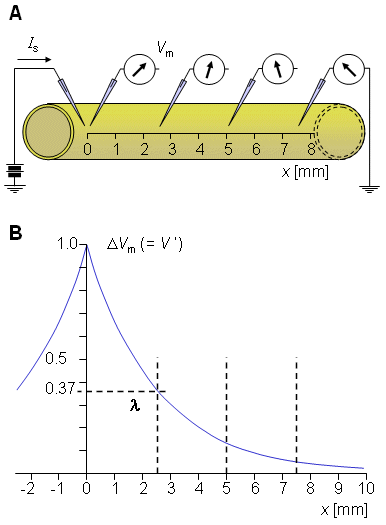
Biểu thức chỉ ra rằng V' giảm theo hàm mũ từ đầu sợi trục thần kinh tại điểm kích thích (x=0) như hình 3.9B. tại x = λ, biên độ giảm đi 36.8% so với giá trị gốc. Do đó, λ là giá trị của khoảng cách từ vị trí kích thích trên đáp ứng đáng kể đạt được. Ví dụ tại x = 2 λ, đáp ứng giảm đi 13.5% trong khi x =5 λ nó chỉ còn 0.7% giá trị gốc.
3.6.3 Kích thích với xung dòng điện
Trong phần này chúng tôi quan tâm đến đáp ứng tạm thời (nhanh hơn trạng thái ổn định) đến một đầu vào bước dòng dưới ngưỡng. Trong trường hợp này dòng màng tế bào được bao gồm cả hai thành phần điện trở và tụ điện phản ánh bản chất RC song song của màng tế bào:
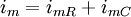 (3.50)
(3.50)
ở đây:
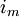 =
tổng
dòng
màng
tế
bào
trên
mỗ
đơn
vị
chiều
dài
[
A/cm
chiều
dài
sợi
trục]
=
tổng
dòng
màng
tế
bào
trên
mỗ
đơn
vị
chiều
dài
[
A/cm
chiều
dài
sợi
trục]
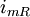 =
thành
phần
điện
trở
của
dòng
màng
trên
mỗi
dơn
vị
độ
dài
[
=
thành
phần
điện
trở
của
dòng
màng
trên
mỗi
dơn
vị
độ
dài
[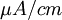 chiều
dài
sợi
trục]
chiều
dài
sợi
trục]
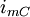 =
thành
phần
tụ
của
dòng
màng
trên
mỗi
đơn
vị
chiều
dài
[
=
thành
phần
tụ
của
dòng
màng
trên
mỗi
đơn
vị
chiều
dài
[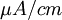 chiều
dài
sợi
trục]
chiều
dài
sợi
trục]
Dưới điều kiện tạm thời phương trình 3.50 thế vào 3.45 có thể được viết:
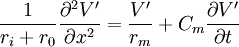 (3.51)
(3.51)
Có thể dễ dàng thể hiện như
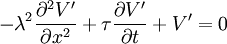 (3.52)
(3.52)
ở
đây
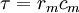 là
thời
gian
không
đổi
của
màng
tế
bào
và
là
thời
gian
không
đổi
của
màng
tế
bào
và
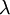 là
không
gian
không
đổi
như
được
định
nghĩa
trong
phương
trình
3.48
Ở
đây
thời
gian
không
đổi
được
lấy
từ
cho
một
khoảng,
sự
phù
hợp
của
sợi
cơ
mỏng
với
một
vấn
đề
kích
thước.
Thời
gian
không
đổi
có
thể
được
lấy
với
một
phương
pháp
tương
tự
cho
mặt
phẳng
của
màng
như
một
vấn
đề
hai-kích
thước.
Trong
trường
hợp
thay
vì
sử
dụng
biến
được
định
nghĩa
“lần
đơn
vị
chiều
dài”
và
“
trên
mỗi
đơn
vị
chiều
dài”,
biến
được
định
nghĩa
“
lần
đơn
vị
diện
tích”
và
“trên
mỗi
đơn
vị
diện
tích”
được
sử
dụng.
Sau
đó
chúng
tôi
thu
được
cho
thời
gian
không
đổi
là
không
gian
không
đổi
như
được
định
nghĩa
trong
phương
trình
3.48
Ở
đây
thời
gian
không
đổi
được
lấy
từ
cho
một
khoảng,
sự
phù
hợp
của
sợi
cơ
mỏng
với
một
vấn
đề
kích
thước.
Thời
gian
không
đổi
có
thể
được
lấy
với
một
phương
pháp
tương
tự
cho
mặt
phẳng
của
màng
như
một
vấn
đề
hai-kích
thước.
Trong
trường
hợp
thay
vì
sử
dụng
biến
được
định
nghĩa
“lần
đơn
vị
chiều
dài”
và
“
trên
mỗi
đơn
vị
chiều
dài”,
biến
được
định
nghĩa
“
lần
đơn
vị
diện
tích”
và
“trên
mỗi
đơn
vị
diện
tích”
được
sử
dụng.
Sau
đó
chúng
tôi
thu
được
cho
thời
gian
không
đổi
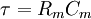 .
.
Những
đáp
ứng
thời
gian
và
không
gian
của
điện
thế
màng
tế
bào
cho
một
số
giá
trị
đặc
điểm
của
x
và
t
được
minh
họa
trong
hình
3.10.
Nên
chú
ý
rằng
hoạt
động
của
V’
như
một
hàm
của
x
là
hàm
mũ
cho
tất
cả
giá
trị
của
t,
nhưng
đáp
ứng
như
một
hàm
của
t
cho
nhiều
giá
trị
lớn
của
x
khác
nhiều
với
hoạt
động
hàm
mũ
(trở
thành
dạng
S).
Những
đường
cong
đó
được
minh
họa
trong
sự
giải
thích
của
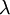 ,
không
gian
cố
định,
như
một
phép
đo
của
phạm
vi
không
gian
của
đáp
ứng
với
dòng
kích
thích.
Với
giá
trị
của
,
không
gian
cố
định,
như
một
phép
đo
của
phạm
vi
không
gian
của
đáp
ứng
với
dòng
kích
thích.
Với
giá
trị
của
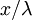 nhỏ
hơn
2,
nhỏ
hơn
2,
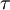 cơ
bản
là
một
phép
đo
thời
gian
để
thu
được
trạng
thái
ổn
định.
Tuy
nhiên,
với
cơ
bản
là
một
phép
đo
thời
gian
để
thu
được
trạng
thái
ổn
định.
Tuy
nhiên,
với
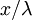 lớn
sự
giải
thích
này
trở
thành
không
chính
xác
vì
đường
cong
tạm
thời
lệch
nhiều
từ
hàm
mũ.
Trong
hình
3.10,
ở
chỗ
lớn
sự
giải
thích
này
trở
thành
không
chính
xác
vì
đường
cong
tạm
thời
lệch
nhiều
từ
hàm
mũ.
Trong
hình
3.10,
ở
chỗ
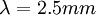 điện
cực
tại
x
=
5
mm
là
điện
cực
tại
x
=
5
mm
là
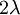 ,
và
biên
độ
,
sau
một
khoảng
thời
gian
,
và
biên
độ
,
sau
một
khoảng
thời
gian
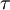 ,
chỉ
đạt
tớ
37%
của
trạng
thái
ổn
định.
Ví
dụ,
x
=
25mm
(tương
đương
với
,
chỉ
đạt
tớ
37%
của
trạng
thái
ổn
định.
Ví
dụ,
x
=
25mm
(tương
đương
với
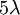 ),
chỉ
0.8%
trạng
thái
ổn
định
sẽ
đạt
được
sau
khoảng
thời
gian
),
chỉ
0.8%
trạng
thái
ổn
định
sẽ
đạt
được
sau
khoảng
thời
gian
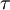 .
.
(A) khởi tạo vật lý, bao gồm dạng sóng của dòng cung cấp và vị trí của điện cực kích thích và điện cực ghi
(B)
Đáp
ứng
không
gian
tại
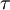 =
13,
35,
100
ms;
và
t
=
.
Đường
cong
cuối
cùng
là
đáp
ứng
trạng
thái
ổn
định
và
thành
phần
cho
biểu
thức
3.49
=
13,
35,
100
ms;
và
t
=
.
Đường
cong
cuối
cùng
là
đáp
ứng
trạng
thái
ổn
định
và
thành
phần
cho
biểu
thức
3.49
(C) Đáp ứng tạm thời của ba phía trục tại x = 0, 2.5, 5 mm.
Trong
khi
một
đáp
án
dạng
gần
cho
biểu
thức
3.53
có
thể
được
mô
tả,
chúng
tôi
đã
từng
chọn
để
loại
bỏ
nó
từ
bài
này
vì
tính
phức
tạp
của
nó.
Có
thể
tìm
thấy
nguồn
gốc
trong
Davis
and
Lorente
de
No
(1947).
Thay
vì
bao
gồm
tài
liệu
phân
tích
này,
chúng
tôi
đã
từng
chọn
thay
thế
để
minh
họa
đáp
ứng
thời
gian
và
không
gian
của
điện
thế
màng
vận
chuyển
cho
một
nhịp
dòng
cho
một
giá
trị
lớn
của
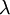 và
và
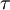 .
Điều
này
được
cung
cấp
trong
hình
3.11
.
Điều
này
được
cung
cấp
trong
hình
3.11
Đặc biệt, hình 3.11 mô tả đáp ứng điện thế dưới ngưỡng cho một nhịp dòng của khoảng thời gian được giới thiệu bên ngoài màng tại trung tâm của một cap có chiều dài hữu hạn. Những đáp ứng, khi dòng đượ bật lên,đựoc chỉ ra ở bên trái của hình vẽ, trong khi đáp ứng, khi dòng bị tắt đi ở vế phải. Điện thế màng vận chuyển được mô tả như một hàm thời gian cho những vị trí nhất định của sợi. Nó cũng được mô tả như một hàm của vị trí tại thời gian đưa vào theo sau ứng dụng của dòng hoặc thiết bị ngoài của nó. Hình vẽ được vẽ từ một sự tính toán lại của chất lượng của nó từ những công bố ban đầu của Hodgkin and Rushton (1946).
Chú ý rằng khoảng cách được chỉ ra chuẩn hóa cho không gian cố định, trong khi thời gian được chuẩn hóa cho thời gian cố định. Việc chuẩn hóa, như ở đây , dẫn đến trong đường cong tổng quát mà có thể được chuyển cho bất kì giá trị thực tế nào. Chú ý rằng những điểm trên một điện thế riêng biệt chống lại đường cong khỏang cách đựoc vẽ tại một vài giá trị của t trong biểu đồ dưới cũng có thể được tìm thấy tại những giá trị giống nhau của t trong đồ thị thấp hơn cho giá trị khoảng cách riêng, và ngược lại. Thực tế là đường cong cao hơn và thấp hơn chỉ ra hiện tượng giống nhau nhưng trong sự khác nhau về kích thước được nhấn mạnh bởi đường dọc chấm cách mà chỉ ra vị trí phù hợp của điểm trong hai đường cong.
Bảng 3.2 liệt kê các giá trị được đo của chiều dài đặc trưng và thời gian không đổi cho một vài sợi trục cho những hình dạng khác nhau được nhìn thấy.
Bảng3.2Cable constants for unmyelinated axons of different species
|
Các
hình
dạng
|
|||||
| Đại lượng | Đơn vị | Mực | Tôm hùm | Tôm | |
| Đường kính |
![\left[\mu m\right]](https://tusach.thuvienkhoahoc.com/images/math/3/a/f/3af37a1b2567978e47cab7fd0f765995.png) |
500 | 75 | 50 | |
Chiều
dài
đặc
trưng
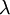
|
[cm] | 0.5 | 0.25 | 0.25 | |
| Hằng số thời gian | [ms] | 0.5 | 0.25 | 0.25 | |
| Điện trở đặc trưng của màng*) |
![\left[k\Omega \cdot cm^{2}\right]](https://tusach.thuvienkhoahoc.com/images/math/a/4/a/a4a52ec8f0b6165420ce46fc3fa71738.png) |
0.7 | 2.0 | 5.0 |
*)Điển trở và điện dung đặc trưng của màng có thể được tính từ các giá trị của điện trở và điện dung theo công thức sau:
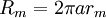 (3.54)
(3.54)
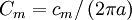 (3.55)
(3.55)
ở đây:
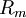 =
điện
trở
đặc
biệt
của
màng
tế
bào
=
điện
trở
đặc
biệt
của
màng
tế
bào![\left[k\Omega cm^{2}\right]](https://tusach.thuvienkhoahoc.com/images/math/9/6/3/963052676147345d70553eb71c3e7c5e.png)
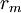 =
điện
trở
màng
nhân
đơn
vị
chiều
dài
[
=
điện
trở
màng
nhân
đơn
vị
chiều
dài
[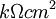 chiều
dài
sợi
trục]
chiều
dài
sợi
trục]
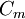 =
điện
dung
đặc
biệt
của
màng
[µF/cm²]
=
điện
dung
đặc
biệt
của
màng
[µF/cm²]
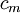 =
điện
dung
màng
trên
mỗi
đơn
vị
chiều
dài
[µF/cm
chiều
dài
sợitrục]
=
điện
dung
màng
trên
mỗi
đơn
vị
chiều
dài
[µF/cm
chiều
dài
sợitrục]
a=bán kính cáp [cm]
Hình 3.11:Đáp ứng điện thế màng tế bào dưới với một dòng nhịp của thời gian dài tại những trường hợp khác nhau của thời gian ( biểu đồ trên) và tại những khoảng cách khác nhau (biểu đồ dưới) . Đáp ứng khi dòng được bật lên và tắt đi được chỉ ra ở phía trái và phải của hình, một cách tương ứng
3.7 Mối liên hệ giữa thời gian và độ bền
Khi một màng dễ bị kích thích không được phân cực bởi dòmg kích thích mà độ lớn của nó được tăng lên một cách từ từ, một mức độ dòng sẽ được chạm tới, được gọi là ngưỡng, khi màng tế bào tồn tại một xung hoạt động. Sau đó được đặc trưng bởi sự thay đổi nhanh và ngắn trong tính thấm của màng , và được kết hợp với điện thế màng vận chuyển. Một minh họa của quá trình này được đưa ra ở hình 2.8, nơi mà đáp ứng kích thích mức 2 là dưới ngưỡng, trong khi mức 3 vừa mới xuất hiện tại ngưỡng (vì thỉnh thoảng một thế hoạt động (3B) đạt tới trong khi tại những thời gian khác một đáp ứng bị động (3A) được quan sát). Một thế hoạt động cũng được mang đến một cách rõ ràng cho kích thích chuyển ngưỡng của 4.
Khi
màng
kích
thích
bị
khử
phân
cực
Dưới điều kiện hoạt động màng không còn có thể được đặc trưng là tuyến tính, và mô hình RC được mô tả trong phần trước không thể áp dụng được. Trong chương tới, chúng tôi trình bày một nghiên cứu chi tiết về màng hoạt động.
Một kết nối giữa chương này, được giới hạn cho màng thụ động, và tiếp đó, bao gồm màng phi tuyến, nằm trong mô hình của điều kiện mà dẫn tới sự kích thích. Mặc dù đó chỉ là một sự gần đúng, nhưng chúng tôi có thể xem các màng vừa mới đạt tới điểm hoạt động như tuyến tính (ví dụ, thụ động). Vì thế, hoạt động của màng cùng với giới hạn này có thể được phân tích bằng sử dụng mạch điện thông thường. Trong trường hợp riêng, nếu giá trị ngưỡng được biết, thì sau đó nó sẽ trở thành có thể giải thích điều kiện dưới mà sự kích hoạt sẽ vừa mới được đạt tới. Vì sự kích hoạt chịu ảnh hưởng không chỉ bởi độ mạnh của dòng kích thích mà còn bởi thời gian của nó, kết quả là giá trị của đường cong độ lớn-độ bền mô tả sự kết hợp tối thiểu của độ lớn và thời gian cần để tạo ra sự kích hoạt (Arvanitaki, 1938), như được minh họa trong hình 2.10.
Một ví dụ đơn giản của những ý kiến này được trang bị bởi một tế bào mà một số hình cầu trong hình dạng và trong điện cực kích thích của nó được đặt trong tế bào và số khác ngoài tế bào. Chúng tôi có thể chỉ ra rằng với những tế bào có dạng hình cầu, cả không gian nội bào và ngoại bào là đẳng thế tại mộ thời điểm. Vì thế, nếu một dòng bị phóng qua giữa các điện cực, nó xuyên qua một cách thống nhất qua màng để tất cả các yếu tố của màng hoạt động giống nhau. Kết quả là, dòng điện phù hợp là một rm và cm tập trung trong mạch song song. Giá trị của rm là điện trở của màng nhân đơn vị diện tích, trong khi của cm là điện dung của màng trên mỗi đơn vị thời gian
Nếu Í làdòng kích thích trên mỗi đơn vị diện tích, sau đó từ lý thuyết mạch riêng biệt được ứng dụng cho mạch RC song song này, chúng tôi có
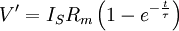 (3.56)
(3.56)
ở đây:
V' = điện tích trong điện thế màng [mV]
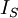 =
dòng
kích
thích
trên
mỗi
đơn
vị
thời
gian
[
=
dòng
kích
thích
trên
mỗi
đơn
vị
thời
gian
[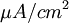 ]
]
R_m
=
điện
trở
màng
nhân
đơn
vị
diện
tích
[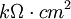 ]
]
t = thời gian kích thích [ms]
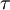 =
hằng
số
thời
gian
màng
=
=
hằng
số
thời
gian
màng
=
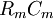 [ms]
[ms]
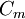 =
điện
dung
của
màng
trên
mỗi
đơn
vị
mặt
phẳng
=
điện
dung
của
màng
trên
mỗi
đơn
vị
mặt
phẳng
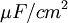 ]
]
Nhưng,
sự
phân
tích
đơn
giản
này
không
được
áp
dụng
vào
màng
tế
bào
với
các
dạng
khác
nhau,
khi
đáp
ứng
tới
cường
độ
dòng
kích
thích
theo
phương
trình
3.53
và
được
miêu
tả
trong
3.11.
Tuy
nhiên,
phương
trình
3.56
vẫ
có
thể
được
coi
như
là
xấp
xỉ
bậc
1
dựa
trên
biểu
diễn
các
biến
số
của
cấu
trúc
hằng
số
phân
phối.
Theo
sự
lập
luận
đó,
trong
hình
3.12
chúng
ta
có
thể
giả
sử
rằng
một
sợi
dài
có
thể
được
làm
xấp
xỉ
bởi
các
phần
đơn
lẻ
trước,
đo
đó,
theo
phương
trình
được
miêu
tả
trong
phương
trình
3.56.
Đáp
ứng
đặc
trưng
dựa
trên
phương
trình
3.56
cũng
được
thể
hiện
trong
hình
3.12
. Hình 3.12. Sự dẫn xuất biểu đồ thời gian
(A)Sự xấp xỉ hằng số tập trung của kênh RC, nó thay thế cho cấu trúc hằng số phân phối.
(B) Đáp ứng của kênh với xung dòng điện của đại lương Is là theo hàm số mũ và được thể hiện cho xung trong khoảng thời gian dài
Màng
được
giả
sử
được
hoạt
động
nếu
điện
thế
của
nó
đạt
giá
trị
dưới
ngưỡng.
Chúng
ta
quan
tâm
tới
điều
kiện
này
nếu
ta
thay
thế
V'=
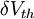 =
trong
phương
trình
3.56
khi
Vth
là
sự
biến
đổi
trong
điện
thế
nghỉ
cần
thiết
để
đạt
được
điện
thế
ngưỡng.
Phương
trình
3.56
có
thể
viết
lại
thành
=
trong
phương
trình
3.56
khi
Vth
là
sự
biến
đổi
trong
điện
thế
nghỉ
cần
thiết
để
đạt
được
điện
thế
ngưỡng.
Phương
trình
3.56
có
thể
viết
lại
thành
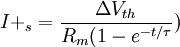 (3.57)
(3.57)
Dòng
điện
nhỏ
nhất
có
thể
được
yêu
cầu
với
điện
thế
màng
để
đạt
dưới
ngưỡng
được
gọi
là
rheobasic
current.
Với
dòng
điện
kích
thích.
khoảng
thời
gian
yêu
cầu
kích
thích
được
xác
định.
Vì
rheobasic
current
là
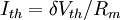 biểu
đồ
thời
gian
có
dạng
biểu
đồ
thời
gian
có
dạng
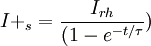 (3.58)
(3.58)
Biểu đồ thời gian được minh họa tong hình 3.13. ở đây, dòng kích thích được chuẩn hóa để dòng dưới ngưỡng có độ bền đơn vị (chú ý rằng, kết quả này đựoc áp dụng cho trạng thái a space-clamp )
Thời gian cần thiết để đạt được điện thế ngưỡng với hai dòng điện kíc thích cơ bản được gọi là chronaxy. với quan hệ giữa chronaxy và hằng số thời gian màng, phương trình 3.57 có thể được viết lại
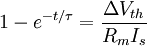 (3.59)
(3.59)
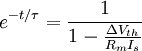 (3.60)
(3.60)
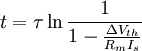 (3.61)
(3.61)
Nếu
dòng
kích
thích
là
hai
dòng
điện
cơ
bản,
khi
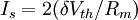 chúng
ta
tính
được
chronaxy
chúng
ta
tính
được
chronaxy
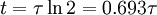 (3.62)
(3.62)
Hình
3.13
(A) Biểu đồ thời gian. Các đơn vị là tương đối
(B) Điện áp chuyển tiếp dưới ngưỡng trước kich thích
Kết
quả
phân
tích
ở
trên
là
gần
đúng
với
một
số
trường
hợp.
Đầu
tiên,
mô
kích
thích
không
thường
được
làm
gần
đúng
với
R
tập
trung
khi
mỗi
yếu
tố
được
phân
phối
theo
một
kiểu
nào
đó.
(Trong
kích
thích
space-clamp,
màng
được
thể
hiện
với
nhiều
kiểu
tập
trung).
Người
ta
cũng
dùng
kiểu
tuyến
tính
là
thỏa
mãn
khoảng
80%
ngưỡng
nhưng
nếu
quá,
màng
cũng
phản
ứng
không
tuyến
tính.
Một
sự
gần
đúng
khác
là
ngưỡng
bất
động,
trong
chương
sau,
chúng
ta
sẽ
mô
tả
sự
thích
ứng,
nó
có
tác
dụng
nâng
cao
ngưỡng
theo
thời
gian
Trong
trạng
thái
đặc
trưng,
biểu
đồ
thời
gian
có
thể
dựa
trên
các
thí
nghiệm.
Trong
trường
hợp
này.
Ngưỡng
cơ
sở
và
chronaxy
được
đo
bằng
thực
nghiệm
của
đáp
ứng
kích
thích.
Kiểu
của
dữ
liệu
với
chronaxy
được
đưa
như
trong
bảng
3.3,
nó
liệt
kê
kiểu
đo
với
dây
thần
kinh
khác
nhau
và
mô
thần
kinh.
Chú
ý
rằng,
thông
thường,
đáp
ứng
được
kỳ
vọng
từ
hệ
thống
sinh
lý
càng
nhanh
thì
giá
trị
chronaxy
càng
nhỏ.
| Mô | Thời gian [ms] | |
| Mô xương | ||
| Ếch (cơ sinh đôi cẳng chân) | 0.2 - 0.3 | |
| Ếch(cơ may) | 0.3 | |
| Rùacơ gấp và cơ duỗi trái | 1 - 2 | |
| Người(cơ gấp cánh tay) | 0.08 - 0.1 | |
| Người (cơ duỗi cánh tay) | 0.16-0.3 | |
| Người (cơ bắp đùi) | 0.10 - 0.7 | |
| Người (cơ mặt)) | 0.24 - 0.7 | |
| Cơ tim | ||
| Ếch (tâm thất) | 3 | |
| Rùa(tâm thất) | 2 | |
| Chó(tâm thất) | 2 | |
| Người(tâm thất) | 2 | |
| Cơ trơn | ||
| Ếch(dạ dày) | 100 | |
| Dây thần kinh | Ếch(hông) | 0.3 |
| Người(phần mô) | 0.2 | |
| Người(tiền đình) | 14 - 22 | |
| Não | ||
| Người(lưỡi) | 1.4 - 1.8 | |
| Người(tế bào quevõng mạc) | 1.2 - 1.8 | |
| Người(tế bào nón võng mạc) | 2.1 - 3.0 |
Tham khảo
Arvanitaki A (1938): Les Variations Graduées De La Polarisation Des Systèmes Excitables, Hermann, Paris.
Bernstein J (1902): Untersuchungen zur Termodynamik der bioelektrischen Ströme. Pflüger Arch. ges. Physiol. 9: 521-62.
Bernstein J (1912): Elektrobiologie, 215 pp. Viewag, Braunschweig.
Davis LJ, Lorente de Nó R (1947): Contributions to the mathematical theory of the electrotonus. Stud. Rockefeller Inst. Med. Res. 131: 442-96.
Eccles JC (1968): The Physiology of Nerve Cells, 270 pp. The Johns Hopkins Press, Baltimore.
Einstein A (1905): Über die von der molekularkinetischen Theorie die wärme Gefordertebewegung von in ruhenden flüssigkeiten suspendierten Teilchen. Ann. Physik 17: 549-60.
Faraday M (1834): Experimental researches on electricity, 7th series. Phil. Trans. R. Soc. (Lond.) 124: 77-122. Fick M (1855): Über Diffusion. Ann. Physik und Chemie 94: 59-86.
Goldman DE (1943): Potential, impedance, and rectification in membranes. J. Gen. Physiol. 27: 37-60.
Hermann L (1905): Beiträge zur Physiologie und Physik des Nerven. Pflüger Arch. ges. Physiol. 109: 95-144.
Hille B (1992): Ionic Channels of Excitable Membranes, 2nd ed., 607 pp. Sinauer Assoc., Sunderland, Mass. (1st ed., 1984)
Hodgkin AL, Huxley AF (1952): A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. (Lond.) 117: 500-44.
Hodgkin AL, Huxley AF, Katz B (1952): Measurement of current-voltage relations in the membrane of the giant axon of Loligo. J. Physiol. (Lond.) 116: 424-48.
Hodgkin AL, Katz B (1949): The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. (Lond.) 108: 37-77.
Hodgkin AL, Rushton WA (1946): The electrical constants of a crustacean nerve fiber. Proc. R. Soc. (Biol.) B133: 444-79.
Katchalsky A, Curran PF (1965): Nonequilibrium Thermodynamics in Biophysics, 248 pp. Harvard University Press, Cambridge, Mass.
Kortum G (1965): Treatise on Electrochemistry, 2nd ed., 637 pp. Elsevier, New York.
Nernst WH (1888): Zur Kinetik der Lösung befindlichen Körper: Theorie der Diffusion. Z. Phys. Chem. 3: 613-37.
Nernst WH (1889): Die elektromotorische Wirksamkeit der Ionen. Z. Phys. Chem. 4: 129-81.
Planck M (1890a): Über die Erregung von Elektricität und Wärme in Elektrolyten. Ann. Physik und Chemie, Neue Folge 39: 161-86.
Planck M (1890b): Über die Potentialdifferenz zwischen zwei verdünnten Lösungen binärer Elektrolyte. Ann. Physik und Chemie, Neue Folge 40: 561-76.
Ruch TC, Patton HD (eds.) (1982): Physiology and Biophysics, 20th ed., 1242 pp. W. B. Saunders, Philadelphia.
Rysselberghe van P (1963): Thermodynamics of Irreversible Processes, 165 pp. Hermann, Paris, and Blaisedell, New York.
Đọc thêm
Edsall JT, Wyman J (1958): Biophysical Chemistry, Vol. 1, 699 pp. Academic Press, New York.
Moore WJ (1972): Physical Chemistry, 4th ed., 977 pp. Prentice-Hall, Englewood Cliffs, N.J.
| trang trước | Hiện tượng màng tế bào | Trang tiếp |