Sách:Điện từ sinh học/Phụ lục A

Giới thiệu

Việc phân tích điện trường và từ trường do tim người phát ra đòi hỏi phải có 1 hệ trục tọa độ nhất quán về mặt toán học và thuận tiện . 1 vài hệ trục tọa độ vuông góc và hệ trục tọa độ cầu đã được sử dụng trong điện tâm đồ nhưng không đáp ứng được hết các yêu cầu đặt ra . Trong điện tâm đồ , hệ trục tọa độ vuông góc bàn tay phải được tiêu chuẩn hóa năm 1967 bởi hiệp hội tim Mĩ ( AHA; American Heart Association, 1967) thường được dùng nhiều nhất . Tuy nhiên , hệ trục tọa độ này là kết quả của sự phát triển mang tính lịch sử và không phải là sự lựa chọn sáng suốt cho các mục đích khác .

Nền tảng của hệ trục tọa độ AHA xuất phát từ các nghiên cứu cơ bản của Willem Einthoven . Einthoven đã định nghĩa trục dương X có hướng từ bên phải sang trái bệnh nhân . Vì vector điện tim ( electric heart vector ) hướng sang bên trái , phía sau và phía dưới , Einhoven đã chọn trục Y hướng xuống dưới , do đó , độ lệch của đỉnh sóng liên hợp QRS là dương . Einhoven đã phát hiện ra tín hiệu ECG chỉ nằm trong mặt phẳng chính diện ( mặt phía trước ) do đó , không cần có trục Z . Khi xây dựng hệ thống biểu đồ vector điện tim , Frank đã chấp nhận hướng của trục X và trục Y mà Einhoven đã định nghĩa , đồng thời ông cũng định nghĩa trục Z hướng về phía sau để có được 1 hệ tọa độ hướng về bên phải ( right-handed coordinate system ) . Hệ tọa độ này cũng được tiêu chuẩn hóa bởi AHA .

Hệ tọa độ của AHA bao gồm các thiếu xót sau đây

1.Liên quan tới mặt phẳng quan sát tự nhiên của bệnh nhân , chỉ có mặt cắt thẳng đứng ( the sagittal plane ) được quan sát từ hướng dương .

2.Hệ tọa độ cầu , lựa chọn hệ tọa độ này với các trục như thường lệ của nó sẽ dẫn đến 1 sự định hướng không quen thộc

Thêm vào đó , nỗ lực của Einhoven nhằm đạt được độ lệch dương của tín hiệu điện theo trục Y lại dẫn đến 1 độ lệch âm của tín hiệu từ . Vì những lí do đó , Malmivuo đã phát triển 1 hệ trục tọa độ nhất quán cho điện tâm đồ nhằm tránh mắc phải những khiếm khuyết ở trên (Malmivuo, 1976; Malmivuo et al., 1977)

Yêu cầu đối với hệ tọa độ vuông góc nhất quán

Hệ tọa độ vuông góc phải đáp ứng được các yêu cầu sau

• 1.Hệ tọa độ vuông góc nên hướng về phía bên phải để nhất quán với quy tắc trong vật lý học và cho phép các ứng dụng không phức tạp sử dụng vào việc phân tích vector và tác động qua lại của lực từ

• 2.Ba mặt phẳng tọa độ là XY , XZ và ZY

• 3.Mỗi mặt phẳng đều được quan sát từ hướng dương

• 4.Các góc trong các mặt phẳng XY , XZ , YZ được đo theo chiều dương ( ngược chiều kim đồng hồ ) từ trục X , trục Y và trục Z .

• 5.Bốn góc phần tư trong mỗi mặt phẳng tọa độ được xác định theo chiều dương , ngược chiều kim đồng hồ và theo thứ tự

I  : 0° tới 90°

II  : 90° tới 180°

III : 180° tới 270°

IV  : 270° tới 360°

Sự liên kết giữa hệ trục tọa độ vuông góc với cơ thể

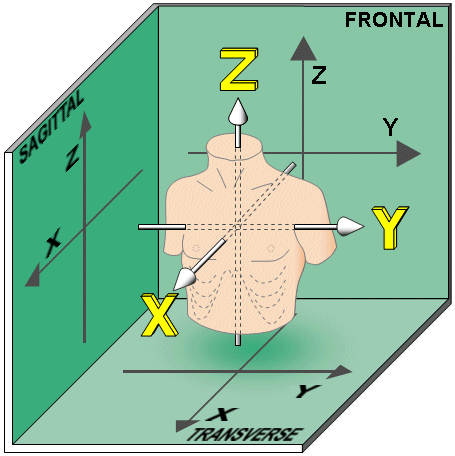
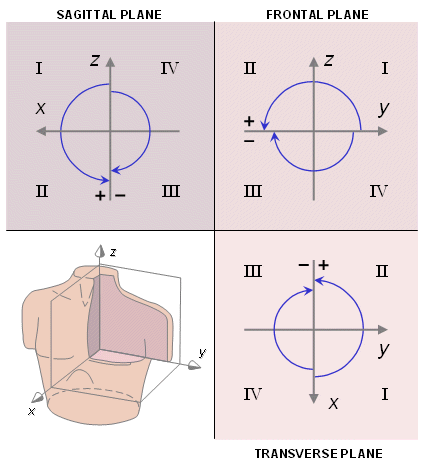
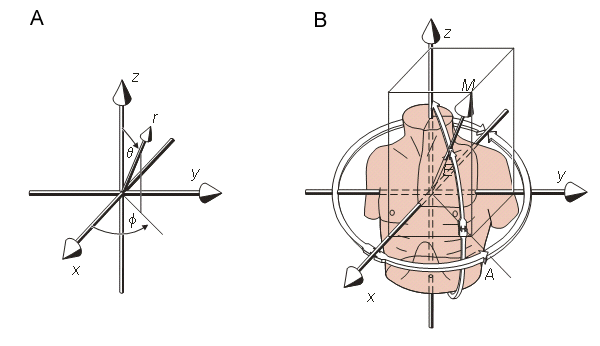
Xuất phát của hệ trục tọa độ vuông góc nên bắt đầu từ phần tâm của tim (the geometric center of the heart ) . Hướng của hệ tọa độ với cơ thể có ít ý nghĩa về mặt toán học nhưng có tầm quan trọng về mặt thực tế lớn . Đó chính là quy tắc kết hợp các trục tọa độ vuông góc với các trục của cơ thể . Có nghĩa là các mặt phẳng tọa độ sẽ tương ứng với mặt phẳng đằng trước , mặt bên trái và mặt nằm ngang . Các mặt phẳng được nhìn từ phía dương và các hướng đó giống với hướng của các vector điện tim nên chiều dương của các trục X , Y , Z được chọn lần lượt là hướng về phía trước , hướng về phía trái và hướng lên trên . Hệ trục tọa độ vuông góc nhất quán được minh họa trong hình A.1 . Ba mặt phẳng tọa độ chứa 4 góc phần tư và quy tắc tính các góc được thể hiện trong hình A.2

Hình A.1. Hệ trục tọa độ vuông góc nhất quán

Hình A.2 . Các mặt phẳng tọa độ của hệ trục tọa vuông góc nhất quán

Hệ tọa độ cầu nhất quán

Có 2 hệ tọa độ cầu ứng với hệ trục tọa độ vuông góc

Hệ tọa độ phân cực cầu nhất quán về mặt toán học ( mathematically consistent spherical polar coordinate system )

Về mặt toán học , hệ tọa độ phân cực cầu được xác định như sau : (A.1 )

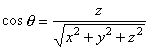
Bán kính vector kí hiệu là r , θ là góc phân cực . Hệ tọa độ này được mô tả như trong hình A.3A

Hệ tọa độ cầu minh họa ( Illustrative Spherical coordinate system )

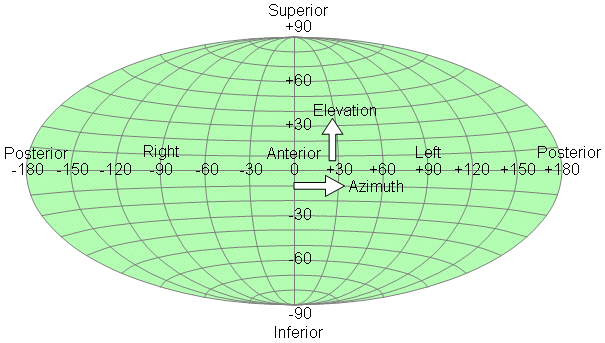
Nếu hoạt động của vector điện tim hay vector từ tim được minh họa trong hệ tọa độ phân cực cầu nhất quán thì chiều tăng của các giá trị sẽ hướng xuống phía dưới của hệ trục . Do đó , để khắc phục điều này , ta sử dụng 1 hệ trục tọa độ cầu quen thuộc hơn trong hình chiếu địa lí của Quả Đất . Hệ trục tọa độ này khác với hệ tọa độ phân cực cầu nhất quán ở trên , không sử dụng θ và φ . Trong hệ trục này , tọa độ cầu quan hệ với tọa độ vuông góc theo các công thức sau :

(A.2)

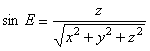
Trong hệ tọa độ cầu minh họa ( Illustrative Spherical coordinate system ) , biên độ của vector kí hiệu là M . Hệ tọa độ này được minh họa như trong hình A.3B . Kĩ thuật hình chiếu sử dụng trong địa lí có thể áp dụng cho các bản đồ từ trường và điện thế trên toàn bộ bề mặt thân cơ thể , như minh họa trong hình A.4

Hình A.3 . Mối quan hệ giữa hệ tọa độ vuông góc và hệ tọa độ cầu A.Hệ tọa độ phân cực cầu nhất quán về mặt toán học B.Hệ tọa độ cầu minh họa Hình A.4. Minh họa bề mặt thân cơ thể trên hệ tọa độ cầu minh họa

So sánh hệ tọa độ nhất quán và hệ tọa độ AHA

Hệ tọa độ nhất quán khác với hệ tọa độ AHA . Các trục tọa độ tương ứng được biểu diễn trong bảng A.1

Hệ tọa độ nhất quán	Hệ tọa độ AHA
X	-Z
Y	+X
Z	-Y
E	-V
A	H + 90°
N	M

X và Z trong hệ tọa độ vuông góc nhất quán có chiều ngược với trong hệ tọa độ AHA . Tuy nhiên , 2 hệ trục tọa độ này biểu diễn vòng vector (vector loop ) giống hệt nhau . So sánh giữa hệ trục tọa độ AHA và hệ trục tọa độ cầu nhất quán thì ta thấy : E và V là giống nhau trong cả 2 hệ trục , dù hướng khác nhau . A và H có hướng giống nhau trong cả 2 hệ .Tuy nhiên , trục tham chiếu trong hệ tọa độ nhất quán khác đi 90° so với hệ trục AHA . Biên độ vector M là giống nhau ở cả 2 hệ trục .

Tọa độ ABC vuông góc

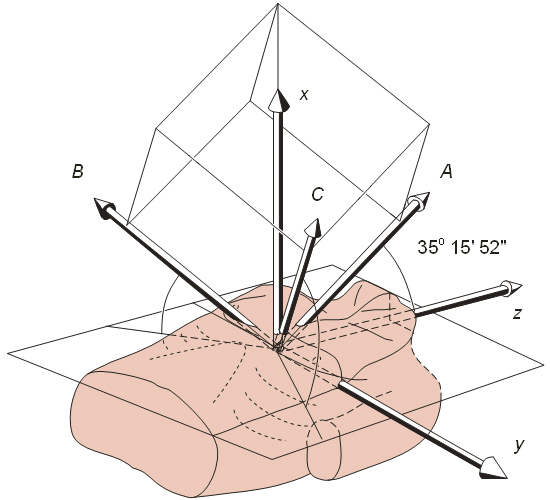
Cùng với hệ trục tọa độ XYZ , hệ trục tọa độ hướng về bên phải (right-handed coordinate system ) cần có tính đối xứng hơn nữa trong mối quan hệ với mặt phẳng phía trước . Ba trục của hệ tọa độ này được chọn làm 3 cạnh của khối hình lập phương có đường chéo song song với trục X . Hệ này được gọi là hệ trục tọa độ ABC . Hình A.5 chỉ ra hướng của các trục trong hệ này so với các trục X , Y , Z . Các trục ABC tạo thành 1 góc 35° 15' 52" so với mặt phẳng YZ . Và góc giữa hình chiếu của nó so với mặt phẳng này là 120° . Hình chiếu của trục A song song với trục Z Các thành phần của 1 vector trong hệ trục ABC có thể chuyển sang hệ trục XYZ với công thức sau:

(A.3)

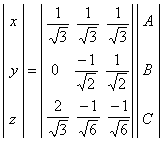
Các thành phần của 1 vector trong hệ trục XYZ có thể chuyển sang hệ trục ABC với công thức sau:

(A.4)

Hình A.5 . Mối quan hệ trực tiếp giữa tọa độ ABC và tọa độ XYZ

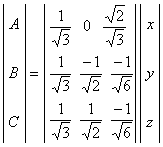
TÀI LIỆU THAM KHẢO

American Heart Association (1967): Recommendations for standardization of leads and of specifications for instruments in electrocardiography and vectorcardiography. Circulation 35: 583-7. (Report of Committee on Electrocardiography).

Frank E (1956): An accurate, clinically practical system for spatial vectorcardiography. Circulation 13:(5) 737-49.

Malmivuo JA (1976): On the detection of the magnetic heart vector - An application of the reciprocity theorem. Helsinki Univ. Tech., Acta Polytechn. Scand., El. Eng. Series. Vol. 39., pp. 112. (Dr. Tech. thesis)

Malmivuo JA, Wikswo JP, Barry WH, Harrison DC, Fairbank WM (1977): Consistent system of rectangular and spherical coordinates for electrocardiography and magnetocardiography. Med. & Biol. Eng. & Comput. 15:(4) 413-5.

Morse PM, Feshbach H (1953): Methods of Theoretical Physics. Part I, 997 pp. McGraw-Hill, New York.

Smythe WR (1968): Static and Dynamic Electricity, 3rd ed., 623 pp. McGraw-Hill, New York.

---

Trang trước

Phụ lục A

Trang tiếp

Liên kết đến đây

• Sách:Điện từ sinh học
• Sách:Điện từ sinh học/Nguồn gốc tín hiệu điện trong mắt
• Sách:Điện từ sinh học/Phụ lục B