Sách:Điện từ sinh học/Phụ lục B
Phụ lục B Ứng dụng của những phương trình trong điện từ sinh học củaof Maxwell
Mục lục
- 1 B.1 Giới thiệu
- 2 B.2 Những phương trình của Maxwell dưới điều kiên không gian tự do
- 3 B.3 Phương trình Maxwell cho phương tiện dẫn hữu hạn
- 4 B.4 Sự đơn giản của những phương trình của Maxwell trong những chế phẩm sinh lý
- 5 B.5 Thế vector từ và điện vô hướng trong phan\mj vi ngoài nguồn
- 6 B.6Kích thích với điện trường và từ trường
- 7 B.7 Những phương trình rút gọn của Maxwell trong chế phẩm sinh lý ở phạm vi ngoài nguồn
- 8 tham khảo
B.1 Giới thiệu
Hành vi của thời gian thay đổi và điện trường và từ trường tĩnh được điều khiển bởi những phương trình của Maxwell được lập bởi James Clerk Maxwell (1865; 1873). Những phương trình tóm tắt một cách đơn giản những kết quả toán học của những thực nghiệm cổ điển của Faraday, Ampere, Coulomb, Maxwell, và những người khác.
Phương trình Maxwell có thể được tìm ra trong những tài liệu cơ bản về lý thuyết điện từ. Tuy nhiên, chúng có thể ứng dụng được một cách cơ bản vào trường điện từ trong không gian tự do (ví dụ.,trường bức xạ). Nơi mà độ dẫn và/ hoặc phương tiện mang tính từ được bao gồm, sau đó, mặc dù những phương trình trở tiếp tục có hiệu lực, nguồn dòng có thể sinh ra trong nhiều cách khác hơn là được xác lập dưới điều kiện không gian tự do. Những sự thay đổi này phải được giới thiệu thông qua một mối quan tâm của bản chất riêng biệt của nguồn dòng phù hợp với những vấn đề tại tay.
Mục đích của chúng tôi ở dây, sau khi giới thiệu về những phương trình của Maxwell trong các hình thức hợp lệ với môi trường không gian tự do, là để đặc trưng hóa chúng để chúng mô tả một cách chính xác điều kiện mà dinh ra trong điện từ sinh học. Sau đó, mục đích của chúng tôi là để đơn giản các phương trình chỗ nào có thể, dựa trên mối liên quan sinh lý điện thực tế.
B.2 Những phương trình của Maxwell dưới điều kiên không gian tự do
Điều kiện đầu
Nguồn
và
Trường:
thời
gian
thay
đổi
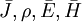
Bộ
dẫn
khối:
hữu
hạn,
không
gian
tự
do
đồng
nhất
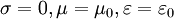
Những phương trình của Maxwell thường xuyên được viết với những dạng vi phân (và vector) cho điều kiện không gian tự do như sau, vì đơn giản cho một biến thể thời gian được giả sử:
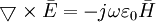 (B.1)
(B.1)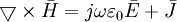 (B.2)
(B.2)
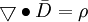 (B.3)
(B.3)
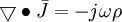 (B.4)
(B.4)
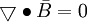 (B.5)
(B.5)
Phương
trình
B.1
là
dạng
của
định
luật
Faraday
một
từ
trường
biến
đổi
theo
thời
gian
 gây
ra
một
điện
trường
gây
ra
một
điện
trường
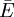 .
.
Phương
trình
B.2
là
dạng
của
định
luật
Ampere,
tích
phân
đường
của
từ
trường
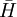 xung
quanh
một
vòng
khép
kín
bằng
tổng
dòng
đi
qua
vòng
đó.
Dòng
điện
được
miêu
tả
như
một
dòng
chuyển
dời
xung
quanh
một
vòng
khép
kín
bằng
tổng
dòng
đi
qua
vòng
đó.
Dòng
điện
được
miêu
tả
như
một
dòng
chuyển
dời
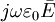 cộng
với
dòng
nguồn
cộng
với
dòng
nguồn
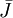 sinh
ra
từ
hoạt
động
đối
lưu
của
điện
tích
trong
chân
không.
sinh
ra
từ
hoạt
động
đối
lưu
của
điện
tích
trong
chân
không.
Phương
trình
B.3
sinh
ra
từ
định
luật
Coulomb
và
liên
quan
tới
sự
chuyển
dời
điện
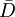 đến
nguồn
nơi
tạo
ra
nó,
cụ
thể
là
mật
độ
điện
tích
đến
nguồn
nơi
tạo
ra
nó,
cụ
thể
là
mật
độ
điện
tích
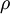 .
.
Phương
trình
B.4
là
dạng
của
định
luật
bảo
toàn
điện
tích,
cụ
thể
là
dòng
ra
của
nó
từ
bất
kì
phạm
vi
gần
nào
(được
tính
từ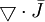 )
có
chỉ
thể
sinh
ra
nếu
vật
chức
điện
tích
bị
mất
hết.
)
có
chỉ
thể
sinh
ra
nếu
vật
chức
điện
tích
bị
mất
hết.
Phương
trình
B.5
nhận
ra
rằng
không
có
điện
tích
từ
nào
tồn
tại,
và
vì
thế
cảm
ứng
từ
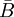 ,
phải
là
solenoidal.
,
phải
là
solenoidal.
B.3 Phương trình Maxwell cho phương tiện dẫn hữu hạn
Điều kiện đầu:
Nguồn
và
Trường:
efm
tĩnh
hoặc
bán
tĩnh,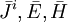 .
.
Bộ
dẫn
khối:
hữu
hạn,
không
đồng
nhất
s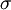 =
=
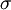 (x,y,z),
(x,y,z),
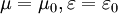 .
.
Quan
tâm
của
chúng
tôi
nằm
trong
điện
trường
và
từ
trường
bên
trong
và
bên
ngoài
các
chế
phẩm
sinh
lý
điện.
Đó
là
những
vùng
bị
cô
lập
(nằm
trong
không
khí)
cái
mà
bao
gồm
mô
dễ
bị
kích
thích
được
bao
quanh
bởi
môi
trường
dẫn
(bộ
dẫn
khối).
Độ
dẫn
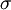 của
bộ
dẫn
khối
,
nói
chung,
là
một
hàm
của
vị
trí
[
của
bộ
dẫn
khối
,
nói
chung,
là
một
hàm
của
vị
trí
[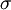 (x,y,z)];
đó
là,
nó
được
giả
sử
là
không
đồng
nhất.
permeq/eability
từ
của
nó
(x,y,z)];
đó
là,
nó
được
giả
sử
là
không
đồng
nhất.
permeq/eability
từ
của
nó
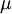 được
giả
sử
một
cách
bình
thường
là
của
không
gian
tự
do
(
được
giả
sử
một
cách
bình
thường
là
của
không
gian
tự
do
(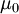 ),
và,
ngoại
trừ
một
vùng
màng
tế
bào
hằng
số
điện
môi
cũng
có
giá
trị
không
gian
tự
do
(
),
và,
ngoại
trừ
một
vùng
màng
tế
bào
hằng
số
điện
môi
cũng
có
giá
trị
không
gian
tự
do
(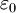 ).
).
Nếu
chúng
ta
quan
tâm
đến
hiện
tại
một
điều
kiện
tĩnh,
sau
đó
chúng
tôi
thấy
rằng
phương
trình
B.1
yêu
cầu
rằng
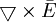
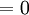 .
Điều
đó
có
nghĩa
là
.
Điều
đó
có
nghĩa
là
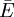 phải
được
bảo
toàn,
một
điều
kiện
nữa
là
phù
hợp
với
điện
trường
sinh
ra
từ
điện
tích
tĩnh
trong
không
gian
tự
do.
Nhưng
trong
phương
tiện
dẫn
của
chúng
tôi,
dòng
chỉ
có
thể
chảy
nếu
có
nguồn
không
bảo
toàn
hiện
tại.
Vì
vậy
chúng
tôi
phải
giả
sử
sự
tồn
tại
của
lực
điện
dịch
emf.
Vì
vậy
với
phương
tiện
dẫn,
phương
trình
B.1
phải
được
sử
đổi
để
có
dạng
B.6,
phải
được
bảo
toàn,
một
điều
kiện
nữa
là
phù
hợp
với
điện
trường
sinh
ra
từ
điện
tích
tĩnh
trong
không
gian
tự
do.
Nhưng
trong
phương
tiện
dẫn
của
chúng
tôi,
dòng
chỉ
có
thể
chảy
nếu
có
nguồn
không
bảo
toàn
hiện
tại.
Vì
vậy
chúng
tôi
phải
giả
sử
sự
tồn
tại
của
lực
điện
dịch
emf.
Vì
vậy
với
phương
tiện
dẫn,
phương
trình
B.1
phải
được
sử
đổi
để
có
dạng
B.6,
Với
lý
do
như
vậy,
chúng
tôi
cũng
phải
nhận
thấy
sự
có
mặt
của
những
trường
dòng
được
đưa
vào
(được
cấp),
cái
mà
chúng
tôi
đặt
là
 ;
những
điều
này
phải
được
bao
gồm
trong
vế
phải
của
phương
trình
B.7,
phù
hợp
với
biểu
thức
B.2
khi
được
cấp
cho
phương
tiện
dẫn.
Nhiều
nguồn
có
thể
được
cố
định
thời
gian
một
cách
cơ
bản
như
với
pin
điện
hóa,
pin
mà
cung
cấp
dòng
điện
sẵn
sàng
cho
bộ
dẫn
khối.
Chúng
cũng
có
thể
là
bán
cố
định,
như
được
ví
dụ
bởi
các
mô
hoạt
động
(dễ
bị
kích
thích);
trong
trường
hợp
này,
nguồn
dòng
không
bảo
toàn
thời
gian
thay
đôi
dẫn
tới
cái
mà,
chuyển,
dòng
chạy
thông
qua
bộ
dẫn
khối
vòng
quanh.
;
những
điều
này
phải
được
bao
gồm
trong
vế
phải
của
phương
trình
B.7,
phù
hợp
với
biểu
thức
B.2
khi
được
cấp
cho
phương
tiện
dẫn.
Nhiều
nguồn
có
thể
được
cố
định
thời
gian
một
cách
cơ
bản
như
với
pin
điện
hóa,
pin
mà
cung
cấp
dòng
điện
sẵn
sàng
cho
bộ
dẫn
khối.
Chúng
cũng
có
thể
là
bán
cố
định,
như
được
ví
dụ
bởi
các
mô
hoạt
động
(dễ
bị
kích
thích);
trong
trường
hợp
này,
nguồn
dòng
không
bảo
toàn
thời
gian
thay
đôi
dẫn
tới
cái
mà,
chuyển,
dòng
chạy
thông
qua
bộ
dẫn
khối
vòng
quanh.
Trong
một
môi
trường
dẫn
nó
không
thể
là
dòng
đối
lưu
như
được
thấy
qua
tham
số
 trong
phương
trình
B.2,
và
vì
thế
nó
bị
bỏ
qua
từ
biểu
thức
B.7.
Dòng
đối
lưu
có
nghĩa
là
để
mô
tả
dòng
chảy
của
điện
tích
trong
chân
không
như
hoạt
động
trong
ống
khuếch
đại
năng
lượng
cao.
(với
lý
do
giống
nhau
đó,
biểu
thức
B.4
là
không
có
hiệu
lực
trong
phương
tiện
dẫn).
Trong
mối
quan
tâm
về
từ
trường
được
cung
cấp,
một
trong
số
đó
có
thể
xử
lý
dòng
được
cung
cấp
chảy
trong
một
cuộn
dây
vật
lý
bằng
cách
lý
tưởng
hóa
nó
như
một
dòng
không
gian
tự
do,
và
vì
thế
giải
thích
cho
nó
với
trong
phương
trình
B.2,
và
vì
thế
nó
bị
bỏ
qua
từ
biểu
thức
B.7.
Dòng
đối
lưu
có
nghĩa
là
để
mô
tả
dòng
chảy
của
điện
tích
trong
chân
không
như
hoạt
động
trong
ống
khuếch
đại
năng
lượng
cao.
(với
lý
do
giống
nhau
đó,
biểu
thức
B.4
là
không
có
hiệu
lực
trong
phương
tiện
dẫn).
Trong
mối
quan
tâm
về
từ
trường
được
cung
cấp,
một
trong
số
đó
có
thể
xử
lý
dòng
được
cung
cấp
chảy
trong
một
cuộn
dây
vật
lý
bằng
cách
lý
tưởng
hóa
nó
như
một
dòng
không
gian
tự
do,
và
vì
thế
giải
thích
cho
nó
với ở
vế
phải
của
phương
trình
B.2.
Vì
dòng
này
là
sonenoit
cơ
bản,
nó
không
được
kết
hợp
với
mật
độ
điện
tích.
Trong
công
thức
này
ý
nghĩa
của
ở
vế
phải
của
phương
trình
B.2.
Vì
dòng
này
là
sonenoit
cơ
bản,
nó
không
được
kết
hợp
với
mật
độ
điện
tích.
Trong
công
thức
này
ý
nghĩa
của cần
thiết
được
thiết
lập
không
được
xem
xét
một
cách
rõ
ràng.
cần
thiết
được
thiết
lập
không
được
xem
xét
một
cách
rõ
ràng.
Bởi
vì
độ
dẫn
điện
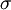 của
bộ
dẫn
khối
chúng
tôi
cần
đưa
vào
vế
phải
của
phương
trình
B.7
dòng
dẫn
của
bộ
dẫn
khối
chúng
tôi
cần
đưa
vào
vế
phải
của
phương
trình
B.7
dòng
dẫn
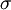 ,
ngoài
sự
tồn
tại
của
dòng
điện
dich
,
ngoài
sự
tồn
tại
của
dòng
điện
dich
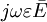 .
.
Một
sự
sửa
đổi
khác
đến
từ
việc
thừa
nhận
rằng
một
mật
độ
điện
tích
khối
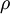 không
thể
tồn
tại
cùng
với
một
phương
tiện
dẫn
(qua
những
điện
tích
mặt
có
thể
tích
lũy
tại
giao
diện
giữa
những
vùng
có
độ
dẫn
khác
nhau-nhất
là
tương
đương
với
điện
tích
mà
nằm
trên
tấm
kim
loại
của
tụ.)
Vì
thế,
phương
trình
B.3
không
được
cung
cấp
trong
phương
tiện
dẫn.
không
thể
tồn
tại
cùng
với
một
phương
tiện
dẫn
(qua
những
điện
tích
mặt
có
thể
tích
lũy
tại
giao
diện
giữa
những
vùng
có
độ
dẫn
khác
nhau-nhất
là
tương
đương
với
điện
tích
mà
nằm
trên
tấm
kim
loại
của
tụ.)
Vì
thế,
phương
trình
B.3
không
được
cung
cấp
trong
phương
tiện
dẫn.
Với những vấn đề được quan tâm đó, nhưng phương trình của Maxwell bây giờ có thể được viết lại cho phương tiện dẫn hữu hạn như sau:
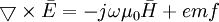 (B.6)
(B.6)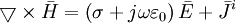 (B.7)
(B.7)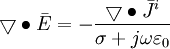 (B.8)
(B.8)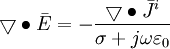 (B.9)
(B.9)
Trong
tập
hợp
các
phương
trình
trên,
chúng
tôi
thu
được
phương
trình
B.8
bằng
cách
phân
kì
cả
hai
vế
của
B.7
và
chú
ý
rắngự
phân
kì
của
dòng
xoáy
của
bất
kỳ
hàm
vector
nào
đều
có
đặc
điểm
là
bằng
zero
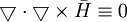 .
.
B.4 Sự đơn giản của những phương trình của Maxwell trong những chế phẩm sinh lý
Điều kiện đâu:
Nguồn
và
Trường:
bán
tĩnh
(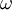 <
1000
Hz)
<
1000
Hz)
 Bộ
dẫn
nguồn:
hữu
hạn
giới
hạn
(r
<1m)
điện
trở
không
đồng
nhất
Bộ
dẫn
nguồn:
hữu
hạn
giới
hạn
(r
<1m)
điện
trở
không
đồng
nhất
Những
chế
phẩm
sinh
lý
của
mối
quan
tâm
về
sinh
lý
điện
có
một
vài
đặc
điểm
trên
đó
mà
có
thể
được
dựa
trên
sự
đơn
giản
chắc
chắn
của
những
phương
trình
cơ
bản
của
Maxwell.
Chúng
tôi
đã
từng
đề
cập
đến
rằng
chúng
tôi
hi
vọng
hằng
số
điện
môi
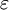 và
độ
từ
thẩm
và
độ
từ
thẩm
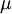 trong
bộ
dẫn
khối
có
giá
trị
của
không
gian
tự
do
trong
bộ
dẫn
khối
có
giá
trị
của
không
gian
tự
do
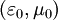 .
Ba
điều
kiện
khác
sẽ
được
giới
thiệu
ở
đây.
.
Ba
điều
kiện
khác
sẽ
được
giới
thiệu
ở
đây.
B.4.1 Giới hạn tần số
Mật độ phổ năng lượng của tín hiệu của nguồn gốc sinh học đã từng được đo. Nó đã từng được tìm thấy thay đổi phụ thuộc vào bản chất của nguồn ( ví dụ, thần kinh, cơ…). Những tần số cao nhất được thấy ở trong điện tâm đồ. Ở đây băng thông cho thiết bị lâm sàng thường nằm dưới 100 Hz, mặc dù nhiều chất lượng tốt nhất yêu cầu yêu cầu tần số trên 200-500 Hz. Trong nghiên cứu nó thường được giả sử là dưới 1000Hz, và chúng tôi sẽ xem xét sự bình thường này dưới tần số giới hạn. Barr và Spach (1977) đã từng chỉ ra rằng với tần số thế trong tim cao khoảng 10 kHz có thể cần được đưa vào cho việc tái tạo tín hiệu ban đầu. Khi chúng tôi xem xét rằng xung nhip hoạt động là 1ms, sau đó tín hiệu nhờ vào nguồn phải có năng lượng nhỏ trên 1kHz. Liên quan tới phổ tần số hoàn toàn mà Maxwell đã từng đề cập, nó chắc chắn là một phạm vi tần số thấp. Sự đơn giản kết quả được mô tả ở phần tiếp theo.
B.4.2 Giới hạn kích thước
Hi vọng trong nhiều trường hợp đặc biệt nơi mà chúng tôi đang nghiên cứu, nói rằng , ECG của cá voi , kích thước của bộ dẫn khối có thể được trông đợi nằm bán kính cầu khoảng 1m. Như một hình cầu sẽ phù hợp với hầu hết mọi cơ thể người nguyên vẹn, và chắc chắn điển hình trong chế phẩm trong ống nghiệm được nghiên cứu trong phòng nghiên cứu. Vì thế, được bàn ở phần tiếp theo , là thế trễ của mối quan tâm cơ bản không sinh ra.
B.4.3 Trở kháng bộ dẫn khối
Bộ
dẫn
khối
thường
chứa
vài
yếu
tố
rời
rạc
như
tế
bào
thần
kinhm
cơ,
mô
liên
kết,
mô
mạch,
da
và
chất
hữu
cơ
khác.
Với
nhiều
trường
hợp,
tính
dẫn
có
thể
được
mô
tả
bởi
độ
dẫn
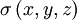 thu
được
từ
việc
trung
hòa
qua
một
vùng
nhỏ
nhưng
đa
bào.
Vì
như
một
vùng
vĩ
mô
chứa
màng
tế
bào
lipid
hằng
số
điện
môi
có
thể
được
chia
từ
giá
trị
không
gian
tự
do.
Cả
hai
giá
trị
thu
được
từ
việc
trung
hòa
qua
một
vùng
nhỏ
nhưng
đa
bào.
Vì
như
một
vùng
vĩ
mô
chứa
màng
tế
bào
lipid
hằng
số
điện
môi
có
thể
được
chia
từ
giá
trị
không
gian
tự
do.
Cả
hai
giá
trị
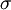 và
và
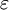 đưa
vào
phương
trình
B.7
và
B.8
sẽ
phụ
thuộc
vào
đặc
điểm
mô
đặc
trưng
và
tần
số.
Bằng
cách
tạo
ra
phép
đo
vĩ
mô,
Schwan
và
Kay
(1957)
đã
xác
định
rằng
đưa
vào
phương
trình
B.7
và
B.8
sẽ
phụ
thuộc
vào
đặc
điểm
mô
đặc
trưng
và
tần
số.
Bằng
cách
tạo
ra
phép
đo
vĩ
mô,
Schwan
và
Kay
(1957)
đã
xác
định
rằng
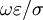 cho
khoảng
tần
số
10
Hz
<
f
<
1000
Hz
là
dưới
0.15.
Nhưng
trong
nhiều
trường
hợp
có
thể
điều
trị
tất
cả
các
màng
tế
bào
một
cách
đặc
biệt.
Trong
trường
hợp
này
nó
là
không
gian
còn
lại
kẽ
nội
bào
và
thành
phần
tạo
nên
bộ
dẫn
khối,
và,
vì
lipid
không
có,
các
phương
tiện
sẽ
hoạt
động
trở
kháng
qua
toàn
bộ
phổ
tần
số
quan
tâm.
Trong
trường
hợp
khác,
nó
có
thể
làm
tăng
để
tránh
dòng
điện
dịch
cùng
với
bộ
dẫn
khối
trong
phương
trình
B.7
và
B.8
.
(Tất
nhiên,
người
ta
phải
luôn
luôn
đưa
vào
dòng
màng
tụ
khi
bộ
phận
quan
tâm
của
dòng
màng
tổng).
Vì
thế,
những
phương
trình
này
có
thể
được
rút
gọn
cho
phương
trình
B.10
và
B.11,
tương
ứng:
cho
khoảng
tần
số
10
Hz
<
f
<
1000
Hz
là
dưới
0.15.
Nhưng
trong
nhiều
trường
hợp
có
thể
điều
trị
tất
cả
các
màng
tế
bào
một
cách
đặc
biệt.
Trong
trường
hợp
này
nó
là
không
gian
còn
lại
kẽ
nội
bào
và
thành
phần
tạo
nên
bộ
dẫn
khối,
và,
vì
lipid
không
có,
các
phương
tiện
sẽ
hoạt
động
trở
kháng
qua
toàn
bộ
phổ
tần
số
quan
tâm.
Trong
trường
hợp
khác,
nó
có
thể
làm
tăng
để
tránh
dòng
điện
dịch
cùng
với
bộ
dẫn
khối
trong
phương
trình
B.7
và
B.8
.
(Tất
nhiên,
người
ta
phải
luôn
luôn
đưa
vào
dòng
màng
tụ
khi
bộ
phận
quan
tâm
của
dòng
màng
tổng).
Vì
thế,
những
phương
trình
này
có
thể
được
rút
gọn
cho
phương
trình
B.10
và
B.11,
tương
ứng:
Những phương trình của Maxwell cho những ứng dụng sinh lý có dạng:
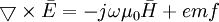 (B.6)
(B.6)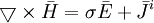 (B.10)
(B.10)
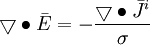 (B.11)
(B.11)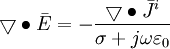 (B.9)
(B.9)B.5 Thế vector từ và điện vô hướng trong phan\mj vi ngoài nguồn
Điều kiện đầu:
Nguồn:
bán
tĩnh
 (
( <
1000
Hz)
<
1000
Hz)
Bộ
dẫn
khối:
hữu
hạn
giới
hạn
(r
<
1m)
ngoài
vùng
nguồn
trở
kháng
không
đồng
nhất
(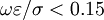 ),
),
Trong
phần
này,
chúng
tôi
dẫn
từ
những
phương
trình
của
Maxwell
những
phương
trình
cho
thế
vector
từ
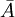 và
thế
điện
vô
hướng
và
thế
điện
vô
hướng
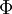 trong
những
ứng
dụng
sinh
lý.,
phương
trình
B.19
và
B.21
tương
ứng
trong
những
ứng
dụng
sinh
lý.,
phương
trình
B.19
và
B.21
tương
ứng
Vì
sự
phân
kì
của
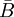 bằng
zero
(phương
trình
b.9),
từ
trường
có
thể
được
dẫn
từ
dòng
xoáy
của
trường
vector
tự
do
bằng
zero
(phương
trình
b.9),
từ
trường
có
thể
được
dẫn
từ
dòng
xoáy
của
trường
vector
tự
do
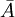 ,
được
gọi
là
thế
vector
từ.
Điều
này
đáp
ứng
những
yêu
cầu
được
chỉ
ra
trong
phương
trình
B.9
bởi
vì
sự
phân
kì
của
dòng
xoáy
của
bất
kì
trường
vector
nào
đều
bằng
zero
một
cách
cần
thiết,
vì
thế,
,
được
gọi
là
thế
vector
từ.
Điều
này
đáp
ứng
những
yêu
cầu
được
chỉ
ra
trong
phương
trình
B.9
bởi
vì
sự
phân
kì
của
dòng
xoáy
của
bất
kì
trường
vector
nào
đều
bằng
zero
một
cách
cần
thiết,
vì
thế,
 (B.12)
(B.12)
Vì
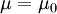 ,
chúng
tôi
có
thể
thế
phương
trình
B.12
vào
B.6.
Chúng
tôi
chỉ
xem
xét
vùng
khối
dẫn
bên
ngoài
màng
tế
bào
nơi
mà
emfs
là
zero
(chú
ý
rằng
emfs
đưa
vào
một
cách
xác
định
cùng
với
màng
tế
bào
trong
dạng
của
pin
thế
Nernst),
và
chúng
tôi
thu
được
,
chúng
tôi
có
thể
thế
phương
trình
B.12
vào
B.6.
Chúng
tôi
chỉ
xem
xét
vùng
khối
dẫn
bên
ngoài
màng
tế
bào
nơi
mà
emfs
là
zero
(chú
ý
rằng
emfs
đưa
vào
một
cách
xác
định
cùng
với
màng
tế
bào
trong
dạng
của
pin
thế
Nernst),
và
chúng
tôi
thu
được
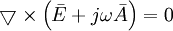 (B.13)
(B.13)
Bây
giờ,
khi
dòng
xoáy
của
trường
vector
là
zero,
trường
vector
đó
có
thể
được
lấy
như
gradient
(âm)
của
một
trường
thế
vô
hướng
xác
định
(
trường
mà
chúng
tôi
đặt
với
kí
hiệu
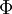 và
chú
thích
là
thế
điện
vô
hướng).
Sự
gán
này
là
cố
định
vì
dòng
xoáy
của
gradient
của
bât
kì
trường
vô
hướng
nào
cùng
bằng
0.
Vì
thế
phương
trình
B.13
được
rút
gọn
như
sau.
và
chú
thích
là
thế
điện
vô
hướng).
Sự
gán
này
là
cố
định
vì
dòng
xoáy
của
gradient
của
bât
kì
trường
vô
hướng
nào
cùng
bằng
0.
Vì
thế
phương
trình
B.13
được
rút
gọn
như
sau.
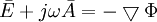 (B.14)
(B.14)
Theo
lý
thuyết
của
Helmholtz,
một
trường
vector
được
đặc
trưng
duy
nhất
bởi
cả
dòng
phân
kì
và
xoáy
của
nó
(Plonsey
và
Collin,
1961).
Vì
chỉ
có
dòng
xoáy
của
trường
vector
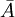 vừa
được
chỉ
ra
ở
trên
(trong
phương
trình
B.12),
bây
giờ
chúng
ta
có
thể
chọn
vừa
được
chỉ
ra
ở
trên
(trong
phương
trình
B.12),
bây
giờ
chúng
ta
có
thể
chọn
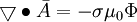 (B.15)
(B.15)
Sự
lựa
trọn
đặc
biệt
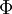 từ
phương
trình
khác
nhau
cho
từ
phương
trình
khác
nhau
cho
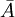 (phương
trình
B.17).
Đó
là,
nó
có
hiệu
ứng
mô
tả
được
của
sự
phân
chia
thế
vector
từ
(phương
trình
B.17).
Đó
là,
nó
có
hiệu
ứng
mô
tả
được
của
sự
phân
chia
thế
vector
từ
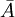 từ
thế
điện
vô
hướng
từ
thế
điện
vô
hướng
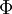 .
Như
một
sự
quan
tâm
được
gợi
ý
ban
đầu
bởi
Lorentz
khi
trao
đổi
với
không
gian
tự
do
của
những
phương
trình
Maxwell.
Lorentz
đã
giới
thiệu
một
phương
trình
tương
tụ
với
phương
trình
B.15
được
biết
đến
như
điều
kiện
Lorentz,
đó
là
.
Như
một
sự
quan
tâm
được
gợi
ý
ban
đầu
bởi
Lorentz
khi
trao
đổi
với
không
gian
tự
do
của
những
phương
trình
Maxwell.
Lorentz
đã
giới
thiệu
một
phương
trình
tương
tụ
với
phương
trình
B.15
được
biết
đến
như
điều
kiện
Lorentz,
đó
là
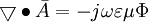 (B.16)
(B.16)
Chúng
tôi
đã
từng
thay
đổi
biểu
thức
này
từ
khi
loại
bỏ
trong
phương
trình
B.10
và
B.11
dòng
điện
dịch
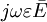 có
lợi
cho
dòng
dẫn
có
lợi
cho
dòng
dẫn
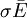 .
Điều
này
đưa
ra
thay
thế
.
Điều
này
đưa
ra
thay
thế
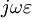 bởi
bởi
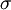 trong
điều
kiện
lorentz
cơ
bản
(phương
trình
B.16),
kết
quả
trong
B.15.
Điều
kiện
lorentz
cũng
có
thể
được
chỉ
ra
để
có
những
tính
quan
trọng
khác,
cụ
thể
là
no
chắc
chắn
yếu
tố
cố
định
của
điều
kiện
tiếp
tục.
trong
điều
kiện
lorentz
cơ
bản
(phương
trình
B.16),
kết
quả
trong
B.15.
Điều
kiện
lorentz
cũng
có
thể
được
chỉ
ra
để
có
những
tính
quan
trọng
khác,
cụ
thể
là
no
chắc
chắn
yếu
tố
cố
định
của
điều
kiện
tiếp
tục.
Bây
giờ,
nếu
chúng
tôi
thế
phương
trình
B.12,
14,
15
vào
B.10,
giữ
nguyên
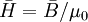 ,
và
nếu
chúng
tôi
sử
dụng
vector
riêng
,
và
nếu
chúng
tôi
sử
dụng
vector
riêng
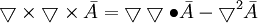 (B.17)
(B.17)Chúng tôi thu được
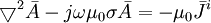 (B.18)
(B.18)
Giống
như
emfs
được
loại
bỏ
bằng
cách
chú
ý
đến
vùng
bên
ngoài
màng
tế
bào
dễ
kích
thích,
vì
vậy
cũng
có
thể
loại
bỏ
dòng
không
đối
lưu
 trong
phương
trình
B.10.
Trong
trường
hợp
này
tất
cả
các
phương
trình
mô
tả
điều
kiện
trong
không
gian
nội
bào
và
ngoại
bào
bị
động;
hiệu
ứng
của
nguồn
cùng
với
màng
tế
bào
sau
đó
đưa
vào
sole
qua
những
điều
kiện
biên
tại
và
qua
màng
tế
bào.
Mặt
khác,
nó
là
hữu
ích
để
giữ
trong
phương
trình
B.10.
Trong
trường
hợp
này
tất
cả
các
phương
trình
mô
tả
điều
kiện
trong
không
gian
nội
bào
và
ngoại
bào
bị
động;
hiệu
ứng
của
nguồn
cùng
với
màng
tế
bào
sau
đó
đưa
vào
sole
qua
những
điều
kiện
biên
tại
và
qua
màng
tế
bào.
Mặt
khác,
nó
là
hữu
ích
để
giữ
 như
một
hàm
nguồn
được
phân
bố
trong
phương
trình
B.10.
Trong
khi
nó
được
giữ
thực
tế
để
màng
tế
bào
đảm
bảo
điều
kiện
biên
đã
được
đề
cập
trước
đây,
nó
có
thể
được
rút
gọn
và
liên
quan
như
một
nguồn
tương
đương
mà
được
phân
chia
một
cách
đồng
nhất
thông
qua
nguồn
khối.
Với
những
điểm
trường
bên
ngoài
phạm
vi
nguồn
mà
ở
khoảng
cách
lớn
hơn
so
với
kích
thước
màng
tế
bào
(qua
kích
thước
trung
bình
như
một
hàm
nguồn
được
phân
bố
trong
phương
trình
B.10.
Trong
khi
nó
được
giữ
thực
tế
để
màng
tế
bào
đảm
bảo
điều
kiện
biên
đã
được
đề
cập
trước
đây,
nó
có
thể
được
rút
gọn
và
liên
quan
như
một
nguồn
tương
đương
mà
được
phân
chia
một
cách
đồng
nhất
thông
qua
nguồn
khối.
Với
những
điểm
trường
bên
ngoài
phạm
vi
nguồn
mà
ở
khoảng
cách
lớn
hơn
so
với
kích
thước
màng
tế
bào
(qua
kích
thước
trung
bình
 hoạt
động)
trường
được
phát
gần
với
giá
trị
chính
xác.
hoạt
động)
trường
được
phát
gần
với
giá
trị
chính
xác.
Phưong
trình
B.18
được
biết
như
phương
trình
Helmholtz
vector,
mà
giải
pháp
trong
dạng
tích
phân
được
biết
trong
điện
từ
cơ
bản
(Plonsey
and
Collin,
1961).
Thích
ứng
như
một
giải
pháp
cho
phương
trình
đặc
biệt
của
chúng
tôi
mang
đến
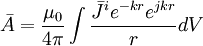 (B.19)
(B.19)ở đây
![k={\sqrt {\omega \mu _{0}\sigma /2}}\left[1/m\right]](https://tusach.thuvienkhoahoc.com/images/math/0/d/8/0d81267a19b1036548333c1461925503.png)
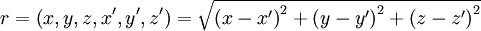
Chú
ý
rằng
r
là
bán
kính
từ
yếu
tố
nguồn
dV(x,y,z)
(hệ
tọa
độ
phụ)
cho
trường
điểm
P(x',y',z')
(hệ
tọa
độ
chính),
và
vì
thế
là
một
hàm
của
cả
hệ
tọa
độ
chính
và
phụ
Để
đánh
giá
độ
lớn
của
krtrong
các
hàm
mũ
trong
phương
trình
B.19
chúng
tôi
chọn:
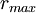 =
100
cm
=
100
cm
 =
2π•1000
1/s
=
2π•1000
1/s
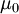 =
4π•10-9
H/cm
=
4π•10-9
H/cm
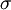 =
.004
S/cm
=
.004
S/cm
sau
đó
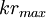 =
.04
vì
=
.04
vì
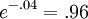 ,số
hạng
mũ
có
thể
được
bỏ
qua
và
chúng
tôi
lấy
một
phương
trình
rút
gọn
B.19,
đưa
vào
thế
vector
từ
dưới
điều
kiện
sinh
lý
điện:
,số
hạng
mũ
có
thể
được
bỏ
qua
và
chúng
tôi
lấy
một
phương
trình
rút
gọn
B.19,
đưa
vào
thế
vector
từ
dưới
điều
kiện
sinh
lý
điện:
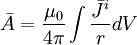 (B.20)
(B.20)
Thế
điện
vô
hướng
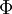 có
thể
được
tìm
thấy
từ
có
thể
được
tìm
thấy
từ
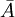 bằng
việc
sử
dụng
phương
trình
B.15
với
phương
trình
B.20.
Cũng
trong
việc
đó,
chúng
tôi
chú
ý
rằng
phương
trình
B.20
bao
gồm
sự
thực
hiện
tại
hệ
tọa
độ
trường
(x',y',z').Ta
có
bằng
việc
sử
dụng
phương
trình
B.15
với
phương
trình
B.20.
Cũng
trong
việc
đó,
chúng
tôi
chú
ý
rằng
phương
trình
B.20
bao
gồm
sự
thực
hiện
tại
hệ
tọa
độ
trường
(x',y',z').Ta
có
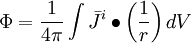 (B.21)
(B.21)
ở
đây
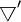 chỉ
hoạt
động
trong
hệ
tọa
độ
trường,
đó
là
tại
sao
chỉ
hoạt
động
trong
hệ
tọa
độ
trường,
đó
là
tại
sao
 không
bị
ảnh
hưởng.
Vì
không
bị
ảnh
hưởng.
Vì
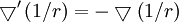 ,
cuối
cùng
chúng
tôi
lấy
cho
thế
điện
vô
hường:
,
cuối
cùng
chúng
tôi
lấy
cho
thế
điện
vô
hường:
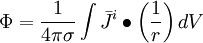 (B.22)
(B.22)
Phương
trình
B.22
được
đặc
trưng
cho
biểu
thức
trường
tĩnh,
ở
đây
 được
biết
như
là
một
hàm
nguồn
mật
độ
lưỡng
cực
khối.
Phương
trình
này
phù
hợp
một
cách
chính
xác
với
phương
trình
7-5.
Mặc
dù
phương
trình
dạng
tĩnh
cung
cấp,
được
biết
như
là
một
hàm
nguồn
mật
độ
lưỡng
cực
khối.
Phương
trình
này
phù
hợp
một
cách
chính
xác
với
phương
trình
7-5.
Mặc
dù
phương
trình
dạng
tĩnh
cung
cấp,
 là
thời
gian
thay
đổi
thực
tế,
và
vì
vậy,
phải
là
thời
gian
thay
đổi
thực
tế,
và
vì
vậy,
phải
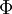 là
thay
đổi
thời
gian
một
cách
đồng
bộ.
Chúng
tôi
gọi
những
trường
hợp
này
là
bán
tĩnh.
là
thay
đổi
thời
gian
một
cách
đồng
bộ.
Chúng
tôi
gọi
những
trường
hợp
này
là
bán
tĩnh.
Khi
nguồn
sinh
ra
dòng
điện
(bao
gồm
cả
kích
thích
tế
bào),
một
từ
trường
cần
thiết
được
tạo
ra
bởi
kết
quả
của
dòng
chảy.
Cuối
cùng
mang
đến
một
thế
vector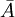 ,
mà
góp
phần
vào
trường
điện
kết
quả
,
mà
góp
phần
vào
trường
điện
kết
quả
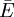 thông
qua
số
hạng
thông
qua
số
hạng
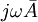 trong
phương
trình
B.14.
Tuy
nhiên,
dưới
điều
kiện
được
chỉ
ra,
trong
phương
trình
B.14.
Tuy
nhiên,
dưới
điều
kiện
được
chỉ
ra,
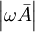 là
không
đáng
kể
khi
so
với
số
hạng
là
không
đáng
kể
khi
so
với
số
hạng
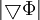 như
được
trình
bày
ở
trong
Plonsey
and
Heppner
(1967).
Đưới
những
điều
kiện
đó
chúng
tôi
chỉ
rời
đi
một
số
hạng
thế
vô
hướng,
và
phương
trình
B.14
được
rút
gọn
thành
như
được
trình
bày
ở
trong
Plonsey
and
Heppner
(1967).
Đưới
những
điều
kiện
đó
chúng
tôi
chỉ
rời
đi
một
số
hạng
thế
vô
hướng,
và
phương
trình
B.14
được
rút
gọn
thành
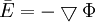 (B.23)
(B.23)
Biểu
thức
này
cũng
phù
hợp
với
công
thức
dạng
tĩnh.
Nó
nên
được
nhớ
rằng
phương
trình
B.23
là
không
chính
xác,
nhưng
chỉ
là
một
xấp
xỉ
tốt.
Nó
phù
hợp
với
điều
kiện
bán
tĩnh
nơi
mà
điện
trường
tương
tự
với
cái
mà
sinh
ra
dưới
điều
kiện
tĩnh.
Dưới
điều
kiện
tĩnh
thực
sự
điện
trường
và
từ
trường
độc
lập
hoàn
toàn.
Dưới
điều
kiện
bán
tĩnh,
trong
khi
những
trường
đáp
ứng
phương
trình
tĩnh
,
sự
thay
đổi
thời
gian
tần
số
thấp
có
thể
được
xếp
chồng
(được
chứng
minh
bởi
điều
kiện
tần
số
thấp
như
đã
nói
ở
trên),
trong
trường
hợp
đó
hiệu
ứng
từ
trường,
mặc
dù
hiện
còn,
có
thể
thường
được
bỏ
qua.
Chú
ý
rằng
trong
trường
hợp
này,
nơi
mà
nguồn
là
điện
sinh
học
riêng
và
dạng
rút
gọn
của
phương
trình
B.23
là
cố
định,
phương
trình
B.11
dẫn
tới
phương
trình
7.2
(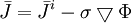 .
.
B.6Kích thích với điện trường và từ trường
B.6.1 Kích thích với điện trường
Điều kiện đâu:
Nguồn: điện trường trạng thái sẵn sàng
Bộ dẫn: sợi đồng nhất trong bộ dẫn khối
Các ý kiến ở trên, chúng tôi cũng quan tâm đến trường hợp nơi mà mô dễ bị kích thích được kích thích một cách riêng biệt với từ trường được cung cấp. Trong trường hợp này thế vector là lớn và có thể được bỏ qua. Thực tế, để bỏ qua những trường hợp này là để bỏ qua các hàm ràng buộc cơ bản , mà sẽ để lại kết quả vô lý không của trường nào , hoặc điện hoặc từ.
Chúng tôi đã từng chỉ ra trong chương 3 mà với một dây dẫn đơn đồng nhất dưới điều kiên trạng thái sẵn sằng một phần đông nhất phương trinh tich phân (phương trình 3.46) sinh ra:
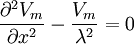 (b.24)
(b.24)ở đây:
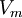 :
là
tế
màng
vận
chuyển
:
là
tế
màng
vận
chuyển
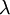 :
không
gian
cố
định,
đặc
điểm
của
tính
điện
và
từ
của
dây
:
không
gian
cố
định,
đặc
điểm
của
tính
điện
và
từ
của
dây
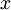 :
hệ
tọa
độ
theo
hướng
của
dây
:
hệ
tọa
độ
theo
hướng
của
dây
Với một nguồn điểm tại gốc chúng tôi cung đã từng chỉ ra một cách cụ thể, trong chương 3, ở đó giải pháp cho phương trình B.24 là (phương trình 3.49)
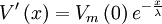 (B.25)
(B.25)
ở
đây
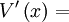 độ
lệch
của
điện
thế
màng
với
điện
thế
nghỉ
độ
lệch
của
điện
thế
màng
với
điện
thế
nghỉ
Trong phương trình
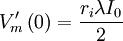 (B.26)
(B.26)ở đây:
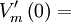 thế
màng
vận
chuyển
tại
gốc
thế
màng
vận
chuyển
tại
gốc
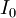 =
dòng
điểm
nội
bào
được
cung
cấp
=
dòng
điểm
nội
bào
được
cung
cấp
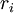 =
trở
kháng
trục
nội
bào
trên
mỗi
đơn
vị
chiều
dài
=
trở
kháng
trục
nội
bào
trên
mỗi
đơn
vị
chiều
dài
Chúng
tôi
thấy
ở
đây,
rằng
với
hơn
một
trường
thế
vô
hướng
được
cung
cấp,
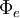 ,
phương
trình
B.24
trở
thành
,
phương
trình
B.24
trở
thành
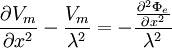 (B.27)
(B.27)
Có
thể
nhận
ra
trong
phương
trình
này
là
đạo
hàm
thứ
hai
của
trường
thế
được
cung
cấp
dọc
theo
dây
là
hàm
bắt
buộc
(thực
tế,
nó
đã
từng
được
gọi
là
hàm
chức
năng,
trong
khi
các
biến
phụ
thuộc,
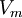 ,
là
đáp
ứng
của
màng
với
kích
thích.
Sử
dụng
phương
trình
B.23,
chúng
tôi
có
thể
viết
phương
trình
B.24
như
,
là
đáp
ứng
của
màng
với
kích
thích.
Sử
dụng
phương
trình
B.23,
chúng
tôi
có
thể
viết
phương
trình
B.24
như
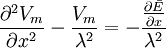 (B.28)
(B.28)
ở
đây
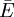 là
điện
trường
được
cung
cấp
là
điện
trường
được
cung
cấp
B.6.2 Kích thích với từ trường
Điều kiện đầu:
Nguồn: Từ trường thời gian thay đỏi
Bộ dẫn khối: cáp đồng nhất trong bộ dẫn khối
Kích
thích
điện
có
thể
được
tạo
ra
bởi
việc
cung
cấp
từ
trường
thời
gian
thay
đổi
vào
mô.
Như
được
đưa
ra
trong
phương
trình
B.12,
từ
trường
được
định
nghĩa
như
một
dòng
xoáy
của
thế
vector.
Bây
giờ
sự
kích
thích
được
giới
thiệu
riêng
rẽ
thông
qua
một
từ
trường
gây
ra
một
điện
trường.
Phương
trình
B.27
vẫn
hợp
lệ
ngoại
trừ
trường
được
cung
cấp
được
tìm
thấy
trong
phương
trình
B.14,
cụ
thể
là
ở
đây
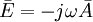 .
.
Việc xác định trường vector từ một cuộn dây vật lý được tìm thấy, một cách cơ bản, từ phương trình B.20 (phương trình phù hợp với phương trình 12.33). Mối quan hệ này cũng đã từng được làm ra và phổ biến cho nhiều cấu hình cuộn dây khác nhau.
Chúng
tôi
cũng
chú
ý
rằng
vì
các
phương
trình
vi
phân
B.24,
B.27
và
B.28
là
tuyến
tính,
và
giải
pháp
được
đưa
đến
trong
phương
trình
B.25
chủ
yếu
là
đáp
ứng
vơi
một
xung
đơn
vị
(
không
gian)
tại
gốc
(đặt
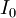 =
=
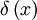 ),
sau
đó
lý
thuyết
hệ
thống
tuyến
tính
mô
tả
giải
pháp
cho
phương
trình
B.27,
(hoặc
B.28),
như
),
sau
đó
lý
thuyết
hệ
thống
tuyến
tính
mô
tả
giải
pháp
cho
phương
trình
B.27,
(hoặc
B.28),
như
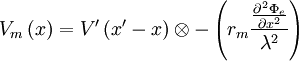 (B.29)
(B.29)
ở
đây
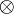 chú
thích
cho
tích
chập.
(yếu
tố
thêm
vào
chú
thích
cho
tích
chập.
(yếu
tố
thêm
vào
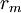 được
yêu
cầu
để
chuyển
vế
phải
của
B.28
thành
một
mật
độ
dòng.)
Hoạt
động
của
tích
chập
có
thể
được
tạo
ra
bằng
cách
lấy
biến
đổi
Fourier
nghịch
đảo
của
việc
tạo
ra
biến
đổi
Fourier
của
được
yêu
cầu
để
chuyển
vế
phải
của
B.28
thành
một
mật
độ
dòng.)
Hoạt
động
của
tích
chập
có
thể
được
tạo
ra
bằng
cách
lấy
biến
đổi
Fourier
nghịch
đảo
của
việc
tạo
ra
biến
đổi
Fourier
của
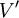 và
của
đạo
hàm
bậc
hai
của
và
của
đạo
hàm
bậc
hai
của
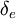 .
Hoạt
động
này
được
tiến
hành
dễ
dàng
bằng
cách
sử
dụng
biến
đổi
Fourier
nhanh.
.
Hoạt
động
này
được
tiến
hành
dễ
dàng
bằng
cách
sử
dụng
biến
đổi
Fourier
nhanh.
B.7 Những phương trình rút gọn của Maxwell trong chế phẩm sinh lý ở phạm vi ngoài nguồn
Điều kiện đầu:
Nguồn
và
Trường:
Bán
tĩnh
(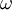 <1000
Hz)
<1000
Hz)
Bộ
dẫn
khối:
hữu
hạn
giới
hạn
(r
<
1m)
phạm
vi
ngoài
nguồn
trở
kháng
không
đồng
nhất
(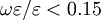 )
)
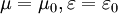 .
.
Cuối cùng chúng tôi thu thập những phương trình của Maxwell trong dạng đơn giản nhất của chúng. Những phương trình này hợp lệ dưới điều kiện sinh lý điện bán tĩnh ngoài phạm vi của nguồn điện sinh học:
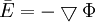 (B.23)
(B.23)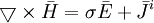 (B.10)
(B.10)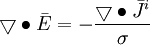 (B.11)
(B.11)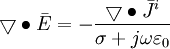 (B.9)
(B.9)tham khảo
Barr RC, Spach MS (1977): Sampling rates required for digital recording of intracellular and extracellular cardiac potentials. Circulation 55: 40-8. Maxwell J (1865): A dynamical theory of the electromagnetic field. Phil. Trans. R. Soc. (Lond.) 155: 459-512. Maxwell J (1873): Treatise On Electricity and Magnetism, Vol. 2, Oxford. (Reprint by Dover, New York, 1954.) Plonsey R, Collin R (1961): Principles and Applications of Electromagnetic Fields, 554 pp. McGraw-Hill, New York. Plonsey R, Heppner DB (1967): Considerations of quasistationarity in electrophysiological systems. Bull. Math. Biophys. 29:(4) 657-64. Schwan HP, Kay CF (1957): The conductivity of living tissue. Ann. N.Y. Acad. Sci. 65: 1007.
| Trang trước | Phụ lục B | Trang cuối |


