Sách:Điện từ sinh học/Từ tâm đồ

20.Từ tâm đồ

20.1. Giới thiệu

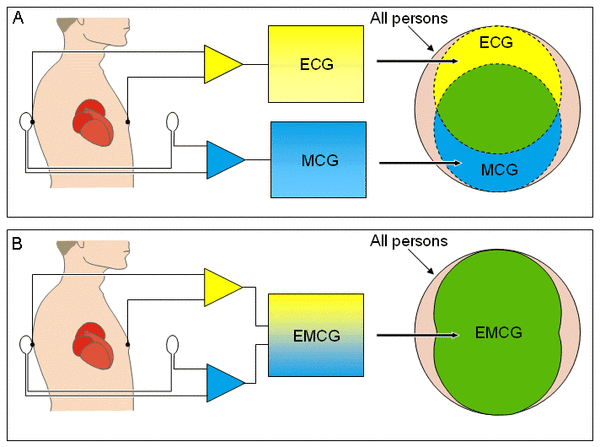
Năm 1963, hai nhà khoa học Baule và McFee đã lần đầu tiên phát hiện ra tín hiệu điện điện sinh học bằng từ tâm đồ (MCG). Phát hiện mới này mang lại tín hiệu lạc quan cho các nhà khoa học,người ta tin rằng MCG có thể thu được tín hiệu điện tim như máy điện tim ECG .Mặc dù theo lý thuyết và thực nghiệm thì nó là điều không thể thực hiện được, MCG phải dùng rất nhiều điện cực (Rush, 1975). Ở phần 2.7 ta sẽ tìm đề cập thêm về vấn đề này,trong đó người ta kết hợp sử dụng ECG và MCG (EMCG),do đó người ta có thể giảm được một nửa khả năng chẩn đoán sai các bệnh về tim mạch so với trước đây khi sử chỉ sử dụng ECG.

Năm 1970, Baule và McFee đã đưa ra lý thuyết về trường vector từ tim. Nhờ đó, các nhà khoa đã phát triển thành vector từ tâm đồ (trong đó tim được coi như một lưỡng cực từ). Ngày nay,với công nghệ hiện đại nhưng khi nghiên cứu về MCG người ta vẫn phải dựa vào sơ đồ cấu tạo cơ bản đầu tiên về từ tâm đồ.

Hiện nay ,các nhà khoa học vẫn đang thử nghiệm thêm những ứng dụng của MCG, như nghiên cứu thêm về sự đột tử do nhồi máu cơ tim hay sự đào thải của tim đối với các thiết bị cấy từ bên ngoài.

Trong chương này chúng ta sẽ chủ yếu tìm hiểu về các ứng dụng của lưỡng cực tương đương hai chiều đối với tim và mối quan hệ giữa ECG-MCG.

20.2. Những phương pháp cơ bản trong từ tâm đồ

20.2.1. Đo lưỡng cực từ tương đương hai chiều

Các điều kiện đầu:

Nguồn:Lưỡng cực hai chiều tại một vùng cố định.

Bộ dẫn:Có hạn,bộ dẫn khối thuần nhất (có thể không thuần nhất).

Bảng 17.1 là danh sách các mô hình nguồn và bộ dẫn ,ta có thể coi chúng như các đạo trình điện tâm đồ khác nhau. Từ bảng này, ta có thể biết được điện tâm đồ trong y học hiện đại (với 12 đạo trình chuẩn và hệ thống vector điện tâm đồ Frank(VECG)),một lưỡng cực được giữ cố định để dùng như mô hình nguồn điện tim.Thể tích bộ dẫn coi như không đáng kể trong 12 đạo trình ECG (hay có giới hạn) và đồng nhất trong VECG.

Từ tâm đồ được dùng để hỗ trợ đo hoạt động điện của tim. Do đó mô hình nguồn và bộ dẫn của từ tâm đồ phải cùng cấp độ với đồ điện tim. Nghĩa là trong ứng dụng y học mô hình nguồn là lưỡng cực từ. Bộ dẫn có thể thay đổi được do sự biến đổi của cơ tim và lượng máu bên trong nó.

Tín hiệu từ tâm đồ thu được hiển thị trên màn hình gồm ba thành phần như dạng hàm vô hướng thời gian, hay dạng vòng lặp vector. Trong đó dạng hiển thị vòng lặp vector là quan trọng nhất, vector tín hiệu từ tim là cơ sở cơ bản của hệ thống từ tâm đồ (hình 20.1).

Hình 20.1 Lưỡng cực từ là cơ sở cơ bản của hệ thống đo từ tâm đồ.

20.2.2. Phương pháp ánh xạ từ trường

Các điều kiện đầu:

Nguồn: Nguồn phân phát

Bộ dẫn: Vô hạn,đồng nhất.

Năm 1887, Augustus Waller đã nghiên cứu và tìm ra từ tâm đồ người. Sau đó ,người ta ứng dụng nó trong kĩ thuật phát xạ ánh xạ điện thế trên bề mặt ngực. Tuy nhiên trong ứng dụng y học nó vẫn chỉ là công cụ để nghiên cứu.

Tương tự, trong từ tâm đồ phương pháp từ trường phát xạ quanh ngực cũng chỉ là công cụ nghiên cứu cơ bản. Tuy nhiên, từ trường là một đại lượng vector có ba hướng trong không gian nên phương pháp phát xạ được ứng dụng để biểu thị các hướng thành phần của từ trường xung quanh ngực. Nó cũng được ứng dụng để biểu thị trên ô tọa độ trung tâm. Năm 1972, lần đầu tiên Cohen và McCaughan đưa ra dạng biểu diễn ô tọa độ. Sau đó ,người ta đưa nó về dạng chuẩn (Karp, 1981) gồm 6×6 vùng đo trên lồng ngực trước.

Theo thuyết trường đạo trình, phương pháp phát xạ thường đưa ra những tín hiệu bị méo được sinh ra từ bộ dẫn không đồng nhất ( giống với trạng thái làm việc của trường điện thế phát xạ). Người ta nhận ra rằng nếu sử dụng phương pháp cảm biến điện tử phát xạ sẽ làm giảm tỉ lệ nhiễu và có thể vận dụng dễ dàng.

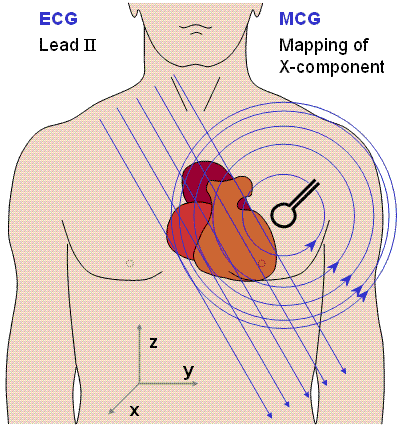(20.2)

Hình 20.2 Hình minh họa điểm tương tự giữa đạo trình điện trường và đạo trình từ trường. Nếu như từ trường được đo là đại lượng có hướng và cố định ,có trục đối xứng đặt xa so với tim thì trường đạo trình từ giống với trường đạo trình điện (ví dụ như đạo trình II),có trục đối xứng và tín hiệu thu được tương tự nhau.

20.2.3. Các phương pháp khác của từ tâm đồ

Để phân tích các chỉ số của tín hiệu MCG ta có thể dùng phương pháp xác định lưỡng cực từ tương đương hay phương pháp phát xạ,ngoài ra ta có thể áp dụng thêm một số phương pháp kĩ thuật. Ở đây chúng ta sẽ tìm hiểu về phương pháp định vị nguồn điện tim.

Định vị nguồn điện tim là phương pháp xác định những chỗ dị thường của tim hay những đường mạch dẫn trong nó. Nó có thể gây lên chứng loạn nhịp hay suy giảm hoạt động của tim. Ví dụ như trong đường mạch dẫn ở tim, điện tích hoạt động truyền trực tiếp từ cơ tâm nhĩ tới cơ tâm thất qua lớp chuyển tiếp tâm nhĩ thất ( AV junction). Người ta gọi nó là hội chứng Wolff-Parkinson-White hay WPW. Nếu một đường mạch dẫn từ khối tâm thất trở lại khối tâm nhĩ bị thoái hóa, nó sẽ làm tim đập nhanh hơn bình thường. Nếu khi dùng thuốc mà triệu chứng vẫn không kiểm soát được thì ta phải đưa bệnh nhân đi phẫu thuật. Do đó việc đầu tiên cần làm là giữ ổn định chu kì tim.

Trong nghiên cứu lâm sang ,việc định vị đường mạch dẫn theo cách thong thường phải mất vài tiếng đồng hồ. Để rút ngắn thời gian, người ta dùng một nguồn định vị đường dẫn tương đương bằng cách xác định điện thế trên bề mặt ngực. Bạn có thể tìm hiểu thêm phương pháp này trong cuốn sách của Gulrajani, Savard, và Roberge (1988).

Trong từ tâm đồ ,mục đích là để thay thế phương pháp định vị bằng cực điện bằng các phương pháp định vị từ. Phương pháp này có thể cải thiện được tính chính xác và những hạn chế của phương pháp sử dụng cực điện. Trong từ tâm đồ ,người ta định vị bằng cách lập bản đồ xác định khoảng 30-40 vị trí ở bề mặt trước của tim nhờ sử dụng đồng hồ đo từ đơn kênh và đồng hồ đa kênh. Phương pháp định vị sử dụng mô hình lưỡng cực điện là phương pháp cho kết quả rõ nhất. Bằng cách sử dụng mô hình bốn cực càng làm tăng tính chính xác của phương pháp hơn (Nenonen et al., 1991a). Độ chính xác còn phụ thuộc rất lớn vào sự chính xác của thể tích mạch dẫn. Độ sai lệch của đường mạch dẫn thực tế không quá 2-3cm so với yêu cầu.Bởi vì phương pháp định vị trong từ não đồ đòi hỏi tính chính xác ,phức tạp và giá cao hơn rất nhiều so với phương sử dụng cực điện. Ngày nay trong ứng dụng lâm sàng nó ngày càng được sử dụng phổ biến.

20.3 Phương pháp xác định vector từ tim

20.3.1 Mô hình bộ dẫn, nguồn và dạng hệ thống đạo trình cơ bản để đo lưỡng cực từ

Các điều kiện đầu:

Nguồn: Phân phát

Bộ dẫn: Giới hạn, dạng cầu, thuần nhất,vùng dẫn của tim cách điện với vùng phổi

Trong phần này tìm hiểu này, chúng ta giả định coi tim là vùng dẫn cầu, cách điện với phổi. Giả thiết rằng quả tim là một khối hình trụ đối xứng với ba thành phần thỏa mãn hệ thống đạo trình XYZ và ABC, trong đó mỗi đạo trình tương ứng với bộ dẫn có thể tích hình trụ đối xứng với ba thành phần đo trực giao nhau. Thành phần x và y trong hệ thống đạo trình không cần có vị trí cố định. Giả thiết rằng có một trường lực tim chạy theo hướng tiếp tuyến vào trong tim. Người ta gọi đó là hiệu ứng self-centering (Baule and McFee, 1970). Đây cũng là một khái niệm trong giải phẫu.

Trước đó, ở phần 12.5, theo định nghĩa moment dòng phát hữu hạn của lưỡng cực từ , thể tích bộ dẫn thuần nhất so với ban đầu (Stratton, 1941) là:

(20.1)

Tương tự , với bộ dẫn có thể tích thuần nhất ,vô hạn, moment lưỡng cực từ của dòng phát theo hướng là:

Trong phần 12.6, ta thấy hệ thống đạo trình xác định moment lưỡng cực từ này có ba thành phần trực giao nhau. Với mỗi hướng thành phần sẽ có một dòng đảo, và một từ trường đảo qua nguồn. Từ trường đảo này sẽ sinh ra dòng từ có độ lớn tỉ lệ với khoảng cách so với trục (hình 20.3).

Hơn nữa ,trong phần 12.7 còn cho ta một phương pháp đơn giản để xác định hệ thống đạo trình dung để đo cực đơn hoặc lưỡng cực trên các trục tọa độ (Malmivuo, 1976) , được biểu diễn trên hình 20.4.

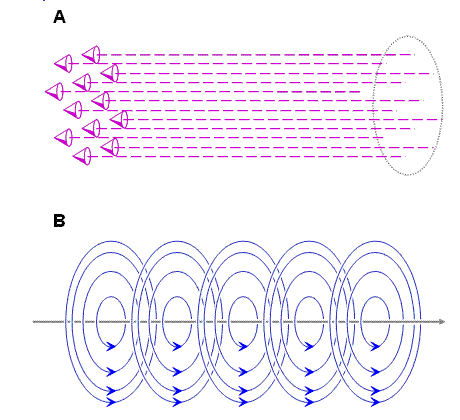
Hình 20.3 (A) Một thành phần từ trường đảo LM và hướng của nó

(B) Một thành phần của trường đạo trình LM của một hệ thống đạo trình lý tưởng dùng để xác định moment lưỡng cực từ của nguồn.Mỗi hệ thống đạo trình sẽ có ba thành phần trực giao.

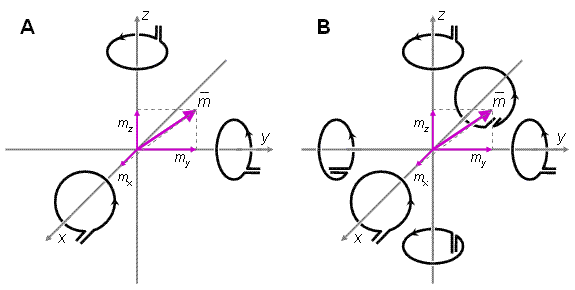
Hình 20.4 Một phương pháp đơn giản để xác định moment lưỡng cực từ của nguồn tại các thành phần x-,y- và z- của từ trường trên trục tọa độ. Có thể đo bằng đơn cực (A) hoặc lưỡng cực (B).20.3.2 Hệ thống đạo trình Baule-McFee

Gerhard M. Baule và Richard McFee là những người đầu tiên đưa ra khái niệm về vector từ tim và phương pháp xác định năm 1970. Trong một bài báo (Baule and McFee, 1970) , các tác giả đã giới thiệu một thiết bị dùng để đo từ trường tim. Hệ thống này được miêu tả trong hình 20.5.

Hệ thống đạo trình được thiết kế cho máy đo từ dùng cuộn cảm lõi sắt từ tốt hơn so với máy đo từ lõi SQUID (ở đây không đề cập đến). Nó kết hợp sử dụng mười cuộn để đo các lưỡng cực của ba thành phần trực giao của vector điện tim cùng một lúc.

Hình 20.5A miêu tả cấu trúc cơ bản của cuộn cảm lõi sắt từ trong hệ thống. Hình 20.5B minh họa phương pháp đo thành phần theo phương x. Ở đây người ta đặt lõi sắt ở trung tâm. Trong hình biểu diễn sự sinh ra từ trường đảo theo phương trục x bên trong vùng tim. Khi thay máy phát dòng đảo bằng bộ khuếch đại ,theo thuyết trường đạo trình ,có thể xác định được thành phần x của vector từ tim. Phương pháp đo thành phần y được minh họa trong hình 20.5C. Trong hình biểu diễn sự sinh ra của từ trường đảo theo hướng trục y bên trong vùng tim. Tương tự, việc xác định thành phần theo hướng z được minh họa trong hình 20.5D.

Hệ thống đạo trình Baule và McFee không thể thực hiện được do nhiễu từ xung quanh nên nó không thể xác định được MCG. Mục đích của hệ thống là để chứng minh có thể xác định được vector từ tim.

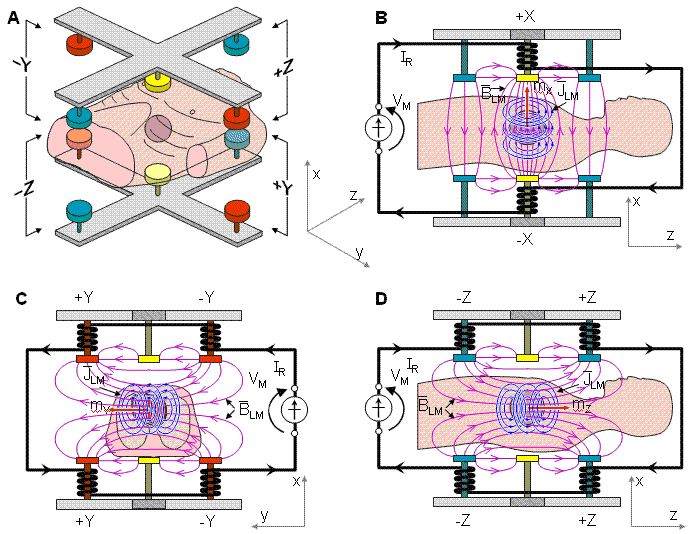
Hình 20.5 Hệ thống đạo trình Baule-McFee

(A) Hệ thống đo thông thường

(B) Xác định thành phần x của vector từ tim.

(C) Xác định thành phần y của vector từ tim.

(D) Xác định thành phân z của vector từ tim.

20.3.4 Hệ thống đạo trình ABC

Malmivuo (1976) đã đưa ra một phương pháp để tránh những khó khăn gặp phải trong việc ứng dụng hệ thống đạo trình XYZ. Nếu hệ 3 trục trực giao được lựa chọn sao cho chúng trùng với các cạnh của một hình lập phương, trong đó trục chéo là trục x (từ sau ra trước) và gốc tọa độ nằm ở vị trí trung tâm của quả tim, chúng ta sẽ nhận được một hệ trục có hướng đối xứng so với cơ thể hơn.Hệ trục này được gọi là hệ trục ABC và được chỉ ra trong Phụ lục A.

Hệ thống đạo trình ABC thu được từ hệ thống XYZ bằng cách căn các từ kế dọc theo các tọa độ ABC. Hình 20.7 minh họa hệ thống đạo trình ABC trong dạng đối xứng (lưỡng cực). Hệ thống đạo trình ABC cũng có thể được áp dụng một cách không đối xứng (đơn cực) bằng cách quản lý các phép đo chỉ ở mặt trước của ngực. Trong trường hợp này, các phép đo có thể được thực hiện ở gần tim hơn, do đó tỉ số SNR sẽ tăng. Tuy nhiên, chất lượng của các trường đạo trình trong trường hợp này lại giảm đi, do chúng không đều khi xuyên qua.

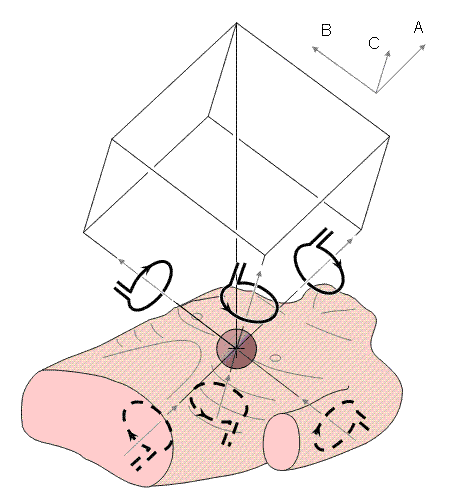
Hình 20.7 Hệ thống đạo trình lưỡng cực ABC.

20.3.5 Hệ thống đạo trình đơn điểm

Trong việc ứng dụng phép đo SQUID, vị trí riêng rẽ của mỗi từ kế được xem là nhược điểm chính do giá của nhiều từ kế sẽ cao hoặc làm tăng thời gian đo khi đặt chỉ 1 từ kế liên tiếp tại các điểm riêng rẽ. Trong năm 1976, Malmivuo đã giới thiệu một hệ thống đạo trình thứ 3, gọi là hệ thống đạo trình đơn điểm, có thể tránh được khó khăn của phép đo đa điểm. Trong dạng không đối xứng (đơn cực), có thể nhận ra hệ thống này với một bình đơn đựng heli lỏng bởi vì 3 cuộn dây (hoặc các hệ thống đo trường năng lượng) được đặt ở cùng 1 vị trí. Đây là một cải tiến đáng kể so với các hệ thống đạo trình XYZ và ABC (Malmivuo, 1976). Thực tế là ngoài thành phần x, các thành phần y và z của vector từ tâm cũng có thể đo được từ cùng vị trí đo thành phần x với hệ thống đạo trình XYZ, dựa trên nguyên lý sau (xem hình 20.8A):

Chia dipole từ thành 3 thành phần, , , và . Chúng ta xem 3 thành phần H_x ,H_y và H_z của cường độ từ trường H trên trục x do dipole từ này tạo ra. Từ các đường sức từ, chúng ta nhận thấy rằng thành phần x của cường độ từ trường (H_x) có cùng hướng với thành phần x của dipole từ ( ). Các thành phần y và z của cường độ từ trường song song nhưng lần lượt lại ngược hướng với m_y và m_z . Hơn nữa, đối với , và m_x ,m_y và m_z có cùng độ lớn, biên độ của H_y và H_z bằng 1/2 biên độ của H_x . Đây là kết quả của các phương trình của cường độ từ trường tạo bởi dipole từ (theo hướng z) (xem hình 20.8B):

trong đó:

m= moment của dipole từ

r= vector bán kính (khoảng cách)

θ= góc giữa moment (trục z) và vector bán kính(cực)

φ= góc quanh moment (trục z) (góc phương vị).

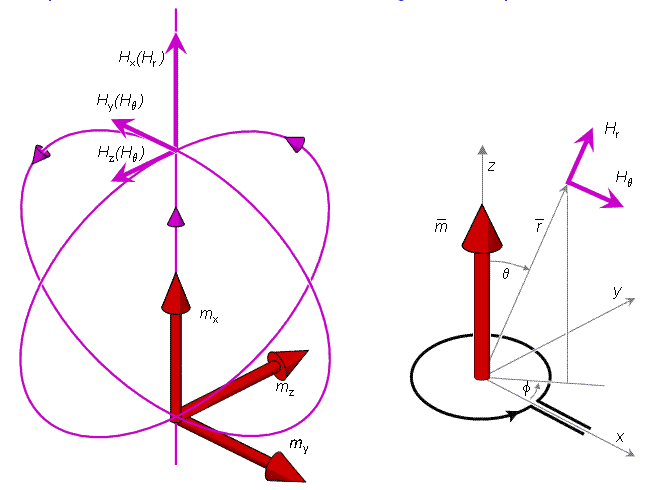
Hình 20.8 :

(A) 3 thành phần H_x, H_y, and H_z của cường độ từ trường H tạo ra bởi 3 thành phần m_x, m_y, and m_z của 1 dipole từ .

(B) Các thành phần của từ trường của 1 lưỡng cực.

Trong cách sắp xếp của hình 20.8, thành phần H_x tương ứng với H_r và 2 thành phần H_y ,H_z tương ứng với H_{θSubscript text} của phương trình 20.3.

Nguyên lý của hệ thống đạo trình đơn điểm này có thể được xem xét một cách tương tự theo trường đạo trình. Chúng ta xét cường độ từ trường đảo gây ra bởi một dòng ngược I_r đưa tới cuộn dây của từ kế. (xem hình 20.9). Độ lớn của moment lưỡng cực đối với cuộn dây 1 vòng có thể tính được theo phương trình 20.4 (các moment lớn hơn hiển nhiên có thể được bỏ qua, nếu trường đang xét nằm ở khoảng cách tương đối xa so với bán kính a của cuộn dây):

trong đó:

I= dòng trong cuộn dây

a=bán kính sợi dây

(nếu có N vòng, m = Iπa²N.). Hướng của vuông góc với mặt phẳng chứa cuộn dây.

Trong hình 20.9A, hướng của cuộn dây trong từ kế là ( θ = 0° , 180° ) do đó trục của nó sẽ xuyên qua tim, mà điểm giữa của tim trùng với gốc tọa độ. Điều này phù hợp với cách sắp xếp để đo thành phần x của vector từ tim với hệ thống đạo trình XYZ. Ở đây chỉ ra cách áp dụng phương trình 20.3 để tính cường độ từ trường đảo trong phạm vi của tim.

Phương trình 20.3 một lần nữa lại cho thấy rằng từ kế đặt trên trục x nhạy cảm hơn đối với thành phần tương tự của dipole từ tim do có sự tương ứng về hướng. Kết quả đã nói ở trước chỉ nhận được khi cuộn dây ở một khoảng cách đủ lớn đến tim so với phạm vi của tim, và chúng ta có được sự xấp xỉ hợp lý là toàn bộ điểm nằm trong tim (tương đối so với gốc đặt ở cuộn dây) có r = r, θ = 0°.

Để đo thành phần y của vector từ tim, cuộn dây của từ kế phải nghiêng 90°, do đó các điểm trong tim có thể được coi như xấp xỉ có θ = 90°, 270°, như trong hình 20.9B (như đã nói ở trên, giả sử rằng khoảng cách tới tim là đủ lớn so với phạm vi của tim). Vì vậy, cường độ từ trường trong phạm vi của tim là:

Phương trình này cũng nhận được từ phương trình 20.3 dựa trên giả sử rằng bất kì điểm nào ở trong tim cũng có tọa độ (r = r, θ = 90° ). Một lần nữa lại thấy rằng từ kế nhạy cảm đối với thành phần dipole từ của tim có cùng hướng với trục của từ kế (mặc dù trong trường hợp này là hướng ngược lại). Trường hợp đo thành phần z cũng theo một cách tương tự.

Chúng ta để ý rằng cường độ của từ trường đảo ở trong trường hợp đầu (đo thành phần x) đúng bằng 2 lần cường độ trong trường hợp sau (với thành phần y và z). Hơn thế nữa, trong trường hợp đầu, từ trường đảo có cùng hướng với dipole từ của cuộn mang năng lượng đảo. Trong trường hợp thứ 2, hướng của từ trường đảo ngược với hướng của moment lưỡng cực của cuộn dây. Do đó, khi sử dụng hệ thống đạo trình đơn điểm, sẽ nhận được 2 thành phần không hướng tâm (y và z) của vector từ tim (MHV) từ vector từ trường (MFV; tín hiệu chuyển đạo từ các cuộn dây vuông góc đôi một) bằng cách nhân với hệ số -2, như đã chỉ ra trong phương trình 20.7. Hình 20.10 minh họa sự thể hiện của hệ thống đạo trình đơn điểm.

trong đó:

MHV= vector từ tim

MFV= vector từ trường

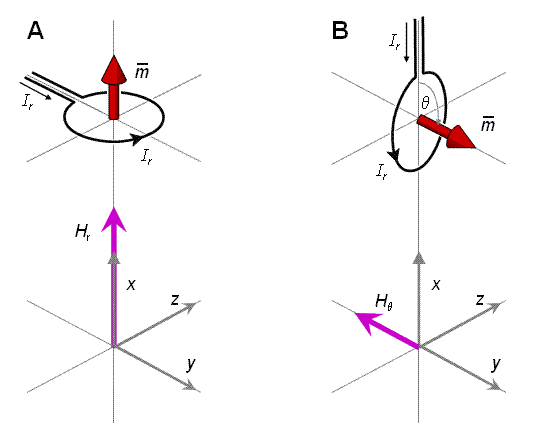
Hình 20.9 Sự hình thành từ trường đảo trong phạm vi của tim khi đo

(A) thành phần x, và

(B) thành phần y của vector từ tâm với hệ thống đạo trình đơn điểm.

Trường hợp đo thành phần z tương tự với phép đo thành phần y.

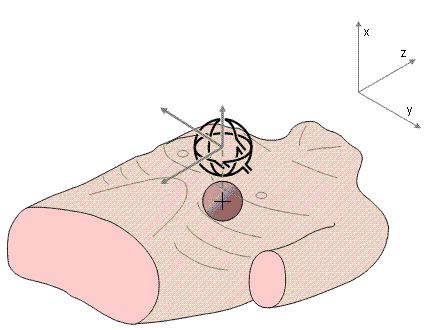
Hình 20.10 Sự thể hiện của hệ thống đạo trình đơn điểm. các mũi tên để chỉ hướng của phép đo. Quả cầu tô đậm biểu thị cho quả tim.

Hệ thống đạo trình đơn điểm đã hiệu chỉnh

Eskola và Malmivuo đưa ra một phiên bản cải tiến của hệ thống đạo trình đơn điểm không đối xứng trong năm 1983 (Eskola, 1983; Eskola và Malmivuo, 1983). Các mô hình thí nghiệm đã chỉ ra rằng, trong trường hợp đo đơn cực, sẽ nhận được một kết quả chính xác hơn khi thay thế hệ số -2 trong các thành phần không hướng tâm, bằng hệ số -1 (như trong phương trình 20.8). Sự thay đổi này được giải thích bằng hiệu ứng lân cận (xem ở phần sau), ranh giới tại ngực, và cách thức mà các sự không đồng nhất nội ảnh hưởng tới các trường đạo trình trong trường hợp đo không đối xứng:

trong đó :

MHV= vector từ tim

MFV= vector từ trường

Các thí nghiệm mẫu này cũng đánh giá vị trí tối ưu của phép đo. Có thể thấy rằng méo của trường đạo trình là nhỏ nhất khi từ kế được đặt ở khoang liên sườn thứ 4, tại rìa xương ức, tương ứng với vị trí của V2 trong 12 đạo trình chuẩn ECG. Vị trí đo này, như đã chỉ ra trong hình 20.11, cũng rất dễ đặt.

Hệ thống đạo trình đơn điểm đối xứng

Như trong hệ thống đạo trình XYZ và ABC, chất lượng của các trường đạo trình của hệ thống đơn điểm có sự cải thiện đáng kể với cách sắp xếp phép đo đối xứng (lưỡng cực). Trong hệ thống đạo trình đơn điểm đối xứng này, các phép đo được thực hiện trên cả 2 phía của tim, ở cùng một khoảng cách tới tâm của tim, nằm trên đường thẳng song song với trục x axis, ở cùng 1 vị trí chỉ ra trong hình 20.11 đối với hệ thống đạo trình đơn điểm không đối xứng. Khi đó, các tín hiệu cho các thành phần x, y, và z được lấy trung bình với quy ước chuẩn về dấu như đã làm trong các hệ thống đạo trình đối xứng XYZ và ABC.

Trong hệ thống đạo trình đơn điểm đối xứng, phương trình 20.7 là hợp lý vì từ kế ở mặt trước được đặt cách xa tim hơn và bởi vì méo trong trường đạo trình này được bù ở mức độ cao do tính đối xứng (xem hình 20.16). Sự thể hiện của hệ thống đạo trình đơn điểm đối xứng được chỉ ra trong hình 20.12.

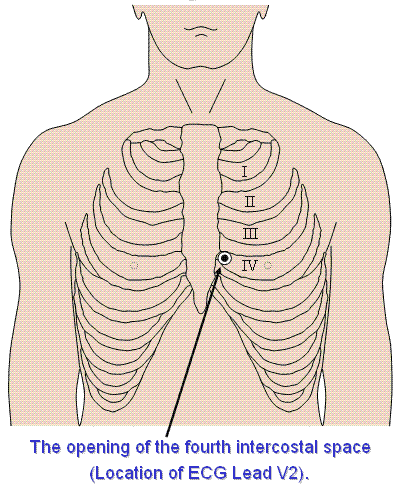
Hình 20.11 Vị trí đo của hệ thống đạo trình đơn điểm nằm ở khoang liên sườn thứ 4 tại rìa của xương ức (cùng vị trí với đạo trình thượng vị V2 của ECG).

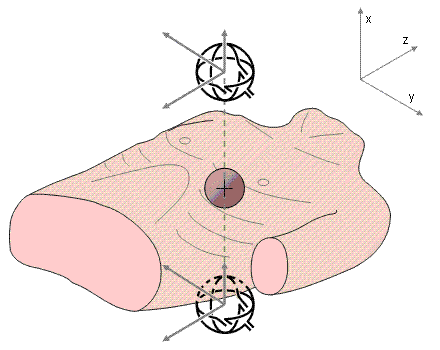
Hình 20.12 Sự thể hiện của hệ thống đạo trình đơn điểm đối xứng.

20.4 Phân bố độ nhạy của các đạo trình MCG cơ bản

20.4.1 các mô hình tim, ngực và từ kế

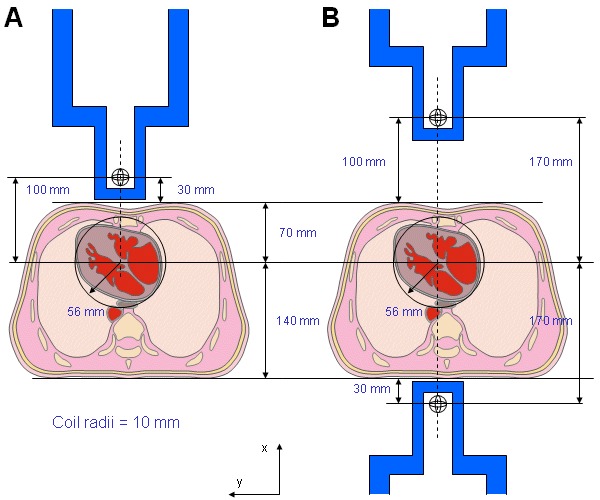
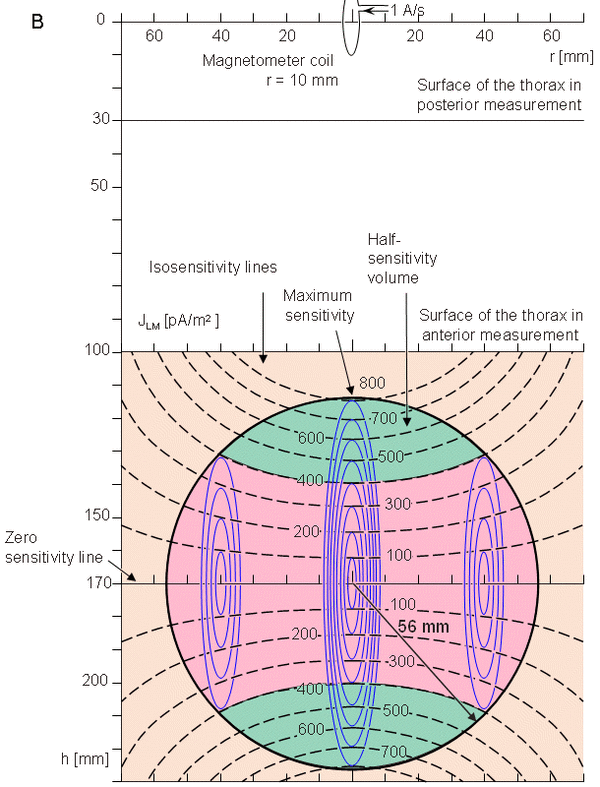
Trong phần này, sự phân bố độ nhạy của 1 từ kế đơn cuộn được tính toán theo phần 12.11. Sự phân bố độ nhạy này được xét cho trường hợp đối xứng trụ. Giả sử khoảng cách trước-sau của ngực là 210 mm và bán kính của mô hình tim hình cầu là 56 mm, được chỉ ra trong hình 20.13. Tâm của quả tim nằm cách lồng ngực trước 70 mm và 140 mm so với lồng ngực sau. Ngoài ra ta giả sử rằng bán kính của cuộn dây trong từ kế là 10 mm và khoảng cách từ tâm của nó đến lồng ngực là 30 mm. Do đó, khi từ kế được đặt ở phía trước hay sau ngực thì khoảng cách tối thiểu từ tâm của cuộn dây trong từ kế đến tâm của quả tim lần lượt là 100 mm hoặc 170 mm (Malmivuo, 1976). Các số đo này phù hợp với các phép đo đơn điểm đơn cực và lưỡng cực. Trong phần này giả sử rằng từ kế không có các cuộn bù, ví dụ như từ kế không phải làmáy đo trường năng lượng (gradiometer).

Hình 20.13 Các kích thước cho mô hình ngực và tim, và các khoảng cách đo trong phép đo đơn điểm đơn cực và lưỡng cực.

(A) vị trí đo đơn cực (không đối xứng) ở mặt trước.

(B) các vị trí đo lưỡng cực (đối xứng) ở mặt trước và mặt sau.

20.4.2 Phép đo đơn cực

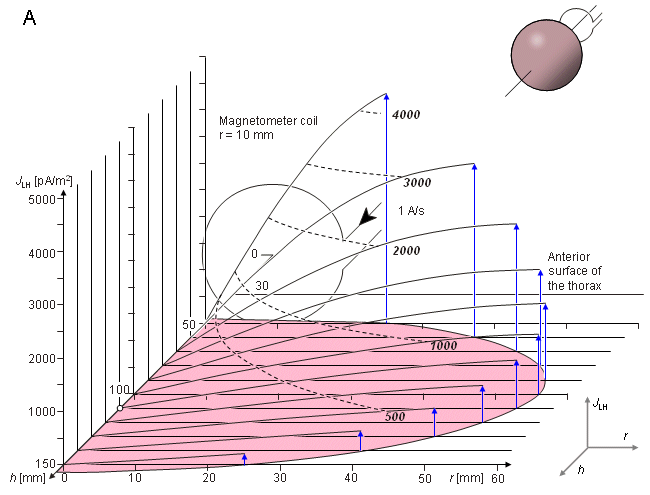
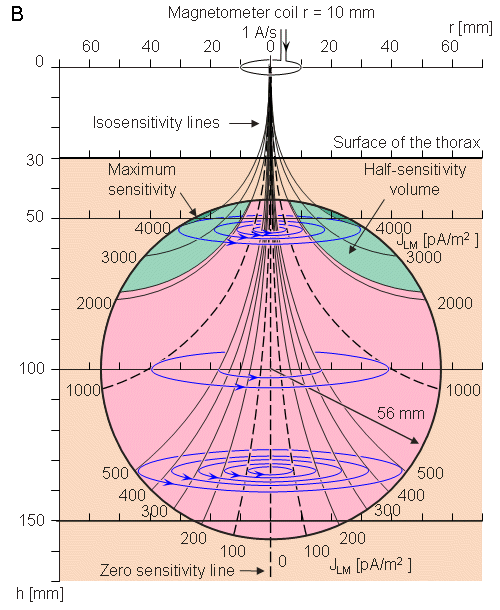
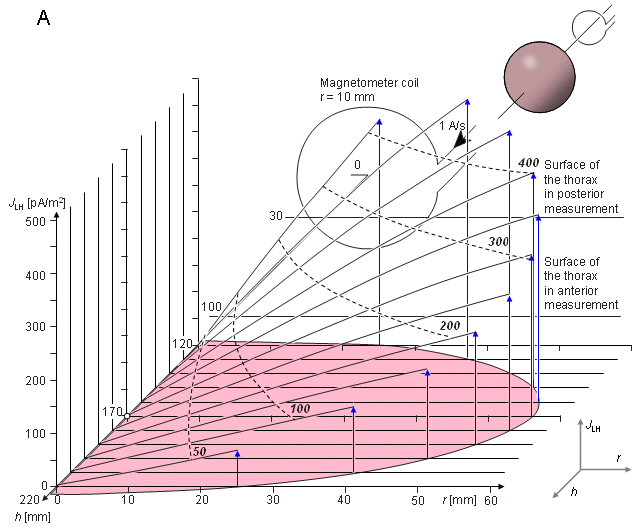
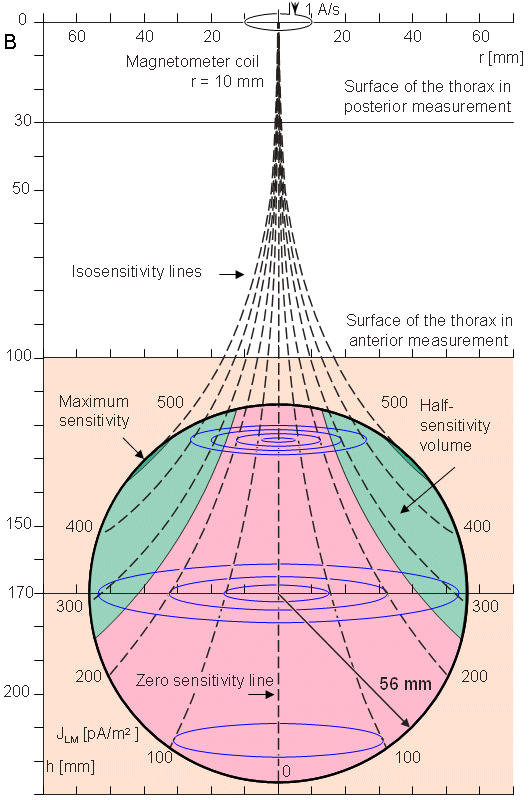
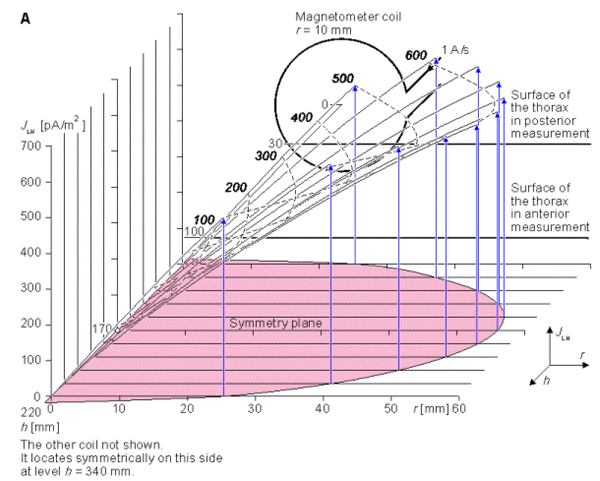
Như đã chú thích trong phần 12.11, trong trường hợp đối xứng trụ, dòng kích trường đạo trình (lead field current) có phương tiếp tuyến, và biên độ của nó độc lập với góc. Do đó, sự phân bố dòng kích trường đạo trình có thể xem như hàm của bán kính hướng tâm r từ trục đối xứng, với khoảng cách h từ từ kế là 1 tham số. Hình 20.14 minh họa sự phân bố độ nhạy bên trong phạm vi 100 mm của mô hình tim. Điều này được chỉ ra với một loạt các đường cong mô tả mật độ dòng kích trường đạo trình, là hàm của khoảng cách (hình 20.14A) và với các đường cong đẳng nhạy (isosensitivity) (hình 20.14B). Hình này cũng chỉ ra vị trí và kích thước của từ kế. Trường hợp đo này phù hợp với phép đo thành phần x của MHV sử dụng hệ thống đạo trình đơn điểm (đơn cực) không đối xứng tại phía trước ngực như đã minh họa trong hình 20.10. Hình 20.15 minh họa thông tin tương tự cho khoảng cách đo là 170 mm. Trường hợp này phù hợp với phép đo đơn cực tại phía sau của ngực.

Như có thể thấy trong hình 20.14, độ nhạy của phép đo đơn cực tập trung trên vùng trước của tim. Hiện tượng này được gọi là hiệu ứng lân cận.

Hình 20.14 Sự phân bố độ nhạy của một phép đo đơn cực (không đối xứng) bên trong phạm vi của mô hình tim với khoảng cách giữa 2 tâm là 100 mm. Trong hình cũng minh họa vị trí và kích thước của từ kế. Trường hợp đo này phù hợp với phép đo thành phần x của MHV với hệ thống đạo trình đơn điểm không đối xứng ở mặt trước ngực.

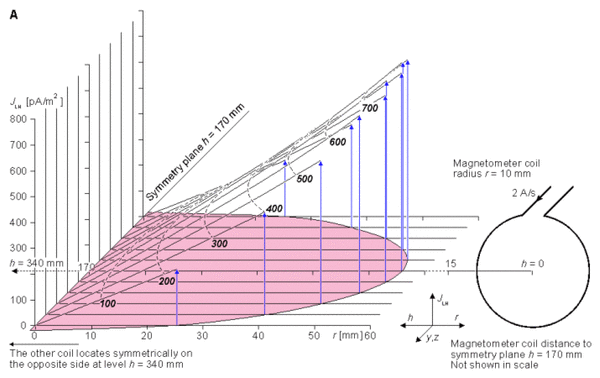
(A) Sự phân bố độ nhạy trong phạm vi của tim. Khoảng cách tới từ kế, h, và khoảng cách tới trục r không được chỉ ra.

(B) Các đường cong đẳng nhạy được minh họa bằng các đường đứt nét màu đen. Các đường mô tả dòng kích trường có màu xanh. Các kích thước h và r được biểu diễn trên thang

Hình 20.15 Sự phân bố độ nhạy của một phép đo đơn cực (không đối xứng) bên trong phạm vi mô hình tim với khoảng cách tâm-tâm giữa tim và từ kế là 170 mm. Trường hợp đo này phù hợp với phép đo thành phần x của MHV tại phía sau của ngực.

(A) Sự phân bố độ nhạy bên trong phạm vi tim. h và r không được chỉ ra trên thang.

(B) Các đường cong đẳng nhạy được minh họa bởi các đường đứt nét màu đen. Các dòng kích trường được biểu diễn bởi các đường liền nét màu xanh. Độ lớn của h và r được biểu diễn trên thang.

20.4.3 Phép đo lưỡng cực

Hiệu ứng lân cận có thể được bù bằng cách sử dụng các phép đo lưỡng cực, mà ở đó 2 phép đo được thực hiện một cách đối xứng ở 2 phía đối diện của tim. Đây là trường hợp trong các hình 20.6 và 20.7, tương ứng với các hệ thống đạo trình (lưỡng cực) đối xứng XYZ và ABC. Đó cũng là trường hợp của phép đo thành phần x với hệ thống đạo trình đơn điểm đối xứng như đã chỉ ra trong hình 20.12.

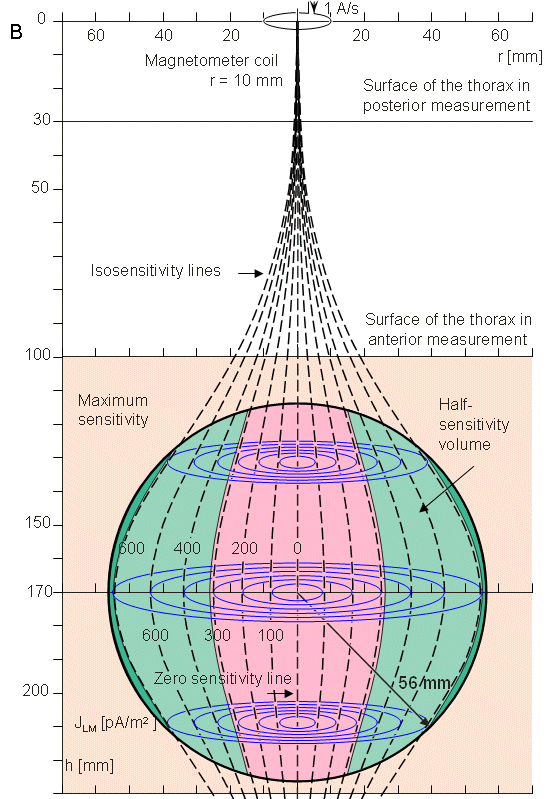
Hình 20.16 minh họa sự phân bố độ nhạy trong phép đo lưỡng cực của thành phần dọc trục của từ trường. Bán kính cuộn dây trong từ kế vẫn là 10 mm. Khoảng cách tới từ tâm của tim tới từ kế ở cả 2 phía là 170 mm, bởi vì đây là khoảng cách tối thiểu trên vùng sau của ngực. Trường hợp đo này ứng với phép đo thành phần x của MHV trên cả 2 phía của ngực với hệ thống đạo trình đối xứng XYZ hoặc với hệ thống đạo trình đơn điểm đối xứng (đối với phép đo đối xứng của các thành phần y và z trong hệ thống đạo trình XYZ và cho tất cả các thành phần của hệ thống đạo trình ABC, các khoảng cách đo sẽ phải lớn hơn.). Trong hình này, mật độ các dòng kích trường đạo trình của các phép đo ở đằng trước và đằng sau được tính đến. Điều này tương ứng với việc tính tổng các tín hiệu MCG tương ứng. Cần chú ý rằng nhiễu của các phép đo trên cũng được tính đến. Do đó, thang độ nhạy của các hình 20.15 và 20.16 là thích hợp khi so sánh với biên độ các tín hiệu nhưng sẽ là không thích hợp khi so sánh với các tỉ số SNR.

Trong phép đo các thành phần y và z của hệ thống đạo trình đơn vị trí (đơn điểm ), trường hợp này không có đối xứng trục do các trường đo không có các thành phần dọc trục. Vì vậy, chúng ta phải giả sử rằng mô hình tim là một khối dẫn hình cầu, được bao quanh bởi các mô phổi cách điện. Hình 20.17 chỉ ra sự phân bố độ nhạy trong phép đo của thành phần y. Nó được chỉ ra trong cả 2 mặt phẳng zx và yz. Trong phép đo thành phần z, cường độ từ trường đảo dĩ nhiên là tương tự. Chú ý rằng, như đã đề cập đến trong phần 20.3.5, cường độ từ trường đảo này bằng một nửa cường độ trong phép đo thành phần x. Do đó cần phải có hệ số -2 trong phương trình 20.7.

Các hình 20.16 và 20.17 minh họa rằng hiệu ứng lân cận có thể được bù một cách rất chính xác nhờ phép đo lưỡng cực (đối xứng). Bởi vì vị trí phía trước của cuộn dây trong từ kế so với bề mặt phần thân trên trong phép đo lưỡng cực ở xa hơn trong phép đo đơn cực, nên độ nhạy của nó bị giảm đi so với độ nhạy của từ kế mặt sau. Tuy vậy cách sắp xếp đối xứng (lưỡng cực) được khuyến khích bởi vì nó dẫn đến sự phân bố độ nhạy gần với lý tưởng hơn.

Hình 20.16 Sự phân bố độ nhạy của một phép đo lưỡng cực (đối xứng) trong phạm vi mô hình tim. Hình này cũng minh hoạ từ kế đo ở phía trước. Trường hợp đo này tương ứng với phép đo thành phần x của MHV dùng hệ thống đạo trình đối xứng XYZ hoặc dùng hệ thống đạo trình đơn điểm đối xứng với các phép đo ở cả 2 phía của ngực .

A) Sự phân bố độ nhạy. Phạm vi của tim được tô màu. Các khoảng cách h và r không được biểu diễn trên hình.

(B) Các đường đẳng nhạy được minh hoạ bởi các đường đứt nét màu đen. Các dòng kích trường được biểu diễn bởi các đường liền nét màu xanh. Các khoảng cách h và r được thể hiện trên thang.

Hình 20.17 Sự phân bố độ nhạy trong phép đo thành phần y sử dụng hệ thống đạo trình đơn điểm đối xứng, được minh hoạ (A) trong mặt phẳng zx và (B) trong mặt phẳng yz. Các đường đẳng nhạy được biểu diễn bởi các đường đứt nét. Các dòng kích trường được biểu diễn bởi các đường liền nét.

20.5 SỰ HÌNH THÀNH TÍN HIỆU MCG TRONG QUÁ TRÌNH HOẠT ĐỘNG ĐIỆN CỦA TIM

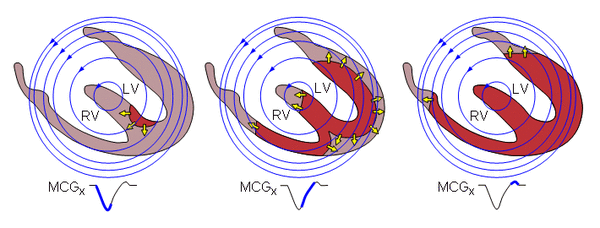
Như đã chỉ ra trong các phần trước, nguồn tạo tín hiệu MCG chính là sự hoạt động điện của cơ tim. Sự hình thành tín hiệu MCG từ quá trình hoạt động ở mặt trước quả tim có thể được minh họa một cách tương tự nhờ sự trợ giúp của các trường đạo trình MCG, như trong phần 15.2 đối với tín hiệu ECG nhờ các trường đạo trình ECG.

Trong hình 20.18, sự hình thành của tín hiệu MCG trong các đạo trình x và z đã được vẽ phác. Minh họa này chỉ là tương đối, mục đích của nó là đưa đến cho ta ấn tượng về nguyên lý tạo ra tín hiệu. Xét cho thành phần x, chúng ta giả sử rằng do hiệu ứng lân cận có ảnh hưởng mạnh nên tín hiệu tạo ra chủ yếu từ sự hoạt động của mặt trước quả tim. Xét cho thành phần z, chúng ta đã biết rằng, trong các phép đo MCG đơn điểm không đối xứng, đường có độ nhạy bằng không nằm ở mặt sau của tim. Bởi vì độ nhạy tỉ lệ với khoảng cách từ đường này nên mặt trước của tim lại chiếm phần đóng góp trội hơn.

Hình 20.18: Giản đồ minh họa của quá trình tạo thành phần x của tín hiệu MCG

20.6 MỐI QUAN HỆ ECG-MCG

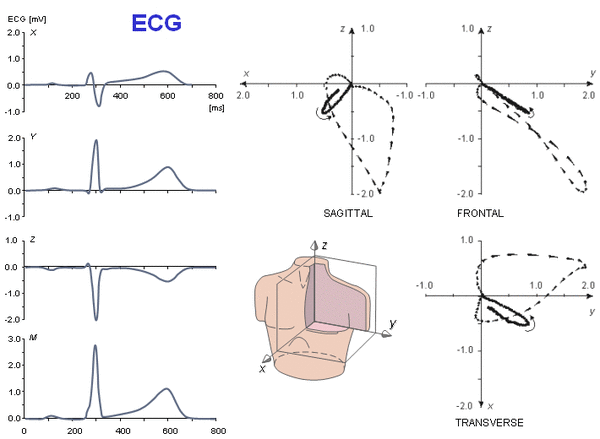
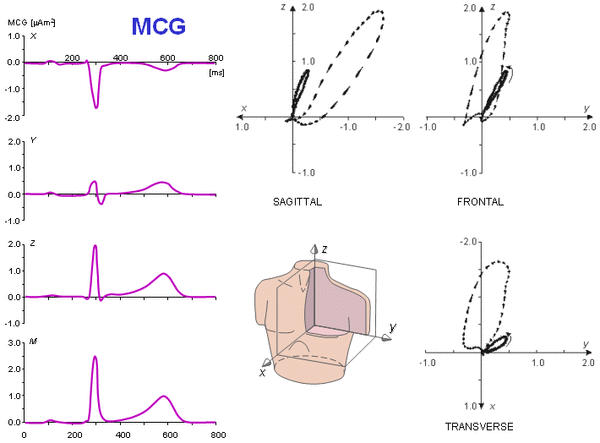
Về mặt lý thuyết, mối quan hệ giữa ECG và MCG thông thường đã được nói đến trong các phần 12.9 và 12.10. Trong phần dưới đây, chúng ta sẽ khảo sát mối quan hệ này bằng các phép đo tín hiệu thật. Hình 20.19 minh họa vector điện tim trung bình của 1 người đàn ông 30 tuổi, khỏe mạnh, được ghi lại với hệ thống đạo trình Frank. Vector từ tim trung bình cũng của người đó, được ghi lại với hệ thống đạo trình đơn điểm đã hiệu chỉnh, được minh họa trong hình 20.20 (theo Nousiainen, Lekkala, và Malmivuo, 1986; Nousiainen, 1991).

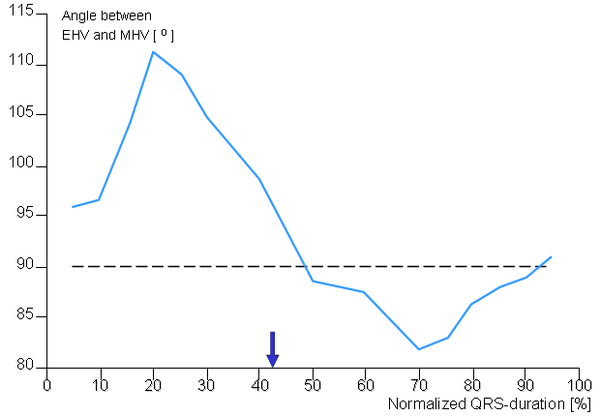
Từ các hình 20.19 và 20.20, chúng ta có thể thấy rằng tại đỉnh của đoạn sóng QRS, các vector điện tim và từ tim gần như tạo với nhau góc 90°. Điều này cũng có thể dự đoán được theo lý thuyết (theo Wikswo và các cộng sự, 1979). Nếu góc luôn chính xác đạt 90o, thì cũng không còn thông tin gì mới có thể nhận được trong MCG. Tuy nhiên, người ta đã nhận thấy góc này thay đổi đáng kể trong suốt giai đoạn sóng QRS, từ bệnh nhân tới bệnh nhân lẫn trong các sự rối loạn khác nhau của tim. Hình 20.21 chỉ cho ta thấy sự thay đổi của góc này theo thời gian, và là trị trung bình của 17 người bình thường. Mũi tên chỉ ra thời điểm đạt cực đại của đoạn sóng QRS (Nousiainen, Lekkala, và Malmivuo, 1986; Nousiainen, 1991).

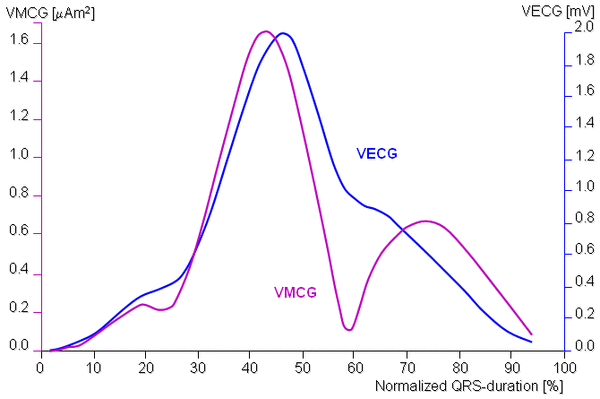
Không chỉ góc giữa vector điện tim (EHV) và từ tim (MHV) thay đổi trong giai đoạn QRS mà cả tỉ số biên độ giữa chúng cũng thay đổi. hình 20.22 sẽ minh họa cho chúng ta thấy điều này. Chúng ta có thể nhìn thấy 3 đỉnh trong đường cong biên độ MHV, được đặt tên là M1, M2, M3. Chúng ta đã đề cập trong phần 18.3, đỉnh M1 được tạo nên bởi lực hướng tâm, M2 tạo bởi lực hướng tâm và lực tiếp tuyến, còn M3 chủ yếu được tạo nên bởi các lực tiếp tuyến. như đã chỉ ra trong các phần trước, trong trường hợp lý tưởng, đạo trình điện nhạy cảm với các lực hướng tâm như với các lực tiếp tuyến, nhưng đạo trình từ lại chỉ nhạy với các lực tiếp tuyến.

Hình 20.22 minh họa một cách rõ ràng bằng cách nào mà phép đo điện, nhạy cảm hơn với các lực điện hướng tâm, lại có thể xác định được đỉnh M1 với một độ nhạy tương đối cao hơn. Đỉnh M3, tạo nên chủ yếu bởi các lực điện tiếp tuyến, được nhận biết hoàn toàn riêng biệt trong phép đo. Tuy nhiên, tại thời điểm bắt đầu của đỉnh này, tín hiệu điện lại lớn hơn. Nguyên nhân của vấn đề này vẫn chưa được làm rõ.

Hình 20.19: EHV trung bình của 1 người đàn ông 30 tuổi khỏe mạnh, ghi lại với hệ thống đạo trình Frank.

Hình 20.20: MHV trung bình của người đàn ông đó, ghi lại với hệ thống đạo trình đơn điểm đã hiệu chỉnh.

Hình 20.21 Góc tức thời giữa EHV và MHV trong khoảng thời gian đã chuẩn hoá của đoạn sóng QRS. Mũi tên chỉ ra giá trị cực đại của MHV. Đường cong là giá trị trung bình trên toàn bộ đoạn sóng QRS của 17 đối tượng.

Hình 20.22 Các đồ thị tức thời của đường cong biên độ của EHV (đường màu xanh) và của MHV trong đoạn sóng QRS .

20.7 ỨNG DỤNG LÂM SÀNG CỦA TỪ TÂM ĐỒ

20.7.1 Các ưu điểm của từ tâm đồ

Chúng ta biết rằng, hoạt động điện sinh học trong quả tim là nguyên nhân tạo ra 1 nguồn dòng, với mật độ i(x,y,z,t). Như đã nói, cả điện trường lẫn từ trường đều được hình thành bởi cùng nguồn này, và ngược lại, chúng tạo ra các hiện tượng điện sinh lý học: sự khử cực và sự tái cực của các tế bào cơ tim.

Một câu hỏi logic được đặt ra ở đây là liệu có bất kì thông tin mới nào có thể nhận được từ phép đo từ trường mà bằng phép đo điện trường chúng ta không có được? Khi câu hỏi này xuất hiện, với những cơ sở lý thuyết đã biết, đó là điện trường và từ trường không hoàn toàn độc lập với nhau, các nguyên nhân khác là nguyên lý cho việc sử dụng MCG. Chúng có thể được chia theo các đặc điểm lý thuyết và kỹ thuật. Các đặc điểm lý thuyết dựa trên các đặc tính phổ biến của từ trường sinh học, còn các đặc điểm kỹ thuật dựa trên các đặc điểm của sự trang bị dụng cụ. Chúng sẽ được đề cập đến trong phần dưới đây.

Các ưu điểm về mặt lý thuyết

Đầu tiên, bản chất của các trường đạo trình của điện và từ tương đối khác nhau, nhưng đã được mô tả trong phần 12.9. Nói chính xác, đạo trình từ lý tưởng chỉ nhạy cảm với các thành phần tiếp tuyến của các nguồn kích hoạt và do đó, nó có đáp ứng đặc biệt đối với những bất thường trong sự kích hoạt (bởi vì các nguồn kích hoạt bình thường chủ yếu là thành phần hướng tâm). Hơn nữa, các thành phần tiếp tuyến bị suy giảm trong ECG do hiệu ứng Brody. Một nhân tố khác là tỉ số SNR đối với quá trình ghi nhận điện và từ bị ảnh hưởng bởi các yếu tố khác, vì thế sẽ có ưu điểm về mặt thực tế trong việc sử dụng cái này so với cái khác, mặc dù có sự tương đồng về mặt phương pháp giữa chúng.

Hai là, độ từ thẩm của mô chính là độ từ thẩm của không gian tự do. Do đó, độ nhạy của MCG không bị ảnh hưởng bởi điện trở suất cao của mô phổi. Chính vì điều này, chúng ta có thể ghi lại độ hoạt động điện của mặt sau quả tim nhờ MCG từ phía sau của vùng ngực. Điều đó khó có thể thực hiện được bằng các điện cực ECG đặt bên ngoài, nhưng lại có thể được với một điện cực đặt trong thực quản, tuy nhiên nó lại bất tiện cho bệnh nhân. Một ứng dụng quan trọng khác của đặc điểm nổi bật này đó là ghi MCG cho thai. Trong giai đoạn nhất định của quá trình mang thai, chúng ta gặp khó khăn rất lớn trong việc ghi ECG thai do lớp mỡ cách điện trong bào thai.

Các ưu điểm về kỹ thuật

Ưu điểm đầu tiên đó là một sự khác biệt quan trọng, bộ dò từ không tiếp xúc với đối tượng. Có một lợi thế đó là không cần có quá trình chuẩn bị bề mặt da và gắn điện cực nữa. (trong trường hợp người bệnh bị bỏng da thì đây đúng là một ưu thế mấu chốt)

Thứ 2, đó là từ kế SQUID (Superconducting QUantum Interference Device- thiết bị can nhiễu lượng tử siêu dẫn) luôn có khả năng đo các tín hiệu một chiều. Chúng xuất hiện với sự lên xuống của đoạn S-T trong nhồi máu cơ tim. (Cohen et al., 1971; Cohen and Kaufman, 1975). Những tín hiệu như vậy gây ra những khó khăn lớn để có thể đo được về mặt điện. Mặc dù giá trị lâm sàng của chúng đã được chứng minh, nhưng cũng cần lưu ý rằng do những khó khăn vấp phải trong việc thực hiện phép đo điện nên có ít sự khảo sát đối với các điện thế một chiều.

20.7.2 Những nhược điểm của MCG

Có nhiều nguyên nhân dẫn đến việc ECG được sử dụng phổ biến hơn MCG. Một nguyên nhân quan trọng đó là tính dễ ứng dụng. lấy ví dụ, nếu chỉ quan tâm đến nhịp tim thì ECG thể hiện đơn giản hơn nhiều. Nguyên nhân nữa đó là việc đo MCG tại thời điểm hiện tại gặp nhiều rắc rối về mặt công nghệ và đòi hỏi thiết bị phức tạp và đắt tiền. Cụ thể, thiết bị này gồm có một từ kế SQUID, heli lỏng và một môi trường ít nhiễu. Nhờ sự phát triển của công nghệ thiết bị SQUID, hiện nay đã không còn cần một căn phòng được cách ly với bên ngoài trong MCG (trong tương lai gần, sẽ có thể thao tác các thiết bị SQUID ở nhiệt độ của nitơ lỏng, nhờ đó chi phí hoạt động sẽ giảm đi đáng kể).

20.7.3 Ứng dụng lâm sàng

Ứng dụng lâm sàng của MCG có thể dựa trên lý thuyết (điện từ trường sinh học) hoặc các đặc điểm kĩ thuật của phương pháp đo. Những lợi ích về mặt kĩ thuật chính của MCG được đề cập trong phần 20.2.1. Các điểm nổi bật về mặt lý thuyết gồm có sự phân bố độ nhạy khác biệt của MCG đối với các nguồn điện sinh học của tim.

Một số nghiên cứu về chất lượng chẩn đoán của MCG đã được công bố. Để có cái nhìn tổng quan về các nghiên cứu trên, có thể tìm đọc bài viết của Siltanen (1989). Cơ thể những người bệnh với các nhóm bệnh tim đã được khảo sát bằng ECG, bao gồm nhồi máu, phình đại và hụt dẫn. Trong hầu hết các nghiên cứu, MCG thu được với phương pháp ánh xạ bằng cách chỉ ghi lại các thành phần x của cường độ từ trường của tim tại một vài điểm ghi ở phía trên ngực mà không cần sử dụng bản chất vector của cường độ từ trường (Cohen và McCaughan, 1972; Saarinen và các cộng sự, 1978). Ngoài ra cũng có nhiều báo cáo liên quan đến việc ghi lại cả ba thành phần của trường vector từ của tim với phương pháp ánh xạ này (Cohen và Chandler, 1969; Rosen và Inouye, 1975; Seppänen và các cộng sự, 1983; Shirae, Furukawa, và Katayama, 1988; Sakauchi và các cộng sự, 1989). Trong phương pháp ánh xạ, số lượng điểm đo thường là 30-40. Nếu tín hiệu được ghi với từ kế đơn kênh (như vẫn thường được thực hiện do có kích thước của lưới đo lớn) và giả sử chúng ta có 1’ dành cho việc định vị từ kế, thêm 1’ nữa cho việc thu thập dữ liệu thì dẫn tới thời gian ghi tổng cộng cho mỗi bệnh nhân sẽ mất hơn 1h. Bằng cách sử dụng phương pháp ánh xạ cho những bất thường liên quan đến tim, chất lượng chẩn đoán của MCG, xét trung bình, cũng giống với ECG.

Ở đây, chúng tôi tổng kết một cách ngắn gọn kết quả thu được của một nghiên cứu, được thực hiện tại Học viện Ragnar Granit với sự hợp tác của Bệnh viện Đại học Tampere, là nơi nghiên cứu chất lượng chẩn đoán MCG sử dụng hệ thống đạo trình đơn điểm (Oja, 1993). Có tổng cộng 526 đối tượng được lựa chọn, trong đó có 290 người khỏe mạnh và 236 người có các rối loạn hoạt động tim, bao gồm các chứng nhồi máu cơ tim, phình đại tâm thất trái, hụt dẫn tâm thất và hội chứng Wolf-Parkinson-White. Phép phân tích thống kê biệt số tuyến tính bậc thang đã được dùng để đánh giá chất lượng chẩn đoán của VECG (sử dụng hệ thống đạo trình Frank) và VMCG được thực hiện.

Sự sai khác của VMCG trong các đối tượng bình thường và ảnh hưởng của thể chất được nghiên cứu đầu tiên bởi Nousiainen và các cộng sự (Nousiainen, 1991; Nousiainen, Oja, và Malmivuo, 1994ab). Và kết quả của nghiên cứu này đã hình thành nên cơ sở cho việc đánh giá kết quả của quá trình chẩn đoán của VMCG.

Chất lượng chẩn đoán của VECG và VMCG lần đầu tiên được so sánh về khả năng phân biệt giữa 5 nhóm, gồm (1) các đối tượng khỏe mạnh; và các bệnh nhân với (2) chứng nhồi máu cơ tim vách trước, (3) nhồi máu cơ tim dưới, (4) nhồi máu cơ tim bên, và (5) chứng phì đại tâm thất trái. Khi sử dụng VECG, các kết quả nhận được là tối ưu khi tổng cộng 30 thông số từ vector QRS và đoạn ST-T được sử dụng. Trong VMCG, các kết quả tối ưu nhận được với việc sử dụng 11 thông số từ vector QRS và 2 từ đoạn ST-T. Trong những điều kiện như trên, độ nhạy (ví dụ như phần trăm phân loại chính xác) của VECG và VMCG là như nhau, bằng 73.7%.

Chúng ta có thể tăng tốc độ phân loại 5 nhóm đã nói ở trên một cách đáng kể khi chọn 1 phần trong 30 thông số từ ECG và phần còn lại từ MCG. Với sự kết hợp này, tốc độ phân loại chính xác lên tới 81.4%. Sự cải thiện chất lượng chẩn đoán này dựa trên cơ sở thực tế là các đạo trình MCG độc lập với các đạo trình ECG. Do đó, mặc dù ECG và MCG đều có cùng chất lượng chẩn đoán và số lượng bệnh nhân được chẩn đoán chính xác là như nhau, nhưng những nhóm phân loại lại không giống nhau. Bằng việc kết hợp ECG và MCG, được gọi là EMCG (electromagnetocardiogram-điện từ tâm đồ), chúng ta có thể kết hợp các nhóm bệnh nhân được chẩn đoán đúng, như minh họa trong hình 20.23.

Trên cơ sở của nghiên cứu này và các bài viết về những nghiên cứu khác hiện có, chúng ta có thể rút ra những kết luận liên quan đến chất lượng chẩn đoán của MCG như sau:

1. mặc dù phép đo MCG đơn điểm chỉ thực hiện ở một vị trí duy nhất, so với 30-40 điểm đo trong phương pháp ánh xạ, chất lượng của phương pháp này ít nhất cũng tốt như chất lượng của hệ thống ánh xạ. 2. không có chênh lệch nào đáng kể giữa chất lượng chẩn đoán của MCG khi so sánh với ECG của Frank. 3. các cách phân loại chẩn đoán của ECG và MCG không giống nhau. (nghĩa là các đối tượng cá thể được phân loại trong từng nhóm không hề như nhau ở cả 2 phương pháp mặc dù số lượng các bệnh nhân được chẩn đoán đúng là bằng nhau.) 4. chất lượng chẩn đoán của EMCG tốt hơn ECG hoặc MCG riêng lẻ, mặc dù EMCG sử dụng cùng một số lượng các thông số như trong ECG hoặc MCG. Trong điều kiện tốt nhất, EMCG, bằng cách kết hợp dữ liệu điện và từ, có thể giảm số lượng bệnh nhân bị phân loại sai xuống còn khoảng một nửa.

20.7.4 Cơ sở cho việc tăng chất lượng chẩn đoán bằng phép đo từ sinh học

Ý tưởng cơ bản đằng sau việc tăng chất lượng chẩn đoán khi áp dụng phép ghi điện từ tâm đồ (mục 4 ở trên) là nền tảng của việc ứng dụng các phương pháp từ sinh học cho chẩn đoán lâm sàng nói chung và được nói rõ hơn ở phần dưới đây.

Nếu các đạo trình MCG là sự kết hợp tuyến tính của các đạo trình ECG (như trường hợp trong hình 20.3), thì các nhóm bệnh nhân được chẩn đoán đúng phải là như nhau trong cả 2 lần kiểm tra. Như trường hợp được minh họa bởi Willems và Lesaffre (1987), những người đã chỉ ra rằng ECG 12 đạo trình và VCG Frank có cùng chất lượng chẩn đoán. Việc kết hợp những hệ thống đạo trình này không làm tăng chất lượng chẩn đoán. Điều đó là tất nhiên, bởi vì một trong số những hệ thống đạo trình này là một sự tổ hợp tuyến tính của hệ thống khác.

Nhưng, theo như lý thuyết của Helmholtz chỉ ra, các đạo trình ECG và MCG là độc lập về mặt toán học. Do đó, các cơ thể người bệnh được chẩn đoán đúng với cả 2 phương pháp có số lượng như nhau, nhưng không giống nhau. Bởi vậy với sự kết hợp của các tín hiệu ECG và MCG, chúng ta có thể liên kết các nhóm bệnh nhân được chẩn đoán đúng và tăng được chất lượng chẩn đoán mà thậm chí không cần tăng số lượng các thông số trong quá trình chẩn đoán. Điều này là kết quả của một thực tế, đó là trong phương pháp kết hợp, chúng ta có 3 + 3 = 6 đạo trình độc lập nếu cả ECG và MCG đều dựa trên mô hình lưỡng cực.

Nguyên lý này được minh họa trong hình 20.23, trong đó toàn bộ dân số được biểu thị bởi vòng tròn lớn. giả sử rằng các bệnh nhân chẩn đoán đúng với ECG có thể được biểu thị bằng 1 vòng tròn nhỏ hơn ở bên trong, và những người được chẩn đoán đúng với MCG có thể được biểu thị bằng 1 vòng tròn tương tự. Nếu các hệ thống ECG và MCG có số lượng các phép đo độc lập bằng nhau (ví dụ, cả 2 đều dựa trên mô hình lưỡng cực), chất lượng chẩn đoán của chúng là tương đương nhau, và do đó diện tích của các vòng tròn biểu thị cho số bệnh nhân được chẩn đoán đúng với từng hệ thống là như nhau.

Bởi vì chúng ta không biết những bệnh nhân nào được chẩn đoán đúng với ECG mà lại bị sai với MCG, hoặc ngược lại, với từng hệ thống chẩn đoán riêng rẽ dùng ECG và MCG, chúng ta không thể tăng chất lượng chẩn đoán tổng cộng. (nếu chúng ta có thể biết những bệnh nhân nào được chẩn đoán đúng, bệnh nhân nào bị chẩn đoán sai, thì chất lượng chẩn đoán dĩ nhiên sẽ là 100%!). Chất lượng chẩn đoán tổng cộng chỉ có thể tăng lên nếu quá trình chẩn đoán bao gồm cả tín hiệu điện và từ trong việc hình thành phép đo điện từ tâm đồ (EMCG). Chất lượng chẩn đoán của hệ thống kết hợp do đó sẽ là vùng được bao bởi cả 2 vòng tròn ECG và MCG.

Đây là nguyên lý cơ bản đằng sau việc tăng chất lượng chẩn đoán, đạt được với một phương pháp từ sinh học cộng với chất lượng của một phương pháp điện sinh học. Nguyên lý này không những chỉ có thể ứng dụng với phép đo từ tâm đồ mà còn có thể được ứng dụng với phép đo từ não đồ và cả trong những lĩnh vực khác liên quan đến từ sinh học.

Hình 20.23 Minh hoạ nguyên lý tăng chất lượng chẩn đoán bằng việc sử dụng các phép đo từ sinh học.

(A) Nếu các phương pháp điện và từ (ECG và MCG) dựa trên các mô hình nguồn có cùng số lượng biến độc lập, thì số bệnh nhân được chẩn đoán đúng là bằng nhau trong cả 2 phương pháp. Sự phân bố độ nhạy của các hệ thống đó càng chênh lệch thì sự sai khác về số lượng bệnh nhân được chẩn đoán đúng càng lớn. Vì chúng ta không biết bệnh nhân nào được chẩn đoán đúng với từng phương pháp nên chất lượng chẩn đoán tổng cộng không thể tăng lên bằng cách sử dụng riêng rẽ 2 phương pháp.

(B) Nếu quá trình chẩn đoán dựa trên sự kết hợp dữ liệu về cả mặt điện và từ (EMCG), số bệnh nhân được chẩn đoán đúng sẽ tăng lên, vùng được bao bởi cả 2 phương pháp.

20.7.5 Những kết luận tổng quát về phép đo từ tâm đồ

Dựa trên cơ sở lý thuyết về điện từ trường sinh học và những bài viết hiện nay trong lĩnh vực nghiên cứu MCG, chúng ta có thể đưa ra những kết luận tổng quát sau về ứng dụng của phép đo từ não đồ (Malmivuo, 1976):

1. MCG đo đặc tính hoạt động điện của cơ tim. Do đó, trên nền tảng về mặt giá cả, nếu chỉ sử dụng 1 trong 2 phương pháp trên khi các quá trình ghi dữ liệu mặt điện hoàn thành, ECG có thể được sử dụng, trừ khi có những nguyên nhân kĩ thuật phải chọn MCG (ví dụ, với những bệnh nhân bị bỏng da, ghi các trường DC...). 2. ECG đo trường điện thế, là một trường vô hướng. Do đó, một phép đo tại một điểm đo là đủ. MCG đo từ trường, là trường vector. Do đó, các phép đo MCG phải mô tả được 1 vector, cần 3 phép đo trực giao tại từng điểm đo để thu được toàn bộ thông tin có thể có (Malmivuo, 1976; Oostendorp, van Oosterom, và Huiskamp, 1992). 3. Trong MCG, chúng ta quan tâm đến hoạt động điện trong toàn bộ cơ tim chứ không chỉ ở trên bề mặt. Do đó, để bù lại hiệu ứng lân cận, các phép đo MCG cần thực hiện một cách đối xứng, ở cả đằng trước và đằng sau của ngực. Thật ra, phép đo MCG từ phía sau làm tăng lượng thông tin thu được ở phía sau của tim, mà ở đó độ nhạy của toàn bộ đạo trình ECG thấp do hiệu ứng cách ly của phổi. (Như đã chú ý trong các phần trước, trong phép đo MEG, chúng ta chủ yếu quan tâm đến hoạt động điện trên vỏ não. Do đó, phép đo đơn cực thích hợp trong việc đo MEG hơn.) 4. Trên cơ sở các bài viết hiện nay về MCG, phép đo đơn điểm không đối xứng có vẻ có cùng chất lượng chẩn đoán với phương pháp ánh xạ thành phần x của từ trường tại phần phía trước của ngực. 5. Sự kết hợp giữa các phép đo điện và từ (ví dụ, ECG và MCG) đưa tới chất lượng chẩn đoán tốt hơn từng phương pháp đo riêng rẽ với cùng số lượng thông số chẩn đoán, bởi vì số các phép đo độc lập tăng gấp đôi.

SÁCH THAM KHẢO

Baule GM, McFee R (1963): Detection of the magnetic field of the heart. Am. Heart J. 66:(7) 95-6. Baule GM, McFee R (1970): The magnetic heart vector. Am. Heart J. 79:(2) 223-36. Cohen D, Chandler L (1969): Measurements and simplified interpretation of magnetocardiograms from humans. Circulation 39: 395-402. Cohen D, Kaufman LA (1975): Magnetic determination of the relationship between the S-T segment shift and the injury current produced by coronary artery occlusion. Circ. Res. 36: 414. Cohen D, McCaughan D (1972): Magnetocardiograms and their variation over the chest in normal subjects. Am. J. Cardiol. 29:(5) 678-85. Cohen D, Norman JC, Molokhia F, Hood W (1971): Magnetocardiography of direct currents: S-T segment and baseline shifts during experimental myocardial infarction. Science 172:(6) 1329-33. Eskola H (1983): On the properties of vector magnetocardiographic leads. Tampere Univ. Tech., Tampere, Finland, Thesis, pp. 154. (Dr. tech. thesis) Eskola HJ, Malmivuo JA (1983): Optimizing vector magnetocardiographic lead fields by using physical torso model. Il Nuvo Cim. 2:(2) 356-67. Gulrajani RM, Savard P, Roberge FA (1988): The inverse problem in electrocardiography: Solution in terms of equivalent sources. CRC Crit. Rev. Biomed. Eng. 16: 171-214. Karp P (1981): Cardiomagnetism. In Biomagnetism, Proc. Third Internat. Workshop On Biomagnetism, Berlin (West), May 1980, ed. SN Erné, H-D Hahlbohm, H Lübbig, pp. 219-58, Walter de Gruyter, Berlin. Malmivuo JA (1976): On the detection of the magnetic heart vector - An application of the reciprocity theorem. Helsinki Univ. Tech., Acta Polytechn. Scand., El. Eng. Series. Vol. 39., pp. 112. (Dr. tech. thesis) Malmivuo JA (1980): Distribution of MEG detector sensitivity: An application of reciprocity. Med. & Biol. Eng. & Comput. 18:(3) 365-70. Malmivuo JA (1981): Properties of an ideal MCG-recording system. In Biomagnetism. Proc. Third Internat. Workshop On Biomagnetism, Berlin (West), May 1980, ed. SN Erné, H-D Hahlbohm, H Lübbig, pp. 343-9, Walter de Gruyter, Berlin. Malmivuo JA, Saarinen M, Siltanen P (1973): A clinical method in magnetocardiography. In Digest X Internat. Conf. Med. Biol. Eng, Vol. I, ed. A Albert, W Vogt, W Helbig, p. 251,, Dresden. Nenonen J, Katila T, Leiniö M, Montonen J, Mäkijärvi M, Siltanen P (1991): Magnetocardiographic functional localization using current multipole models. IEEE Trans. Biomed. Eng. 38:(7) 648-57. Nenonen J, Purcell CJ, Horácek BM, Stroink G, Katila T (1991): Magnetocardiographic functional localization using a current dipole in a realistic torso. IEEE Trans. Biomed. Eng. 38:(7) 658-64. Nousiainen JJ (1991): Behavior of the vector magnetocardiogram in normal subjects and in some abnormal cases. Tampere Univ. Tech., Tampere, Finland, Thesis, pp. 177. (Dr. tech. thesis) Nousiainen JJ, Lekkala JO, Malmivuo JA (1986): Comparative study of the normal vector magnetocardiogram and vector electrocardiogram. J. Electrocardiol. 19:(3) 275-90. Nousiainen J, Oja S, Malmivuo J (1994a): Normal vector magnetocardiogram. I. Correlation with the normal vector ECG. J. Electrocardiol. 27:(3) 221-231. Nousiainen J, Oja S, Malmivuo J (1994b): Normal vector magnetocardiogram. II. Effect of constitutional variables. J. Electrocardiol. 27:(3) 233-241. Oja OS (1993): Vector magnetocardiogram in myocardial disorders. University of Tampere, Medical Faculty, pp. 168. (MD thesis) Oostendorp TF, van Oosterom A, Huiskamp GJ (1992): The activation sequence of the heart as computed from all three magnetic field components. In Proc. Of the XIX International Congress On Electrocardiology, ., p. 132,, Lisbon. Rosen A, Inouye GT (1975): A study of the vector magnetocardiographic waveforms. IEEE Trans. Biomed. Eng. BME-22: 167-74. Rush S (1975): On the interdependence of magnetic and electric body surface recordings. IEEE Trans. Biomed. Eng. BME-22: 157-67. Saarinen M, Karp P, Katila T, Siltanen P (1978): The normal magnetocardiogram: I. Morphology. Ann. Clin. Res. 10:(S21) 1-43. Sakauchi Y, Kado H, Awano N, Kasai N, Higuchi M, Chinone K, Nakanishi M, Ohwada K, Kariyone M (1989): Measurement of cardiac magnetic field vector. In Advances in Biomagnetism, ed. SJ Williamson, M Hoke, G Stroink, M Kotani, pp. 425-8, Plenum Press, New York. Seppänen M, Katila T, Tuomisto T, Varpula T, Duret D, Karp P (1983): Measurement of the biomagnetic fields using multichannel superconducting magnetometer techniques. Il Nuvo Cim. 2 D: 166-74. Shirae K, Furukawa H, Katayama M (1988): Measurements and characteristics of vector magnetocardiography. In Biomagnetism '87, ed. K Atsumi, M Kotani, S Ueno, T Katila, SJ Williamson, pp. 294-7, Tokyo Denki University Press, Tokyo. Siltanen P (1989): Magnetocardiography. In Comprehensive Electrocardiology. Theory and Practice in Health and Disease, Vol. 2, ed. PW Macfarlane, TDV Lawrie, pp. 1405-38, Pergamon Press, New York. Stratton JA (1941): Electromagnetic Theory, McGraw-Hill, New York. Swithenby SJ (1987): Biomagnetism and the biomagnetic inverse problem. Phys. Med. Biol. MJ Day (ed.): The Biomagnetic Inverse Problem, 32:(1) 146. (Papers from a conference at the Open University, April 1986). Waller AD (1887): A demonstration on man of electromotive changes accompanying the heart's beat. J. Physiol. (Lond.) 8: 229-34. Wikswo JP, Malmivuo JA, Barry WM, Leifer M, Fairbank WM (1979): The theory and application of magnetocardiography. In Advances in Cardiovascular Physics, Vol. 2, ed. DN Ghista, pp. 1-67, S. Karger, Basel. Willems JL, Lesaffre E (1987): Comparison of multigroup logistic and linear discriminant ECG and VCG classification. J. Electrocardiol. 20: 83-92.

---

Trang trước

Từ tâm đồ

Trang tiếp

Liên kết đến đây

• Sách:Điện từ sinh học
• Sách:Điện từ sinh học/Cơ bản của điện tâm đồ chẩn đoán
• Sách:Điện từ sinh học/Kích thích điện từ của mô thần kinh