Toán học, Olympic toán toàn quốc - Việt nam 2001
A1. A circle center O meets a circle center O' at A and B. The line TT' touches the first circle at T and the second at T'. The perpendiculars from T and T' meet the line OO' at S and S'. The ray AS meets the first circle again at R, and the ray AS' meets the second circle again at R'. Show that R, B and R' are collinear.
A2.
Let
N
=
6n,
where
n
is
a
positive
integer,
and
let
M
=
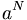 +
+
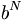 ,
where
a
and
b
are
relatively
prime
integers
greater
than
1.
M
has
at
least
two
odd
divisors
greater
than
1.
Find
the
residue
of
M
mod
6
,
where
a
and
b
are
relatively
prime
integers
greater
than
1.
M
has
at
least
two
odd
divisors
greater
than
1.
Find
the
residue
of
M
mod
6
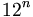 .
.
A3.
For
real
a,
b
define
the
sequence
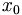 ,
,
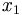 ,
,
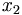 ,
...
by
,
...
by
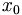 =
a,
=
a,
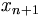 =
=
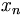 +
b
sin
+
b
sin
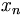 .
If
b
=
1,
show
that
the
sequence
converges
to
a
finite
limit
for
all
a.
If
b
>
2,
show
that
the
sequence
diverges
for
some
a.
.
If
b
=
1,
show
that
the
sequence
converges
to
a
finite
limit
for
all
a.
If
b
>
2,
show
that
the
sequence
diverges
for
some
a.
B1.
Find
the
maximum
value
of
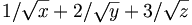 where
x,
y,
z
are
positive
reals
satisfying
where
x,
y,
z
are
positive
reals
satisfying
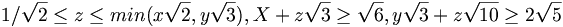 .
.
B2.
Find
all
real-valued
continuous
functions
defined
on
the
interval
(-1,
1)
such
that
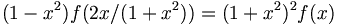 for
all
x.
for
all
x.
B3.
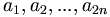 is
a
permutation
of
1,
2,
...
,
2n
such
that
is
a
permutation
of
1,
2,
...
,
2n
such
that
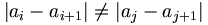 for
i
for
i
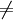 j.
Show
that
j.
Show
that
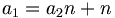 iff
1
iff
1
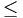
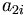
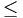 n
for
i
=
1,
2,
...
n.
n
for
i
=
1,
2,
...
n.


