Toán học, Tìm kiếm tài năng Toán Quốc tế, 2004 v1
Bài toán 1/1. Với mọi số nguyên dương n, lập số n/s(n), ở đó s(n) là tổng các chữ số của n trong hệ thập phân. Tính giá trị nhỏ nhất của n/s(n) trong mỗi trường hợp sau:
-
(i)
-
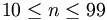
(ii)
-
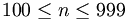
(iii)
-
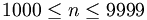
(iv)
.
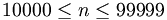Bài
toán
2/1.
Tìm
tất
cả
các
cặp
số
nguyên
(n,
k),
2
<
k
<
n,
sao
cho
các
số
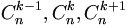tạo
thành
một
dãy
số
tăng.
Bài toán 3/1. Trên một bảng cỡ 8 x 8 người ta đặt n quân cờ Đôminô, mỗi quân chiếm hai ô kề nhau, sao cho không thể đặt thêm quân Đôminô nào vào các ô còn lại. Hỏi giá trị nhỏ nhất của n là bao nhiêu để trạng thái trên còn đúng?
Bài toán 4/1. Chứng minh rằng một tam giác nhọn tuỳ ý có thể bị cắt ra bởi các đoạn thẳng thành ba phần theo ba cách khác nhau sao cho mỗi phần có một trục đối xứng.
Bài toán 5/1. Chứng minh rằng có thể chia một tứ diện tuỳ ý thành 6 phần bởi các mặt phẳng hoặc phần mặt phẳng sao cho mỗi một phần có một mặt phẳng đối xứng.
