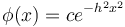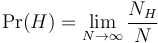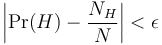Xác suất
 |
Bài
viết
hoặc
đoạn
này
cần
thêm
chú
thích
nguồn
gốc
để
có
thể
kiểm
chứng
thông
tin. Những nội dung không có nguồn có thể bị đặt vấn đề và xóa bỏ. Mời bạn bổ sung chú thích từ các nguồn đáng tin cậy để giúp cải thiện bài viết. |
Bản mẫu:Tính xác định Từ xác suất (probability) bắt nguồn từ chữ probare trong tiếng Latin và có nghĩa là "để chứng minh, để kiểm chứng". Nói một cách đơn giản, probable là một trong nhiều từ dùng để chỉ những sự kiện hoặc kiến thức chưa chắc chắn, và thường đi kèm với các từ như "có vẻ là", "mạo hiểm", "may rủi", "không chắc chắn" hay "nghi ngờ", tùy vào ngữ cảnh. "Cơ hội" (chance), "cá cược" (odds, bet) là những từ cho khái niệm tương tự. Nếu lí thuyết cơ học (cơ học cổ điển) có định nghĩa chính xác cho "công" và "lực", thì lí thuyết xác suất nhằm mục đích định nghĩa "khả năng".
Mục lục
Các giai đoạn lịch sử[sửa]
Khoa học nghiên cứu về xác suất là một phát triển trong thời kỳ cận đại. Việc chơi cờ bạc (gambling) cho chúng ta thấy rằng các ý niệm về xác suất đã có từ trước đây hàng nghìn năm, tuy nhiên các ý niệm đó được mô tả bởi toán học và sử dụng trong thực tế thì có muộn hơn rất nhiều.
Hai nhà toán học Pierre de Fermat và Blaise Pascal là những người đầu tiên đặt nền móng cho học thuyết về xác suất vào năm (1654). Christiaan Huygens (1657) được biết đến như là người đầu tiên có công trong việc đưa xác suất thành một vấn đề nghiên cứu khoa học.
Học thuyết chủ nghĩa về xác suất bắt đầu bằng những lần thư từ qua lại giữa Pierre de Fermat và Blaise Pascal (1654). Christiaan Huygens (1657) đã đưa ra những hiểu biết đầu tiên mang tính khoa học về vấn đề này. Các cuốn Ars Conjectandi của Jakob Bernoulli (sau khi chết, 1713) và Học thuyết chủ nghĩa cơ hội (Doctrine of Chances) của Abraham de Moivre (1718) đã xem xét chủ đề như một chi nhánh của ngành toán học.
Lý thuyết sai số (the theory of errors) có thể bắt đầu từ cuốn sách Opera Miscellanea của Roger Cotes (xuất bản sau khi ông mất, 1722), nhưng lí thuyết này đã được áp dụng lần đầu tiên trong một luận văn của Thomas Simpson vào năm 1755 (in vào năm 1756) trong thảo luận về sai số xảy ra trong quan sát (errors of observation). Bản in lại (1757) của luận văn này đưa ra tiên đề rằng khả năng sai số âm và dương (positive and negative errors) là ngang nhau, "và rằng có các giới hạn xác định được mà mọi sai số đều nằm trong các khoảng đó; các sai số liên tục được thảo luận và một đường cong xác suất được đưa ra" (and that there are certain assignable limits within which all errors may be supposed to fall; continuous errors are discussed and a probability curve is given).
Pierre-Simon
Laplace
(1774)
đã
thực
hiện
nỗ
lực
đầu
tiên
trong
việc
rút
ra
một
quy
luật
từ
việc
kết
hợp
các
quan
sát
từ
các
nguyên
lí
của
lí
thuyết
xác
suất.
Ông
đã
giới
thiệu
định
luật
xác
suất
về
sai
số
(the
law
of
probability
of
errors)
bằng
một
đường
cong
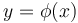 ,
,
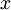 là
một
sai
số
bất
kì
và
là
một
sai
số
bất
kì
và
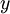 là
xác
suất
của
lỗi
đó,
và
đưa
ra
3
thuộc
tính
cho
đường
cong
này:
(1)
Nó
là
đối
xứng
qua
trục
là
xác
suất
của
lỗi
đó,
và
đưa
ra
3
thuộc
tính
cho
đường
cong
này:
(1)
Nó
là
đối
xứng
qua
trục
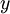 ;
(2)
trục
;
(2)
trục
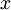 là
đường
tiệm
cận,
xác
suất
của
sai
số
là
đường
tiệm
cận,
xác
suất
của
sai
số
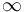 là
0;
(3)
diện
tích
vùng
bao
phủ
là
1,
thì
một
sai
số
là
tồn
tại.
Ông
cũng
đã
rút
ra
một
công
thức
từ
3
quan
sát
đó.
Ông
cũng
đã
đưa
ra
(1781)
một
công
thức
cho
định
luật
của
điều
kiện
của
sai
số
(the
law
of
facility
of
error)
(một
thuật
ngữ
của
Lagrange,
1774),
nhưng
công
thức
này
dẫn
đến
phương
trình
không
thể
giải
quyết
được.
Daniel
Bernoulli
(1778)
đã
giới
thiệu
nguyên
lí
của
tích
cực
đại
của
các
xác
suất
của
một
hệ
thống
sai
số
đồng
thời.
là
0;
(3)
diện
tích
vùng
bao
phủ
là
1,
thì
một
sai
số
là
tồn
tại.
Ông
cũng
đã
rút
ra
một
công
thức
từ
3
quan
sát
đó.
Ông
cũng
đã
đưa
ra
(1781)
một
công
thức
cho
định
luật
của
điều
kiện
của
sai
số
(the
law
of
facility
of
error)
(một
thuật
ngữ
của
Lagrange,
1774),
nhưng
công
thức
này
dẫn
đến
phương
trình
không
thể
giải
quyết
được.
Daniel
Bernoulli
(1778)
đã
giới
thiệu
nguyên
lí
của
tích
cực
đại
của
các
xác
suất
của
một
hệ
thống
sai
số
đồng
thời.
Phương pháp bình phương cực tiểu do Adrien-Marie Legendre (1805), giới thiệu trong cuốn Nouvelles méthodes pour la détermination des orbites des comètes (Những Phương pháp mới để Xác định Quỹ đạo Sao chổi). Không biết đến đóng góp của Legendre, Robert Adrain, một tác giả Mỹ gốc Ireland, chủ bút tạp chí The Analyst (1808), lần đầu đưa ra định luật điều kiện của sai số,
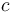 và
và
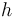 là
các
hằng
số
phụ
thuộc
vào
độ
chính
xác
của
quan
sát.
là
các
hằng
số
phụ
thuộc
vào
độ
chính
xác
của
quan
sát.
Ông
đưa
ra
hai
chứng
minh,
chứng
minh
thứ
hai
về
cơ
bản
giống
với
chứng
minh
của
John
Herschel
(1850).
Carl
Friedrich
Gauss
đưa
ra
chứng
minh
thứ
nhất,
dù
chứng
minh
này
có
thể
đã
được
biết
đến
ở
châu
Âu
là
chứng
minh
thứ
ba
sau
Adrain,
vào
năm
1809.
Các
chứng
minh
tiếp
theo
đã
được
Laplace
(1810,
1812),
Gauss
(1823),
James
Ivory
(1825,
1826),
Hagen
(1837),
Friedrich
Bessel
(1838),
Donkin
(1844,
1856)
và
Morgan
Crofton
(1870)
đưa
ra.
Các
tác
giả
khác
đã
đóng
góp
vào
định
luật
này
là
Ellis
(1844),
Augustus
De
Morgan
(1864),
Glaisher
(1872)
và
Giovanni
Schiaparelli
(1875).
Công
thức
của
Peters
(1856)
về
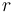 ,
sai
số
xác
suất
của
một
quan
sát,
rất
phổ
biến.
,
sai
số
xác
suất
của
một
quan
sát,
rất
phổ
biến.
Vào thế kỷ 19 các tác giả về lý thuyết xác suất có Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion và Karl Pearson. Augustus De Morgan và George Boole đã đóng góp vào việc giải thích lý thuyết xác suất.
Về mặt hình học (xem hình học giải tích) các tác giả có ảnh hưởng lớn là Miller, Crofton, McColl, Wolstenholme, Watson và Artemas Martin.
Khái niệm[sửa]
Về cơ bản có một tập hợp những quy luật toán để có thể biến đổi các giá trị của xác suất; những quy luật nầy sẽ được liệt kê ra trong phần "Sự hình thành của xác suất" dưới đâỵ. (Có một số các quy luật được khác dùng để định lượng sự ngẫu nhiên như trong lý thuyết Dempster-Shafer và lý thuyết khả tạo nhưng những quy luật này thì khác biệt từ bản chất và không tương hợp với cách hiểu thông thường các định luật về xác suất. Tuy nhiên, người ta vẫn còn tranh biện về những đối tượng chính xác nào mà trên đó những quy luật này được áp dụng. Đây là đầu đề của những diễn dịch của xác suất.
Ý tưởng chung của xác suất thường được chia thành 2 khái niệm liên quan:
- Xác suất may rủi (aleatory probability), đề cập đến khả năng xảy ra của các sự kiện trong tương lai mà khả năng xảy ra của các sự kiện này phụ thuộc vào một hiện tượng vật lí nào đó mang tính ngẫu nhiên. Khái niệm này còn được chia ra thành (1) các hiện tượng vật lí, về cơ bản, có thể dự đoán được khi có đủ thông tin và (2) các hiện tượng không thể dự đoán được. Ví dụ của loại trước là việc thả một con súc sắc hay quay một bánh xe roulette; ví dụ của loại sau là sự phân rã hạt nhân.
- Xác suất trong tri thức (epistemic probability), đề cập đến sự không chắc chắn của chúng ta về một mệnh đề nào đó vì thiếu thông tin cung cấp để suy luận. Ví dụ việc xác định khả năng một nghi phạm là có phạm tội, dựa trên các chứng cứ cung cấp.
Sự hình thành xác suất[sửa]
Như các lý thuyết khác, lý thuyết xác suất là một biểu diễn của khái niệm xác suất bằng các thuật ngữ hình thức - nghĩa là các thuật ngữ mà có thể xác định một cách độc lập với ý nghĩa của nó. Các thuật ngữ hình thức này được thao tác bởi các quy luật toán học và logic, và kết quả thu được sẽ được chuyển dịch trở lại miền (domain) của bài toán.
Có hai hướng công thức hóa xác suất đã thành công là sự hình thành công thức Kolmogorov và sự hình thành công thức Cox. Trong công thức của Kolmogorov, các tập được hiểu là các sự kiện và xác suất chính là một phép đo trên một lớp các tập đó.
Trong công thức của Cox, xác suất được xem là cái cơ bản (primitive - không thể phân tích thêm được nữa) và tập trung nghiên cứu vào việc xây dựng một phép gán tốt các giá trị xác suất đến các mệnh đề. Trong cả 2 trường hợp, các định luật về xác suất là như nhau, ngoại trừ yếu tố chi tiết kĩ thuật:
- xác suất là một giá trị số trong khoảng 0 và 1;
- xác suất của một sự kiện hay mệnh đề và phần bù của nó cộng lại phải bằng 1; và
- xác suất kết hợp của hai sự kiện hay hai mệnh đề là tích của các xác suất của một trong chúng và xác suất của cái thứ hai với điều kiện biết cái trước xảy ra.
Cách biểu diễn và chuyển đổi các giá trị xác suất[sửa]
Xác suất của một sự kiện thương được biểu diễn bằng số thực trong khoảng 0 và 1, bao gồm 2 giá trị biên. Và một sự kiện không thể xảy ra thì có xác suất là 0, còn một sự kiện chắc chắn thì có xác suất là 1, nhưng điều ngược lại không đúng. Sự khác biệt giữa "chắc chắn" và "xác suất xảy ra 1" là rất quan trọng.
Hầu hết các giá trị xác suất xảy ra trong thực tế là giữa 0 và 1.
Sự phân bố[sửa]
Một phân bố xác suất là một hàm số nhằm gán các giá trị (gọi là xác suất) cho các sự kiện. Các giá trị số này đặc trưng cho khả năng xảy ra của các sự kiện. Với một tập bất kì các sự kiện, có rất nhiều cách để gán các xác suất, và thường dựa vào sự lựa chọn loại phân bố của các sự kiện đang xem xét.
Có nhiều cách để chỉ định một phân bố xác suất. Thông thường nhất có lẽ là chỉ định một hàm mật độ xác suất (probability density function). Từ đó, xác suất của một sự kiện sẽ được bằng cách lấy tích phân hàm mật độ. Tuy nhiên, hàm phân bố cũng có thể được chỉ định rõ trực tiếp. Trong trường hợp chỉ có một biến (hay một chiều), thì hàm phân bố được gọi là hàm phân bố tích lũy (cumulative distribution function). Phân bố xác suất cũng có thể được chỉ định thông qua các giá trị mômen hay hàm đặc trưng (characteristic function), hay các cách khác nữa.
Một phân bố được gọi là phân bố rời rạc nếu nó được định ra trên một tập rời rạc, đếm được; ví dụ tập các số nguyên.
Một phân bố được gọi là phân bố liên tục nếu nó được định ra trên một tập vô hạn, không đếm được.
Hầu hết các phân bố trong các ứng dụng thực tế đều hoặc là một trong hai, nhưng có một số ví dụ về phân bố bao gồm của cả 2, gọi là phân bố hỗn hợp.
Các phân bố rời rạc quan trọng bao gồm phân bố đồng nhất, phân bố Poisson, phân bố nhị thức, phân bố nhị thức âm và phân bố Maxwell-Boltzmann.
Các phân bố liên tục quan trọng bao gồm phân bố chuẩn (hay còn gọi là phân bố Gauss), phân bố gamma, phân bố-t của Student (Student's t-distribution), và phân bố hàm mũ (exponential distribution).
Xác suất với toán học[sửa]
Tiên đề xác suất tạo thành nền tảng cho lý thuyết xác suất. Việc tính toán các xác suất thường dựa vào phép tổ hợp hoặc áp dụng trực tiếp các tiên đề. Các ứng dụng xác suất bao gồm thống kê, nó dựa vào ý tưởng phân bố xác suất và định lý giới hạn trung tâm.
Để minh họa, ta xem việc tung một đồng xu cân đối. Về mặt trực quan, xác suất để head xuất hiện phía trên là 50%; nhưng phát biểu này thiếu tính toán học - Vậy con số 50% có ý nghĩa thực sự thế nào trong ví dụ này?
Một hướng là dùng định luật số lớn. Giả sử là ta thực hiện một số lần gieo đồng xu, với mỗi lần gieo là độc lập nhau - nghĩa là, kết quả của 2 lần gieo khác nhau là độc lập nhau. Nếu ta tiến hành N lần gieo (trials), và đặt NH là số lần mà mặt head xuất hiện, thì với tỉ lệ NH/N.
Khi số lần gieo N trở nên lớn, ta kì vọng rằng tỉ lệ NH/N sẽ tiến gần hơn đến giá trị 1/2. Điều này cho phép ta định nghĩa xác suất Pr(H) của mặt head xuất hiện là giới hạn, khi N tiến ra vô cùng, của chuỗi các tỉ lệ này:
Trong thực tế, dĩ nhiên ta không thể tiến hành vô hạn lần các lần gieo được; vì thế, nói chung công thức này áp dụng chính xác cho tình huống khi mà chúng ta biết được một xác suất cho sắn (a priori) cho một kết quả đầu ra nào đó (mà trong ví dụ này là thông tin đồng xu cân đối). Khi đó, định luật số lớn phát biểu rằng, khi cho biết Pr(H), và với một số nhỏ bất kì ε, luôn tồn tại một giá trị n sao cho với mọi N > n,
Khía cạnh thông tin cho sẵn a priori của hướng tiếp cận này đôi khi gặp khó khăn trong thực tiễn. Ví dụ, trong với kịch Rosencrantz and Guildenstern are Dead của Tom Stoppard, một nhân vật gieo đồng xu mà luôn xuất hiện mặt head, sau 100 lần gieo. Ông ta không thể xác định đây là sự kiện ngẫu nhiên hay không - vì dù sao, điều này vẫn có thể xảy ra với đồng xu cân đối (dù hiếm).
Những chú ý khi tính toán xác suất[sửa]
Khó khăn trong việc tính toán xác suất nằm ở việc xác định số sự kiện có thể xảy ra (possible events): đếm số lần xuất hiện của mỗi sự kiện, và đếm số lượng sự kiện có thể xảy ra đó. Đặc biệt khó khăn trong việc rút ra một kết luận có ý nghĩa từ các xác suất tính được. Một bài toán đố thú vị, bài toán Monty Hall sẽ cho thấy điều này.
Để học thêm về cơ bản của lí thuyết xác suất, xem bài viết về tiên đề xác suất và định lý Bayes giải thích việc sử dụng xác suất có điều kiện trong trường hợp sự xuất hiện của 2 sự kiện là có liên quan nhau.
Ứng dụng của xác suất với đời sống hàng ngày[sửa]
Ảnh hưởng chính của lý thuyết xác suất trong cuộc sống hằng ngày đó là việc xác định rủi ro và trong buôn bán hàng hóa. Chính phủ cũng áp dụng các phương pháp xác suất để điều tiết môi trường hay còn gọi là phân tích đường lối.
Lý thuyết trò chơi cũng dựa trên nền tảng xác suất. Một ứng dụng khác là trong xác định độ tin cậy. Nhiều sản phẩm tiêu dùng như xe hơi, đồ điện tử sử dụng lý thuyết độ tin cậy trong thiết kế sản phẩm để giảm thiểu xác suất hỏng hóc. Xác suất hư hỏng cũng gắn liền với sự bảo hành của sản phẩm.
Các câu nói nổi tiếng về xác suất[sửa]
- Damon Runyon: "It may be that the race is not always to the swift, nor the battle to the strong - but that is the way to bet."
- Pierre-Simon Laplace: "It is remarkable that a science which began with the consideration of games of chance should have become the most important object of human knowledge." Théorie Analytique des Probabilités, 1812.
- Richard von Mises: "The unlimited extension of the validity of the exact sciences was a characteristic feature of the exaggerated rationalism of the eighteenth century" (Probability, Statistics, and Truth, tr. 9. Ấn bản Dover, 1981 (tái bản ấn bản 2 bằng tiếng Anh, 1957).
- Richard von Mises: "LIE" (Probability, Statistics, and Truth, tr. 9. Ấn bản Dover, 1981 (tái bản ấn bản 2 bằng tiếng Anh, 1957).
Xem thêm[sửa]
- Xác suất Bayes
- Quá trình Bernoulli
- Định lí Cox
- Lý thuyết quyết định
- Lý thuyết phép đo mờ
- Trò chơi may rủi
- Lý thuyết trò chơi
- Lý thuyết thông tin
- Định luật trung bình
- Định luật số lớn
- Lý thuyết phép đo
- Phân phối chuẩn
- Trường ngẫu nhiên
- Biến ngẫu nhiên
- Thống kê
- Quá trình ngẫu nhiên
- Quá trình Wiener
Tham khảo[sửa]
Liên kết ngoài[sửa]
- A Collection of articles on Probability, many of which are accompanied by Java simulations
- Edwin Thompson Jaynes. Probability Theory: The Logic of Science. Preprint: Washington University, (1996). -- HTML and PDF
- An online probability textbook which uses computer programming as a teaching aid
- Probabilistic football prediction competition, probabilistic scoring and Đọc thêm.
- "The Not So Random Coin Toss, Mathematicians Say Slight but Real Bias Toward Heads". NPR.
- Poker Probability
- Figuring the Odds (Probability Puzzles)
- Probability and Poker
- Dictionary of the History of Ideas: Certainty in Seventeenth-Century Thought
- Dictionary of the History of Ideas: Certainty since the Seventeenth Century